Skip to main content
SpringerLink
Log in

The Most Unstable Profiles of a Plane-Parallel Flow in a Channel

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

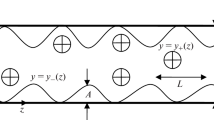
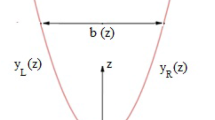
It is well known (after Rayleigh) that a plan-parallel flow in a channel can be unstable only if the basic velocity profile U(z) possesses inflection points. The profile determines (via the Rayleigh equation) the maximal increment ∣αc i∣ of small perturbations and 'eigenvalues' c (see Equation (1)). The increment and the imaginary parts c i of the eigenvalues c provide a quantitative characterization of the basic stability properties of the flow. Here we find some best possible bounds for these values. The bounds are determined by the following parameters: wave number α; enstrophy \(1/2\int_0^L {[U'(z)]^2 } {\text{d}}z\) of the basic flow; width of the channel L. A similar approach can be applied to models of atmosphere, ocean, plasma etc.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Arakawa, A., 'Computational design for long-term numerical integration of the equations of fluid motions: two-dimensional incompressible flow, Part I', J. Comp. Phys. 1(1) (1966) 119-143.

    Google Scholar 

  2. Arnold, V.I., Mathematical Methods of Classical Mechanics, 2nd ed. Nauka, Moscow, (Russian), Springer-Verlag, Berlin, 1989.

    Google Scholar 

  3. Dickey, L.A., The Hydrodynamical Stability and Dynamics of the Atmosphere, Gidrometeoizdat, 1976 (in Russian).

  4. Diedrichs, B., 'Three-dimensional disturbances; considering starting profiles and optimal profiles in Couette and Poiseuille flow', Phys. Fluid 8(5) (1996) 1149-1158.

    Google Scholar 

  5. Drazin, P.G. and Howard, L.N., 'Hydrodynamic stability of parallel flow of inviscid fluid', In: G.G. Chernyi et al. (eds) Advances Appl. Mech. 9 1966.

  6. Drazin, P.G. and Reid, W.H., Hydrodynamic Stability, Cambridge Univ. Press, 1981.

  7. Faddeev, D.K. and Faddeeva, V.N., 'About natural norms for estimation of the solution of a finite computational problem', J. Numer. Math. & Math. Phys. 9(1) (1969) 3-13 (in Russian).

    Google Scholar 

  8. Fedorenko, R.P., Introduction into Computational Physics, MPTI, Moscow, 1994 (in Russian).

    Google Scholar 

  9. Gordin, V.A. and Petviashvili, V.I., 'The class of the steady soliton solution in resonance zonal flow', Izvestia of USSR Academy of Sciences. Series “The Physics of Atmosphere and Ocean” 20(7) (1984) 645-648 (in Russian), 583-585 (in English).

    Google Scholar 

  10. Gordin, V.A., Mathematical Problems of the Hydrodynamical Weather Forecast. Analytical aspects, Vol. 1; Computational aspects, Vol. 2, Gidrometeoizdat, Leningrad, 1987 (in Russian), Gordon & Breach Science Publishers, 2000.

    Google Scholar 

  11. Gordin, V.A. and Petviashvili, V.I., 'The sufficient condition for the stability of cylindrical plasma', Plasma Phys. 51(7) (1989) 240-246 (in Russian); Sov. J. Plasma Phys. 140-141 (in English).

    Google Scholar 

  12. Gordin, V.A. and Petviashvili V.I., 'Lyapunov stability of MHD equilibrium of a plasma with nonvanishing pressure', JETP 68(5) (1989) 1711-1722 (in Russian); 988-994 (in English).

    Google Scholar 

  13. Gordin, V.A., 'Optimization of eigenvalue of the Shrödinger equation with respect to potential', Russian Theoretical & Mathematical Physics 5(4) (1997) 521-526.

    Google Scholar 

  14. Gordin, V.A., 'First integrals of evolution systems and non-linear stability of stationary solutions for the ideal atmospheric, oceanic, hydrodynamical and plasma models', Proc. Int. Conf. Nonlinear Dynamics, Chaotic and Complex Systems, 1995, Zakopane, J. Tech. Physics 39(2) (1998) 213-219.

    Google Scholar 

  15. Howard, L.N., 'Note on a paper of John W. Miles', J. Fluid Mech. 10(4) (1961) 509-512.

    Google Scholar 

  16. Joseph, D.D., Stability of Fluid Motions, Springer-Verlag, 1976.

  17. Kalyagin, V.A. and Stepanyants, Yu. A., Lyapunov-ArnoldMethod in the Hydrodynamic Theory of Stability. Inst. Applied Physics, Nizhny Novgorod, (in Russian) 1995.

    Google Scholar 

  18. Kelvin, W. and Thomson, Baron., 'On a disturbing infinity of Lord Rayleigh's solution for waves in a plane vortex stratum', Nature 23 (1880) 45-46.

    Google Scholar 

  19. Kelvin, W. and Thomson, Baron., 'On the stability of steady and of periodic fluid motion', Phil. Mag. 23 (1887) 529-539.

    Google Scholar 

  20. Kozyrev, O.R. and Stepanyants, Yu. A., 'The integral relation method in the linear theory of hydrodynamic stability', In: Advances in Science and Technology, Ser. Mechanics of Fluids and Gases, Vol. 25, VINITI, Moscow (in Russian) (1991) pp. 3-89.

    Google Scholar 

  21. Miles, J.W., 'On the stability of heterogeneous shear flows', J. Fluid Mech. 10(4) (1961) 496-508.

    Google Scholar 

  22. Rayleigh, J.W., The Theory of Sound, Dover, 1945.

  23. Young, W.R., 'Selective decay of enstrophy and the excitation of barotropic waves in a channel', J. Atm. Sci. 44(19) (1987) 2804-2812.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Hydrometeorological Center of Russia, Bolshoi Predtechenskii, per., 9-13, 123376, Russia, Moscow

    Vladimir A. Gordin

Authors
  1. Vladimir A. Gordin
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gordin, V.A. The Most Unstable Profiles of a Plane-Parallel Flow in a Channel. Meccanica 35, 39–53 (2000). https://doi.org/10.1023/A:1004842312649

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1004842312649

Search

Navigation