Skip to main content
SpringerLink
Log in

Optimal discharging in a branched estuary

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

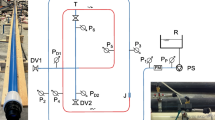
For wastewater discharged into one branch of a narrow estuary, the resulting maximum concentration or temperature can vary markedly depending upon the proximity of the discharge site to the branching and upon how the rate of discharge is adjusted. Explicit formulae are derived for the optimal discharge rate to minimize the maximum concentration or temperature experienced in the estuary, while disposing of a given total wasteload over a tidal period. Graphs are used to show the approximately factors of two reductions in that minimized maximum concentration or temperature when the second branch is large, the discharge close to the branching, the decay rate large or the mean river flow large. By optimizing with respect to one pollutant, there is a reasonably wide range of other pollutants for which the environmental impact is nearly minimized.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T. Webb and R.B. Tomlinson, Design procedures for effluent discharge to estuaries during ebb tide. J. Env. Eng. ASCE 118 (1992) 338-362.

    Google Scholar 

  2. R. Smith, Optimum use of holding tanks to avoid pollution surges in narrow estuaries. IMA J. Appl. Math. 51 (1993) 187-499.

    Google Scholar 

  3. R.T. Giles, Optimal strategies for discharging pollutants into narrow estuaries. Water Research 29 (1995) 563-569.

    Google Scholar 

  4. J.H. Bikangaga and V. Nassehi, Application of computer modelling techniques to the determination of optimum effluent discharge policies in tidal water systems. Water Research 29 (1995) 2367-2375.

    Google Scholar 

  5. R. Smith and A Purnama, Two outfalls in an estuary: Optimal wasteload allocation. J. Eng. Math. 35 (1999) 273-283.

    Google Scholar 

  6. A. Kay, Advection-diffusion in reversing and oscillating flows: 1. The effect of a single reversal. IMA J. Appl. Math. 45 (1990) 115-1437.

    Google Scholar 

  7. E.R. Holley Difference modelling of stream pollution. J. Sanit. Eng. ASCE 100 (1969) 968-972.

    Google Scholar 

  8. W.H. Li and M.E. Kozlowski, DO-sag in oscillatory flow. J. Env. Eng. ASCE 100 (1974) 837-854.

    Google Scholar 

  9. G.J. Macdonald, and R.N. Weisman, Oxygen-sag in a tidal river. J. Env. Eng. ASCE 103 (1977) 473-488.

    Google Scholar 

  10. D.J. O'Connor, Estuarine distribution of nonconservative substances. J. Sanit. Eng. ASCE 91 (1965) 23-42.

    Google Scholar 

  11. J.B. Schijf and J.C. Schonfeld, Theoretical considerations on the motion of salt and fresh water. Proc. Minn. Int. Hydraul. Conference, Minneapolis, Minn. (1953) 321-333.

  12. J.M. Gaudet and A.G. Roij, Effect of bed morphology on flow mixing length at river confluences. Nature 373 (1995) 138-139.

    Google Scholar 

  13. A. Kay, Advection-diffusion in reversing and oscillating flows: 2. Flows with multiple reversals. IMA J. Appl. Math. 58 (1990) 185-210.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Loughborough University, LE11 3TU, U.K.

    R. Smith

Authors
  1. R. Smith
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Smith, R. Optimal discharging in a branched estuary. Journal of Engineering Mathematics 38, 309–322 (2000). https://doi.org/10.1023/A:1004747216103

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1004747216103

Search

Navigation