Skip to main content
SpringerLink
Log in

Higher-order triangular and tetrahedral finite elements with mass lumping for solving the wave equation

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

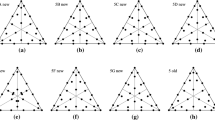
The higher-order finite-element scheme with mass lumping for triangles and tetrahedra is an efficient method for solving the wave equation. A number of lower-order elements have already been found. Here the search for elements of higher order is continued. Elements are constructed in a systematic manner. The nodes are chosen in a symmetric way. Integration rules must be exact up to a certain degree to maintain an overall accuracy that is the same as without mass lumping. First, for given integration degrees, consistent rule structures are derived for which integration formulas are likely to exist. Then, as each rule structure corresponds to a potential element of certain order, the position of element nodes and the integration weights can be found by solving the related system of nonlinear equations. With this systematic approach, a number of new sixth-order triangular elements and a new fourth-order tetrahedral element have been found.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Fried and D. S. Malkus, Finite element mass matrix lumping by numerical integration without convergence rate loss. Int. J. Solids Struc. 11 (1976) 461-466.

    Google Scholar 

  2. G. Cohen, P. Jody and N. Tordjman, Construction and analysis of higher order finite elements with mass lumping for the wave equation. In: R. Kleinman, T. Angell, D. Colton, F. Santosa and I. Stakgold (eds), Proc. of the 2nd International Conference on Mathematical and Numerical Aspects of Wave Propagation. Philadelphia: SIAM (1993) pp. 152-160.

    Google Scholar 

  3. G. Cohen, P. Joly and N. Tordjman, Higher order triangular finite elements with mass lumping for the wave equation. In: G. Cohen, E. Bécache, P. Joly and J. E. Roberts (eds), Proc. of the 3rd International Conference on Mathematical and Numerical Aspects of Wave Propagation. Philadelphia: SIAM (1995) pp. 270-279.

    Google Scholar 

  4. N. Tordjman, Élements finis d'order élevé avec condensation de masse pour l'equation des ondes. Ph.D. dissertation, L'Université Paris IX Dauphine (1995) 300 pp.

  5. W. A. Mulder, A comparison between higher-order finite elements and finite differences for solving the wave equation, In: J.-A. Désidéri, P. Le Tallec, E. Oñate, J. Périaux and E. Stein (eds), Proceedings of the Second ECCOMAS Conference on Numerical Methods in Engineering (Paris, Sept. 9–13, 1996), John Wiley and Sons (1996) pp. 344-350.

  6. W. A. Mulder, Spurious modes in finite-element discretisations of the wave equation may not be all that bad. Submitted to Appl. Num. Math.

  7. P. Keast and J. C. Diaz, Fully symmetric integration formulas for the surface of the sphere in s dimensions. SIAM J. Num. Anal. 20 (1983) 406-419.

    Google Scholar 

  8. P. Keast, Moderate-degree tetrahedral quadrature formulas. Comp. Meth. Appl. Mech. Eng. 55 (1986) 339-348.

    Google Scholar 

  9. P. Keast, Cubature formulas for the surface of the sphere. J. Comp. Appl. Math. 17 (1987) 151-172.

    Google Scholar 

  10. M. A. Dablain, The application of higher-order differencing to the scalar wave equation. Geophysics 51 (1986) 54-66.

    Google Scholar 

  11. J. I. Maeztu and E. Sainz de la Maza, Consistent structures of invariant quadrature rules for the n-Simplex. Math. Comp. 64 (1995) 1171-1192.

    Google Scholar 

  12. P. G. Ciarlet and J. L. Lions, Handbook of Numerical Analysis. Vol. II: Finite Element Methods. (Part 1). Amsterdam: North-Holland (1989) 928 pp.

    Google Scholar 

  13. G. Strang and G. J. Fix, An Analysis of the Finite Element Method. Englewood Cliffs, N.J.: Prentice Hall (1973) 306 pp.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Computer Sciences, Vrije Universiteit, Amsterdam, The Netherlands; e-mail

    M. J. S. Chin-Joe-Kong & M. Van Veldhuizen

  2. Shell International Exploration and Production B.V., Postbus 60, 2280 AB, Rijswijk, The Netherlands

    W. A. Mulder

Authors
  1. M. J. S. Chin-Joe-Kong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. W. A. Mulder
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Van Veldhuizen
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chin-Joe-Kong, M.J.S., Mulder, W.A. & Van Veldhuizen, M. Higher-order triangular and tetrahedral finite elements with mass lumping for solving the wave equation. Journal of Engineering Mathematics 35, 405–426 (1999). https://doi.org/10.1023/A:1004420829610

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1004420829610

Search

Navigation