Abstract
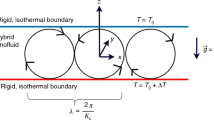
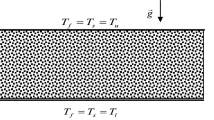
We consider the solidification of a binary alloy in a mushy layer subject to Coriolis effects. A near-eutectic approximation and large far-field temperature is employed in order to study the dynamics of the mushy layer with a Stefan number of unit order of magnitude. The weak nonlinear theory is used to investigate analytically the Coriolis effect in a rotating mushy layer for a new moderate time scale proposed by the author. It is found that increasing the Taylor number favoured the forward bifurcation.
Similar content being viewed by others
References
Amberg, G. and Homsey, G. M.: 1993, Nonlinear analysis of buoyant convection in binary solidification to channel formation, J. Fluid Mech. 252, 79–98.
Anderson, D. M. and Worster, M. G.: 1995, Weakly nonlinear analysis of convection in mushy layers during the solidification of binary alloys, J. Fluid Mech. 302, 307–331.
Anderson, D. M. and Worster, M. G.: 1996, A new oscillatory instability in a mushy layer during the solidification of binary alloys, J. Fluid Mech. 307, 245–267.
Chen, F., Lu, J. W. and Yang, T. L.: 1994, Convective instability in ammonium chloride solution directionally solidified from below, J. Fluid Mech. 276, 163–187.
Copley, S. M., Giamei, A. F., Johnson, S. M. and Hornbecker, M. F.: 1970, The origin of freckles in unidirectionally solidified castings, Metall. Trans. 1, 2193–2205.
Drazin, P. G. and Reid, W. H.: 1981, Hydrodynamic Stability, Cambridge University Press.
Fowler, A. C.: 1985, The formation of freckles in binary alloys, IMA J. App. Math. 35, 159–174.
Newell, A. C. and Whitehead, J. C.: 1969, Finite bandwidth, finite amplitude convection, J. Fluid. Mech. 38, 297–303.
Nield, D. A.: 1999, Modelling effects of a magnetic field or rotation on flow in a porous medium, Int. J. Heat and Mass Tran. 42, 3715–3718.
Segel, L. A.: 1969, Distant side-walls cause slow amplitude modulation of cellular convection, J. Fluid. Mech. 38, 203–224.
Vadasz, P.: 1998, Coriolis effect on gravity driven convection in a rotating porous layer heated from below, J. Fluid. Mech. 376, 351–375.
Worster, M. G.: 1992, Instabilities of the liquid and mushy regions during solidification of alloys, J. Fluid. Mech. 237, 649–669.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Govender, S., Vadasz, P. Weak Nonlinear Analysis of Moderate Stefan Number Oscillatory Convection in Rotating Mushy Layers. Transport in Porous Media 48, 353–372 (2002). https://doi.org/10.1023/A:1015755420045
Issue Date:
DOI: https://doi.org/10.1023/A:1015755420045