Abstract
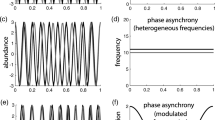
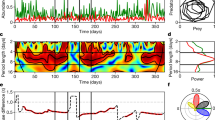
The apparent synchronisation of spatially discrete populations is a well documented phenomenon. However, it is not clear what the governing mechanisms are for this synchrony, and whether they are robust over a range of environmental conditions and patch specific population dynamic behaviours. In this paper, we explore two (possibly interacting) modes of coupling, and investigate their theoretically discernible, and perhaps even experimentally measurable, signatures. To aid us in this investigation we employ a planktonic example system, with direct application to plankton patchiness. Furthermore, we address the role of chaos in complex spatio-temporal dynamics; we find that chaos associated with funnel attractors can play a distinguished role, over dynamics less sensitive to small variations, in being more susceptible to generalised synchronisation (such as phase synchronisation) in the presence of small local parameter variation. This is in contrast to the case for coupled systems with identical dynamics, and suggests that non-identically coupled systems are more vulnerable to global extinction events when exhibiting funnel-type chaotic dynamics.
Similar content being viewed by others
References
Abarbanel, H. D. I., N. F. Rulkov and M. M. Sushchik (1996). Generalized synchronization of chaos: the auxiliary systems approach. Phys. Rev. E 53, 4258–4535.
Alexander, J. C., J. A. Yorke, Z. You and I. Kan (1992). Riddled basins. Int. J. Bifurcation Chaos 2, 795–813.
Allen, J., W. Schaffer and D. Rosko (1993). Chaos reduces species extinction by amplifying local population noise. Nature 364, 229–234.
Ashwin, P., J. Buescu and I. Stewart (1994). Bubbling of attractors and synchronisation of chaotic oscillators. Phys. Lett. A 193, 126–139.
Belykh, B., I. V. Belykh and E. Mosekilde (2001). Cluster synchronization modes in an ensemble of coupled chaotic oscillators. Phys. Rev. E 63, 036216.
Blasius, B. and L. Stone (2000a). Chaos and phase synchronization in ecological systems. Int. J. Bifurcation Chaos 10, 2361–2380.
Blasius, B. and L. Stone (2000b). Nonlinearity and the Moran effect. Nature 406, 846–847.
Dunn, M. R. and M. G. Pawson (2002). The stock structure and migrations of plaice populations on the west coast of England and Wales. J. Fish Biol. 61, 360–393.
Eckmann, J.-P. and D. Ruelle (1985). Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57, 617–656.
Edwards, A. M. and M. A. Bees (2001). Generic dynamics of a simple plankton population model with a non-integer exponent of closure. Chaos Solitons Fractals 12, 289–300.
Edwards, A. M. and J. Brindley (1996). Oscillatory behaviour in a three component plankton population model. Dyn. Stab. Syst. 11, 347–370.
Fox, C. J., B. P. Planque and C. P. Darby (2002). Synchrony in the recruitment time-series of plaice (Pleuronectes platessa L) around the United Kingdom and the influence of sea temperature. J. Sea. Res. 44, 159–168.
Fujisaka, H. and T. Yamada (1983). Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 69, 32–48.
Grenfell, B. T., K. Wilson, B. F. Finkelstädt, T. N. Coulson, S. Murray, S. D. Albon, J. M. Pemberton, T. H. Clutton-Brock and M. J. Crawley (1998). Noise and determinism in synchronized sheep dynamics. Nature 394, 674–677.
Hastings, A. and T. Powell (1991). Chaos in a three species food chain. Ecology 72, 896–903.
Hillary, R. M. (2003). Effects of turbulence and a patchy environment on the dynamics of plankton populations, PhD thesis, University of Surrey.
Hillary, R. M. and M. A. Bees (2004). Plankton lattices and the role of chaos in plankton patchiness. Phys. Rev. E 69, 031913.
Hudson, P. J. and I. M. Cattadori (1999). The Moran effect: a cause of population synchrony. TREE 14, 1–2.
Josic, K. (1998). Invariant manifolds and synchronization of coupled dynamical systems. Phys. Rev. Lett. 80, 3053–3056.
Keith, L. B. (1963). Wildlife’s Ten Year Cycle, Cambridge: Cambridge University Press.
Moran, P. A. P. (1953). The statistical analysis of the Canadian lynx cycle. Aust. J. Zool. 1, 291–298.
Ott, E. and J. C. Sommerer (1994). Blowout bifurcations: the occurrence of riddled basins and on-off intermittency. Phys. Lett. A 188, 39–47.
Pecora, L. M. (1998). Synchronization conditions and desynchronizing patterns in coupled limit-cycle and chaotic systems. Phys. Rev. E 58, 347–360.
Pecora, L. M. and T. L. Carroll (1990). Synchronization in chaotic systems. Phys. Rev. Lett. 64, 821–825.
Pecora, L. M., T. L. Carroll and J. F. Heagy (1995). Statistics for mathematical properties of maps between time series embeddings. Phys. Rev. E 52, 3420–3439.
Pikovsky, A. S. (1984). On the interaction of strange attractors. Z. Phys. B 55, 149–154.
Pikovsky, A. S., M. G. Rosenblum, J. V. Osipov and J. Kurths (1997). Phase synchronization of chaotic oscillators by external driving. Physica D 104, 219–238.
Rössler, O. E. (1976). An equation for continuous chaos. Phys. Lett. A 57, 397–398.
Steele, J. H. and E. W. Henderson (1981). A simple plankton model. Am. Naturalist 14, 157–183.
Sughihara, G. and R. M. May (1990). Non-linear forecasting as a way of distinguishing chaos from measurement error. Nature 344, 734–741.
Wiggins, S. (1994). Normally Hyperbolic Invariant Manifolds in Dynamical Systems, Springer: New York.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hillary, R.M., Bees, M.A. Synchrony & chaos in patchy ecosystems. Bull. Math. Biol. 66, 1909–1931 (2004). https://doi.org/10.1016/j.bulm.2004.05.006
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1016/j.bulm.2004.05.006