Abstract
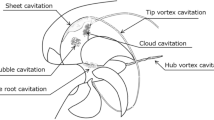
To clarify the influences of the tip clearance flows on the unsteady cavitating flow, the three-dimensional unsteady cavitating flows through both the two-dimensional cascades and the three-dimensional inducer with and without tip clearance are performed numerically. The governing equations for the compressible fluid flow with the DES turbulence model are employed with the assumption of the isentropic process of liquid phase. The evolution of cavities is represented as the source/sink of vapor phase. The basic equations in the curve linear coordinate are solved by the finite difference method. As the results of the three-dimensional cavitating flows through the two-dimensional cascades, the tip clearance flows from the pressure side to the suction side of the blade produces the tip vortex cavitation, which affects the sheet cavitation on the leading edge of the next blade and enhances the blockage effect near the casing than the flows without tip clearance. On the other hand, in the case of the three-dimensional inducer, the large backflow cavitation is observed around the inlet of the inducer, where the cavities are developed on the casing by the tip clearance flows. The large pressure gradient between the non-cavitating pressure side and the cavitating suction side enhances the tip clearance flows. The calculation considering the tip clearance reproduces the developed cavitation region similar to that of experimental visualizations. Additionally, the backflow cavitation rotates with the speed slower than the rotation speed of the inducer. Then, the rotation of backflow cavitation causes the periodic fluctuation of the outlet pressure greater than that of the inlet pressure.
Similar content being viewed by others
Abbreviations
- C:
-
Cord length, constant of cavitation model
- d:
-
Distance function
- d̃:
-
Length scale
- fL:
-
Volume fraction of liquid
- F:
-
External force
- g:
-
Metric tensor gmn = β m j β n j
- J:
-
Jacobian (J=|∂x i /∂ξj])
- k:
-
Turbulence kinematic energy
- M:
-
Mach number
- p:
-
Pressure
- Re:
-
Reynolds number
- S:
-
Magnitude of vorticity
- S̃:
-
Production
- u:
-
Velocity component on Cartesian coordinate
- U:
-
Contravariant velocity component on curvilinear coordinate
- t:
-
Time
- x:
-
Cartesian coordinate
- β:
-
Metric (β i j=∂ξj/∂x i )
- δ:
-
Dirac delta
- Δ:
-
Grid scale
- μ:
-
Viscosity
- ν:
-
Kinematic viscosity
- ρ:
-
Density
- σ:
-
Cavitation number
- τ:
-
Stress
- ω:
-
Vorticity
- Ω:
-
Cangular velocity
- ξ:
-
Curvilinear coordinate
References
KAMIJO K., YOSHIDA M. and TSUJIMOTO Y. Hydraulic and mechanical performance of LE-7 Lox pump inducer[J]. AIAA Journal of Propulsion and Power, 1993, 9(6): 819–826.
KUBOTA A. et al. A new modeling of cavitating flows: A numerical study of unsteady cavitation on a hydrofoil section[J]. J. Fluid Mech., 1992, 240: 59–96.
SCHNERR G. H. et al. Physical and numerical modeling of unsteady cavitation dynamics[C]. ICMF-2001. New Orleans, USA, 2001.
TAMURA Y. et al. Physical modeling and solution algorithm for cavitating flow simulations[C]. 15th Aiaa Cfd Conference. Anaheim, CA, USA, 2001, A01–31116.
REBOUD J. L., DELANNOY Y. Two-phase flow modeling of unsteady cavitation[C]. Proc. 2nd Int. Symp. on Cavitation. Tokyo, Japan, 1994, 39–44.
SHIN B. R., IKOHAGI T. Numerical analysis of unsteady cavity flows around a hydrofoil[C]. Proc. 3rd Int. Symp. on Cavitation. Grenoble, 1998, 301–306.
QIN J. R. et al. Numerical simulation of transient external and internal cavitating flows using the space-time conservation element and solution element method[C]. Proc. Asme FEDSM’01. New Orleans, LA, USA, 2001, FEDSM 2001–18011.
CHEN Y., HEISTER S. D. Two-phase modeling of cavitated flows[J]. Computers and Fluids, 1995, 24(7): 799–809.
SINGHAL A. K. et al. Mathematical basis and validation of the full cavitation model[C]. Asme Fluids Engineering Conference. Vancouver, Canada, 1997.
KUNZ R. F. et al. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J]. Computers and Fluids, 2000, 29(8): 849–857.
OKITA K. et al. Numerical analysis for cavitating flow in an axial pump[C]. 12th Symposium on Cavitation. Fukuoka, 2004, 13–16.
UGAJIN H. et al. Numerical analysis of the unsteady cavitating flow in a 2D-cascade and a 3D-inducer[C]. 43rd AIAA/ASME/SAE/Asee Joint Propulsion Conference and Exhibit. Cincinnati, 2007, Aiaa 2007–5535.
OKITA K., KAJISHIMA T. Numerical investigation of unsteady cavitating flow around a rectangular prism[C]. Proceedings of the 4th JSME-Ksme Thermal Engineering Conference. Kobe, Japan, 2000, 2: 571–576.
SPALART P. R. et al. Comments on the feasibility of Les for wings and on the hybrid RANS/Les approach[C]. Proceedings of the First Afosr International Conference on DNS/LES. Ruston, 1997.
SPALART P. R., ALLMARAS S. R. A one-equation turbulence model for aerodynamic flows[R]. Aiaa paper 92–0439, 1992.
OKITA K., KAJISHIMA T. Numerical simulation of unsteady cavitating flows around a hydrofoil[J]. Transaction of Jsme Series B, 2002, 68(667): 637–644.
Author information
Authors and Affiliations
Corresponding author
Additional information
Biography: OKITA K. (1974-), Male, Ph. D., Senior Scientist
Rights and permissions
About this article
Cite this article
Okita, K., Ugajin, H. & Matsumoto, Y. Numerical Analysis of the Influence of the Tip Clearance Flows on the Unsteady Cavitating Flows in a Three-Dimensional Inducer. J Hydrodyn 21, 34–40 (2009). https://doi.org/10.1016/S1001-6058(08)60116-X
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1016/S1001-6058(08)60116-X