Skip to main content
SpringerLink
Log in

Stochastic Analysis of Groundwater Flow Subject to Random Boundary Conditions

  • Published:
Journal of Hydrodynamics Aims and scope Submit manuscript

Abstract

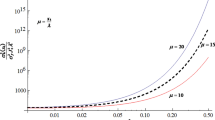
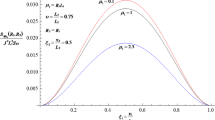
A stochastic model was developed to simulate the flow in heterogeneous media subject to random boundary conditions. Approximate partial differential equations were derived based on the Karhunen-Loeve (KL) expansion and perturbation expansion. The effect of random boundary conditions on the two-dimensional flow was examined. It is shown that the proposed stochastic model is efficient to include the random boundary conditions. The random boundaries lead to the increase of head variance and velocity variance. The influence of the random boundary conditions on head uncertainty is exerted over the whole simulated region, while the randomness of the boundary conditions leads to the increase of the velocity variance in the vicinity of boundaries.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. LIAO Hua-sheng, LI Shu-guang. Theoretically and numerically assessing the validity of Eulerian truncation in stochastic groundwater modeling [J]. Journal of Hydrodynamics, Ser. B, 2002, 14(3): 13–20.

    Google Scholar 

  2. YANG Jin-zhong, ZHANG Ren-duo and YE Zi-tong. Stochastic analyses of adsorbing solute transport in heterogeneous unsaturated soil [J]. Journal of Hydrodynamics, Ser. B, 1996, 8(3): 31–43.

    MATH  Google Scholar 

  3. YEH Tc. Jim. Stochastic modeling of groundwater flow and solute transport in aquifes [J]. Hydrological Processes, 2006, 6(4): 369–395.

    Google Scholar 

  4. YANG Jin-zhong, ZHANG Ren-duo and CAI Shu-ying et al. A conservation equation of concentration variance for solute transport in heterogeneous formations [J]. Journal of Hydrodynamics, Ser. B, 1998, 10(4): 16–30.

    MATH  Google Scholar 

  5. ZHANG D. X. Stochastic methods for flow in porous media: copying with uncertainties[M]. San Diego, CA: Academic Press, 2002.

    Google Scholar 

  6. BONILLA F. A., CUSHMAN J. H. Role of boundary conditions in convergence and nonlocality of solutions to stochastic flow problems in bounded domains [J]. Water Resour. Res., 2000, 36(4): 981–997.

    Article  Google Scholar 

  7. GUTJAHR A. L., GELHAR L. W. Stochastic models of subsurface flow: Infinite vs finite domains and stationarity [J]. Water Resour. Res., 1981, 17(2): 337–350.

    Article  Google Scholar 

  8. CHENG A. H., LAFE O. E. Boundary element solution for stochastic groundwater flow. Random boundary condition and recharge [J]. Water Resour. Res., 1991, 27(2): 231–242.

    Article  Google Scholar 

  9. ZHANG Dong-xiao, LU Zhi-ming. An efficient, high-order perturbation approach for flow in random porous media via Karhunen-Loeve and polynomial expansion [J]. J. Comput. Phys., 2004, 194: 773–794.

    Article  Google Scholar 

  10. YANG Jin-zhong, ZHANG Dong-xiao and LU Zhi-ming. Stochastic analysis of saturated-unsaturated flow in heterogeneous media by combining Karhunen-Loeve expansion and perturbation method [J]. J. Hydrol., 2003, 294(1-3): 18–38.

    Article  Google Scholar 

  11. YANG Jin-zhong, WANG Wei-ping and CAI Shu-ying et al. Stochastic analysis of water flow in heterogeneous media[J]. Journal of Hydrodynamics, Ser. B, 2005, 17(3): 313–322.

    MATH  Google Scholar 

  12. LIU Gai-sheng, ZHANG Dong-xiao and LU Zhi-ming. Stochastic uncertainty analysis for unconfined flow systems [J]. Water Resour. Res., 42 (9): W09412.1-W09412.18.

  13. BEAR J. Dynamics of fluids in porous media[M]. Mineola N Y: Dover, 1972.

    MATH  Google Scholar 

  14. GHANEM R. G., SPANOS P. D. Stochastic finite elements: A spectral approach [M]. New York: Springer Verlag, 1991.

    Book  Google Scholar 

  15. SIMUNEK J., VOGEL T. and Van GENUCHTEN M. The SWM_2D code for simulating water flow and solute transport in two-dimensional variably saturated media[R]. Version 1.1, Research Report No.126, US Salinity Lab, 1992.

    Google Scholar 

  16. LI Yong, WANG Chao. Theoretical estimation of groundwater discharge and associated nutrient loading to a lake with gentle slope bottom [J]. Journal of Hydrodynamics, Ser. B, 2007, 19(1): 30–35.

    Article  Google Scholar 

  17. ZHANG Xiang-wei, TAKEUCHI Kuniyoshi and CHEN Jing. Temporal and spatial discretization on quasi-3-D groundwater finite element modelling to avoid spurious oscillation [J]. Journal of Hydrodynamics, Ser. B, 2007, 19(1): 68–77.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan, 430072, China

    Liang-sheng Shi, Jin-zhong Yang, Shu-ying Cai & Lin Lin

Authors
  1. Liang-sheng Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jin-zhong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shu-ying Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lin Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liang-sheng Shi.

Additional information

Project supported by the National Natural Science Foundation of China ( Grant Nos. 40672164, 50379039).

Biography: SHI Liang-sheng (1982- ), Male, Ph. D.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shi, Ls., Yang, Jz., Cai, Sy. et al. Stochastic Analysis of Groundwater Flow Subject to Random Boundary Conditions. J Hydrodyn 20, 553–560 (2008). https://doi.org/10.1016/S1001-6058(08)60094-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S1001-6058(08)60094-3

Key words

Search

Navigation