Skip to main content
SpringerLink
Log in

The Flow Analysis of Fiuids in Fractal Reservoir with the Fractional Derivative

  • Published:
Journal of Hydrodynamics Aims and scope Submit manuscript

Abstract

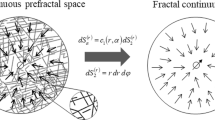
In this paper, fractional order derivative, fractal dimension and spectral dimension are introduced into the seepage flow mechanics to establish the flow models of fluids in fractal reservoirs with the fractional derivative. The flow characteristics of fluids through a fractal reservoir with the fractional order derivative are studied by using the finite integral transform, the discrete Laplace transform of sequential fractional derivatives and the generalized Mittag-Leffler function. Exact solutions are obtained for arbitrary fractional order derivative. The long-time and short-time asymptotic solutions for an infinite formation are also obtained. The pressure transient behavior of fluids flow through an infinite fractal reservoir is studied by using the Stehfest’ s inversion method of the numerical Laplace transform. It shows that the order of the fractional derivative affect the whole pressure behavior, particularly, the effect of pressure behavior of the early-time stage is larger The new type flow model of fluid in fractal reservoir with fractional derivative is provided a new mathematical model for studying the seepage mechanics of fluid in fractal porous media.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. CHANG J., YORTSOS Y. C. Pressure transient analysis of fractal reservoir[J]. Spe Formation Evaluation,1990, 5(1): 31–38.

    Article  Google Scholar 

  2. ACHNA J. A., ERSHAGH I., YORTSOS Y. C. Fractal analysis of pressure transient in the Geysers geothermal field[A]. 17th Annual Workshop Geothermal Reservoir Engineering[C]. Stanford, CA,1992.

    Google Scholar 

  3. ACUNA J. A., ERSHAGH I., YORTSOS Y. C. Practical application of fractal pressure transient analysis in naturally fractured reservoirs[J]. Spe Formation Evaluation, 1995 10(3): 173–179.

    Article  Google Scholar 

  4. TONG Deng-ke, GE Jia-li. An exact solution for unsteady seepage flow through fractal reservoir[J]. Acta Mechanica Sinica,1998,30(5): 621–627.(in Chinese)

    Google Scholar 

  5. TONG Deng-ke, CHEN Qin-lei. An exact solution and pressure characteristics of the flow of fluid through fractal reservoir[J]. Journal of Hydrodynamics, Ser.A, 1999,14(2): 201–209. (in Chinese)

    MathSciNet  Google Scholar 

  6. TONG Deng-ke, WANG Rui-he. Exact solution and dynamical characteristics of non-Newtonian power-law fluid flow in fractal reservoir.[J]. Journal of Hydrodynamics, Ser.A, 2000,15(3):342–350. (in Chinese)

    Google Scholar 

  7. TONG Deng-ke, WANG Rui-he. The line-source solution and flow analysis of fluid in fractal reservoir[J]. Journal of Hydrodynamics,Ser.B, 2002,14(4):59–65.

    Google Scholar 

  8. FRIEDRICH C. H. R. Relaxation and retardation functions of the Maxwell model with fractional derivatives[J]. Rheol. Acta, 1991,30(2):151–158.

    Article  Google Scholar 

  9. HUANG Jun-qi, LIU Ci-qun. Analysis of general second-order fluid flow in double cylinder rheometer[J]. Science in China, Ser. A,1996,26(10):912–920. (in Chinese)

    Google Scholar 

  10. TAN Wen-chang, XIAN feng, WEI Lan. The exact solution for unsteady Couette flow of generalized second order fluid[J]. Chinese Science Bulletin, 2002,47(16): 1226–1228. (in Chinese)

    MathSciNet  Google Scholar 

  11. XU Ming-yu, TAN Wen-chang. Theoretical analysis of the velocity field stress field and vortex sheet of generalized second order fluid with fractional anomalous diffusion[J]. Science in China, Ser. A, 2001,31(7):626–638. (in Chinese)

    MATH  Google Scholar 

  12. XU Ming-yu, TAN Wen-chang. The expression of generalized fractional element networks and generalized solution for the constitutive equation of viscoelastic materials[J]. Science in China, Ser. A, 2002,32(8):673–681.(in Chinese)

    Google Scholar 

  13. TONG Deng-ke, SHI Lina. The generalized flow analysis of non-Newtonian visco-elastic fluid flows in porous media[J].Journal of Hydrodynamics,Ser. A, 2005,19(6):695–701. (in Chinese)

    Google Scholar 

  14. PARK H. W., CHOE J., KANG J. M. Pressure behavior of transport in fractal porous media using a fractional calculus approach[J]. Energy Sources,2000, 22(10):881–890.

    Article  Google Scholar 

  15. SONG D. Y., JIANG T. Q. Study on the constitutive equation with fractional derivative for the vicoelastic fluids-Modified Jeffreys model and its application[J]. Rheologica Acta, 1998, 27:512–517.

    Article  Google Scholar 

  16. GE Jia-li, TONG deng-ke. The mechanics of nonlinear fluid for complex seepage system[M]. Dongying: Petroleum University Press, 1998. (in Chinese)

    Google Scholar 

  17. PODLUBNY I. Fractional differential equations[M]. San Diego: Academic Press, 1999.

    MATH  Google Scholar 

  18. TONG Deng-ke, CHEN Qin-lei. Generalized flow analysis of non-Newtonian visco-elastic fluid flow through fractal reservoir[J]. Applied Mathematics and Mechanics (English Edition), 1999, 20(12):1267–1274.

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mechanics, Chinese Academy of Science, Beijing, 100080, China

    Ji Tian

  2. Gudong Petroleum Factory of Shengli Petroleum Administration, Dongying, 256504, China

    Ji Tian

  3. Department of Applied Mathematics, China University of Petroleum, Dongying, 257061, China

    Deng-ke Tong

Authors
  1. Ji Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Deng-ke Tong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Deng-ke Tong.

Additional information

Project supported by the China National 973 Program (Grant No: 2002CB211708) and the Natural Science Foundation of Shandong Province (Grant No: Y2003F01).

Boigraphy: TIAN Ji (1964-), Male, Senior Engineering

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tian, J., Tong, Dk. The Flow Analysis of Fiuids in Fractal Reservoir with the Fractional Derivative. J Hydrodyn 18, 287–293 (2006). https://doi.org/10.1016/S1001-6058(06)60005-X

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S1001-6058(06)60005-X

Keywords

Search

Navigation