Skip to main content
SpringerLink
Log in

Two Kinds of Contact Problems in Dodecagonal Quasicrystals of Point Group 12 mm

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

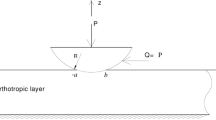
In this paper, two kinds of contact problems in 2-D dodecagonal quasicrystals were discussed using the complex variable function method: one is the finite frictional contact problem, the other is the adhesive contact problem. The analytic expressions of contact stresses in the phonon and phason fields were obtained for a flat rigid punch, which showed that: (1) for the finite frictional contact problem, the contact stress exhibited power-type singularities at the edge of the contact zone; (2) for the adhesive contact problem, the contact stress exhibited oscillatory singularities at the edge of the contact zone. The distribution regulation of contact stress under punch was illustrated; and the low friction property of quasicrystals was verified graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Shechtman, D., Blech, I., Gratias, D. and Cahn, J.W., Metallic phase with long-range orientational order and no translational symmetry. Physical Reviewer Letters, 1984, 53(20–22): 1951–1953.

    Article  Google Scholar 

  2. Fan, T.Y., and Mai, Y.W., Elasticity theory, fracture mechanics, and some relevant thermal properties of quasi-crystalline materials. Applied Mechanics Reviews, 2004, 57(5): 185–194.

    Article  Google Scholar 

  3. Ulrich, K., Franz, G. and Johannes, R. et al., Phason elastic constants of a binary tiling quasicrystal. Journal of Alloys and Compounds, 2002, 324 (1–2): 287–290.

    Google Scholar 

  4. Park, J.Y., Ogletree, D.F. and Salmeron, M. et al., Elastic and inelastic deformations of ethylene-passivated tenfold decagonal Al-Ni-Co quasicrystal surfaces. Physical Review B, 2005, 71(14): 144203.

    Google Scholar 

  5. Fan, T.Y., Mathematical Theory of Elasticity of Quasicrystals and Its Applications. Beijing: Science Press, 2010.

    MATH  Google Scholar 

  6. Guo, J.H., Jing, Y. and Riguleng, S., A semi-inverse method of a Griffith crack in one-dimensional hexagonal quasicrystals. Applied Mathematics and Computation, 2013, 219: 7445–7449

    Article  MathSciNet  Google Scholar 

  7. Li, X.Y., Elastic field in an infinite medium of one-dimensional hexagonal quasicrystal with a planar crack. International Journal of Solids and Structures, 2014, 51(6): 1442–1455.

    Article  Google Scholar 

  8. Zhang, L.L., Zhang, Y.M. and Gao, Y., General solutions of plane elasticity of one-dimensional orthorhombic quasicrystals with piezoelectric effect. Physics Letters A, 2014, 378(37): 2768–2776.

    Article  MathSciNet  Google Scholar 

  9. Fan, T.Y. and Guo, Y.C., Mathematical methods for a class of mixed boundary-value problems of planar pentagonal quasicrystal and some solutions. Science in China Series A: Mathematics, 1997, 40(9): 990–1003.

    Article  MathSciNet  Google Scholar 

  10. Yang, G., Zhao, B.S., Xu, S.P., A theory of general solutions of plane problems in two-dimensional octagonal quasicrystals. Journal of Elasticity, 2008, 93(3): 263–277.

    Article  MathSciNet  Google Scholar 

  11. Yang, L.Z., Gao, Y., Ernian, P. and Natalie, W., An exact solution for a multilayered two-dimensional decagonal quasicrystal plate. International Journal of Solids and Structures, 2014, 51(9): 1737–1749.

    Article  Google Scholar 

  12. Gao, Y., Xu, S.P. and Zhao, B.S., Stress and mixed boundary conditions for two dimensional decagonal quasicrystal plates. Pramana-Journal of Physics, 2007, 68(5): 803–817.

    Article  Google Scholar 

  13. Li, L.H. and Fan, T.Y., Final governing equation of plane elasticity of icosahedral quasicrystals and general solution based on stress potential function. Chinese Physical Letter, 2006, 23(9): 2519–2521.

    Article  Google Scholar 

  14. Gladwell GML( Chinese translation by Fan, T.Y.)., Contact problems in the classical elasticity theory. Beijing: Beijing Institute of Technology press, 1991.

  15. Galin, L.A., Contact Problems in the Theory of Elasticity. Moscow-Leningrad: Gostekhizdat (English translation by H. Moss, edited by I. N), 1953.

    Google Scholar 

  16. Johnson, K.L., Kendall, K. and Roberts, A.D., Surface energy and the contact of elastic solids. Proceedings of the Royal Society, 1971, 324(1558): 301–313.

    Article  Google Scholar 

  17. Sackfield, A.D., Hills, A. and NowelL, D., Mechanics of Elastic Contacts. London: Butterworth-Heinemann, 1993.

    MATH  Google Scholar 

  18. Maugis, D., Contact, Adhesion and Rupture of Elastic Solids. Berlin: Springer-Verlag, 2000.

    Book  Google Scholar 

  19. Muskhelishvili, N.T., Singular Integral Equations. Groningen: Noordhoff, 1953.

    MATH  Google Scholar 

  20. Peng, Y.Z. and Fan, T.Y., Crack and indentation problems for one-dimensional hexagonal quasicrystals. The European Physical Journal(B), 2001, 21(1): 39–44.

    Article  Google Scholar 

  21. Gao, Y. and Ricoeur, A., Three-dimensional Greens function for two-dimensional quasi-crystal bimaterials. Proceedings of the Royal Society (A), 2011, 467(2133): 2622–2642.

    Article  MathSciNet  Google Scholar 

  22. Wu, Y.F., Chen, W.Q. and Li, X.Y., Indentation on one-dimensional hexagonal quasicrystal general theory and complete exact solutions. Philosophical Magazine, 2013, 93(8): 858–882.

    Article  Google Scholar 

  23. Li, X.Y., Wu, Y.F. and Chen, W.Q., Indentation on two-dimensional hexagonal quasicrystals. Mechanics of Materials, 2014, 76: 121–136.

    Article  Google Scholar 

  24. Zhou, W.M., Contact Problem in decagonal two-dimensional quasicrystal. Journal of Beijing Institute of Technology, 2001, 10(1): 51–55 (in Chinese).

    MathSciNet  Google Scholar 

  25. Yin, S.Y., Zhou, W.M. and Fan, T.Y., Contact problem in octagonal two-dimensional quasierystalline material. Journal of Beijing Institute of Technology, 2001, 10(1): 51–55 (in Chinese).

    Google Scholar 

  26. Wang, X., Zhang, J.Q. and Guo, X.M., Two kinds of contact problems in decagonal quasicrystalline materials of point group 10 mm. Acta Mechanica Sinica, 2005, 37(2): 169–174 (in Chinese).

    Google Scholar 

  27. Zhou, W.M., Fan, T.Y. and Yin, S.Y., Axisymmetric contact problem of cubic quasicrystalline materials. Acta Mechanica Solida Sinica, 2002, 15(1): 68–74.

    Google Scholar 

  28. Krumeich, F., Muller, E.M. and Wepf, R.A. et al., The structure of dodecagonal (Ta, V)1.6Te imaged by phase-contrast scanning transmission electron microscopy. Journal of Solid State Chemistry, 2012, 194: 106–112.

    Article  Google Scholar 

  29. Chen, J., Ni, J.J. and Jin, W.L., Column tests of dodecagonal section double skin concrete-filled steel tubes. Thin-Walled Structures, 2015, 88: 28–40.

    Article  Google Scholar 

  30. Liu, G.T., Guo, R.P. and Fan, T.Y., The partition function and state equation of the point group 12mm two-dimensional dodecagonal quasicrystal. Thin-Walled Structures, 2003, 31(1): 25–27.

    Google Scholar 

  31. Jaric, M.V. and Nelson, D.R., Diffuse scattering from quasicrystals. Physical Review (B), 1988, 37(9–15): 4458–4472.

    Article  Google Scholar 

  32. Coddens, G., Bellissent, R., Calvayrac, Y. and Ambroise, J.P., Evidence for phason hopping in icosahedral AlFeCu quasi-crystals. Europhysics Letters, 1991, 16(3): 271–276.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Computer Science, Ningxia University, 750021, Yin Chuan, China

    Xuefen Zhao, Xing Li & Shenghu Ding

  2. Xinhua College, Ningxia University, 750021, Yin Chuan, China

    Xuefen Zhao

Authors
  1. Xuefen Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shenghu Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xing Li.

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 11362018, 11261045 and 11261401), and the Specialized Research Fund for the Doctoral Program of Higher Education of China (No. 20116401110002).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, X., Li, X. & Ding, S. Two Kinds of Contact Problems in Dodecagonal Quasicrystals of Point Group 12 mm. Acta Mech. Solida Sin. 29, 167–177 (2016). https://doi.org/10.1016/S0894-9166(16)30105-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S0894-9166(16)30105-7

Key Words

Search

Navigation