Skip to main content
SpringerLink
Log in

Numerical Simulation of Deformation Behavior of 22MnB5 Boron Steel at Elevated Temperatures and Experimental Verification

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

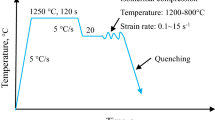
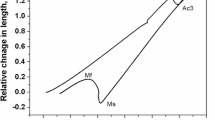
Abstract

The effects of strain, strain rate and temperature on the mechanical behavior of 22MnB5 boron steel deformed isothermally under uniaxial tension tests and the experimental characterization of 22MnB5 boron steel in the austenitic region have been investigated. Based on the crystal plasticity theory and thermal kinematics, an improved integration model is presented. In this model, the elastic deformation gradient is the integration variable of the governing equation, which contains not only the elastic deformation but also the thermal effects. In the coupled thermo-mechanical process, this model can reveal the evolution of microstructures such as the rotation of a single crystal and the slip systems in each of them. The plastic behavior of the boron steel can be well described by the presented model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Naderi, M., Durrenberger, L., Molinari, A. and Bleck, W., Constitutive relationships for 22MnB5 boron steel deformed isothermally at high temperatures. Materials Science and Engineering: A, 2008, 478(1–2): 130–139.

    Article  Google Scholar 

  2. Nikravesh, M., Naderi, M. and Akbari, G.H., Influence of hot plastic deformation and cooling rate on martensite and bainite start temperatures in 22MnB5 steel. Materials Science and Engineering: A, 2012, 540: 24–29.

    Article  Google Scholar 

  3. Abbasi, M., Saeed-Akbari, A. and Naderi, M., The effect of strain rate and deformation temperature on the characteristics of isothermally hot compressed boron-alloyed steel. Materials Science and Engineering: A, 2012, 538: 356–363.

    Article  Google Scholar 

  4. Johnson, G.R. and Cook, W.H., A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In: The 7th International Symposium on Ballistic. 1983: 541–547.

    Google Scholar 

  5. Khan, A.S. and Huang, S., Experimental and theoretical study of mechanical behavior of 1100 aluminum in the strain rate range 10−5–104 s−1. International Journal of Plasticity, 1992, 8(4): 397–424.

    Article  Google Scholar 

  6. Sung, J.H., Kim, J.H. and Wagoner, R.H., A plastic constitutive equation incorporating strain, strain-rate, and temperature. International Journal of Plasticity, 2010, 26(12): 1746–1771.

    Article  Google Scholar 

  7. Zerilli, F.J. and Armstrong, R.W., Dislocation-mechanics-based constitutive relations for material dynamics calculations. Journal of Applied Physics, 1987, 61(5): 1816–1825.

    Article  Google Scholar 

  8. Rusinek, A., Rodriguez-Martinez, J.A. and Arias, A., A thermo-viscoplastic constitutive model for FCC metals with application to OFHC copper. International Journal of Mechanical Sciences, 2010, 52(2): 120–135.

    Article  Google Scholar 

  9. Rodríguez-Martínez, J.A., Rodríguez-Millán, M., Rusinek, A. and Arias, A., A dislocation-based constitutive description for modeling the behaviour of FCC metals within wide ranges of strain rate and temperature. Mechanics of Materials, 2011, 43(12): 901–912.

    Article  Google Scholar 

  10. Anand, L., Constitutive equations for hot-working of metals. International Journal of Plasticity, 1985, 1(3): 213–231.

    Article  Google Scholar 

  11. Rashid, M.M. and Nemat-Nasser, S., A constitutive algorithm for rate-dependent crystal plasticity. Computer Methods in Applied Mechanics and Engineering, 1992, 94(2): 201–228.

    Article  Google Scholar 

  12. Ganapathysubramanian, S. and Zabaras, N., Modeling the thermoelastic-viscoplastic response of polycrystals using a continuum representation over the orientation space. International Journal of Plasticity, 2005, 21(1): 119–144.

    Article  Google Scholar 

  13. Roters, F., Eisenlohr, P., Hantcherli, L., Tjahjanto, D.D., Bieler, T.R. and Raabe, D., Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Materialia, 2010, 58(4): 1152–1211.

    Article  Google Scholar 

  14. Peirce, D., Shear band bifurcations in ductile single crystals. Journal of the Mechanics and Physics of Solids, 1983, 31(2): 133–153.

    Article  Google Scholar 

  15. Kalidindi, S.R., Bronkhorst, C.A. and Anand, L., Crystallographic texture evolution in bulk deformation processing of FCC metals. Journal of the Mechanics and Physics of Solids, 1992, 40(3): 537–569.

    Article  Google Scholar 

  16. Sarma, G. and Zacharia, T., Integration algorithm for modeling the elasto-viscoplastic response of polycrystalline materials. Journal of the Mechanics and Physics of Solids, 1999, 47(6): 1219–1238.

    Article  Google Scholar 

  17. Maniatty, A.M., Dawson, P.R. and Lee, Y.S., A time integration algorithm for elasto-viscoplastic cubic crystals applied to modelling polycrystalline deformation. International Journal for Numerical Methods in Engineering, 1992, 35(8): 1565–1588.

    Article  Google Scholar 

  18. Ganapathysubramanian, S. and Zabaras, N., A continuum sensitivity method for finite thermo-inelastic deformations with applications to the design of hot forming processes. International Journal for Numerical Methods in Engineering, 2002, 55(12): 1391–1437.

    Article  Google Scholar 

  19. Meissonnier, F.T., Busso, E.P. and O’Dowd, N.P., Finite element implementation of a generalised non-local rate-dependent crystallographic formulation for finite strains. International Journal of Plasticity, 2001, 17(4): 601–640.

    Article  Google Scholar 

  20. Hutchinson, J.W., Bounds and self-consistent estimates for creep of polycrystalline materials. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 1976, 348(1652): 101–127.

    Article  Google Scholar 

  21. Pan, J. and Rice, J.R., Rate sensitivity of plastic flow and implications for yield-surface vertices. International Journal of Solids and Structures, 1983, 19(11): 973–987.

    Article  Google Scholar 

  22. Mathur, K.K. and Dawson, P.R., On modeling the development of crystallographic texture in bulk forming processes. International Journal of Plasticity, 1989, 5(1): 67–94.

    Article  Google Scholar 

  23. Hu, P., Ma, N., Liu, L. and Zhu, Y., Theories, Methods and Numerical Technology of Sheet Metal Cold and Hot Forming: Analysis, Simulation and Engineering Applications. Springer Press, 2012: 101–103.

  24. Zhao, D., Zhu, Y.G., Hu, P. and Zhang, W.X., Constitutive model of single crystal thermal finite deformation. Acta Mechanica Solida Sinica, 2013, 3: 266–271 (in Chinese).

    Article  Google Scholar 

  25. Taylor, G.I., Plasticity strain in metals. Journal of Institute of Metals, 1938, 62: 307–324.

    Google Scholar 

  26. Sachs, G., Zur ableitung einer fliessbedingung. Zeitschrift Vereines Deutscher Ingenieure, 1928, 72(103): 734–736.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Structural Analysis for Industrial Equipment, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, 2 Linggong Road, Dalian, 116023, China

    Dan Zhao, Yiguo Zhu, Liang Ying, Ping Hu, Ying Chang & Wanxi Zhang

Authors
  1. Dan Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yiguo Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liang Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ping Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ying Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Wanxi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yiguo Zhu.

Additional information

This work is funded by the Key Project of the National Natural Science Foundation of China (Nos. 10932003 and 11272075), Project of Chinese National Programs for Fundamental Research and Development (Nos. 2012CB619603 and 2010CB832700) and ‘04’ Great Project of Ministry of Industrialization and Information of China (No. 2011ZX04001-21).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, D., Zhu, Y., Ying, L. et al. Numerical Simulation of Deformation Behavior of 22MnB5 Boron Steel at Elevated Temperatures and Experimental Verification. Acta Mech. Solida Sin. 27, 579–587 (2014). https://doi.org/10.1016/S0894-9166(15)60003-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S0894-9166(15)60003-9

Key Words

Search

Navigation