Abstract
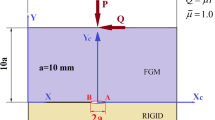
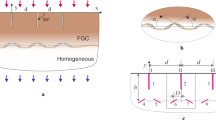
In this paper, a finite crack with constant length (Yoffe type crack) propagating in a functionally graded coating with spatially varying elastic properties bonded to a homogeneous substrate of finite thickness under anti-plane loading was studied. A multi-layered model is employed to model arbitrary variations of material properties based on two linearly-distributed material compliance parameters. The mixed boundary problem is reduced to a system of singular integral equations that are solved numerically. Some numerical examples are given to demonstrate the accuracy, efficiency and versatility of the model. The numerical results show that the graded parameters, the thicknesses of the interfacial layer and the two homogeneous layers, the crack size and speed have significant effects on the dynamic fracture behavior.
Article PDF
Similar content being viewed by others
References
Sih, G.C. and Chen, E.P., Moving cracks in layered composites. International Journal of Engineering Sciences, 1982, 20(12): 1181–1192.
Meguid, S.A., Wang, X.D. and Jiang, L.Y., On the dynamic propagation of a finite crack in functionally graded materials. Engineering Fracture Mechanics, 2002, 69: 1753–1768.
Jiang, L.Y. and Wang, X.D., On the dynamic crack propagation in an interphase with spatially varying elastic properties under inplane loading. International Journal Fracture, 2002, 114(3): 225–244.
Bi, X.S., Cheng, J. and Chen, X.L., Moving crack for functionally graded material in an infinite length strip under anti-plane shear. Theoretical and Applied Fracture Mechanics, 2003, 39(1): 89–97.
Guo, L.C., Wu, L.Z., Sun, Y.G. and Ma, L., The transient fracture behavior for a functionally graded layered structures subjected to an in-plane impact load. Acta Mechanica Sinica, 2005, 21(3): 257–266.
Singh, B.M., Rokne, J., Vrbik, J. and Dhaliwal, R.S., Finite Griffith crack propagating in a non-homogeneous medium. European Journal of Mechanics A/Solids, 2006, 25(5): 867–875.
Cheng, Z.Q. and Zhong, Z., Analysis of a moving crack in a functionally graded strip between two homogeneous layers. International Journal of Mechanical Sciences, 2007, 49(9): 1038–1046.
Lee, K.H., Lee, Y.J. and Cho, B.S., Characteristic of a transiently propagating crack in functionally graded materials. Journal of Mechanical Science and Technology, 2009, 23(5): 1306–1322.
Lee, K.H., Analysis of transiently propagating crack in functionally graded materials under mode I and II. International Journal of Engineering Sciences, 2009, 47(9): 852–865.
Parameswaran, V. and Shukla, A., Dynamic fracture of a functionally gradient material having discrete property variation. Journal of Material Science, 1998, 33(13): 3303–3311.
Jain, N. and Shukla, A., Mixed mode dynamic fracture in particulate reinforced functionally graded materials. Experimental Mechanics, 2006, 46(2): 137–154.
Shukla, A. and Jain, N., Dynamic damage growth in particle reinforced graded materials. International Journal of impact engineering, 2004, 30(7): 777–803.
Itou, S., Stress intensity factors around a crack in a nonhomogeneous interfacial layers between two dissimilar elastic half-plane. International Journal Fracture, 2001, 110(2): 123–135.
Wang, B.L., Mai, Y.W. and Noda, N., Fracture mechanics analysis model for FGM with arbitrary distributed properties. International Journal Fracture, 2002, 116(2): 161–177.
Wang, Y.S. and Gross, D., On the mechanical modeling of functionally graded interfacial zone with a Griffith crack: plane deformation. International Journal Fracture, 2004, 125(1–2): 189–205.
Huang, G.Y., Wang, Y.S. and Yu, S.W., A new model for fracture analysis of functionally graded coatings under plane deformation. Mechanics of Material, 2005, 37(4): 507–516.
Cheng, Z.Q. and Zhong, Z., Fracture analysis of a functionally graded strip under plane deformation. Acta Mechanica Solida Sinica, 2006, 19(2): 114–121.
Zhong, Z. and Cheng, Z.Q., Fracture analysis of a functionally graded strip with arbitrary distributed material properties. International Journal of Solids and Structure, 2008, 45(13): 3711–3725.
Erdogan, F. and Gupta, G.D., On the numerical solution of singular integral equations. Quarterly Journal of Applied Mathematics, 1972, 29(1): 525–534.
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Nos. 10802078 and 10872150) and China Postdoctoral Science Foundation (No. 20100471006).
Rights and permissions
About this article
Cite this article
Cheng, Z., Gao, D. & Zhong, Z. Crack Propagating in Functionally Graded Coating with Arbitrarily Distributed Material Properties Bonded to Homogeneous Substrate. Acta Mech. Solida Sin. 23, 437–446 (2010). https://doi.org/10.1016/S0894-9166(10)60046-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1016/S0894-9166(10)60046-8