${\mathcal {C}}_1$-diagrams of slim rectangular semimodular lattices permit quotient diagrams

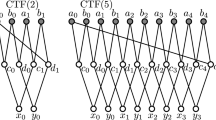
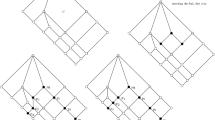
Abstract

Slim semimodular lattices (for short, SPS lattices) and slim rectangular lattices (for short, SR lattices) were introduced by Grätzer and Knapp (Acta Sci Math (Szeged) 73:445–462, 2007; 75:29–48, 2009). These lattices are necessarily finite and planar, and they have been studied in more then four dozen papers since 2007. They are best understood with the help of their ${\mathcal {C}}_1$-diagrams, introduced by the author in 2017. For a diagram F of a finite lattice L and a congruence $\alpha$ of L, we define the “quotient diagram” $F/\alpha$ by taking the maximal elements of the $\alpha$-blocks and preserving their geometric positions. While $F/\alpha$ is not even a Hasse diagram in general, we prove that whenever L is an SR lattice and F is a ${\mathcal {C}}_1$-diagram of L, then $F/\alpha$ is a ${\mathcal {C}}_1$-diagram of $L/\alpha$, which is an SR lattice or a chain. The class of lattices isomorphic to the congruence lattices of SPS lattices is closed under taking filters. We prove that this class is closed under two more constructions, which are inverses of taking filters in some sense; one of the two respective proofs relies on an inverse of the quotient diagram construction.