Abstract
In this paper, we derive a new reconstruction method for real non-harmonic Fourier sums, i.e., real signals which can be represented as sparse exponential sums of the form \(f(t) = \sum _{j=1}^{K} \gamma _{j} \, \cos (2\pi a_{j} t + b_{j})\), where the frequency parameters \(a_{j} \in {\mathbb {R}}\) (or \(a_{j} \in {\mathrm i} {\mathbb {R}}\)) are pairwise different. Our method is based on the recently proposed numerically stable iterative rational approximation algorithm in Nakatsukasa et al. (SIAM J Sci Comput 40(3):A1494–A1522, 2018). For signal reconstruction we use a set of classical Fourier coefficients of f with regard to a fixed interval (0, P) with \(P>0\). Even though all terms of f may be non-P-periodic, our reconstruction method requires at most \(2K+2\) Fourier coefficients \(c_{n}(f)\) to recover all parameters of f. We show that in the case of exact data, the proposed iterative algorithm terminates after at most \(K+1\) steps. The algorithm can also detect the number K of terms of f, if K is a priori unknown and \(L \ge 2K+2\) Fourier coefficients are available. Therefore our method provides a new alternative to the known numerical approaches for the recovery of exponential sums that are based on Prony’s method.
Similar content being viewed by others
1 Introduction
Classical Fourier analysis methods provide for any real square integrable signal f(t) a Fourier series representation on a given interval (0, P), \(P>0\), of the form
with Fourier coefficients
and \(\alpha _{n}=2\, |c_{n}(f)|\), \(\beta _{n} = \mathop {\mathrm {atan2}}(\mathrm {Im} \, c_{n}(f), \mathrm {Re} \, c_{n}(f))\) for \(n \ge 0\), where \(\mathop {\mathrm {atan2}}\) denotes the modified inverse tangent, see e.g. [23, Chapter 1]. If f is P-periodic and differentiable, then its Fourier series (1.1) converges uniformly to f. However, if f is smooth but not P-periodic, then the P-periodization of f “forced” by the Fourier series representation in (1.1) usually leads to a discontinuity at the interval boundaries \(t=0\) and \(t=P\), respectively, and thus to a slow decay of the Fourier coefficients.
In applications, it frequently happens that a signal is only given on an interval of length P, where it appears to be non-periodic, even if f may be periodic with a certain period \(P_{1}\) which is not of the form P/n for some positive integer n. Considering for example the signal
which contains only two different frequency parameters, we observe that this signal is non-periodic with regard to any interval (0, P). For \(P=1\), the corresponding Fourier series is given by
Thus, the question occurs, how to reconstruct a non-harmonic Fourier sum, i.e., how to compute the much more informative representation (1.2) directly from suitable measurements of f.
Contents of this paper The goal of this paper is to reconstruct non-harmonic Fourier sums f of the form
from a finite number of its classical Fourier coefficients \(c_{n}(f)\) corresponding to a Fourier series of f on (0, P). Here, we assume that \(K \in {\mathbb {N}}\), \(\gamma _{j} \in (0, \infty )\), \((a_{j}, \, b_{j}) \in (0, \infty ) \times [0, \, 2\pi )\), and that the frequency parameters \(a_{j}\) are pairwise distinct. As we will show in the sequel, the restrictions made for \(K, \, \gamma _{j}, \, a_{j}\), and \(b_{j}\) will ensure uniqueness of the presentation (1.3). Note that f in (1.3) admits real (nonnegative) frequency parameters \(a_{j}\) and therefore essentially generalizes usual trigonometric polynomials. The example in (1.2) with frequencies \(\sqrt{2}\) and \(\sqrt{3}\) is covered by our model (1.3) taking \(K=2\), \(\gamma _{1}= \gamma _{2} = 1\), \(a_{1}= \sqrt{2}\), \(a_{2} =\sqrt{3}\), and \(b_{1}=b_{2}=0\). Observe that the function f in (1.3) is only P-periodic for some \(P >0\) if all parameters \(a_{j}\) can be written in the form \(a_{j} = c \, q_{j}\) with a positive constant \(c \in {\mathbb {R}}\) and rational numbers \(q_{j} \ge 0\), i.e., only in this case, there exists a real number \(P >0\) such that \(f(t+P) = f(t)\) for all \(t \in {\mathbb {R}}\).
In Sect. 2 we show that our model (1.3) is well-defined, i.e., that all parameters \(K, a_{j}, \, b_{j}, \gamma _{j}\), \(j=1,\ldots , K\), are (with the given restrictions) uniquely determined for a non-harmonic Fourier sum f. If all terms \(f_{j}\) of f are non-P-periodic, i.e., if all frequency parameters \(a_{j} > 0\) in (1.3) satisfy that \(a_{j} \not \in \frac{1}{P} {\mathbb {N}}\), then we can show that the modified Fourier coefficients \(\tilde{c}_{n}(f) := \text {Re}\, c_{n}(f) + \frac{\mathrm {i}}{n} \text {Im} \, c_{n}(f)\), \(n >0\), have a special structure of the form \(r(n^{2})\), where r(z) is a rational function of type \((K-1,K)\). Conversely, r(z) already provides all information to find the parameters determining f in (1.3).
Section 3 is devoted to the new reconstruction method. Using a modification of the recently proposed AAA algorithm for iterative rational approximation, see [20], we compute r(z) from a set of (at least) \(2K+1\) classical Fourier coefficients of f. Then a partial fraction decomposition together with a non-linear bijective transform provides the wanted parameters in (1.3). Numerical stability of the rational approximation algorithm is ensured using a barycentric representation of the numerator and the denominator polynomial of r(z). Compared to other rational interpolation algorithms, a further important advantage of the employed modified AAA algorithm is that we do not need a priori knowledge on the number K of terms in (1.3) but can determine K in the iteration process, supposed that \(L \ge 2K+1\) Fourier coefficients are available.
We show in Sect. 4, that a signal f with K non-P-periodic terms \(f_{j}\) as in (1.3) can theoretically be determined from 2K Fourier coefficients \(c_{n}(f)\) with \(n \in \Gamma \subset {\mathbb {N}}\) if K is known beforehand. If \(L \ge 2K+1\) Fourier coefficients are available, then our method based on the AAA algorithm always provides the wanted rational function r(z) after K iteration steps (and using \(2K+1\) modified Fourier coefficients). Thereby, also the number K of terms in (1.3) is determined.
In Sect. 5, our new reconstruction method is generalized to the case that f in (1.3) also contains P-periodic terms \(f_{j}\) with frequencies \(a_{j} \in \frac{1}{P} {\mathbb {N}}\). It turns out that there is no a priori information needed about possibly occurring P-periodic terms of f. In this case, we first compute the rational function r(z) that determines the non-P-periodic part of f, where we again employ the modified AAA algorithm from Sect. 3. Afterwards, the P-periodic terms of f can be found in a post-processing step, if all \(c_{n_{j}}(f)\) with \(n_{j} = Pa_{j}\) are contained in the given set of Fourier coefficients. In particular, we show that f can be always completely recovered from \(L \ge 2K+2\) Fourier coefficients, i.e., our method determines the number K of terms as well as all parameters \(\gamma _{j}\), \(a_{j}\) and \(b_{j}\), \(j=1, \ldots , K\), and automatically recognizes frequencies \(a_{j} \in \frac{1}{P}{\mathbb {N}}\) that correspond to P-periodic terms.
In Sect. 6, we generalize the model in (1.3). Beside supposing \((a_{j}, \, b_{j}) \in (0, \infty ) \times [0, 2\pi )\), we can also admit parameters \((a_{j}, \, b_{j}) \in {\mathrm i} (0, \infty ) \times {\mathrm i} {\mathbb {R}}\). By \(\cos ({\mathrm i}x) = \cosh (x)\), this leads to terms of the form \(\gamma _{j}\cosh ((-{\mathrm i})(2\pi a_{j} + b_{j})\) in (1.3). The considered generalization still admits the same rational structure of Fourier coefficients and can therefore be treated similarly as (1.3) with the proposed reconstruction method.
Finally we provide some numerical experiments. The Matlab implementation of our reconstruction algorithm is provided at the Software section of our homepagehttp://na.math.uni-goettingen.de.
Related literature Our model (1.3) can be viewed as a sparse expansion into exponentials with 2K terms via Euler’s identity, i.e.,
The problem of parameter identification of exponential sums from suitable input values appears in many applications as e.g. sparse array of arrival estimation [18], image super-resolution [32], nondestructive testing [5], system theory for parametrized model reduction [15], and phase retrieval [1]. Exponential sums have been extensively studied within the last years, based on Prony’s method and its relatives, see e.g. [2, 4, 7, 11, 21, 24,25,26,27, 29, 31, 34]. To reconstruct an exponential sum via Prony’s method, one usually employs equidistant function values \(f(t_{0} + h\ell )\), \(\ell = 0, \ldots , L\), and the number of given values should be at least 2M, where M is the number of terms in the exponential sum. In our case, the number of exponential terms is \(M=2K\), but the symmetry properties can be exploited such that the samples \(f(h\ell )\), \(\ell =0, \ldots , 2K-1\), are theoretically sufficient for the recovery of f in the noise-free case, see e.g. [24]. However, Prony’s method involves Hankel or Toeplitz matrices with possibly high condition numbers, and therefore requires a very careful numerical treatment. Our new method for reconstruction of signals of the form (1.3) in this paper is based on rational approximation and can be seen as a good alternative to the Prony reconstruction approach.
Another way to look at the model (1.3) is to view it as a special case of a signal decomposition into so-called intrinsic mode functions (IMFs) in adaptive data analysis, see [14]. Empirical mode decomposition (EMD) is based on a model that decomposes the signal f into K IMFs,
with nonnegative envelope functions \(\gamma _{j}(t)\) and so-called instantaneous phase functions \(\phi _{j}(t)\), see e.g. [14]. As already pointed out in [8], despite certain restrictions, as e.g. that \(\gamma _{j}(t)\) and \(\phi _{j}(t)\) are smooth with \(\gamma _{j}(t) \ge 0\) and \(\phi _{j}'(t) \ge 0\) for \(t \in {\mathbb {R}}\), a representation of the form (1.4) is far from being unique. For example, the function f(t) in (1.2) has the form (1.4) with \(K=2\), constant functions \(\gamma _{1}(t)\), \(\gamma _{2}(t)\), and with \(\phi _{1}(t)= 2\pi \, \sqrt{2}t\) and \(\phi _{2}(t)= 2\pi \, \sqrt{3}t\). However, f(t) in (1.2) can also be written as a single IMF in \(\Big [- \frac{\sqrt{3} + \sqrt{2}}{4}, \frac{\sqrt{3} + \sqrt{2}}{4}\Big ]\),
The non-uniqueness of the model (1.4) often prevents a simple interpretation of the obtained decomposition.
Compared to (1.4), the main advantages of the non-harmonic Fourier sum (1.3) are that the representation of f is unique, and, that the model (1.3) has a direct physical interpretation, similarly to classical Fourier sums.
There are also other approaches to represent signals by adaptive generalized Fourier sums using the so-called Takenaka–Malmquist basis, an adaptive orthonormal basis, see [22, 28]. While the greedy algorithm in [28] only slightly improves the signal approximation compared to classical Fourier sums, it has been shown in [22], that strong decays of adaptive Fourier expansions can be achieved, if the sequence of classical Fourier coefficients of a signal can be well approximated using a short exponential sum. Our approach in the current paper is somehow vice versa, the (modified) Fourier coefficients of f are represented by rational functions in order to reconstruct the special exponential sum f.
While we focus on signal reconstruction in the current paper, there remains the question of (almost) optimal signal approximation by non-harmonic Fourier sums, which we will study in the future. Obviously, each square integrable signal in (0, P) can be arbitrarily well approximated be a non-harmonic Fourier sum (1.3) for \(K \rightarrow \infty \), since it is a direct generalization of classical Fourier sums. However, approximation rates for signals in certain function classes are not completely known so far. Research on non-harmonic Fourier series particularly focussed on functional analytic questions, see e.g. [33]. In particular, it has been shown that \(\{{\mathrm e}^{2\pi {\mathrm i}a_{j} \cdot } \}_{j \in {\mathbb Z}}\) forms a Riesz basis in \(L^{2}([0,1])\) for a given increasing sequence \(\{ a_{j}\}_{j \in {\mathbb Z}}\) if and only if \(|a_{j} - j| < 1/4\) for \(j \in {\mathbb Z}\), see [16], while completeness of this function system is ensured for \(|a_{j}| \le |j| + 1/4\), where \(a_{j}\) can even be complex, see [19]. Note that for finite non-harmonic Fourier sums as in (1.3) we do not need any further assumption on the distribution of (pairwise distinct) frequencies to ensure the uniqueness of the presentation.
2 Non-harmonic signals
We consider signals f of the form (1.3) with \(K \in {\mathbb {N}}\), \(\gamma _{j} \in (0, \infty )\), and \((a_{j}, \, b_{j}) \in (0, \infty ) \times [0, \, 2\pi )\), and we assume that the parameters \(a_{j}\), \(j=1, \ldots , K\), are pairwise distinct.
2.1 Unique representation of non-harmonic signals
We will show that the model in (1.3) is well-defined, since all occurring parameters \(K, \, \gamma _{j}, \, a_{j}\) and \(b_{j}\), \(j=1, \ldots , K\), are uniquely determined for a function f given on an interval with positive length. More precisely, we can show the following:
Theorem 2.1
The representation of each function of the form (1.3) is unique. More exactly, for f as given in (1.3) the parameter \(K \in {\mathbb {N}}\), as well as the parameters \(\gamma _j \in (0, \infty )\), \(b_{j} \in [0, 2\pi )\), \(j=1, \ldots , K\), and \(0< a_{1}< a_{2}< \cdots< a_{K}< \infty \) are uniquely defined from the function values f(t) for \(t \in T\), where \(T \subset {\mathbb {R}}\) is an interval of positive length.
Proof
Consider f in (1.3) with parameters \(K \in {\mathbb {N}}\), \(\gamma _j \in (0, \infty )\), \(b_{j} \in [0, 2\pi )\), \(j=1, \ldots , K\), and \(0< a_{1}< a_{2}< \cdots< a_{K}< \infty \). Further, let
with \(M \in {\mathbb {N}}\), \(\delta _j \in (0, \infty )\), \(d_{j} \in [0, 2\pi )\), \(j=0, \ldots , M\), and \(0< c_{1 }< c_{2}< \cdots< c_{M} < \infty \). We will show: If \(f(t) = g(t)\) for all t on an interval \(T \subset {\mathbb {R}}\) of positive length, then we have \(K=M\) and \(\gamma _{j}=\delta _{j}\), \(a_{j}=c_{j}\), \(b_{j}= d_{j}\) for \(j=1, \ldots , K\).
1. We consider \(h(t) = f(t) - g(t)\). Then \(h(t) = 0\) for all \(t \in T\), and h(t) has the structure
with
By assumption, the number L of distinct frequency parameters \(x_{j}\) in the representation (2.1) of h satisfies \(L \ge \max \{K, \, M\}\), and we can rewrite h(t) in the form
where \(\tilde{x}_{\ell } \in \{ x_{j}: \, j=1, \ldots , K+M\}\) are now pairwise distinct. If \(\tilde{x}_{\ell }\) occurs only once in the set \(\{ x_{j}: \, j=1, \ldots , K+M \} \), say \(\tilde{x}_{\ell } = x_{j}\), then
If \(\tilde{x}_{\ell }\) occurs twice in the set \(\{ x_{j}: \, j=1, \ldots , K+M \} \), say \(\tilde{x}_{\ell }= x_{j_{1}}= x_{K+j_{2}}\), with \(j_{1} \in \{1, \ldots , K\}\) and \(j_{2} \in \{1, \ldots , M\}\), then
2. We show that the 2L functions \(\{ \cos (2\pi \tilde{x}_{\ell } t), \, \sin (2\pi \tilde{x}_{\ell }t): \, \ell =1, \ldots , L\}\) occurring in (2.2), are linearly independent on T. By Euler’s identity there is an invertible transform from this function set to \(\{ {\mathrm e}^{2\pi {\mathrm i} \tilde{x}_{\ell }t}, \, {\mathrm e}^{-2\pi {\mathrm i} \tilde{x}_{\ell }t}: \, \ell =1, \ldots , L\}\), i.e., h(t) in (2.2) can also be written as
with \(\tilde{x}_{L+\ell } :=-\tilde{x}_{\ell }\) and with \({\xi }_{\ell } = \alpha _{\ell } + {\mathrm i} \beta _{\ell }\) as well as \({\xi }_{L+\ell } = \alpha _{\ell } - {\mathrm i} \beta _{\ell }\), \(\ell =1, \ldots , L\). We obtain for the Wronskian of the function system \(\{ {\mathrm e}^{2\pi {\mathrm i} \tilde{x}_{\ell } t}: \, \ell =1, \ldots , 2L\}\) that
for all \(t \in T \subset {\mathbb {R}}\), since the Vandermonde matrix \(\left( \tilde{x}_{\ell }^{k} \right) _{k=0,\ell =1}^{2L-1,2L}\) is invertible for pairwise distinct \(\tilde{x}_{\ell }\), \(\ell =1, \ldots , 2L\), and we have \(\prod \nolimits _{\ell =1}^{2L} {\mathrm e}^{2\pi {\mathrm i} \tilde{x}_{\ell }t} = \prod \nolimits _{\ell =1}^{L} {\mathrm e}^{2\pi {\mathrm i} \tilde{x}_{\ell }t} {\mathrm e}^{-2\pi {\mathrm i} \tilde{x}_{\ell }t} = 1\). Thus, linear independence of \({\mathrm e}^{2\pi {\mathrm i} \tilde{x}_{\ell }t}\), \(\ell =1, \ldots , 2L\), and hence of \(\cos (2\pi \tilde{x}_{\ell } t), \, \sin (2\pi \tilde{x}_{\ell }t)\), \(\ell =1, \ldots , L\), follows. Therefore, \(h(t)=0\) on T directly implies that \(\alpha _{\ell } = \beta _{\ell }=0\) for \(\ell =1, \ldots , L\).
3. Now, if \(\tilde{x}_{\ell }\) would occur only once in the set \(\{ x_{j}: \, j=1, \dots , K+M\}\), say \(\tilde{x}_{\ell } = x_{j}\), then \(\alpha _{\ell } = \beta _{\ell } =0\) implies \(\mu _{j} \, \cos (y_{j})=0\) and \(\mu _{j} \, \sin (y_{j}) =0\), and thus \(\mu _{j}=0\) contradicting the assumption. Therefore, \(\tilde{x}_{\ell }\) always occurs twice, and it follows already that \(K=M=L\). Let \(\tilde{x}_{\ell }= x_{j_{1}}= x_{K+j_{2}}\), with \(j_{1}, \, j_{2} \in \{1, \ldots , K\}\). Thus we find \(a_{j_{1}} = c_{j_{2}}\). Further, \(\alpha _{\ell } = \beta _{\ell } =0\) implies by (2.3) that
We use the assumption \(y_{j_{1}}=b_{j_{1}} \in [0, 2\pi )\) and \(y_{K+j_{2}} = d_{j_{2}} \in [0, 2\pi )\), and conclude from \(y_{j_{1}}-y_{K+j_{2}} \in \{-\pi , \, 0,\, \pi \}\) that either \(b_{j_{1}} = d_{j_{2}}\) or \(b_{j_{1}} = d_{j_{2}} + \pi \, \mathrm {mod} \, 2\pi \). However, in the second case it would follow that \(\cos d_{j_{2}} = - \cos b_{j_{1}}\) and \(\sin d_{j_{2}} = - \sin b_{j_{2}}\), and thus by (2.3)
contradicting the assumption \(\mu _{j_{1}}=\gamma _{j_{1}} >0\) and \(\mu _{K+j_{2}} = -\delta _{j_{2}} <0\). Hence, \(b_{j_{1}} = d_{j_{2}}\) and \(\gamma _{j_{1}} = \delta _{j_{2}}\). Since these conclusions are valid for each \(\tilde{x}_{\ell }\), the assertion of the theorem follows.
Remark 2.2
1. Theorem 2.1 also shows that a function f of the form (1.3) with the given restrictions on the parameters \(\gamma _{j}, \, a_{j}, \, b_{j}\) cannot vanish on any interval \(T \subset {\mathbb {R}}\) with positive length.
2. Since \(\cos (2\pi a_{j}t)\) and thus also the functions f, g and h in the proof of Theorem 2.1 are analytic functions, the assumption \(h(t) = 0\) for \(t \in T\) already implies \(h(t)=0\) for \(t \in {\mathbb C}\).
3. The linear independence of the system \(\{ {\mathrm e}^{2\pi {\mathrm i} \tilde{x}_{\ell } t}, \, {\mathrm e}^{-2\pi {\mathrm i} \tilde{x}_{\ell } t}: \, \ell =1, \ldots , L\}\) in the proof of Theorem 2.1 also follows from the fact that an exponential sum of the form h(t) in (2.4) can appear as a general solution of a linear difference equation of order 2L with constant coefficients, see e.g. [3].
4. Observe that the function model can simply be extended by adding a constant component \(f_{0}(t) = \pm \gamma _{0} = \gamma _{0} \, \cos (2\pi a_{0} t + b_{0})\) with \(\gamma _{0} >0\), \(a_{0}=0\) and either \(b_{0}=0\) for \(f_{0}(t)>0\) or \(b_{0}= \pi \) for \(f_{0}(t)<0\). This extended model also satisfies the assertion of Theorem 2.1. If we admit beside \((a_{j}, b_{j}) \in (0, \infty ) \times [0, 2\pi )\) also \((a_{j}, b_{j}) = (0,0)\) and \((a_{j}, b_{j}) = (0,\pi )\), the proof of Theorem 2.1 can be suitably modified.
2.2 Classical Fourier coefficients of non-harmonic signals
Now we study the Fourier coefficients of structured functions of the form \(\phi (t) = \gamma \, \cos ( 2\pi a t + b)\) with \(\gamma \in (0, \infty )\), and \((a, \, b) \in (0, \infty ) \times [0, 2\pi ) \) within the interval [0, P) for given \(P>0\).
Theorem 2.3
Let \(\phi (t) = \gamma \, \cos ( 2\pi a t + b)\) with \(\gamma \in (0, \infty )\), \((a, \, b) \in (0, \infty ) \times [0, 2\pi ) \), and let \(P>0\). Then \(\phi \) possesses in [0, P) the Fourier series
with Fourier coefficients \( c_n(\phi ) = \frac{1}{P} \int _0^P \phi (t) \, {\mathrm e}^{-2\pi i n t/P} \, {\mathrm d} t,\) for \(n \in {\mathbb Z},\) where
for \(n \in {\mathbb N}_{0}\), and \(c_{-n}(\phi ) = \overline{c_{n}(\phi )}\). If \(a \in \frac{1}{P} {\mathbb {N}}\), then the Fourier coefficients of \(\phi \) simplify to
Pointwise convergence of the Fourier series for \(\phi (t)\) is given for all \(t \in (0,P)\).
Proof
Since \(\phi (t) = \gamma \, \cos ( 2\pi a t + b)\) is a differentiable function, its restriction onto the interval (0, P) is also differentiable. Thus the Fourier expansion of \(\phi \) converges pointwise for all \(t \in (0, P)\), see [23, Chapter 1]. For the real part of \(c_n(\phi )\) we obtain with \(\cos x \cos y = \frac{1}{2}( \cos (x+y) + \cos (x-y))\)
Assuming that \(a \ne \frac{n}{P}\) it follows with \(\sin x - \sin y = 2 \sin (\frac{x-y}{2} ) \cos (\frac{x+y}{2} ) \)
For \(a = \frac{n}{P}>0\), the function \(\phi \) is P-periodic, and we simply find
This is also achieved from (2.6) by taking the limit with the rule of L’ Hospital,
The formula (2.7) for the imaginary part of \(c_n(\phi )\) can be derived analogously.
Remark 2.4
If \(\phi (t)= \gamma \, \cos (2\pi at + b)\) is constant, i.e., if \(\gamma >0\) and either \((a,b) = (0,0)\) or \((a,b) = (0,\pi )\), then we obtain the Fourier coefficients \(c_{0}(\phi )= \gamma \cos (b)\), and \(c_{n}(\phi ) = 0\) for \(n \in {\mathbb Z} \setminus \{ 0\}\).
2.3 Representation of Fourier coefficients by rational functions
We consider now functions \(f= \sum _{j=1}^{K} f_{j}\) of the form (1.3) with \(f_{j}(t) = \gamma _{j} \cos (2\pi a_{j} t + b_{j})\), \(\gamma _j \in (0, \infty )\) and \((a_j, \, b_{j}) \in (0, \infty ) \times [0, 2\pi )\), where the \(a_{j}\) are assumed to be pairwise distinct. As shown in Theorem 2.3, we have for \(n \in {\mathbb Z}\) and \(a_j \not \in \frac{1}{P} {\mathbb {N}}\) that
where
Note that \(C_{j}\) is real and positive for real values \(a_{j}\). We show that \(A_{j}, \, B_{j},\, C_{j}\), \(j=1, \ldots , K\), completely determine all Fourier coefficients \(c_{n}(f)\) and thus f.
Theorem 2.5
Let f be given as in (1.3) with \(\gamma _{j} \in (0, \infty )\) and \((a_j, \, b_{j}) \in (0, \infty ) \times [0, 2\pi )\). Further let \(a_j \not \in \frac{1}{P} {\mathbb {N}}\) be pairwise distinct. Then, there is a bijection between the parameters \(\gamma _j, \, a_j, \, b_j\), \(j=1, \ldots , K\), determining f(t) and the parameters \(A_j,\, B_j, \, C_j\), \(j=1, \ldots , K\), in (2.9)–(2.11). We have \(C_{j} >0\),
For \(B_{j} \ne 0\),
and \( b_{j} \in [0, \, \pi )\) for \(\mathrm {sign}\Big (A_{j} - B_{j} \sqrt{C_{j}} \cot (\sqrt{C_{j}} \pi ) \Big ) >0\) and \( b_{j} \in [\pi ,\, 2\pi )\) otherwise. Here, \(\mathrm {arccot}\) denotes the inverse cotangens that maps onto \((0, \pi )\). For \(B_{j}=0\), choose \(b_{j}\) from \(\{ -\pi \sqrt{C_{j}} \, \mathrm {mod} \, \pi , -\pi \sqrt{C_{j}} \, \mathrm {mod} \, \pi + \pi \}\) such that (2.10) is satisfied.
Proof
We can assume that \(C_{j} > 0\). Then (2.9) implies that \(a_j= \frac{\sqrt{C_j}}{P} > 0\). Further, taking the weighted sum \(A_{j}^{2} + a_{j}^{2} P^{2} B_{j}^{2}\) using (2.10) and (2.11) we obtain
Since \(\gamma _{j} >0\), we can determine \(\gamma _{j}\) uniquely. Inserting the found representations for \(a_j\) and \(\gamma _j\) into (2.10) and (2.11), we conclude for \(B_{j} \ne 0\)
as well as
and thus \(\mathrm {sign}(A_{j} - B_{j} \,\sqrt{C_{j}} \, \cot (\sqrt{C_{j}} \pi )) = \mathrm {sign} (\sin (b_{j}))\). If \(B_{j}=0\) then \(\sin (a_{j} \pi P + b_{j}) =0\) and thus \(b_{j} \in \{ -\pi \sqrt{C_{j}} \, \mathrm {mod} \, \pi , -\pi \sqrt{C_{j}} \, \mathrm {mod} \, \pi + \pi \}\).
Remark 2.6
1. Since we had assumed that \(a_{j} \not \in \frac{1}{P} {\mathbb {N}}\) and in particular \(a_{j} \ne 0\), it follows that \(C_{j} \ne 0\). As seen from Theorem 2.3, we always have \(C_{j} > 0\) for the considered model. In Sect. 6, we will generalize the model to treat also the case \(C_{j} <0\) which leads to generalized expansions involving also cosine hyperbolic terms.
2. Please note that the function acot used in our Matlab implementation is defined differently, it maps to \([-\pi /2, \pi /2)\).
For f in (1.3) (with \(a_{j} \not \in \frac{1}{P} {\mathbb {N}}\)) we observe with (2.8) that
In particular, the real part \(\text {Re} \, c_n(f)\) and the imaginary part \(\text {Im} \, c_n(f)\) can for all \(n \in {\mathbb Z}\) be written as \( \text {Re} \, c_n(f) = \frac{p^R_{K-1}(n^2)}{q_K(n^2)}\) and \(\text {Im} \, c_n(f) =\frac{n \, p^I_{K-1}(n^2)}{q_K(n^2)}\), where
is a monic polynomial of degree K, and where
is a (complex) algebraic polynomial of degree (at most) \(K-1\). In other words, for \(n \ne 0\),
i.e., the modified Fourier coefficient \(\tilde{c}_{n}(f)\) can be represented by a rational function of type \((K-1,K)\), evaluated at \(z=n^{2}\), where \(q_K(z)\) in (2.13) and \(p_{K-1}(z)\) in (2.14) are coprime.
3 Modified AAA algorithm for sparse signal representation
We want to exploit the special structure of the Fourier coefficients of functions f which are built by function atoms of the form \(f_{j}(t) = \gamma _{j} \, \cos (2 \pi a_{j}t + b_{j})\) in order to study the following problem:
How can we reconstruct a function f of the form (1.3) from a given set of its Fourier coefficients in a numerically stable and efficient way? We assume here that only the structure of f is known, i.e., we need to recover the number K of terms in (1.3) as well as the parameters \(\gamma _{j}, \, a_{j}, b_{j}\) for \(j=1, \ldots , K\).
For the reconstruction process we need to keep in mind that the rational representation of Fourier coefficients in (2.12), or in (2.15) respectively, is only valid for the non-P-periodic terms \(f_{j}\) of f, i.e., for \(a_{j} \not \in \frac{1}{P} {\mathbb {N}}_{0}\). If f contains components \(f_{j}(t)= \gamma _{j} \cos (2 \pi a_{j} t + b_{j})\) with \(a_{j} P = n_{j} \in {\mathbb {N}}_{0}\), then, as shown in Theorem 2.5, these components will provide only one non-zero Fourier coefficient \(c_{n_{j}}(f)\) (with nonnegative index), which destroys the rational function structure (2.15) at \(z=n_{j}^{2}\).
Therefore, our approach consists of two parts. In the first step, we will reconstruct the non-P-periodic part of f, and in a second step, we will determine possible P-periodic terms of f that can be obtained from the set of Fourier coefficients.
To reconstruct the non-P-periodic part of f in (1.3) we will extensively use the structure of the Fourier coefficients \(c_{n}(f)\) found in (2.15) and employ a modification of the recently proposed AAA algorithm in [20]. Differently from other rational interpolation algorithms, the modified AAA algorithm provides essentially higher numerical stability and enables us to determine also the order of the rational approximant which is at the same time the number K of terms in (1.3). The AAA algorithm can be seen as a method for rational approximation, where certain values of a given function are interpolated, while other given values are approximated using a least squares approach. With this algorithm, we will determine the rational function in (2.15) by interpolation or approximation of the given modified Fourier coefficients \(\tilde{c}_{n}(f)\). The algorithm works iteratively, where at each iteration step the degree of the polynomials determining the rational function grows by 1, and a next interpolation value is chosen at the point, where the error of the rational approximation found so far is maximal. The algorithm terminates if either the error at all given points considered for approximation is less than a given bound or if a certain fixed degree of the rational function is reached. If the rational function is found, we can extract the parameters \(A_j, \, B_j, \, C_j\) and then finally obtain the wanted representation with parameters \(\gamma _j, \, a_j, \, b_j\) of the non-P-periodic part of f from Theorem 2.5.
Numerical stability of the AAA algorithm is ensured by a barycentric representation, as already considered in [13, 30] and exploited also in [12], to compute rational minimax approximations. In [20], the AAA-algorithm is presented for rational functions \(r(z) = p(z)/q(z)\), where the polynomials p and q have the same degree. Therefore, we need to modify the approach for our purpose, similarly as proposed in [12]. A side effect of the linearization procedure within the algorithm is that unattainable interpolation points lead to vanishing weight components, see [30]. This behavior of the algorithm enables us to determine possible P-periodic terms of f in a postprocessing step, where we need to inspect all Fourier coefficients that cannot be well approximated by the found rational function.
If f does not contain P-periodic terms and the given Fourier coefficients of f are exact, then we will be able to determine f uniquely from \(2K+1\) Fourier coefficients. This will be shown in Sect. 4. Otherwise, we will need \(2K+2\) Fourier coefficients to recover f, where all P-periodic terms are simply determined in a postprocessing step, see Sect. 5.
3.1 Rational interpolation using barycentric representation
Let us assume now that we are given a set of Fourier coefficients \(c_n(f)\), \(n \in \Gamma \subset {\mathbb {N}}\) of the function f of the form (1.3) with \(L := \# \Gamma \ge 2K+1\). We assume first that all terms of f are non-P-periodic, such that we obtain the rational structure of \(\tilde{c}_{n}= \tilde{c}_{n}(f)\) as given in (2.15). We want to find a rational function \(r_{K}(z) = p_{K-1}(z)/q_{K}(z)\) of type \((K-1, K)\) such that the interpolation conditions
are satisfied. Assuming that the given modified Fourier coefficients \(\tilde{c}_{n}\) of f in (1.3) are exact, we will show in Sect. 4 that \(r_{K}(z)\) will be the wanted rational function in (2.15) that determines f.
As in [13, 17, 20], we will use the barycentric representation of \(r_{K}(z) = \tilde{p}_{K}(z)/\tilde{q}_{K}(z)\) with
where \(w_j\), \(j=1, \ldots , K+1\), are nonzero weights, and where \(n_{j} \in \Gamma \) for \(j=1, \ldots , K+1\). Here, \(n_{j}^{2}\), \(j=1, \ldots , K+1\), cannot occur as poles of \(r_{K}(z)\), since the poles \(C_{j}\) in (2.13) satisfy \(C_{j}= a_{j}^{2} P^{2} \not \in {\mathbb {N}}\) by assumption. It can be simply observed that \(\tilde{p}_{K}(z)/\tilde{q}_{K}(z)\) is indeed a rational function of type (K, K). In order to ensure that \(r_{K}(z)\) is of the wanted type \((K-1,K)\), we require the additional condition \(\sum _{j=1}^{K+1} w_{j} \, \tilde{c}_{n_{j}} =0\).
The representation (3.1) already incorporates the interpolation conditions \(r_{K}(n_{k}^{2}) = \tilde{c}_{n_{k}}(f)\), for \(k=1, \ldots , K+1\), since we have for \(w_{k} \ne 0\)
Let \(S_{K+1} :=\{n_{1}, \ldots , n_{K+1}\}\) be the index set, where for nonzero weights \(w_{k}\) the interpolation conditions are already satisfied. To determine \(r_{K}(z)\) using (3.1) we still need to fix the normalized weight vector \({\mathbf{w}}=(w_{1}, \ldots , w_{K+1})^{T}\). According to [20], this is done by solving a least squares problem in order to minimize the error
where beside \(\Vert {\mathbf{w}} \Vert _{2} =1\), in our case we will incorporate the side condition \(\sum _{j=1}^{K+1} w_{j} \, \tilde{c}_{n_{j}} =0\) to ensure that \(r_{K}(z)\) is of type \((K-1,K)\). The algorithm is described in the next two sections and closely follows the approach in [20] with the modification that we want to get a rational function of type \((K-1,K)\) instead of type (K, K).
3.2 Initialization of the modified AAA algorithm
We start by initializing the modified AAA-algorithm as follows. First, we choose the two given modified Fourier coefficients \(\tilde{c}_{n_1}\), \(\tilde{c}_{n_2}\) with largest modulus (where \(n_1 \ne n_2\) and \(n_1, \, n_2 \in \Gamma \)) for interpolation and compute a rational function \(r_{1}(z)\) of type (0, 1) that interpolates \(\tilde{c}_{n_1}\) at \(z=n_{1}^{2}\) and \(\tilde{c}_{n_2}\) at \(z=n_{2}^{2}\). We determine the rational function
such that \(r_1(n_1^2) = \tilde{c}_{n_1}\) and \(r_1(n_2^2) = \tilde{c}_{n_2}\) holds. A barycentric form of \(r_1(z)\) as in (3.1) is given by
with the (complex) weights
satisfying \(|w_1|^2+|w_2|^2=1\) and \(w_1 \tilde{c}_{n_1} + w_2 \tilde{c}_{n_2} =0\). Obviously, \(\tilde{p}_{1}(z)\) and \(\tilde{q}_{1}(z)\) are themselves rational functions of type (at most) (1, 2). The condition \(w_1 \tilde{c}_{n_1} + w_2 \tilde{c}_{n_2} =0\) ensures that the polynomial
is only constant (and not linear).
In order to decide, which interpolation point should be taken at the next iteration step, we consider the error \(|r_1(n^2) - \tilde{c}_n|\) for all \(n \in \Gamma \setminus \{ n_{1}, n_{2}\}\). Following the lines of [20], we use the notation \(S_2:= \{n_1, \, n_2 \} \subset \Gamma \) and \(\Gamma _{2}: = \Gamma \setminus S_2\). Let the Cauchy matrix \({\mathbf{C}}_2\) be given by \( {\mathbf{C}}_2 := \left( \frac{1}{n^2-n_j^2}\right) _{n \in \Gamma _{2}, n_j \in S_{2}} \) with 2 columns and \(L-2\) rows. Then the vectors of function values \(\left( \tilde{p}_1(n^2) \right) _{n \in \Gamma _{2}}\) and \(\left( \tilde{q}_1(n^2) \right) _{n \in \Gamma _{2}}\) satisfy
and \(\max \nolimits _{n \in \Gamma _{2}} |r_1(n^2) - \tilde{c}_n| = \max \nolimits _{n \in \Gamma _{2}} |\tilde{p}_{1}(n^2)/\tilde{q}_{1}(n^{2}) - \tilde{c}_n|\) can be easily computed. We choose \({{n_3}} = \mathop {\mathrm {argmax}}\nolimits _{n \in \Gamma _{2}} |r_1(n^2) - \tilde{c}_n|\) as the next index for interpolation and set \(S_3:= S_2 \cup \{ {{n_3}}\}\) and \(\Gamma _{3}:= \Gamma _{2} \setminus \{{{ n_3}} \}\).
3.3 General iteration step of the modified AAA algorithm
At step \((J-1)>1\), assume that we have given the index set \(S_{J}:=\{n_1, \ldots , n_{J}\} \subset \Gamma \), where we want to interpolate, and let \(\Gamma _{J} := \Gamma \setminus S_{J}\). Further, let
be the given vectors of (modified) Fourier coefficients as in (2.15), where we will take \(\tilde{\mathbf{c}}_{S_{J}}\) for interpolation and \(\tilde{\mathbf{c}}_{\Gamma _{J}}\) for approximation.
We use a barycentric representation as in (3.1) and start with the ansatz \(r_{J-1}(z) = \tilde{p}_{J-1}(z)/\tilde{q}_{J-1}(z)\) with
and weights \(w_j\), \(j=1, \ldots , J\). Then \(r_{J-1}(z)\) already satisfies the interpolation conditions \(r_{J-1}(n_j^2) = \tilde{c}_{n_j}\) for \(w_{j} \ne 0\). The vector of weights \({\mathbf{w}} := (w_1, \ldots , w_J)^T\) has still to be chosen suitably with the side conditions
to ensure that \(r_{J-1}(z)\) is of type \((J-2, J-1)\). As in the original AAA algorithm, the remaining freedom to choose \({\mathbf{w}}\) is now used in order to approximate the (modified) Fourier coefficients \(\tilde{c}_n\) by \(r_{J-1}(n^2)\) for \(n \in \Gamma _{J}\) applying a (linearized) least squares approach. Observing that \(r_{J-1}(z) \tilde{q}_{J-1}(z) = \tilde{p}_{J-1}(z)\), we consider the minimization problem
Similarly to [20], we define the matrices
Then we can write
such that the minimization problem in (3.5) takes the form
To solve the minimization problem (3.7) approximatively, we compute the right (normalized) singular vectors \({\mathbf{v}}_1\) and \({\mathbf{v}}_2\) of \({\mathbf{A}}_J\) corresponding to the two smallest singular values \(\sigma _{1} \le \sigma _{2}\) of \({\mathbf{A}}_J\) and take a linear combination \({\mathbf{w}}_{J} = \mu _1 {\mathbf{v}}_1 + \mu _2 {\mathbf{v}}_2\) such that \(\Vert {\mathbf{w}}_{J}\Vert _2=1\) and \({\mathbf{w}}_{J}^T \tilde{\mathbf{c}}_{S_J} =0\). These conditions are satisfied for
Remark 3.1
Obviously, the right singular vector \({\mathbf{v}}_{1}\) already solves \(\mathop {\mathrm {argmin}}\nolimits _{\Vert {\mathbf{w}}\Vert _{2} = 1} \Vert {\mathbf{A}}_{J}\, {\mathbf{w}}\Vert _{2}^{2}\). The vector \({\mathbf{w}}_J\) in (3.8) is a linear combination of the two singular vectors corresponding to the two smallest singular values \(\sigma _{1} \le \sigma _{2}\) of \({\mathbf{A}}_{J}\), such that \(\Vert {\mathbf{A}}_{J} {\mathbf{w}}_{J} \Vert _{2}^{2} \le \sigma _{2}^{2}\). The computed vector \({\mathbf{w}}_{J}\) in (3.8) is optimal if \(\sigma _{1} = \sigma _{2}\) or if \({\mathbf{v}}_{1}^{T} \, \tilde{\mathbf{c}}_{S_{J}} = 0\), i.e., if the singular vector \({\mathbf{v}}_{1}\) to the smallest singular value of \({\mathbf{A}}_{J}\) already satisfies the side condition (3.4), and \({\mathbf{w}}_{J} = {\mathbf{v}}_{1}\). We will show in Sect. 4 that for \(J=K+1\) in case of exact data the matrix \({\mathbf{A}}_{K+1}\) always possesses a kernel vector that solves (3.8).
Having determined the weight vector \({\mathbf{w}}_J\), the rational function \(r_{J-1}\) is completely fixed by (3.3). Now, we consider the errors \(| r_{J-1}(n^2) - \tilde{c}_n|\) for all \(n \in \Gamma _{J}\), where we do not interpolate. The algorithm terminates if \(\max _{n \in \Gamma _{J}} | r_{J-1}(n^2) - \tilde{c}_n| < \epsilon \) for a predetermined bound \(\epsilon \) or if \(J-1\) reaches a predetermined maximal degree. Otherwise, we find the next index for interpolation as
The values \(r_{J-1}(n^2) = \frac{\tilde{p}_{J-1}(n^2)}{\tilde{q}_{J-1}(n^2)}\) can be simply computed by the vectors
as suggested in [20], where \(.*\) indicates pointwise multiplication.
We summarize the modified AAA algorithm to compute the vectors \({\mathbf{w}}_{K+1}\) and the index vector \({\mathbf{S}}_{K+1} :=(n_{1}, \ldots , n_{K+1})^{T}\) determining the rational function \(r_{K}(z) = \frac{p_{K-1}(z)}{q_{K}(z)} = \frac{\tilde{p}_{K}(z)}{\tilde{q}_{K}(z)}\) in (2.15) resp. (3.3) that interpolates the given modified Fourier coefficients \(\tilde{c}_{n}\) if n is a component of \({\mathbf{S}}_{K+1}\), and approximates \(\tilde{c}_{n}\) otherwise.
Algorithm 3.2
(Rational approximation of modified Fourier coefficients by modified AAA)
Input:
\(P>0\) period used for computing the Fourier coefficients
\({\varvec{\Gamma }} \in {\mathbb N}^{L}\) vector of indices of given Fourier coefficients with sufficiently large L
\( {\mathbf{c}} \in {\mathbb C}^{L}\) vector of given Fourier coefficients (corresponding to \(\varvec{\Gamma } \))
\(tol>0\) tolerance for the approximation error (e.g. \(tol = 10^{-10}\))
\(mmax \in {\mathbb N}\) maximal order of polynomials in the rational function
-
Initialization: Build \(\tilde{\mathbf{c}} = \text {Real} ({\mathbf{c}}) + {\mathrm i} \, \text {Imag}({\mathbf{c}})./{\varvec{\Gamma }}\). Initialize the vectors \({\mathbf{S}}= []\), \(\tilde{\mathbf{c}}_{S}=[]\).
-
1.
Find the two components \(\tilde{c}_{n_{1}}\), \(\tilde{c}_{n_{2}}\) of \(\tilde{\mathbf{c}}\) with largest absolute values. Update \({\mathbf{S}},\, \tilde{\mathbf{c}}_{S}, \, {\varvec{\Gamma }}, \, \tilde{\mathbf{c}}\) by adding \(n_{1}\), \(n_{2}\) as components of \({\mathbf{S}}\) and deleting these components in \({\varvec{\Gamma }}\), adding \(\tilde{c}_{n_{1}}\), \(\tilde{c}_{n_{2}}\) in \(\tilde{\mathbf{c}}_{S}\) and deleting them in \(\tilde{\mathbf{c}}\).
-
2.
Compute \({\mathbf{w}} = (w_{1}, w_{2})^{T}\) via (3.2).
-
3.
Compute \({\mathbf{p}} = {\mathbf{C}}_2 \left( \begin{array}{l} w_1 \, \tilde{c}_{n_1} \\ w_2 \, \tilde{c}_{n_2} \end{array} \right) , \; {\mathbf{q}} = {\mathbf{C}}_{2} \left( \begin{array}{l} w_1 \\ w_2 \end{array} \right) \), with \({\mathbf{C}}_{2} = \left( \frac{1}{n^{2} - k^{2}} \right) _{n \in {\mathbf \Gamma }, k \in {\mathbf{S}}}\) and let \({\mathbf{r}} = (r_{j})_{j=1}^{L-2} = {\mathbf{p}} ./ {\mathbf{q}} \in {\mathbb C}^{L-2} \).
-
4.
If \(\Vert {\mathbf{r}} - \tilde{\mathbf{c}}\Vert _{\infty } < tol\) then stop.
-
1.
-
Main Loop for \(m=3:mmax\)
-
1.
Compute \(k = \text {argmax}_{n \in {\varvec{\Gamma }}} | r_{n} - \tilde{c}_{n} |\) and update \({\mathbf{S}},\, \tilde{\mathbf{c}}_{S}, \, {\varvec{\Gamma }}, \, \tilde{\mathbf{c}}\) by adding k as a component of \({\mathbf{S}}\) and deleting it in \({\varvec{\Gamma }}\), adding \(\tilde{c}_{k}\) as a component of \(\tilde{\mathbf{c}}_{S}\) and deleting it in \(\tilde{\mathbf{c}}\).
-
2.
Build the matrices \({\mathbf{C}}_{m} = \left( \frac{1}{n^{2} - k^{2}} \right) _{n \in {\varvec{\Gamma }}, k \in {\mathbf{S}}}\) and \({\mathbf{A}}_{m}= \left( \frac{\tilde{c}_{n} - \tilde{c}_{k}}{n^{2} - k^{2}} \right) _{n \in {\varvec{\Gamma }}, k \in {\mathbf{S}}}\).
-
3.
Compute the normalized right singular vectors \({\mathbf{v}}_{1}\) and \({\mathbf{v}}_{2}\) corresponding to the two smallest singular values of \({\mathbf{A}}_{m}\).
-
4.
Compute \({\mathbf{w}} = ({\mathbf{v}}_{2}^{T} \tilde{\mathbf{c}}_{S}) \, {\mathbf{v}}_{1} - ({\mathbf{v}}_{1}^{T} \tilde{\mathbf{c}}_{S}) \, {\mathbf{v}}_{2}\) and normalize \({\mathbf{w}} = \frac{1}{\Vert {\mathbf{w}}\Vert _{2}} {\mathbf{w}}\).
-
5.
Compute \({\mathbf{p}} = {\mathbf{C}}_m \left( {\mathbf{w}} .* \tilde{\mathbf{c}}_{S} \right) , \; {\mathbf{q}} = {\mathbf{C}}_{m} \, {\mathbf{w}}\), and \({\mathbf{r}} = {\mathbf{p}}./ {\mathbf{q}} \in {\mathbb C}^{L-m}\).
-
6.
If \(\Vert {\mathbf{r}} - \tilde{\mathbf{c}}\Vert _{\infty } < tol\) then stop.
end(for)
-
1.
Output: \(K= m-1, \, {\mathbf{S}} \in {\mathbb N}^{K+1}, \, \tilde{\mathbf{c}}_{S} \in {\mathbb C}^{K+1}, \, {\mathbf{w}} \in {\mathbb C}^{K+1}\), where \({\mathbf{S}}\) is the vector of indices, \(\tilde{\mathbf{c}}_{S}\) the corresponding coefficient vector of interpolation values, and \({\mathbf{w}}\) the weight vector to determine the rational function \(r_{K}\) via (3.3).
As we will show in Sect. 4, it will be sufficient to employ \(L=2K+1\) Fourier coefficients if the function f has no P-periodic components \(f_{j}\). In Sect. 5 we will prove that the algorithm can be also applied if f contains P-periodic terms \(f_{j}\) with frequencies \(a_{j} \in \frac{1}{P}{\mathbb {N}}\). In this case we need \(L=2K+2\) Fourier coefficients, and the rational output function will only determine the Fourier coefficients of the non-periodic part of f. In both cases, for \(L\ge 2K+1\) the Algorithm 3.2 will terminate after K or \(K+1\) iteration steps. Algorithm 3.2 involves SVDs of the matrices \({\mathbf{A}}_{m}\) of size \((L-m) \times m\), \(m=3, \ldots , K+1\) (or \(m=3, \ldots , K+2\)), to compute their singular vectors \({\mathbf{v}}_{1}\) and \({\mathbf{v}}_{2}\) yielding an overall complexity of \({\mathcal O}(L \, K^{3})\) flops, see also [20]. This is modest since K is usually small.
3.4 Partial fraction representation of the rational approximant
Assume that we have found the rational approximant \(r_{K}(z)\) after K iteration steps. In other words, we have now given the vector of interpolation indices \((n_1, \ldots , n_{K+1})^{T}\) and the weight vector \( {\mathbf{w}}_{K+1} = (w_{j})_{j=1}^{K+1} \in {\mathbb C}^{K+1}\), such that
As we will show in Sect. 4, \(r_{K}(z)\) determined by Algorithm 3.2 coincides with the desired rational function in (2.15) for exact data, and, in particular, \(w_{j} \ne 0\) for \(j=1, \ldots , K+1\). To extract the wanted parameters \(A_j\), \(B_j\), and \(C_j\) in (2.12) from \(\{n_1, \ldots , n_{K+1}\}\) and \({\mathbf{w}}_{K+1}\), we need to rephrase \(r_{K}(z)\) in the form
The parameters \(C_j\), \(j=1, \ldots , K\), are the zeros of the rational function \(\tilde{q}_{K}(z)\) in (3.9), since \(z=n_{j}^{2}\) cannot occur as poles of \(r_{K}(z)\) due to the assumption \(C_{j}^{1/2} \not \in {\mathbb {N}}_{0}\), which is by (2.9) equivalent with to \(a_{j} \not \in \frac{1}{P} {\mathbb {N}}_{0}\).
To compute the zeros of \(\tilde{q}_K(z)\) we again draw from the results in [20] or [17] and consider the generalized eigenvalue problem
Observe that \(\lim _{z \rightarrow \pm \infty } \tilde{q}(z) = 0\) causes two infinite eigenvalues that we are not interested in. The other K eigenvalues are the wanted zeros of \(\tilde{q}_K(z)\). This can be simply seen by taking the eigenvectors \({\mathbf{v}}_{\lambda }\) corresponding the eigenvalues \(\lambda \) of the form
such that
Having found the K zeros \(C_j\) of this eigenvalue problem, we obtain from the interpolation conditions \(r_{K}(n_{\ell }^{2}) = \tilde{c}_{n_{\ell }}\) for \(\ell =1, \ldots , K+1\) with (3.10) the linear equation system
in order to determine \(A_{j} + {\mathrm i} B_{j}\), \(j=1, \ldots , K\). We summarize the reconstruction of the parameter vectors \((A_{j})_{j=1}^{K}\), \((B_{j})_{j=1}^{K}\), and \((C_{j})_{j=1}^{K}\) from the output of Algorithm 3.2 in Algorithm 3.3.
Algorithm 3.3
(Reconstruction of parameters \(A_{j}, \, B_{j}, \, C_{j}\) of partial fraction representation)Input: \({\mathbf{S}} \in {\mathbb N}^{K+1}, \, \tilde{\mathbf{c}}_{S} \in {\mathbb C}^{K+1}, \, {\mathbf{w}} \in {\mathbb C}^{K+1}\), the output vectors of Algorithm 3.2
-
1.
Build the matrices in (3.11) and solve this generalized eigenvalue problem to obtain the parameter vector \((C_{1}, \ldots , C_{K})^{T}\) of finite eigenvalues.
-
2.
Build the matrix \({\mathbf{V}} = \left( \frac{1}{n^{2}- C_{j}}\right) _{n \in {\mathbf{S}}, j=1, \ldots , K} \in {\mathbb R}^{(K+1) \times K}\) and solve the linear system
$$ {\mathbf{V}} \, {\mathbf{x}} = \tilde{\mathbf{c}}_{S}. $$Set \((A_{j})_{j=1}^{K} = \text {Real} \, (\mathbf {x})\) and \((B_{j})_{j=1}^{K} = \text {Imag} \, (\mathbf {x})\).
Output: Parameter vectors \((A_{j})_{j=1}^{K}\), \((B_{j})_{j=1}^{K}\), and \((C_{j})_{j=1}^{K}\).
Both steps in Algorithm 3.3 have a complexity of \({\mathcal O}(K^{3})\) flops. Finally, we can reconstruct the wanted parameter vectors \((\gamma _{j})_{j=1}^{K}\), \((a_{j})_{j=1}^{K}\) and \((b_{j})_{j=1}^{K}\) in (1.3) via Theorem 2.5.
4 Exact reconstruction using Algorithm 3.2
Assume that the Fourier coefficients \(c_{n}(f)\) of a function f in (1.3) with K components \(f_j\) are given for \(n \in \Gamma \subset {\mathbb {N}}\) with \(\#\Gamma = L \ge 2K+1\), where we suppose that \(a_j \not \in \frac{1}{P} {\mathbb Z}\) for all components \(f_{j}\) of f. We show that all parameters determining f can be uniquely reconstructed from 2K Fourier coefficients \(c_{n}(f)\) if K is known beforehand. Moreover, if \(L \ge 2K+1\) Fourier coefficients \(c_{n}(f)\) are given, then Algorithm 3.2 terminates after K steps (i.e., taking \(K+1\) interpolation points). Thereby, also K is determined if it is not a priori known.
Theorem 4.1
Let f be of the form (1.3) with \(K \in {\mathbb {N}}\), \(\gamma _{j} \in (0, \infty )\), and \((a_{j}, \, b_{j}) \in (0, \infty ) \times [0, \, 2\pi )\) \(j=1, \ldots , K\). Further, let \(a_{j}\) be pairwise different and \(a_{j}\not \in \frac{1}{P} {\mathbb N}\) for a given \(P>0\). Assume that we have a given set of classical Fourier coefficients \(c_{n}(f)\), \(n \in \Gamma \subset {\mathbb {N}}\) (with regard to period P) with \(L = \# \Gamma \ge 2K+1\). Then f is uniquely determined by 2K of these Fourier coefficients. If \(L\ge 2K+1\), then Algorithm 3.2 terminates after K steps, takes \(K+1\) interpolation points and determines the rational function \(r_{K}(z) = \sum _{j=1}^{K} \frac{A_{j}+ {\mathrm i} B_{j}}{z-C_{j}}\) in (2.15) that interpolates all \(\tilde{c}_{n}(f)\), \(n \in {\mathbb {N}}\), exactly. Moreover, K as well as \(\gamma _{j}\), \(a_{j}\), and \(b_{j}\), \(j=1, \ldots , K\), are uniquely determined by \(r_{K}\).
Proof
1. From (2.15) it follows that there exists a rational function \(r_{K}(z) = \frac{p_{K-1}(z)}{q_{K}(z)}\) of type \((K-1, K)\) such that \(\tilde{c}_{n}= \tilde{c}_{n}(f) = r_{K}(n^{2}) = \frac{p_{K-1}(n^{2})}{q_{K}(n^{2})}\) for all \(n \in {\mathbb {N}}\) with \(q_{K}(z)\) in (2.13) and \(p_{K-1}(z)\) in (2.14). In particular, \(p_{K-1}(z)\) and \(q_{k}(z)\) are coprime.
First, we show that \(r_{K}(z)\) is uniquely determined by 2K coefficients \(\tilde{c}_{n_{j}}(f)\), \(n_{j} \in \Gamma \), \(j=1, \ldots , 2K\). By (2.14), \(p_{K-1}(z)\) has at most degree \(K-1\). Further, \(q_{K}(z)\) has exactly degree K by (2.13). We use the notation \(p_{K-1}(z)= \sum _{r=0}^{K-1} p_{r} z^{r}\) and \({{q_{K}(z)}}= z^{K} + \sum _{r=0}^{K-1}q_{r} \, z^{r}\). Then the interpolation conditions
yield the equation system
This leads to the homogeneous system
with the coefficient matrix
and with \(({\mathbf{p}}^{T}, \, {\mathbf{q}}^{T}) = (p_{0}, \ldots , p_{K-1}, q_{0}, \ldots q_{K-1},1)^{T} \in {\mathbb {R}}^{2K+1}\).
The kernel of \({\mathbf{W}}\) has at least dimension 1, and by construction, the vector \(({\mathbf{p}}^{T}, \, {\mathbf{q}}^{T})\) generating the rational function \(r_{K}(z) = p_{K-1}(z) / q_{K}(z)\) satisfies (4.1). We show that the kernel of \({\mathbf{W}}\) has exactly dimension 1. Suppose to the contrary that there exists another vector in the kernel of \({\mathbf{W}}\) being linearly independent of \(({\mathbf{p}}^{T}, \, {\mathbf{q}}^{T})\). Then we also find a kernel vector, whose last component vanishes, i.e., of the form \( (\breve{\mathbf{p}}^{T}, \, \breve{\mathbf{q}}^{T}) = (\breve{p}_{0}, \ldots , \breve{p}_{K-1}, \breve{q}_{0}, \ldots \breve{q}_{K-2}, \breve{q}_{K-1}, 0)^{T}\). Thus, there exist polynomials \(\breve{p}_{K-1}\) and \(\breve{q}_{K-1}\) of at most degree \(K-1\) satisfying
Using the known structure of \(\tilde{c}_{n_{j}}(f) = p_{K-1}(n_{j}^{2})/q_{K}(n_{j}^{2}) \) in (2.15), we obtain
Since the degree of the involved polynomial products is at most \(2K-1\), it follows that \(\breve{p}_{K-1}(z) \, q_{K}(z) = p_{K-1}(z) \, \breve{q}_{K-1}(z)\) for all \(z \in {\mathbb {R}}\). But \(q_{K}(z)\) is a monic polynomial of degree K and the polynomials \(p_{K-1}(z)\), \(q_{K}(z)\) are coprime, and we conclude that \(\breve{q}_{K-1}(z)\) possesses all K linear factors of \(q_{K}(z)\). This leads to a contradiction, since \(\breve{q}_{K-1}(z)\) has degree at most \(K-1\). Therefore, there exists only one normalized solution vector of the form (4.1), which is already uniquely defined by 2K modified Fourier coefficients of f, and this solution vector \(({\mathbf{p}}^{T}, \, {\mathbf{q}}^{T})^{T}\) determines the rational polynomial \(r_{K}(z) = \frac{p_{K-1}(z)}{q_{K}(z)}\) that satisfies all 2K interpolation conditions.
2. We show now that Algorithm 3.2 leads to this unique solution \(r_{K}(z)\) after K steps. Assume that \(\Gamma \) contains \(L \ge 2K+1\) indices. At the K-th iteration step we have chosen a set \(S_{K+1}\) of \(K+1\) pairwise different indices \(n_{\ell } \in \Gamma \) for interpolation and start with the ansatz
such that the interpolation conditions \(r(n_{\ell }^{2}) = \tilde{c}_{n_{\ell }}\) are already satisfied for \(\ell =1, \ldots , K+1\), if \(w_{\ell } \ne 0\). Let \(\Gamma _{K+1} := \Gamma \setminus S_{K+1}\). Now, Algorithm 3.2 determines the weight vector \({\mathbf{w}}= (w_{\ell })_{\ell =1}^{K+1}\) as a linear combination of the two right singular vectors \({\mathbf{v}}_{1}\) and \({\mathbf{v}}_{2}\) of
corresponding to the two smallest singular values \(\sigma _{1} \le \sigma _{2}\) with side conditions \(\Vert {\mathbf{w}}\Vert _{2} =1\) and \(\sum _{\ell =1}^{K+1} w_{\ell } \tilde{c}_{n_{\ell }} =0\). From (2.12) and (2.15) it follows that
where the two Cauchy matrices have full rank K and where the entries \(-(A_{j} + {\mathrm i} B_{j})\) of the diagonal matrix do not vanish for all \(j=1, \ldots , K\). Thus, \({\mathbf{A}}_{K+1}\) has exactly rank K and therefore a kernel of dimension 1. Let \({\mathbf{v}}_{1}\) be the normalized right singular vector of \({\mathbf{A}}_{K+1}\) to \(\sigma _{1}=0\), i.e., \({\mathbf{A}}_{K+1} {\mathbf{v}}_{1}={\mathbf{0}}\). The factorization of \({\mathbf{A}}_{K+1}\) also implies
We observe that, if \({\mathbf{v}}_{1} \ne {\mathbf{0}}\) had one or more vanishing components, then K columns of the Cauchy matrix \(\left( \frac{1}{n_{\ell }^{2} - C_{j}} \right) _{j=1, \ldots , K, n_{\ell } \in S_{K+1}}\) would be linearly dependent. But this is not possible, since the interpolation points \(n_{\ell } \in S_{K+1}\) are pairwise distinct and therefore any K columns of this Cauchy matrix are linearly independent. Thus, all components of \({\mathbf{v}}_{1}\) are nonzero.
If we determine the rational polynomial r(z) in (4.2) with \({\mathbf{w}}:={\mathbf{v}}_{1}\), then it follows \(r(n_{\ell }^{2}) = \tilde{c}_{n_{\ell }}\) for \(n_{\ell } \in S_{K+1}\) by construction, since all weight components are nonzero. Moreover, the condition \({\mathbf{A}}_{K+1} {\mathbf{w}} = {\mathbf{0}}\) leads to
i.e., it follows that \(r(n^{2}) = \tilde{c}_{n}\) for all \(n \in \Gamma _{K+1}\). Thus, the first part of the proof implies that the obtained rational function r(z) in (4.2) coincides with \(r_{K}(z) = \frac{p_{K-1}(z)}{q_{K}(z)}\) defined by (2.13)–(2.15), and therefore has to be of the wanted type \((K-1, K)\) since it is already uniquely defined by the interpolation conditions. We conclude that \({\mathbf{w}}={\mathbf{v}}_{1}\) already satisfies the side condition \(\sum _{\ell =1}^{K+1} w_{\ell } \tilde{c}_{n_{\ell }} =0\) and is therefore the weight vector computed at the K-th iteration step of Algorithm 3.2.
5 How to proceed if the function contains P-periodic terms
Let us assume that the function \(f(t) = \sum _{j=1}^{K} f_{j}(t)\) is of the form (1.3) with K components \(f_j\), where beside non-periodic components \(f_j(t) = \gamma _{j} \cos (2\pi a_{j} t + b_{j})\) with \(a_j \not \in \frac{1}{P} {\mathbb {N}}\), there are also periodic components with \(a_j \in \frac{1}{P} {\mathbb {N}}\). Now, we will study the question, how Algorithm 3.2 proposed in Sect. 3 behaves in this case and how we can reconstruct f(t).
We assume that the index set \(\Gamma \) of given Fourier coefficients of f contains the integer \(n_j\), if \(a_j = \frac{n_j}{P}\) occurs as a frequency in a component \(f_j\) of f, i.e., \((\{a_{j} P: \, j=1, \ldots , K\} \, \cap \, {\mathbb {N}} ) \subset \Gamma \). Otherwise, the component \(f_j\) cannot be identified from the given data. We assume further that \(L= \# \Gamma \ge 2K+2\). The function f in (1.3) (with the usual restrictions \(\gamma _{j} \in (0, \infty )\), \((a_{j}, \, b_{j}) \in (0, \infty ) \times [0, 2\pi )\)) can now be written as \(f(t)= \phi _{1}(t) + \phi _{2}(t)\), where
is non-P-periodic such that the modified Fourier coefficients \(\tilde{c}_{n}(\phi _{1}) = \mathrm {Re} \, c_{n}(\phi _{1}) + \frac{{\mathrm i}}{n} \, \text {Im} \, c_{n}(\phi _{1})\) are of the form
similarly as in (2.15). The P-periodic part of f(t),
possesses only \(K_{2}:=K-K_{1}\) nonzero Fourier coefficients with non-negative index. Let \(\Sigma :=\{ P \, a_{K_{1}+1}, \ldots , P\, a_{K} \} \subset {\mathbb {N}}\) denote the corresponding index set. Then \(K_{2} = \# \Sigma \), and
Since \(\tilde{c}_{n}(f) = \tilde{c}_{n}(\phi _{1}) + \tilde{c}_{n}(\phi _{2})\) for \(n \in {\mathbb {N}}\), it follows that only \(K_{2}\) modified Fourier coefficients of f are not of the form as in (2.15) while all \(\tilde{c}_{n}(f)\) with \(n \not \in \Sigma \) satisfy \(\tilde{c}_{n}(f) = \tilde{c}_{n}(\phi _{1})\) and can be reconstructed by a rational function of type \((K_{1}-1, K_{1})\). Let us now examine, how to reconstruct f(t) in this setting.
Theorem 5.1
Assume that f(t) is of the form \(f(t) = \phi _{1}(t) + \phi _{2}(t)\) with \(\phi _{1}(t)\) and \(\phi _{2}(t)\) in (5.1) and (5.3), where \(\phi _{2}\) possesses the \(K_{2}\) nonzero Fourier coefficients \(c_{n}(\phi _{2})\), \(n \in \Sigma \subset {\mathbb {N}}\). Assume that we have given a set \({c}_{n}(f)\), \(n \in \Gamma \subset {\mathbb {N}}\) of \(L\ge 2K+2\) Fourier coefficients of f, where the unknown set \(\Sigma \) is contained in \(\Gamma \). Then \(\phi _{1}\) and \(\phi _{2}\), i.e., \(K_{1}, \, K_{2}\) as well as all parameters \(\gamma _{j}, \, a_{j}, \, b_{j}\) determining \(\phi _{1}\) and \(\phi _{2}\) can be completely recovered from this set of Fourier coefficients. In particular, Algorithm 3.2 terminates after at most \(K+1\) steps and provides a rational function \(r_{K_{1}}(z)\) of type \((K_{1}-1,K_{1})\) that interpolates \(\tilde{c}_{n}(f) = \tilde{c}_{n}(\phi _{1})\) for all \(n \in {\mathbb {N}} \setminus \Sigma \).
Proof
Let as before \({{\tilde{c}_{n}(f)}}:= \mathrm {Re} \, c_{n}(f) + \frac{{\mathrm i}}{n} \, \text {Im} \, c_{n}(f)\). Assume that we have taken a set \(S_{K+2} \subset \Gamma \) of \(K+2\) given indices as interpolation points at the \((K+1)\)-th iteration step of Algorithm 3.2. We will show that the matrix \({\mathbf{A}}_{K+2} = \left( \frac{\tilde{c}_{n} - \tilde{c}_{k}}{n^{2} - k^{2}} \right) _{n \in \Gamma _{K+2}, k \in S_{K+2}} \in {\mathbb C}^{L-K-2 \times K+2}\) has rank K and possesses a kernel vector \({\mathbf{w}} \in {\mathbb C}^{K+2}\) that satisfies the side condition \({\mathbf{w}}^{T} \tilde{\mathbf{c}}_{S_{K+2}} = 0\). This in turn will imply that the weight vector \({\mathbf{w}}\) found in Algorithm 3.2 determines the rational function \(r_{K_{1}}(z)\) which interpolates \(\tilde{c}_{n}(\phi _{1})\) for all \(n \in {\mathbb {N}}\).
1. Let \(\Sigma ' \cup \Sigma '' = \Sigma \) with \(\Sigma ' \cap \Sigma '' = \emptyset \) be the partition of \(\Sigma \) such that \(\Sigma ' \subset S_{K+2}\) and \(\Sigma '' \subset \Gamma _{K+2}\), and let \(K_{2}' := \# \Sigma '\) and \(K_{2}'' := \# \Sigma ''\) denote the numbers of elements of \(\Sigma '\) and \(\Sigma ''\), such that \(K_{1}+ K_{2}' + K_{2}'' = K\). Then the \(K+2-K_{2}'\) indices in \(S_{K+2} \setminus \Sigma '\) correspond to modified Fourier coefficients with the rational structure \(\tilde{c}_{n}(f) = \tilde{c}_{n}(\phi _{1}) = \frac{p_{K_{1}-1}(n^{2})}{q_{K_{1}}(n^{2})} = r_{K_{1}}(n^{2})\) as in (5.2), and the same is true for the \(L-K-2-K_{2}''\) indices in \(\Gamma _{K+2} \setminus \Sigma ''\).
Assume that the rows and columns of the matrix \({\mathbf{A}}_{K+2}\) are ordered such that the first \(K+2-K_{2}'\) columns of \({\mathbf{A}}_{K+2}\) correspond to \(S_{K+2}\setminus \Sigma '\), while the last \(K_{2}'\) columns correspond to the index set \(\Sigma '\). Similarly, we suppose that the rows of \({\mathbf{A}}_{K+2}\) are ordered such that the first \(L-K-2-K_{2}''\) rows correspond to the indices \(\Gamma _{K+2} \setminus \Sigma '' \), while the remaining \(K_{2}''\) rows correspond to indices in \(\Sigma ''\). In other words, we obtain
with
Since \({\mathbf{A}}_{11}\) is only composed of the modified Fourier coefficients of the non-periodic function \(\phi _{1}\), it follows similarly as in the proof of Theorem 4.1 that \({\mathbf{A}}_{11}\) possesses rank \(K_{1}\). More exactly, we have with (5.2) the matrix factorization
where the two Cauchy matrices and the diagonal matrix have full rank \(K_{1}\). Therefore, \({\mathbf{A}}_{11}\) possesses a kernel of dimension \(K+2-K_{1}-K_{2}' = K_{2}''+2\). Since \({\mathbf{A}}_{21}\) contains only \(K_{2}'' \le K_{2}\) rows, it follows that \(\left( \begin{array}{ll} \!\! {\mathbf{A}}_{11}\!\!\\ \!\!{\mathbf{A}}_{21} \!\!\end{array} \right) \) has at most rank \(K_{1}+K_{2}''\) and therefore possesses a kernel of dimension at least 2. Thus, \({\mathbf{A}}_{K+2}\) has at most rank \(K_{1}+ K_{2}''+ K_{2}'= K\).
2. We will prove that \({\mathbf{A}}_{K+2}\) has exactly rank K by showing that rank \(({\mathbf{A}}_{11}, {\mathbf{A}}_{12}) = K_{1}+K_{2}'\) and similarly, that rank \(\left( \begin{array}{l} \!\!{\mathbf{A}}_{11} \!\!\\ \!\!{\mathbf{A}}_{21}\!\! \end{array} \right) = K_{1}+K_{2}''\). As in the proof of Theorem 4.1, we can always find a linear combination of \(K_{1}\) columns of \({\mathbf{A}}_{11}\) to represent the columns \(\Big ( \frac{\tilde{c}_{n}(\phi _{1}) - \tilde{c}_{k'}(\phi _{1})}{n^{2} - k'^{2}} \Big )_{n \in \Gamma _{K+2} \setminus \Sigma ''}\) for all \(k' \in \Sigma '\). Indeed for each of these columns we have
where \(\left( \frac{1}{k'^{2}- C_{j}} \right) _{j=1}^{K_{1}}\) can be written as linear combination of the columns in \( \left( \frac{1}{k^{2}- C_{j}} \right) _{j=1, \ldots , K_{1}, k \in S_{K+2} \setminus \Sigma '}\) which generate \({\mathbb {R}}^{K_{1}}\). Thus,
where
and \( \tilde{c}_{k'}(\phi _{2}) \ne 0\) for \(k' \in \Sigma '\). Therefore, it suffices to show that the concatenation of the first matrix factor of \({\mathbf{A}}_{11}\) and \(\left( \frac{1}{n^{2}- k'^{2}} \right) _{n \in \Gamma _{K+2} \setminus \Sigma '', k' \in \Sigma '}\), i.e.,
has full rank \(K_{1}+ K_{2}'\). This is obviously true since this Cauchy matrix has \(L-K-2-K_{2}'' \ge K-K_{2}''=K_{1}+K_{2}'\) rows and the values \(C_{j}\), \(j=1, \ldots , K_{1}\) and \(k'^{2}\), \(k' \in \Sigma '\) are pairwise distinct and also distinct from \(n^{2}\) with \(n \in \Gamma _{K+2}\setminus \Sigma ''\). Similarly we can show that rank \(\left( {\mathbf{A}}_{11}^{T}, \, {\mathbf{A}}_{21}^{T} \right) \) can be simplified to
and has rank \(K_{1}+K_{2}''\).
4. Thus rank \({\mathbf{A}}_{K+2} = K\), i.e., the dimension of the kernel of \({\mathbf{A}}_{K+2}\) is 2. Therefore, Algorithm 3.2 always finds a vector \({\mathbf{w}}\) in the kernel of \({\mathbf{A}}_{K+2}\) which satisfies also the side condition \({\mathbf{w}}^{T} \tilde{\mathbf{c}}_{S_{K+2}} =0\). Moreover, it follows from the previous observations that any vector \({\mathbf{w}}\) in the kernel of \({\mathbf{A}}_{K+2}\), is of the form \( {\mathbf{w}} = (\tilde{\mathbf{w}}^{T}, {\mathbf{0}}^{T}) \in {{ {\mathbb C}^{K+2}}}\), where \(\tilde{\mathbf{w}} \in {\mathbb C}^{K+2-K_{2}'}\) is in the kernel of \(\left( \begin{array}{c} \!\!\!{\mathbf{A}}_{11} \!\!\!\\ \!\!\!{\mathbf{A}}_{21} \!\!\!\end{array} \right) \) and particularly in the kernel of \({\mathbf{A}}_{11}\). Thus, it follows from Theorem 4.1 that \(\tilde{\mathbf{w}}\) has at least \(K_{1}+1\) nonzero components and provides the rational function \(r_{K_{1}}(z)\) that interpolates all modified Fourier coefficients of \(\phi _{1}\). However, differently from the proof of Theorem 4.1, \(\tilde{\mathbf{w}}\) may possess more than \(K_{1}+1\) nonzero components, and the computation of \(r_{K_{1}}(z)\) may involve the removal of Froissart doublets.
5. Having determined \(r_{K_{1}}(z)\) to interpolate all modified Fourier coefficients of \(\phi _{1}\), we can find \(\phi _{2}\) of the form (5.3) by capturing all modified Fourier coefficients \(\tilde{c}_{n}(f)\) with \(\tilde{c}_{n}(f) \ne \tilde{c}_{n}(\phi _{1})\), \(n \in \Gamma \). For all \(n \in \Gamma \), we compute \(\tilde{c}_{n}(\phi _{2}) = \tilde{c}_{n}(f) - r_{K_{1}}(n^{2})\). Then \(\phi _{2}\) can be reconstructed from (5.3) and (5.4), where \(\Sigma \) is found as the set of indices \(n \in \Gamma \) with \(\tilde{c}_{n}(\phi _{2}) \ne 0\), and \(K_{2}= \# \Sigma \).
Remark 5.2
We can also reconstruct \(\tilde{f}(t) = \gamma _{0} + f(t) = \gamma _{0} + \sum _{j=1}^{K} f_{j}(t)\), where \(\gamma _{0} \ne 0\) is a constant. Then \(\gamma _{0}\) can be seen as a periodic component of the function, and we have \(c_{n}(\tilde{f}) = c_{n}(f)\) for all \(n \ne 0\). Thus, if beside the set of Fourier coefficients \(c_{n}(f)\), \(n \in \Sigma \), in Theorem 5.1 also \(c_{0}(\tilde{f})\) is known, then the constant part \(\gamma _{0}\) can be reconstructed, too.
6 Generalization of the model
The model (1.3) for signals considered in the previous sections can be generalized. Beside \((a_{j}, \, b_{j}) \in (0, \infty ) \times [0, \, 2\pi )\) we now admit \( (a_{j}, \, b_{j}) \in {\mathrm i} (0, \infty ) \times {\mathrm i} {\mathbb {R}}\) for \(j \in \{1, \ldots , K\}\), i.e., the parameters \(a_{j}\) and \(b_{j}\) are complex with vanishing real part. Observing that \(\cos ({\mathrm i} (2\pi a t + b) ) = \cosh (2\pi a t + b)\) for real numbers \(a, \, b\), we can consider the generalized function model
where \(\kappa \in \{1, \ldots , K\}\), \(\gamma _j \in (0, \infty )\) for \(j=1, \ldots , K\), and \((a_j, \, b_{j}) \in (0, \infty ) \times [0, 2\pi )\) for \(j=1, \ldots , \kappa \), as well as \(\tilde{a}_{j}= -{\mathrm i} \, a_{j} \in (0, \infty )\), \(\tilde{b}_{j} = -{\mathrm i} \, b_{j}\in {\mathbb {R}}\) for \(j=\kappa +1, \ldots , K\). Here, we assume as before that \(a_{j}\), \(j=1,\ldots K\), are pairwise distinct. Model (1.3) is obtained from (6.1) for \(\kappa =K\). In particular, we obtain similarly to Theorem 2.1 the uniqueness of the parameter representation of f in (6.1).
Corollary 6.1
Let f be given as in (6.1) with \(K\in {\mathbb {N}}\), \(\gamma _j \in (0, \infty )\), and \((a_j , \, b_j) \in (0, \infty ) \times [0, 2\pi )\), or \((a_j , \, b_j) \in {\mathrm i} (0, \, \infty ) \times {\mathrm i} {\mathbb {R}}\), where \(a_{j}\) are pairwise distinct. Further, let
with \(M \in {\mathbb {N}}\), \(\delta _j \in (0, \infty )\), and \((c_j , \, d_j) \in (0, \infty ) \times [0, 2\pi )\) or \((c_j , \, d_j) \in {\mathrm i} (0, \, \infty ) \times {\mathrm i} {\mathbb {R}}\), where \(c_{j}\), \(j=1, \ldots , M\), are pairwise distinct. If \(f(t) = g(t)\) for all t on an interval \(T \subset {\mathbb {R}}\) of positive length, then we have \(K=M\) and (after suitable permutation of the summands) \(\gamma _{j}=\delta _{j}\), \(a_{j}=c_{j}\), \(b_{j}= d_{j}\) for \(j=1, \ldots , K\).
Corollary 6.1 can be proved analogously to Theorem 2.1, using that for \(x \in {\mathbb {R}}\) we have \(\cos ( {\mathrm i} \, x) = \cosh x\) and \(\sin ({\mathrm i} \, x) = {\mathrm i} \, \sinh x\), where \(\sinh \) is an odd function with only one zero \(x=0\). Moreover, we can generalize Theorem 2.3.
Corollary 6.2
Let \(\phi (t) = \gamma \cos (2\pi {a} + {b}) = \gamma \cosh ((-{\mathrm i} (2\pi {a} t + {b}))\) for \((a, \, b) \in {\mathrm i} (0, \, \infty ) \times {\mathrm i} {\mathbb {R}}\), and \(P>0\). Then \(\phi \) possesses the Fourier series \(\phi (t) = \sum \nolimits _{n \in {\mathbb Z}} c_{n}(\phi ) \, {\mathrm e}^{2\pi {\mathrm i} nt/P}\) with
In particular, the Fourier coefficients \(c_{n}(\phi )\) do not vanish for all \(n \in {\mathbb {N}}\).
Thus, the Fourier coefficients of the signal in model (6.1) have still the same structure as found for the model (1.3) in Sect. 2.3. More precisely, for \(f_{j}(t) = \gamma _{j}\cos (2\pi a_{j} t + b_{j})\) with \((a_{j}, \, b_{j}) \in {\mathrm i} (0, \, \infty ) \times {\mathrm i} {\mathbb {R}}\), we also have
with
Hence, the obtained parameters \(A_{j}\), \(B_{j}\), \(C_{j}\) have exactly the same form as in (2.9)–(2.11). Moreover, we can reconstruct the parameters \(\gamma _{j}, \, a_{j}, \, b_{j}\) of f in (6.1) from \(A_{j}\), \(B_{j}\), \(C_{j}\) via a generalization of Theorem 2.5.
Corollary 6.3
Let f(t) be given as in (6.1) with \(\gamma _{j} \in (0, \infty )\) and with either \((a_j, \, b_{j}) \in (0, \infty ) \times [0, \, 2\pi )\) with \(a_{j} \not \in \frac{1}{P}{\mathbb {N}}\) or \((a_j, \, b_{j}) \in {\mathrm i} (0, \infty ) \times {\mathrm i} {\mathbb {R}}\). Then, there is a bijection between the parameters \(\gamma _j, \, a_j, \, b_j\), \(j=1, \ldots , K\), determining f(t) and the parameters \(A_j,\, B_j, \, C_j\) in (2.9)–(2.11), for \(j=1, \ldots , K\). For \(C_{j} >0\) we obtain \(a_{j}, \, \gamma _{j}, \, b_{j}\) via Theorem 2.5. For \(C_{j} < 0\), we find
Proof
For \(C_{j} < 0\) it follows that \(a_j= \text {i} \frac{\sqrt{|C_j|}}{P}\). Further, we obtain
The parameter \(\gamma _{j}>0\) is thus uniquely defined, since we always have \(A_{j}^{2} + C_{j} B_{j}^{2} >0\). Finally, inserting the found parameters \(\gamma _{j}\) and \(a_{j}\) into (2.10) and (2.11), we obtain
and \( \text {sign} (\sqrt{|C_{j}|} \pi - {\mathrm i} b_{j}) = \text {sign} \, B_{j}\), where \(\mathrm {arccosh}\) is the inverse of \(\cosh \) and maps onto \([0,\infty )\). Note that for \(C_{j} <0\), we necessarily have \(A_{j} >0\).
Therefore, Algorithm 3.2 can also be applied to a set of Fourier coefficients of the generalized model (6.1) to obtain a rational function that approximates the Fourier coefficients of the non-periodic part of f. Then, we apply Algorithm 3.3 as before to find the partial fraction decomposition of the rational function as described in Sect. 3.4, and can reconstruct the wanted parameters for the nonperiodic part of f in (6.1) using Corollary 6.3. Finally, if f contains a periodic part \(\phi _{2}\) as studied in Sect. 5, i.e., if there are parameters \(a_{j} \in \frac{1}{P} {\mathbb {N}}\), then \(\phi _{2}\) can be reconstructed via Theorem 5.1.
Remark 6.4
The model (6.1) for real non-periodic functions f is the most general model, such that Fourier coefficients of f can be written as in (2.12). In particular, complex values for \(C_{j}\) cannot occur in (2.12) for real functions, since we always have \(c_{-n}(f) = \overline{c_{n}(f)} \) for \(n \in {\mathbb {N}}\).
7 Numerical experiments
In this section we present two numerical experiments, which show that the considered reconstruction scheme provides very good reconstruction results even for small frequency gaps, if P is chosen suitably. We will compare our results for parameter reconstruction with the ESPRIT method/matrix pencil method (a stabilized variant of Prony’s method) as it is for example summarized in [25, Section 3], see also [10, 27]. We remark that a direct comparison of our method with Prony-like methods is difficult, since these methods require different input values. Our model (1.3) can be rewritten as an exponential sum of the form
where
For the matrix pencil method we will employ equidistant function samples f(hk), \(k=1, \ldots , L\), \(L \ge 4K\). To choose a suitable step size h, we need to assume that a good estimate of the upper bound of occurring frequencies is known beforehand, since we need to take \(h^{-1} > \max \{ 2 \,a_{j}: \, j=1, \ldots , K\}\) to avoid aliasing. In this way we ensure that \(2 \pi \lambda _{j}h\) is in \([-\pi , \pi )\) such that \(\lambda _{j}\) can be uniquely determined from \({\mathrm e}^{2\pi {\mathrm i} \lambda _{j} h}\).
Since all parameters \(\gamma _{j}\), \(b_{j}\), \(a_{j}\), \(j=1, \ldots , K\), can already be reconstructed from the shorter exponential sum
we will also apply the matrix pencil method to the equidistant function samples \(\tilde{f}(hk)\), \(k=1, \ldots , L\), \(L \ge 2K\). Further, for the application of Prony’s method, we will take 2K (or K) as a known parameter in the matrix pencil algorithm, while our new method will detect the parameter K itself.
In the first example, we start with the signal from [6],
According to our model (1.3), f(t) is given by the parameter vectors
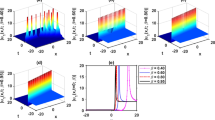
In [6], this function has been considered in the interval [0, 20). But in this interval already 4 of the 6 terms are periodic. We consider f(t) first in the interval [0, 4), i.e., we take \(P=4\), see Fig. 1 (left). Then, the signal has a periodic part \(\phi _{2}(t) = \cos (2\pi (5 t)) + 2 \cos (2\pi t)\), while \(\phi _{1}(t) = \cos (2\pi (4.9t)) + \cos (2\pi (0.96t)) + \cos (2\pi (0.92t)) +\cos (2\pi (0.9t))\) is non-P-periodic. We want to reconstruct f(t) using the Fourier coefficients \(c_{n}(f)\) for \(n=1, \ldots , 20\). We apply Algorithm 3.2 with \(tol=10^{-13}\).
Algorithm 3.2 starts with the initialization values of largest magnitude \(c_{4}(f)\), \(c_{20}(f)\). Then the algorithm takes the further interpolation points \(c_{3}(f)\), \(c_{19}(f)\), \(c_{5}(f)\), \(c_{18}(f)\), \(c_{1}(f)\) (in this order) before it stops after 6 iteration steps with error \(3.9 \cdot 10^{-17}\). The first two terms of \({\mathbf{w}} \in {\mathbb C}^{7}\) vanish, indicating that \(c_{4}(f)\) and \(c_{20}(f)\) are not interpolated by the obtained rational function r(z). Indeed, for \(a_{1}=5\) and \(a_{3}=1\), we have that \(a_{1}P = 20\) and \(a_{3}P = 4\) are integers and therefore \(c_{20}(f)\) and \(c_{4}(f)\) contain information about the periodic part of f(t). After omitting these two terms in \({\mathbf{w}}\) and in the corresponding index vector \({\mathbf{S}}\), we get r(z) of order (3, 4) of the form (3.1) with
Having found r(z), the parameters of the non-P-periodic part \(\phi _{1}(t)\) are reconstructed from r(z) via Algorithm 3.3 and Theorem 2.5. The periodic part \(\phi _{2}(t)\) of f(t) is now determined according to Theorem 5.1 using (5.4). All parameters can be recovered with high precision, where
where \(\tilde{\mathbf{a}}\), \(\tilde{\mathbf{b}}\) and \(\tilde{{\varvec{\gamma }}}\) are the reconstructed parameter vectors.
Taking the same setting with \(L=40\) Fourier coefficients \(c_{n}(f)\), \(n=1, \ldots , 40\), the algorithm chooses the interpolation values \(c_{4}(f)\), \(c_{20}(f)\) for initialization, and then \(c_{3}(f)\), \(c_{22}(f)\), \(c_{5}(f)\), \(c_{19}(f)\), \(c_{1}(f)\) in this order before terminating with error \(1.11 \cdot 10^{-16}\). In this case the parameters are reconstructed with errors
We consider the same example for period \(P=8\) and for given Fourier coefficients \(c_{n}(f)\), \(n=1, \ldots , 40\), see Fig. 1 (right). In this case the algorithm starts with the initial values \(c_{8}(f)\), \(c_{7}(f)\) and then takes iteratively the interpolation values \(c_{9}(f)\), \(c_{40}(f)\), \(c_{39}(f)\), \(c_{38}(f)\) and \(c_{6}(f)\), before terminating with error \(1.8 \cdot 10^{-16}\). The first and the 4th component of the vector \({\mathbf{w}} \in {\mathbb C}^{7}\) vanish and are removed. These components are related to the periodic part \(\phi _{2}(t)\), since \(a_{1}P = 40\) and \(a_{3}P = 8\). We obtain a rational function r(z) of type (3, 4) given via (3.1) with
The rational function r(z) determines \(\phi _{1}(t)\). Afterwards, \(\phi _{2}(t)\) is reconstructed by Theorem 5.1 and (5.4). The parameter vectors are recovered by the algorithm with errors
For comparison, we apply the matrix pencil method, see [10, 25, 27]. Taking the function values f(kh), \(k=1, \ldots , L\), with \(h=0.09\) (since we need \(h<0.1\) to avoid aliasing) and a priori known value \(2K=12\), we obtain for \(L=40\), \(L=80\) and \(L=100\) the errors in Table 1. Analogously, application of the matrix pencil method to function values \(\tilde{f}(kh)\), \(k=1, \ldots , L\), of \(\tilde{f}\) as in (7.2) with \(h=0.09\) and given \(K=6\) yields the errors in Table 2. Larger numbers L of function values do not lead to better recovery results. The occurring difficulties of Prony-like methods to recover the parameters with higher precision are due to the small gaps between frequencies on the one hand and the need to take small step size h on the other hand. Improved recovery results could be obtained in this case by applying a special treatment, where aliasing is exploited, see [7].
In a second example we consider the function
i.e., f(t) is given by the parameter vectors
Plot of f(t) in (7.4) on [0, 1] and on [0, 4]
Taking \(P=1\), this function has a periodic part \(\phi _{2}(t)=\cos (2\pi (4t)+0.2)\), while \(\phi _{1}(t)\) consists of the other five non-1-periodic terms, see Fig. 2. We employ 40 Fourier coefficients \(c_{n}(f)\), \(n=1, \ldots , 40\), for the recovery of f. Algorithm 3.2 finds the values \(c_{2}(f)\) and \(c_{1}(f)\) for initialization. At the next iterations steps the values \(c_{6}(f)\), \(c_{5}(f)\), \(c_{9}(f)\), \(c_{10}(f)\), \(c_{40}(f)\), \(c_{4}(f)\), are taken for interpolation before the algorithm terminates with error \(5.59 \cdot 10^{-17}\) after 7 iteration steps. The last component of \({\mathbf{w}} \in {\mathbb C}^{8}\) (which is related to the periodic part of f since \(a_{4} P = 4\)) is vanishing and will be skipped. We get a rational function r(z) of type (5, 6), determined by (3.1) via
One Froissart doublet occurs in r(z). This is due to the fact that the Fourier coefficient \(c_{4}\) corresponding to the periodic part of f has been chosen for interpolation by Algorithm 3.2 only in the last iteration step. According to the proof of Theorem 5.1, we therefore need 7 iteration steps to generate a kernel of \({\mathbf{A}}_{8}\) of dimension 2. Application of Algorithm 3.3 then leads to 6 finite eigenvalues \(C_{1}, \ldots ,C_{6}\) of (3.11), while the equation system at the second step of Algorithm 3.3 yields a vector \((A_{j} + {\mathrm i} B_{j})_{j=1}^{6}\) with one vanishing component. This component and the corresponding component \(C_{j}\) (which is in \({\mathbb {N}}\) up to numerical error) are removed to obtain the rational function of type (4, 5) determining the non-periodic part \(\phi _{1}\) of f. We reconstruct the parameter vectors \(\tilde{\mathbf{a}}\), \(\tilde{\mathbf{b}}\) and \(\tilde{\varvec{\gamma }}\) according to Theorem 2.5 and Theorem 5.1 with (5.4) and errors
For comparison, the matrix pencil method applied to function values f(kh) with \(h=0.05\) (since we need \(h^{-1} > 2\sqrt{89}\) to avoid aliasing) and \(k=1, \ldots , L\) leads here also to very good recovery results since in this case, we have no small frequency gaps, and Prony’s method does not need to care for frequency parameters being close to \(\frac{1}{P} {\mathbb Z}\). We obtain for f in (7.4) and the corresponding function \(\tilde{f}\) the results in Tables 3 and 4. One needs to keep in mind here that the almost optimal step size \(h=0.05\) has been taken here, which needs a priori knowledge about the size of the maximal frequency. Already \(h=0.04\) and \(L=80\) gives for the recovery of f only the errors \(\Vert {\mathbf{a}} - \tilde{\mathbf{a}} \Vert _{\infty }= 2.90\cdot 10^{-11}\) instead of \({1.57}\cdot 10^{-14}\), \(\Vert {\mathbf{b}} - \tilde{\mathbf{b}} \Vert _{\infty } = 3.12\cdot 10^{-10}\) instead of \({1.97}\cdot 10^{-13}\), and \(\Vert {{\varvec{\gamma }}} - \tilde{{\varvec{\gamma }}} \Vert _{\infty } = 4.85 \cdot 10^{-10}\) instead of \({5.25}\cdot 10^{-13}\).
8 Conclusions
In this paper we have proposed a new method to recover functions f of the form (1.3) from their Fourier coefficients. This method exploits the special structure of the Fourier coefficients of f on some interval [0, P). More precisely, if all frequencies \(a_{k}\) satisfy \(a_{k} \not \in \frac{1}{P} {\mathbb {N}}\), then \(c_{k}(f)\) can be represented as function values of a special rational function of type \((K-1,K)\). In turn, we can apply an algorithm for rational approximation to recover all Fourier coefficients of f and to reconstruct all parameters \(a_{j}, \, b_{j}\) and \(\gamma _{j}\) determining f. We need however to pay attention if frequency parameters of the form \(\frac{k}{P}\) with \(k \in {\mathbb {N}}\) occur which lead to P-periodic terms in f.
The method in our paper can be generalized to the recovery of extended exponential sums of the form
with \(\gamma _{j,m}, \, \lambda _{j} \in {\mathbb C}\) and \(\gamma _{j,n_{j}} \ne 0\), see [9].
Our method is substantially different from Prony-like methods for the recovery of exponential sums of the form (1.3). In particular, the usual Prony method employs equidistant function values while our method requires the knowledge of Fourier coefficients. The performance of Prony-based algorithms like ESPRIT and matrix pencil method strongly depends on the chosen step size for the input function values. This step size needs to be taken very small if f contains large frequencies. In such cases, only more sophisticated numerical methods that exploit aliasing effects can provide satisfying recovery results, [7]. For our method, no direct knowledge is needed about the highest occurring frequency. Besides the different approach to the recovery of exponential sums that we have taken here, there might be close connections to Prony’s method that still need to be explored.
The numerical stability of our algorithm stems from the numerical stability of the AAA algorithm which is the main ingredient of our method. However, we need to study the numerical stability of this algorithm (in comparison to Prony-like methods) more exactly in the future. In particular, there are two main issues. First, what happens if the gap between neighboring frequencies gets small? Our numerical experiments in [9] show, that the AAA-algorithm still works well while the Prony-like methods break down in this case. Second, how does the algorithm behave for frequencies close to the set \(\frac{1}{P}{\mathbb {N}}\)?
The recovery of parameters of exponential sums from function values (or Fourier coefficients) is an ill-posed problem. Even for small changes in the input data the recovery methods may lead to parameter vectors that are far away from the parameter vectors determining the original signal. This is however not a failure of the recovery method, since the new parameter vectors often lead to exponential sums that approximate the given noisy values better than the exponential sum with the original parameters, see e.g. [34] for examples.
Our future research will focus on the problem of approximation of signals by (short) exponential sums. Signals as in (1.3) can be seen as truly adaptive counterparts of Fourier sums. A general answer to the question, how well smooth functions can be approximated by exponential sums, is open. We are still in need of reliable algorithms to recover digital signals using a small number of structural parameters.
References
Beinert, R., Plonka, G.: Sparse phase retrieval of one-dimensional signals by Prony’s method. Front. Appl. Math. Stat. 3(5), open access (2017)
Berent, J., Dragotti, P.L., Blu, T.: Sampling piecewise sinusoidal signals with finite rate of innovation methods. IEEE Trans. Signal Process. 58(2), 613–625 (2010)
Berg, L.: Lineare Gleichungssysteme mit Bandstruktur und ihr asymptotisches Verhalten. Deutscher Verlag der Wissenschaften, Berlin (1986)
Beylkin, G., Monzón, L.: On approximation of functions by exponential sums. Appl. Comput. Harmon. Anal. 19, 17–48 (2005)
Boßmann, F., Plonka, G., Peter, T., Nemitz, O., Schmitte, T.: Sparse deconvolution methods for ultrasonic NDT. J. Nondestruct. Eval. 31(3), 225–244 (2012)
Chui, C.K., Mhaskar, H.N., van der Walt, M.D.: Data-driven atomic decomposition via frequency extraction of intrinsic mode functions. Int. J. Geomath. 7, 117–146 (2016)
Cuyt, A., Lee, W.-S.: How to get high resolution results from sparse and coarsely sampled data. Appl. Comput. Harmon. Anal. 48(3), 1066–1087 (2020)
Daubechies, I., Lu, J., Wu, H.-T.: Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 30(2), 243–261 (2011)
Derevianko, N., Plonka, G.: Exact reconstruction of extended exponential sums using rational approximation of their Fourier coefficients. arXiv preprint arXiv:2103.07743 (2021)
Fernández Rodríguez, A., de Santiago Rodrigo, L., López Guillén, E., Rodríguez Ascariz, J.M., Miguel Jiménez, J.M., Boquete, L.: Coding Prony’s method in MATLAB and applying it to biomedical signal filtering. BMC Bioinform. 19(451) (2018)
Filbir, F., Mhaskar, H.N., Prestin, J.: On the problem of parameter estimation in exponential sums. Constr. Approx. 35(3), 323–343 (2012)
Filip, S.-I., Nakatsukasa, Y., Trefethen, L.N., Beckermann, B.: Rational minimax approximation via adaptive barycentric representations. SIAM J. Sci. Comput. 40(4), A2427–A2455 (2018)
Floater, M.S., Hormann, K.: Barycentric rational interpolation with no poles and high rates of approximation. Numer. Math. 107, 315–331 (2007)
Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H., Zheng, Q., Yen, N.-C., Tung, C.C., Liu, H.H.: The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 454, 903–995 (1998)
Ionita, A.C., Antoulas, A.C.: Data-driven parametrized model reduction in the Loewner framework. SIAM J. Sci. Comput. 36(3), A984–A1007 (2014)
Kadets, M.I.: The exact value of the Paley–Wiener constant. Dokl. Akad. Nauk SSSR 155(6), 1253–1254 (1964)
Klein, G.: Applications of Linear Barycentric Rational Interpolation. PhD thesis, Fribourg (2012)
Knaepkens, F., Cuyt, A., Lee, W.-S., de Villiers, Dirk I.L.: Regular sparse array direction of arrival estimation in one dimension. IEEE Trans. Antennas Propag. 68(5), 3997–4006 (2020)
Levinson, N.: Gap and Density Theorems. Colloquium Publications. American Mathematical Society, Providence (1940)
Nakatsukasa, Y., Sete, O., Trefethen, L.N.: The AAA algorithm for rational approximation. SIAM J. Sci. Comput. 40(3), A1494–A1522 (2018)
Peter, T., Potts, D., Tasche, M.: Nonlinear approximation by sums of exponentials and translates. SIAM J. Sci. Comput. 33(4), 1920–1947 (2011)
Plonka, G., Pototskaia, V.: Computation of adaptive Fourier series by sparse approximation of exponential sums. J. Fourier Anal. Appl. 25(4), 1580–1608 (2019)
Plonka, G., Potts, D., Steidl, G., Tasche, M.: Numerical Fourier Analysis. Birkhäuser, Basel (2018)
Plonka, G., Stampfer, K., Keller, I.: Reconstruction of stationary and non-stationary signals by the generalized Prony method. Anal. Appl. 17(2), 179–210 (2019)
Plonka, G., Tasche, M.: Prony methods for recovery of structured functions. GAMM Mitt. 37(2), 239–258 (2014)
Potts, D., Tasche, M.: Parameter estimation for exponential sums by approximate Prony method. Signal Process. 90(5), 1631–1642 (2010)
Potts, D., Tasche, M.: Parameter estimation for nonincreasing exponential sums by Prony-like methods. Linear Algebra Appl. 439(4), 1024–1039 (2013)
Qian, T., Wang, Y.-B.: Adaptive Fourier series—a variation of a greedy algorithm. Adv. Comput. Math. 34, 279–293 (2011)
Roy, R., Kailath, T.: ESPRIT estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 37, 984–995 (1989)
Schneider, C., Werner, W.: Some new aspects of rational interpolation. Math. Comput. 47(175), 285–299 (1986)
Vetterli, M., Marziliano, P., Blu, T.: Sampling signals with finite rate of innovation. IEEE Trans. Signal Process. 50(6), 1417–1428 (2002)
Wei, X., Dragotti, P.L.: FRESH-FRI-based single-image super-resolution algorithm. IEEE Trans. Image Process. 25(8), 3723–3735 (2016)
Young, R.M.: An Introduction to Nonharmonic Fourier Series. Academic Press, New York (1980)
Zhang, R., Plonka, G.: Optimal approximation with exponential sums by a maximum likelihood modification of Prony’s method. Adv. Comput. Math. 45(3), 1657–1687 (2019)
Acknowledgements
The authors would like to thank the reviewers for constructive advices to improve the representation of the paper. The authors gratefully acknowledge support by the German Research Foundation in the framework of the RTG 2088.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Communicated by Akram Aldroubi.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Petz, M., Plonka, G. & Derevianko, N. Exact reconstruction of sparse non-harmonic signals from their Fourier coefficients. Sampl. Theory Signal Process. Data Anal. 19, 7 (2021). https://doi.org/10.1007/s43670-021-00007-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43670-021-00007-1
Keywords
- Sparse exponential sums
- Non-harmonic Fourier sums
- Reconstruction of sparse non-periodic signals
- Rational approximation
- AAA algorithm
- Barycentric representation
- Fourier coefficients