Change history
01 January 2022
Due to a font problem some mistakes occurred that have been corrected.
Notes
In Sanskrit or Tamil (Sanskrit: vākya, Tamil: vākkiyam). This volume considers only the Sanskrit ones. The other important class of ephemerides current in Tamil Nadu is the tirukkaṇita pañcāṅkam.
Throughout, page numbers in parentheses refer to the work under review. Here, the authors are quoting K.V. Sarma.
K.V. Sarma, K. Ramasubramanian, M.D. Srinivas and M.S. Sriram, Hindustan Book Agency & Springer, 2008.
K. Ramasubramanian and M. S. Sriram, Hindustan Book Agency & Springer, 2011. The dates for these works are taken from this volume (pp. xxxiii–xxxiv), and the work under review (pp. xxxiv–xxxvii). For a discussion, see the latter, as well as S. Madhavan (Sadratnamālā of Śaṅkara Varman, Kuppuswami Sastri Research Institute, Chennai, 2011), pp. xvii–xxi.
In particular, they have a strong background in Physics.
Presumably Covvaram and not Trichur (xxxii–xxxiii).
Chāndogya Upaniṣad, VIII, 1, VIII, 3.3; Taittīriya Upaniṣad, I, 6.1.
Recall that ko’pi = kaḥ + api, literally “someone”, but that kaḥ is also a name of Brahman. For the early history of the identification of Kaḥ, Prajāpati and Brahman, starting from the interpretations of Ṛgveda X.121, see J. Gonda, Prajāpati’s relations with Brahman, Bṛhaspati and Brahmā, North-Holland, Amsterdam, 1989, especially pp. 61–62 and note 14 on p. 52.
Short for khaṇḍāntyadhruva.
Aryabhaṭīya I.10. See also Brāhmasphuṭasiddḥānta II.2–9, and Mādhava’s improved list of 24 sines given by R.C. Gupta (Gaṇitānanda, edited by K. Ramasubramanian, Springer, 2018, p. 383).
S. Kichenassamy, “Brahmagupta’s apodictic discourse”, Gaṇita Bhāratī, 41:1 (2019) 93–113.
This is not anachronistic so long as one does not assume that Putumana Somayājī used these methods – which the authors do not claim.
Venketeswara Pai R. and M.S. Sriram, “Madhyāhnakālalagna in Karaṇapaddhati of Putumana Somayājī”, Gaṇita Bhāratī, 33:1, (2017) 55–74.
C. Brezinski, History of continued fractions and Padé approximants, Springer, Berlin, 1991. Apparently, a symbolism for continued fractions first appears in a work by Cataldi published in 1613 (see p. 65).
“Rationale of the Chakravala Process of Jayadeva and Bhaskara II”, Historia Mathematica 2 (1975) 167–184. It is conceivable that the theory of continued fractions was eventually an outgrowth of the kuṭṭākāra, but that is a different issue. It is futile to speculate about transmission before the conceptual background of major texts has been ascertained by internal analysis. And so far, this task has only be accomplished for a few propositions.
It could be an outgrowth of the calculus on cords with variable unit, or heterometry, that we have shown to be necessary in order to account for Baudhāyana’s results (S. Kichenassamy, “Baudhāyana’s rule for the quadrature of the circle”, Historia Mathematica, 33:2 (2006), 149–183, http://doi.org/10.1016/j.hm.2005.05.001). Indeed, relations between two ideal cords (without width) already come up in a symmetric fashion: typically, one cord is divided into b parts, of which a make up the other; therefore, it is immediate that the second may be divided into a parts, of which b make up the first.
S. Kichenassamy (2019), op. cit. n. 12. Brahmagupta’s remarkable argument does not seem to have any modern equivalent.
This is a general feature of Indian mathematical exposition, but is also common elsewhere and in fact, seems quite common among innovative works (S. Kichenassamy, “Translating Sanskrit Mathematics”, Aestimatio, N.S. 1, (2020), 183–204 https://ircps.org/aestimatio/aestimatio-ns-volumes/ns-1/183-204/).
The standard phrase is adho’dho sthāpyam. The name vallī does not seem to occur in the earliest treatments, but is is not needed, since the construction of the creeper and its reduction are fully described by this and other phrases.
It would take too long to explain the various ways in which the list of quotients has been used in the Indian literature.
One finds, for \(n\,=\,2, 3, 4, \mathrm{and }5\), \({{Q}_{2}=q}_{1}{ q}_{2}+1\), \({{Q}_{3}=q}_{1}{q}_{2}{q}_{3}+{q}_{1}+{q}_{3}\), \({{Q}_{4}=q}_{1}{q}_{2}{q}_{3}{q}_{4}+{q}_{1}{q}_{2}+{{q}_{1}q}_{4}+{ q}_{3}{q}_{4}+1\) and \({{Q}_{5}= q}_{1}{q}_{2}{q}_{3}{q}_{4}{q}_{5}+{q}_{3}{q}_{4}{q}_{5}+{ q}_{1}{q}_{4}{q}_{5}+{q}_{1}{q}_{2}{q}_{5}+{ q}_{1}{q}_{2}{q}_{3}+{q}_{1} {+ q}_{3}+{q}_{5}\). Although we do not develop this point here for expediency, it is very likely that the result was suggested by the inspection of a number of special cases such as these.
We omit this straightforward, but lengthy verification.
The term dṛggaṇitaikya is already found in Brāhmasphuṭasiddhānta 11.61.
K.A. Nilakantha Sastri, A History of South India, fourth ed., Oxford Univ. Press, 1976, p. 363. He also stresses the existence of other poles of excellence in Kerala: “[t]here were families in Kerala which specialized for generations in particular subjects, like the Thaikkāṭṭu illam in architecture. […] In Āyurveda (medicine) the eight great families […] are well-known” (op. cit., p. 362), and mentions grammarians on pages 363–4. There are stray references to architecture in Yuktibhāṣā.
John Warren (1825), Kala Sankalita: A Collection of Memoirs on the Various Modes according to which the Nations of the Southern Parts of India divide Time: to which are added Three General Tables, wherein may be found by mere inspection the beginning, character, and roots of the Tamul, Tellinga, and Mohammedan Civil Years, concurring, viz. the two former with the European Years of the XVIIth, XVIIlth and XIXth Centuries, and the latter with those from A. D. 622 (A. H. 1) to 1900, Madras, dated Feb. 18, 1825. We omit the details of earlier accounts, from the late eighteenth century.
Charles M. Whish (1834), “On the Hindú Quadrature of the Circle, and the infinite Series of the proportion of the circumference to the diameter exhibited in the four S’ástras, The Tantra Sangraham, Yucti Bhásá, Carana Padhati and Sadratnamála”, Transactions of the Royal Asiatic Society of Great Britain and Ireland, 3(3), 509–523 (read 15th of December, 1832). The passages from Karaṇapaddhati that he quotes (6.5, 6.7) or paraphrases (6.4) are given and discussed in the volume under review on pages 150–154.
H.R. Hoisington,
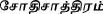 : The Oriental Astronomer, being a Complete System of Hindu Astronomy, accompanied with a translation and numerous notes, with an Appendix. American Mission Press, Jaffna, 1848, in two volumes. It seems to be closely related to the earliest known fully developed form of the system, the Vākyakaraṇa, probably composed in Tamil Nadu between 1282 and 1316. I gather the first and third author plan to edit this work. We mention a different set of vākyas, also in Tamil, in
: The Oriental Astronomer, being a Complete System of Hindu Astronomy, accompanied with a translation and numerous notes, with an Appendix. American Mission Press, Jaffna, 1848, in two volumes. It seems to be closely related to the earliest known fully developed form of the system, the Vākyakaraṇa, probably composed in Tamil Nadu between 1282 and 1316. I gather the first and third author plan to edit this work. We mention a different set of vākyas, also in Tamil, in 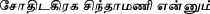
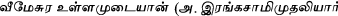 and sons, Chennai, 1939), pages 261–264.
and sons, Chennai, 1939), pages 261–264.For recent progress on measurement, see for instance R. Venketeswara Pai and B.S. Shylaja, “Measurement of coordinates of Nakṣatras in Indian astronomy”, Current Science, 111(9) (10 Nov. 2016), 1551–1558.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kichenassamy, S. Karaṇapaddhati of Putumana Somayājī by Venketeswara Pai, K. Ramasubramanian, M.S. Sriram and M.D. Srinivas, [Hindustan Book Agency, New Delhi and Springer Nature, Singapore, 2018, xlviii + 450 pp., ISBN 978–981-10-6813-3; DOI: 10.1007/978-981-10-6814-0]. Indian J Hist. Sci. 56, 149–153 (2021). https://doi.org/10.1007/s43539-021-00015-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s43539-021-00015-z


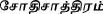 : The Oriental Astronomer, being a Complete System of Hindu Astronomy, accompanied with a translation and numerous notes, with an Appendix. American Mission Press, Jaffna, 1848, in two volumes. It seems to be closely related to the earliest known fully developed form of the system, the Vākyakaraṇa, probably composed in Tamil Nadu between 1282 and 1316. I gather the first and third author plan to edit this work. We mention a different set of vākyas, also in Tamil, in
: The Oriental Astronomer, being a Complete System of Hindu Astronomy, accompanied with a translation and numerous notes, with an Appendix. American Mission Press, Jaffna, 1848, in two volumes. It seems to be closely related to the earliest known fully developed form of the system, the Vākyakaraṇa, probably composed in Tamil Nadu between 1282 and 1316. I gather the first and third author plan to edit this work. We mention a different set of vākyas, also in Tamil, in 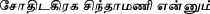
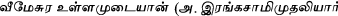 and sons, Chennai, 1939), pages 261–264.
and sons, Chennai, 1939), pages 261–264.