Abstract
This study investigates how regional business cycles are spatially dependent in Mexico by developing a Markov switching model with a spatial autoregressive process. The Markov switching model with two regimes distinguishes business cycles between expansion and recession phases (i.e., high- and low-growth rate regimes). The objective of this study is twofold. First, this study aims to identify which states transitioned from expansion to recession during the Great Recession in 2008–2009. Second, it numerically examines the extent to which states that experienced this transition caused a deterioration in neighboring states’ economies. Employing Bayesian inference for the Markov switching model with quarterly data of state economic activity during the period 2003:Q1–2015:Q4, this study finds that Mexican states with higher manufacturing sector shares tended to be in recession during the Great Recession. Although some states experienced economic downturns in this period, they were not in a recessionary regime. This study also finds that business cycles across states were spatially dependent during the Great Recession. The numerical simulations of spatial spillover effects suggest that states that regime-switched from expansion to recession during the Great Recession caused a reduction in the quarterly growth rate of their neighboring economies by an average of 0.39 percentage points.





Similar content being viewed by others
Availability of data and material
The data are available upon request.
Code availability
The Ox codes are available upon request.
Notes
The approach of Hamilton and Owyang (2012) can identify regional common factors of business cycles within a Markov switching model. Another major approach to regional business cycles is to estimate a dynamic factor model. For example, see Kose et al. (2003), Owyang et al. (2009), and Hirata et al. (2013).
Note that business cycles should involve co-movement of a wide range of economic activities such as output, employment, and sales (Stock and Watson, 1989). Following Burns and Mitchell (1946), as emphasized by Stock and Watson (1989), it is imprecise to define business cycles only in terms of fluctuations in either GDP or employment. Nevertheless, a Markov switching model that uses GDP growth rates provides insights into business cycles by estimating unobservable expansionary and recessionary regimes.
Delajara (2011) investigated co-movement across Mexican states during the recession period of 2008–2009. He suggested the possibility of geographical propagation, although he did not provide direct evidence. This study provides the evidence to support his discussion.
To the best of my knowledge, Ohtsuka (2010) is the first to introduce a spatial autoregressive process into a standard Markov switching model, discovering that business cycles across Japanese regions are spatially dependent.
An MCMC estimation methodology for a Markov switching model was first suggested by Albert and Chib (1993). However, there were questions related to how discrete, hidden variables ought to be sampled. By developing the single-move Gibbs sampling initially proposed by Albert and Chib (1993), Kim and Nelson (1998, 1999a, b) improved sampling efficiency by using multi-move Gibbs sampling for hidden variables. In the literature on regional business cycles, Owyang et al. (2005) and Owyang et al. (2008) also adopted the method proposed by Kim and Nelson (1998, 1999a, b) for model estimation.
Although this study assumes normally distributed errors, the mixture of normals may be appropriate when the error distribution is unknown. Hwu and Kim (2020) provide comparison between models with different assumptions in the context of the Markov-switching model.
The sufficient condition of the stability of the model (2) requires \(\left|{\rho +\phi }_{n}\right|<1 \; \mathrm{and} \; \rho \in \left(-1, 1\right)\) for \(n=1, 2,\ldots,N\), when the SWM is row-standardized (e.g., Yu et al. 2008; Debarsay et al. 2012; Han and Lee 2016). Note that all the eigenvalues of \(\boldsymbol{W}\) are less than or equal to 1 in absolute term when the SWM is row-standardized (Yu et al. 2008). In addition, the parameter \(\rho\) is a unique parameter to be estimated for the spatial dependence. Although researchers are originally interested in an \(N\times N\) coefficient matrix for spatial dependence across regions, it is hard to empirically estimate all coefficient parameters. Therefore, the spatial dependence is reduced to \(\rho \boldsymbol{W}\), where the SWM \(\boldsymbol{W}\) is ex-ante given by researchers, and the parameter \(\rho\) represents the strength of the spatial dependence in the entire economy. An advanced approach is proposed by Aquaro et al. (2021), in which heterogeneous spatial lag coefficients \({\rho }_{n}\) (\(n=1,2,\ldots,N\)) are considered in spatial panel models (see also Autanto-Bernard and LeSage 2019). Another extension of the regional Markov-switching model is including the spatial lag of the lagged dependent variable \({\boldsymbol{W}}{\boldsymbol{y}}_{t-1}\). Under the exogeneity assumption of this variable, the heterogenous parameters can be estimated from the \({\boldsymbol{y}}_{t}={\boldsymbol{\Phi }}{\boldsymbol{y}}_{t-1}+{\boldsymbol{\Lambda }}{\boldsymbol{W}}{\boldsymbol{y}}_{t-1}+{\boldsymbol{\mu }}_{0}\odot ({\boldsymbol{\iota }}_{N}-{\boldsymbol{s}}_{t})+{\boldsymbol{\mu }}_{1}\odot {\boldsymbol{s}}_{t}+{\boldsymbol{\varepsilon }}_{t}\), where \({\boldsymbol{\Lambda }}=\mathrm{diag}({\lambda }_{1},{\lambda }_{2},\dots ,{\lambda }_{N})\) is an \(N\times N\) diagonal matrix with parameter \({\lambda }_{n}\). Note that the simultaneous inclusion of the spatial lag variables \({\boldsymbol{W}}{\boldsymbol{y}}_{t}\) and \({\boldsymbol{W}}{\boldsymbol{y}}_{t-1}\) is not considered in this study because both spatial autoregressive processes are partly overlapped, as shown in the Introduction section of Debarsy et al. (2012).
For the SWM used in this study, \({\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}\) always takes a negative value, as it does in most cases. See also Anselin and Bera (1998) for a more detailed discussion. The SWM is assumed to be exogenous and time-fixed in this study. However, the SWM can be endogenous and time-varying in the panel data analysis. See Han and Lee (2016) for more details.
The priors for \(\boldsymbol{\Omega }\), \(\boldsymbol{\mu }\), \(\boldsymbol{\Phi }\), \({\boldsymbol{p}}_{11}\), \({\boldsymbol{p}}_{00}\) are conditionally conjugate.
Our sampling method is also called Metropolis within Gibbs sampling, which indicates a hybrid sampler of the MH algorithm and the Gibbs sampling. We assume that the parameters are drawn from the Gibbs sampling in steps 2–7 and from the MH algorithm in step 8. However, consistent with Chib (2001, p. 3591), we use the notation of a multiple-block MH sampling because the Gibbs sampling is a special case of the multiple-block MH sampling.
See "Appendix B" for more details. In the process of the multi-move Gibbs sampling, it is also necessary to apply the Hamilton filter. See "Appendix C" for details of the Hamilton filter.
The Federal District became Mexico City (Ciudad de México) on January 29, 2016. In this study, we use Federal District because our data cover the period before the reform.
The estimate of \(\rho\) obtained from this value was close to the average estimate of \(\rho\) obtained among \(\eta =\{2,\dots ,8\}\). In addition, we prefer the distance-based SWM to the contiguity-based one because the former can account for continuous space across regions.
The change of the base point to measure bilateral distances may affect the spatial propagation network. This study considers the state capital as a base point of the polygon. However, there are larger cities than the state capitals within some Mexican states in terms of population. Some of these larger cities are far from the capital (e.g., longer than 100 km). For example, Mexicali is the capital of the state of Baja California, but Tijuana is the largest city. Chihuahua is the capital of the state of Chihuahua, but Ciudad Juárez is the largest city. Chetumal is the capital of the state of Quintana Roo, but Cancún is the largest city. Ciudad Victoria is the capital of the state of Tamaulipas, but the Reynosa is the largest city.
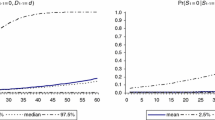
The probability of recession is calculated by \(1-{G}^{-1}{\sum }_{g=1}^{G}{s}_{t,n}^{(g)}\), where \(G\) is the number of iterations, and the superscript \((g)\) is the \(g\) th iteration. Note that our results might not identify state recessions in their entirety. Determining whether states are in recession simply depends on whether the probability of recession is higher than 0.5 or not.
Another national recession period is 2000:Aug–2003:Sep. However, we were not able to identify state recessions for that period because of data limitations.
Campeche showed a different trend from the other states. Annual growth rates of real GSP (2013 = 100) were highly negative, such as \(-1.98\)% in 2004–2005, \(-2.34\)% in 2005–2006, \(-6.58\)% in 2006–2007, \(-8.48\)% in 2007–2008, \(-9.97\)% in 2008–2009, \(-3.43\)% in 2009–2010, and \(-3.64\)% in 2010–2011. This tendency is consistent with our estimation results in Table 2.
Estimation of the Markov switching model was conducted using Ox Professional 7.20 (Doornik and Ooms 2006).
The complete estimation results are available in Supplementary Information.
The constant term is suppressed because the sum of shares equals 1. Campeche, Quintana Roo, and Tabasco are excluded as outliers because in these states, the mining and commerce, restaurant, and hotel sectors are comparatively large.
In this framework, the spillover effects are symmetric between the two regimes of economic recession and expansion. However, they could be asymmetric if the degree of spatial dependence changes between recession and expansion phases.
Holloway et al. (2002) originally set the interval to [0.4, 0.6], and LeSage and Pace (2009, Ch. 5) adopted the same strategy. We chose a slightly wider interval of the acceptance rate. The aim of tuning the proposals is to ensure that the MH sampling moves over the entire conditional distribution. Thus, we adjust the tuning parameter c in the following way. First, we set c=1 as an initial value. Next, the tuning parameter c is adjusted by scale factor 1.01 depending on the acceptance rate (c × 1.01 if the acceptance rate exceeds 0.7, while c/1.01 if the acceptance rate falls below 0.3).
References
Albert JH, Chib S (1993) Bayes inference via Gibbs sampling of autoregressive time series subject to Markov mean and variance shifts. J Bus Econ Stat 11(1):1–15. https://doi.org/10.1080/07350015.1993.10509929
Alvarado J, Quroga M, Torre L, Chiquar D (2019) Regional input-output matrices and an application to analyze a manufacturing export shock in Mexico. Ens Rev Econ 38(2):227–258
Anselin L (1988) Spatial econometrics: methods and models. Kluwer Academic Press, Dordrecht
Anselin L (2003) Spatial externalities, spatial multipliers, and spatial econometrics. Int Reg Sci Rev 26(2):153–166. https://doi.org/10.1177/0160017602250972
Anselin L, Bera AK (1998) Spatial dependence in linear regression models with an introduction to spatial econometrics. In: Ullah A, Giles DEA (eds) Handbook of Applied Economic Statistics. Marcel Dekkar, New York, pp 237–289
Aquaro M, Bailey N, Pesaran MH (2021) Estimation and inference for spatial models with heterogeneous coefficients: an application to US house prices. J Appl Econ 36(1):18–44. https://doi.org/10.1002/jae.2792
Autant-Bernard C, LeSage JP (2019) A heterogeneous coefficient approach to the knowledge production function. Spat Econ Anal 14(2):196–218. https://doi.org/10.1080/17421772.2019.1562201
Burns AF, Mitchell WC (1946) Measuring business cycles. National Bureau of Economic Research, New York
Chib S (1995) Marginal likelihood from the Gibbs output. J Amer Stat Ass 90(432):1313–1321. https://doi.org/10.1080/01621459.1995.10476635
Chib S (1996) Calculating posterior distributions and modal estimates in Markov mixture models. J Econom 75(1):79–97. https://doi.org/10.1016/0304-4076(95)01770-4
Chib S (2001) Markov chain Monte Carlo methods: computation and inference. In: Heckman JJ, Leamer EE (eds) Handbook of Econometrics, vol 5. Elsevier, Amsterdam, pp 3569–3649
Chib S, Jeliazkov I (2001) Marginal likelihood from the Metropolis-Hastings output. J Amer Stat Ass 96(453):270–281. https://doi.org/10.1198/016214501750332848
Chiquiar D, Ramos-Francia M (2005) Trade and business-cycle synchronization: evidence from Mexican and U.S. manufacturing industries. N Amer J Econ Finance 16(2):187–216. https://doi.org/10.1016/j.najef.2004.12.001
Debarsy N, Ertur C, LeSage JP (2012) Interpreting dynamic space–time panel data models. Stat Methodol 9(1–2):158–171. https://doi.org/10.1016/j.stamet.2011.02.002
Delajara M (2011) Comovimiento regional del empleo durante el ciclo económico en México. El Trimestre Económico 78(311):613–642
Doornik JA, Ooms M (2006) Introduction to Ox. Timberlake Consultants Press, London. http://www.doornik.com/. Accessed 29 May 2021
Ductor L, Leiva-Leon D (2016) Dynamics of global business cycle interdependence. J Int Econ 102:110–127. https://doi.org/10.1016/j.jinteco.2016.07.003
Elhorst JP, Gross M, Tereanu E (2021) Cross-sectional dependence and spillovers in space and time: where spatial econometrics and global VAR models meet. J Econ Surv 35(1):192–226. https://doi.org/10.1111/joes.12391
Erquizio-Espinal A (2010) Gran recesión 2008–2009 en EE.UU. y México: un enfoque regional. Paradigma Económico 2(2):5–40
Hamilton JD (1989) A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57(2):357–384. https://doi.org/10.2307/1912559
Hamilton JD, Owyang MT (2012) The propagation of regional recessions. Rev Econ Stat 94(4):935–947. https://doi.org/10.1162/REST_a_00197
Hamilton JD (2008) Regime switching models. In: Durlauf SN, Blume LE (eds) The New Palgrave Dictionary of Economics, vol. 7, 2nd edn. Palgrave Macmillan, New York, pp 53–57
Han X, Lee LF (2016) Bayesian analysis of spatial panel autoregressive models with time-varying endogenous spatial weight Matrices, common factors, and random coefficients. J Bus Econ Stat 34(4):642–660. https://doi.org/10.1080/07350015.2016.1167058
Hirata H, Kose MA, Otrok C (2013) Regionalization vs. globalization. IMF Working Papers 13/19.
Holloway G, Shankar B, Rahman S (2002) Bayesian spatial probit estimation: a primer and an application to HYV rice adoption. Agr Econ 27(3):383–402. https://doi.org/10.1016/S0169-5150(02)00070-1
Hwu ST, Kim CJ (2020) Markov-switching models with unknown error distributions: identification and inference within the Bayesian framework. Mimeo. https://indico.hias.hit-u.ac.jp/event/128/contributions/490/attachments/35/53/02_Chang-Jin_Kim.pdf Accessed 15 October 2021.
Kim CJ, Nelson CR (1998) Business cycle turning points, a new coincident index, and tests of duration dependence based on a dynamic factor model with regime switching. Rev Econ Stat 80(2):188–201. https://doi.org/10.1162/003465398557447
Kim CJ, Nelson CR (1999a) Has the U.S. economy become more stable? a Bayesian approach based on a Markov-switching model of the business cycle. Rev Econ Stat 81(4):608–616. https://doi.org/10.1162/003465399558472
Kim CJ, Nelson CR (1999b) State-space models with regime switching: classical and Gibbs-sampling approaches with applications. MIT Press, Cambridge, MA
Kose MA, Otrok C, Whiteman CH (2003) International business cycles: world, region, and country-specific factors. Amer Econ Rev 93(4):1216–1239. https://doi.org/10.1257/000282803769206278
Lee L-F, Yu J (2010) Estimation of spatial autoregressive panel data models with fixed effects. J Econom 154(2):165–185. https://doi.org/10.1016/j.jeconom.2009.08.001
LeSage JP, Pace RK (2009) Introduction to spatial econometrics. CRC Press, Boca Raton
Mejía-Reyes P, Campos-Chávez J (2011) Are the Mexican states and the United States business cycles synchronized? evidence from the manufacturing production. Economía Mexicana Nueva Época 20(1):79–112
Mejía-Reyes P, Erquizio-Espinal A (2012) Expansiones y recesiones en los Estados de México. Pearson Educación-Universidad de Sonora, Hermosillo
Mejía-Reyes P, Rendón-Rojas L, Vergara-González R, Aroca P (2018) International synchronization of the Mexican states business cycles: explaining factors. N Amer J Econ Finance 44:278–288. https://doi.org/10.1016/j.najef.2018.01.009
Ohtsuka Y (2010) Estimation of regional business cycle in Japan with Markov switching spatial autoregressive-AR model. J Jpn Stat Soc (Japanese Version) 40(2):89–109 (in Japanese)
Ord K (1975) Estimation methods for models of spatial interaction. J Amer Stat Ass 70(349):120–126. https://doi.org/10.1080/01621459.1975.10480272
Owyang MT, Piger J, Wall HJ (2005) Business cycle phases in U.S. states. Rev Econ Stat 87(4):604–616. https://doi.org/10.1162/003465305775098198
Owyang MT, Piger JM, Wall HJ, Wheeler CH (2008) The economic performance of cities: a Markov-switching approach. J Urban Econ 64(3):538–550. https://doi.org/10.1016/j.jue.2008.05.006
Owyang MT, Rapach DE, Wall HJ (2009) States and the business cycle. J Urban Econ 65(2):181–194. https://doi.org/10.1016/j.jue.2008.11.001
Sosa S (2008) External shocks and business cycle fluctuations in Mexico: how important are U.S. factors? IMF Working Papers 2008/100. https://doi.org/10.5089/9781451869613.001
Stock JH, Watson MW (1989) New indexes of coincident and leading economic indicators. In: Blanchard OJ, Fischer S (eds) NBER Macroeconomics Annual 1989, vol 4. MIT Press. Cambridge, MA, pp 351–409
Torres A, Vela O (2003) Trade integration and synchronization between the business cycles of Mexico and the United States. N Amer J Econ Finance 14(3):319–342. https://doi.org/10.1016/S1062-9408(03)00025-1
World Bank (2009) World development report 2009: reshaping economic geography. World Bank, Washington, DC
Yu J, de Jong R, Lee LF (2008) Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large. J Econom 146(1):118–134. https://doi.org/10.1016/j.jeconom.2008.08.002
Acknowledgements
I would like to specially thank Editor-in-Chief James P. LeSage, two anonymous reviewers, Alfredo Erquizio Espinal, and Kensuke Teshima for their insightful comments and helpful suggestions. I also thank Arthur Getis, Nobuaki Hamaguchi, Yoichi Matsubayashi, Akio Namba, Tatsuyoshi Okimoto, Sergio J. Rey, Andrzej Torój, Carlos Urrutia, and participants at the 2013 Spring Meeting of the Japanese Economic Association, the Rokko Forum at Kobe University, and the 53rd annual meeting of the Western Regional Science Association for their useful comments and suggestions. I acknowledge use of computer routines described in Kim and Nelson (1999b). Naturally, any remaining errors are my own. Furthermore, I am grateful for the benefits received during my stay at the Instituto Tecnológico Autónomo de México in 2012–2013. This research was carried out under a scholarship granted by the Government of Mexico, through the Ministry of Foreign Affairs of Mexico. This paper received the 2013 Kanematsu Fellowship Award from the Research Institute for Economics and Business Administration, Kobe University.
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
Not applicable.
Corresponding author
Ethics declarations
Conflicts of interest
The author declares no competing interests.
Supplementary information
Supplementary_Information.pdf.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix A Drawing \({\varvec{\rho}}\) by the metropolis–hastings algorithm
We use a truncated normal distribution as a proposal distribution. When the random variable \(x\) has the truncated normal distribution \({\mathrm{TN}}_{(a,b)}(\mu ,{\sigma }^{2})\), the probability density function (p.d.f.) is as follows:
where \(\phi (\cdot )\) and \(\Phi (\cdot )\) are the p.d.f. and the cumulative distribution function (c.d.f.) of the standard normal distribution, respectively.
To avoid high autocorrelation and poor mixing, generating \(\rho\) from the posterior distributions is repeated \(H\) times within the \(g\) th iteration. Superscript \((h)\) refers to the sample from the posterior distributions obtained in the \(h\) th iteration within the \(g\) th iteration as \({\rho }^{(g-1,h)}\). Note that the index \(h\) is reset in each \(g\) th iteration.
We use the probability integral transformation method for sampling from the truncated normal distribution. We set \({\mu }^{(g-1,h)}={\rho }^{(g-1,h)}\), \({\sigma }^{2}=1\), \(a=1/{\omega }_{\mathrm{min}}\), and \(b=1\). Following Holloway et al. (2002), we introduce a tuning parameter \(c\) into the variance term, so that the acceptance rate might fall within the interval [\(0.3, 0.7\)].Footnote 24
For convenience of explanation, we omit the superscript \((g-1)\) as \({\rho }^{(h)}={\rho }^{(g-1, h)}\). Note that \({\rho }^{(g-1)}={\rho }^{(g-\mathrm{1,0})}\) if \(h=0\). When \(u\) is distributed as a uniform distribution \(\mathrm{U}(\mathrm{0,1})\), we can draw \({\rho }^{\prime}\) from \({\mathrm{TN}}_{(1/{\omega }_{\mathrm{min}},1)}({\rho }^{(h-1)},1)\) as follows:
The acceptance probability \(\alpha ({\rho }^{(h-1)},{\rho }^{{\prime}})\) is calculated by:
where \(\pi (\rho |{\varvec{Y}},{{\varvec{S}}}^{(h)},{\boldsymbol{\Omega }}^{(h)},{{\varvec{\mu}}}^{(h)},{\boldsymbol{\Phi }}^{(h)})\) is calculated from Eq. (10). Because a standard normal distribution is symmetric, \(\phi ({\rho }^{{\prime}},{\rho }^{(h-1)})\) and \(\phi ({\rho }^{(h-1)},{\rho }^{{\prime}})\) are offset. We repeat this step \(H=10\) times in each \(g\) th iteration to avoid high autocorrelation and poor mixing. Following step 8(c) in the algorithm, we judge whether \({\rho }^{{\prime}}\) is accepted or not after the \(H\) iteration as follows:
Appendix B Multi-move Gibbs sampling for \({{\varvec{s}}}_{{\varvec{n}}}\)
Kim and Nelson (1998, 1999a, b) were the first to apply multi-move Gibbs sampling to a Markov switching model. Our explanation here is based on Kim and Nelson (1999b). For convenience of explanation, we define vectors \({\tilde{{\varvec{s}}}}_{n}^{t}\) and \({{\varvec{s}}}_{n}^{t}\), and a matrix \({\tilde{{\varvec{Y}}}}^{t}\) using the following notation:
The aim here is to obtain \(p({\tilde{{\varvec{s}}}}_{n}^{T}|{\tilde{{\varvec{Y}}}}^{T},{\varvec{\theta}})\). This can be rewritten as follows:
Furthermore, the second term can be expressed as follows:
where the first term on the RHS represents the transition probability. Incorporating the normalizing constant, we have the following probability mass function:
where \(p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t},{\varvec{\theta}})\) is calculated using the Hamilton filter (see "Appendix C" for details). The calculation step for Eq. (28) can be summarized as follows: First, we draw \({s}_{T,n}\) conditional on \({\tilde{{\varvec{Y}}}}^{T}\) and \({\varvec{\theta}}\); second, given \({s}_{T,n}\), the sampling \({s}_{t,n}\) for \(t=T-1,\dots ,1\) is implemented by backward recursion based on Eq. (30).
Appendix C Hamilton filter with spatial lag
Hamilton’s (1989) filter is applied to calculate the conditional probabilities \(p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t},{\varvec{\theta}})\) for region \(n\) at date \(t\). Based on Chib (1996, 2001), we explain how the Hamilton filter is applied in this study. Using scalar notation, model (2) can be rewritten as follows:
For the conditional p.d.f. \(f({y}_{t,n}|{s}_{t,n},{{\varvec{y}}}_{t,-n},{\varvec{\theta}})\), the expected value and variance become \(\mathrm{E}({y}_{t,n}|{s}_{t,n},{{\varvec{y}}}_{t,-n},{\varvec{\theta}}) =\rho {\sum }_{m=1}^{N}{w}_{nm}{y}_{t,m}+{\phi }_{n}{y}_{t-1,n}+{\mu }_{n,0}(1-{s}_{t,n})+{\mu }_{n,1}{s}_{t,n}\) and \(\mathrm{Var}({y}_{t,n}|{s}_{t,n},{{\varvec{y}}}_{t,-n},{\varvec{\theta}})={\sigma }_{n}^{2}\), where the subscript \(-n\) of \({{\varvec{y}}}_{t,-n}\) indicates that the \(n\) th element is excluded from the vector, and for simplicity we assumed that for each region \(n\), the spatial lag \(\sum_{m=1}^{N}{w}_{nm}{y}_{t,m}\) is exogenously given. Therefore, the conditional p.d.f., which is used in the iteration process of the Hamilton filter, is given by the following:
The algorithm of the Hamilton filter consists of two steps: prediction and update. The conditional p.d.f. \(p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t},{\varvec{\theta}})\) is obtained by forward recursion \(t=1, 2, \dots , T\).
-
1.
Prediction Step: Calculate the probability
$$p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t-1},{\varvec{\theta}})=\sum_{j=0}^{1}p({s}_{t,n}=i|{s}_{t-1,n}=j,{\varvec{\theta}})p({s}_{t-1,n}=j|{\tilde{{\varvec{Y}}}}^{t-1},{\varvec{\theta}}),$$(33)where, when \(t=1\), \(p({s}_{0,n}=i|{\tilde{{\varvec{Y}}}}^{0},{\varvec{\theta}})\) is replaced by the steady-state probabilities as follows:
$${\pi }_{n,0}=\frac{1-{p}_{n,11}}{2-{p}_{n,00}-{p}_{n,11}}\,\mathrm{and}\,{\pi }_{n,1}=\frac{1-{p}_{n,00}}{2-{p}_{n,00}-{p}_{n,11}}.$$(34) -
2.
Update Step: Calculate the probability
$$p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t},{\varvec{\theta}})=\frac{f({y}_{t,n}|{s}_{t,n}=i,{{\varvec{y}}}_{t,-n},{\varvec{\theta}})p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t-1},{\varvec{\theta}})}{{\sum }_{j=0}^{1}f({y}_{t,n}|{s}_{t,n}=j,{{\varvec{y}}}_{t,-n},{\varvec{\theta}})p({s}_{t,n}=j|{\tilde{{\varvec{Y}}}}^{t-1},{\varvec{\theta}})}.$$(35)
The probabilities \(p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t},{\varvec{\theta}})\) are used in the multi-move Gibbs sampling. The probabilities \(p({s}_{t,n}=i|{\tilde{{\varvec{Y}}}}^{t-1},{\varvec{\theta}})\) are also used for calculating the likelihood function in the model selection.
Appendix D Robustness check by spatial econometrics
4.1 D. 1. Spatial autocorrelation
To investigate the time-varying spatial dependence in regional business cycles, this study calculates Moran’s \(I\) statistics across states at time \(t\) as follows:
where the SWM is based on Eq. (19), the economic and route distance between states with the distance decay parameter \(\eta =4\).
Figure 6 shows the calculation results of Moran’s \(I\) in the study period. Panel (a) shows the results in each quarterly period. The red marker indicates statistical significance at the 10% level. Importantly, spatial autocorrelation is not always significant throughout the entire period. However, spatial autocorrelation occurred during the Great Recession of 2008–2009. To mitigate the fluctuations, the centered moving average of order 3 is calculated in panel (b). The degree of spatial autocorrelation increased gradually during the Great Recession of 2008–2009 and fell after the Great Recession.
Time-series of Moran's \(I\). The variable used for Moran's \(I\) is the quarterly growth rate of the Quarterly Indicator of State Economic Activity (Indicador Trimestral de la Actividad Económica Estatal, ITAEE). The red marker indicates statistical significance at the 10% level. The spatial weight matrix is based on the gross regional products and the route distance across states with the distance decay parameter \(\eta = 4\). Centered moving average of order 3 is calculated in panel (b)
Figure 7 shows Moran’s scatterplot using annually aggregated data for 2008 and 2009. In other words, the quarterly data are pooled on a yearly basis. As discussed above, the positive spatial autocorrelation is confirmed visually during the Great Recession. Although spatial autocorrelation across regional business cycles is not obvious from the data, it is confirmed as being significant during the Great Recession.
4.2 D. 2. Spatial panel econometrics
The spatial autoregressive process of dependent variable \({\varvec{W}}{{\varvec{y}}}_{t}\) considers contemporaneous interdependence across regions. One may consider another possibility of a spatial autoregressive process, that is, \({\varvec{W}}{{\varvec{y}}}_{t-1}\) instead of \({\varvec{W}}{{\varvec{y}}}_{t}\). Consider a simpler version of model (2) without a temporal autoregressive process as follows:
where \({\varvec{\mu}}=({\mu }_{1},{\mu }_{2},\dots ,{\mu }_{N})\) is the fixed effect of state \(n\). By successive iteration, we can show that \({{\varvec{y}}}_{t}=({\varvec{I}}-\rho {\varvec{W}}{)}^{-1}{\varvec{\mu}}+({\varvec{I}}-\rho {\varvec{W}}{)}^{-1}{{\varvec{\varepsilon}}}_{t}\), which is equivalent to \({{\varvec{y}}}_{t}=\rho {\varvec{W}}{{\varvec{y}}}_{t}+{\varvec{\mu}}+{{\varvec{\varepsilon}}}_{t}\). Therefore, note that simultaneous spatial autoregressive processes result from dynamic spatial dependence. See LeSage and Pace (2009) for a discussion on time dependence in spatial econometric models.
To control for common external shocks across the Mexican states, this study estimated a spatial panel econometric model with fixed effects (Lee and Yu, 2010):
where \({\varvec{\mu}}=({\mu }_{1},{\mu }_{2},\dots ,{\mu }_{N}{)}^{\top }\) is the fixed effect of state \(n\), \({\psi }_{t}\) is the fixed effect of time \(t\), and SWM is based on Eq. (19), the economic and route distance across states with the distance decay parameter \(\eta =4\). Time fixed effects aim to control for common external shocks across the county. Year and quarter and year \(\times\) quarter fixed effects are included. The parameter of interest is \(\rho\), which measures the spatial dependence in economic activities.
Table 7 shows the estimation results obtained by maximum likelihood estimation. In column (1), in which time fixed effects are not controlled for, the estimate of \(\rho\) is 0.230 and significantly positive throughout the entire period. When the year and quarter fixed effects are controlled for in column (2), the magnitude of spatial dependence becomes 0.199 but remains statistically significant at the 1% level. When the year \(\times\) quarter fixed effects are controlled for in column (3), the magnitude of spatial dependence becomes 0.028 and is statistically insignificant.
To estimate spatial dependence in regional business cycles under control for common external shocks, the entire period is divided into three subperiods. In columns (4) and (6), the coefficient estimates of the spatial lag are insignificant and close to zero in the pre and post periods of the Great Recession. In column (5), the parameter estimate of spatial dependence is 0.236 and significantly positive at the 10% level only during the Great Recession of 2008:Q2–2009:Q2, suggesting that significant spatial dependence in a subperiod results in statistical significance in the entire period. Note that the split of the study period is exogenously determined within this regression, although the Markov switching model endogenously estimates expansion and recession phases by state.
Summing up, after controlling for common external shocks across the Mexican states, we confirmed significant spatial dependence in regional business cycles only during the Great Recession. Although time-invariant spatial dependence in regional business cycles was assumed in the model, time-varying spatial dependence in regional business cycles will be more precise. Therefore, the quantitative magnitude of spatial spillover effects on neighboring economies might have a wider range than that estimated, whereas the qualitative discussion about the spatial spillover effects does not change.
Appendix E Model selection
We use the log marginal likelihood to compare different econometric models. Chib (1995) proposed a procedure for calculating marginal likelihood under Gibbs sampling. However, in this study, a parameter measuring spatial dependence \(\rho\) is drawn by the MH algorithm, and thus we employ a method proposed by Chib and Jeliazkov (2001).
The calculation of the marginal likelihood is based on the following equation:
which is termed the basic marginal likelihood identity (BMI). The BMI consists of the likelihood function, prior distribution, and posterior distribution. This identity holds at any \({\varvec{\theta}}\). In this study, the mean of the posterior distribution \({{\varvec{\theta}}}^{*}\) is used. Thus, by taking the logarithms of the BMI and evaluating them at \({{\varvec{\theta}}}^{*}\), we can calculate the log marginal likelihood estimate as follows:
Based on Eq. (40), we calculate the following three terms: the likelihood function, the prior distribution, and the posterior distribution, all evaluated at \({{\varvec{\theta}}}^{*}\).
The first term on the RHS of Eq. (40) is the log likelihood function. Note that the Markov switching model includes hidden variables \(\{{{\varvec{s}}}_{t}{\}}_{t=1}^{T}\). The likelihood function thus takes the following form:
The second term in the brackets must be calculated in advance. This term can be obtained from the prediction step in the Hamilton filter.
The second term on the RHS of Eq. (40) is the logarithm of the joint prior distribution. As we assumed an independent prior distribution across parameters and regions, the prior distribution can be obtained as follows:
The third term on the RHS of Eq. (40) is the logarithm of the joint posterior distribution, which can be rewritten as follows:
where
The superscript \((g)\) refers to the sample from the posterior distribution in the \(g\) th iteration and \((k)\) refers to the sample from the reduced Gibbs runs obtained in the \(k\) th iteration. Note that some of the parameters are given as a mean in the reduced Gibbs runs, and that \({\rho }^{(k)}\) is drawn from a proposal distribution \(q({\rho }^{*},{\rho }^{(k)})\). Besides the \(G\) iterations, we need to implement an additional \(5\times J\) iterations for the reduced Gibbs runs. The first reduced run is for the denominator of \(\widehat{\pi }({\rho }^{*}|{\varvec{Y}})\) and \(\widehat{\pi }({\sigma }_{n}^{2*}|{\rho }^{*},{\varvec{Y}})\); the second is for \(\widehat{\pi }\left({{\varvec{\mu}}}_{n}^{*}|{\rho }^{*},{\sigma }_{n}^{2*},{\varvec{Y}}\right);\) the third is for \(\widehat{\pi }\left({\phi }_{n}^{*}|{\rho }^{*},{\sigma }_{n}^{2*},{{\varvec{\mu}}}_{n}^{*},{\varvec{Y}}\right);\) the fourth is for \(\widehat{\pi }({p}_{n,11}^{*}|{\rho }^{*},{\sigma }_{n}^{2*},{{\varvec{\mu}}}_{n}^{*},{\phi }_{n}^{*},{\varvec{Y}})\); and the fifth is for \(\widehat{\pi }({p}_{n,00}^{*}|{\rho }^{*},{\sigma }_{n}^{2*},{{\varvec{\mu}}}_{n}^{*},{\phi }_{n}^{*},{p}_{n,11}^{*},{\varvec{Y}})\). We set \(J\) to have the same number of iterations as \(G\). Moreover, the numerical standard errors of the marginal likelihood estimates are also calculated. For calculation of the numerical standard errors, we need to select a lag at which the autocorrelation is small enough to be neglected. Thus, we set the lag length equal to 40. See Chib and Jeliazkov (2001) for more details.
Table 8 presents the log marginal likelihood estimates with numerical standard errors using the different econometric models. First, it is useful to compare estimates of the log marginal likelihood between the Markov switching model with a spatial autoregressive process (MS-SAR) and the Markov switching (MS) model because MS is a spatial case of MS-SAR when \(\rho =0\). Consequently, it is supported to take into account spatial dependence in regional business cycles. Our estimation results also indicate that the Markov switching model with a first-order autoregressive process MS-AR(1) fits the data almost as well as MS-SAR. The Markov switching model with a spatial autoregressive process and a first-order autoregressive process MS-SAR-AR(1) is supported against MS-AR(1) or MS-SAR. See Supplementary Information for the full estimation results of MS, MS-AR(1), MS-SAR, and MS-SAR-AR(1).
Appendix F Map of Mexico
State codes and names appear in Fig. 8. In the empirical analysis, the 32 states are divided into two groups in terms of the manufacturing specialization index. Average specialization index of manufacturing sector between 2003 and 2005 is used. Colored states show the manufacturing specialization index above the median. Figure 9 shows details of the geographical distribution of manufacturing specialization index.
Rights and permissions
About this article
Cite this article
Kondo, K. Spatial dependence in regional business cycles: evidence from Mexican states. J Spat Econometrics 3, 1 (2022). https://doi.org/10.1007/s43071-021-00018-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43071-021-00018-z
Keywords
- Spatial dependence
- Spatial spillover effects
- Regional business cycles
- Markov switching model
- Markov chain Monte Carlo