1 Introduction

Research on optimization of real-time bidding is mainly focused on the problem of bidding for display advertising [1, 2], which has been made relevant by the need to optimize a Google Ads account, typically with the aim to maximize incoming click traffic to the advertiser’s landing page. However, the range of applications of such real-time support is much wider, and the peculiarities of a specific application reflect on the elements of the algorithms that best support it.

This work describes an end-to-end application supporting real-time bidding for team selection in fantasy football. The application includes data acquisition, feature engineering, mathematical modeling, prediction analytics, adaptive prescriptive optimization, a distributed, front-end implementation of the support module, and league simulations for computational validation.

While none of the techniques used in the application expands the state of the art of the respective area, we believe that their combination into a full-stack, easily accessible pipeline expands the level of support that is currently achievable by predictive and prescriptive analytics in newly encountered scenarios.

The application area addressed in this work is support for bidding in auction drafts for fantasy football team selection. This is an auction where a number of participants bid in rounds for one team player at a time until all teams have their roster complete. Each participant has a fixed overall budget and tries to maximize the expected performance of his/her team in the season to follow.

Two issues emerge as preeminent: the ability to assess the expected performance of each available athlete and the ability to allocate scarce resources to different options in order to get the best possible combination in a competitive environment. Bidding decisions must be made in real time and in a dynamically changing situation, where alternatives can disappear because other participants acquire a player of interest, and where acquisition prices vary because other participants have raised their offer for the currently auctioned player.

These two concerns can be addressed by predictive and by prescriptive analytics algorithms, respectively, under different constraints on real-time usage. This work reports about a system that incorporates all necessary modules of a computer-based assisted support for an auction participant.

Validation of the effectiveness of the proposed teams is made via a further module that simulates fantasy football leagues using actual, out-of-sample match results. Teams recruited using different budget availabilities are used as a basis for defining the day to day lineups for each match, compatible with the formations allowed by the fantasy football regulations. Leagues including teams made by the most expensive players show the effectiveness of the approach.

2 Fantasy Football

Fantasy sports, which fantasy football is an instance of, have more than 60 years of history and offer fans an opportunity to create an own version of their sport of liking [3]. A fantasy sport participant act as owner and manager of her/his own team, typically first bidding for the players to enter the team (draft phase) and then deciding for each match which one of the acquired players will be used in the match (lineup phase).

A team does not need to be composed of players who actually play together in real-world events, and its effectiveness is computed after the actual performance of the players in real-world sport events. There exist agencies that compute for each player and for each event a score in “fantasy points”, and the success level of a fantasy team on a match day is given by the sum of the fantasy points gained by the used players in the actual real-world corresponding matches.

The players that actually play a match are a subset of those in the drafted team. Each match can be played by a different subset of the team’s players, but the subset usually cannot be freely chosen. In the case of fantasy football, for example, feasible subsets must comply with acceptable formations. Formations are described by categorizing the players except for the goalkeeper according to their positioning along (not across) the pitch. The more defensive players are given first, then midfielders, then possibly attacking midfielders, and finally forwards. For example, 4-4-2 means four defenders, four midfielders, and two forwards. Currently, in Italian fantasy football, the full set of feasible formations is: 3-4-3, 3-4-1-2, 3-4-2-1, 3-5-2, 3-5-1-1, 4-3-3, 4-3-1-2, 4-4-2, 4-1-4-1, 4-4-1-1, 4-2-3-1.

The objective of a fantasy team manager in the draft phase is thus to select a set of players that is expected to earn as many fantasy points as possible during the future season. Each manager lists his fantasy team into a contest (a league), where the team is ranked among all other fantasy teams that entered the same contest. Contests can be freely organized by groups of friends, but many managers choose to pay an entry fee in the hope of winning contest prizes. Fantasy sports therefore generate an economically relevant industry, moving billions of dollars worldwide [4]. Entry fees for structured contests range from free to over $10,000 per entry, and some contests pay out prizes of up to one million dollars. Participants also invest money into decision-making support tools, leading to an estimate of multi-million annual spending to purchase additional information and decision-making tools [5].

Given the figures, it is unsurprising that algorithms have been studied to support related decisions, even though the use of mathematical programming for fantasy sports is still limited. Most research was targeted to American football (NFL) fantasy draft, possibly also due to the higher monetary prizes compared to Fantasy Football leagues. This is especially true for non-academic contributions (f.e., [6,7,8]). However, there are differences in the sports that make intrinsically different the problems faced for the American or for the otherwise worldwide accepted football. Surely, articles related to Fantasy Football exist and make use of different approaches for maximizing the expected points of the fantasy team subject to budget restrictions. An early attempt used Bayesian reinforcement learning [9] for sequential team formation in Fantasy Premier League, modeling decisions as a belief-state Markov Decision Problem and solving it using Bayesian Q-learning. Stochastic integer programming was proposed in [10] taking into account the possibility that the chosen players will earn a distribution of fantasy points, rather than a single predetermined value. A recent survey on scheduling in sports analytics with special reference to Latin America is presented in [11].

Closer to the approach proposed in this work, Bonomo et al. [12] presented two optimization models for the Argentinian Fantasy Football. The first model, called a priori, determines lineups and transfers based on predictions of player points, while the second model, called a posteriori, determines which would have been the optimal lineups when data were known beforehand. In addition to the optimization model, they also forecast future player points for the individual players by a very basic strategy: the forecasts were calculated by averaging the points obtained in the three last gameweeks for each particular player. A similar approach is described in [13], and a related one applied to cycling is described in [14].

The task of predicting players’ performance is a core element of team drafting and has generated a whole literature of its own. Predictions range from individual players to whole teams, these last were first tackled for the NFL [15] and eventually moved to other leagues as well [16, 17]. However, working on the forecast of athlete performance does not fall within the scope of this paper, which is on online bidding support. For our purpose, we will content ourselves with state-of-the-art, univariate forecast techniques.

A further related topic is the determination of players’ market values, which have traditionally been estimated by football experts, but crowdsourcing has recently emerged as an alternative approach. High correlations have been found between actual transfer fees and crowdsourced market values, but unfortunately obtaining these last suffers from severe practical limitations. However, data-driven estimates of market value can overcome several of the crowd’s practical limitations while producing comparably accurate numbers [18].

In the following we detail how we approached the task of online team draft optimization applied to the Italian major football league, “serie A” and how we validated the optimized suggestions by defining suitable leagues.

3 Prescriptive Analytics

The draft problem for Italian fantasy football requires, not much differently from other fantasy football leagues, to recruit 23 players with specific roles: 3 goalkeepers, 7 defenders, 8 midfielders, and 5 forwards [19]. Moreover, midfielders are further classified as pure midfielders or attacking midfielders. The lineup at each match will consist of 11 players chosen among these 23, and according to the allowed formations.

A fundamental issue is that in the draft phase, to acquire players, the manager enters an auction with the other managers of his league, where player names will be called and bids will be placed on the currently auctioned player. Each manager has a maximum budget B, usually 260 F.M. (FantaMillions), but also 300 or 500 could be allowed, or any amount agreed upon in case of leagues among friends. There is no incentive in keeping some budget after the auction, but the total offers of a manager cannot exceed the allowed budget.

Let I be the index set of all auctioned players, an IP formulation of this problem is as follows.

$$\begin{aligned} ({ P}) \qquad z_ P = max \sum _{i\in I}p_ix_i \end{aligned}$$
(1)
$$\begin{aligned} s.t. \sum _{i \in \mathcal {G}}x_i = 3 \end{aligned}$$
(2)
$$\begin{aligned} \sum _{i \in \mathcal {D}}x_i = 7 \end{aligned}$$
(3)
$$\begin{aligned} \sum _{i \in \mathcal {M}}x_i = 8 \end{aligned}$$
(4)
$$\begin{aligned} \sum _{i \in \mathcal {P}}x_i \ge 3 \end{aligned}$$
(5)
$$\begin{aligned} \sum _{i \in \mathcal {T}}x_i \ge 1 \end{aligned}$$
(6)
$$\begin{aligned} \sum _{i \in \mathcal {F}}x_i = 5 \end{aligned}$$
(7)
$$\begin{aligned} \sum _{i \in I} c_ix_i \le B \end{aligned}$$
(8)
$$\begin{aligned} x_i \in \{0,1\}, i \in I \end{aligned}$$
(9)

A binary decision variable \(x_i\) is associated with each player \(i \in I\). The objective function (1) maximizes the sum of the expected payoffs \(p_i\) of the acquired players, subject to constraints that enforce the number of goalkeepers to choose within the index set \(\mathcal {G}\) of all goalkeepers, \(\mathcal {G} \subset I\) (2), the number of defenders to choose within \(\mathcal {D} \subset I\) (3), the number of midfielders to chose within \(\mathcal {M} \subset I\) (4), with a minimum amount of pure midfielders (5) and of attacking midfielders (6), and the number of forwards to choose within \(\mathcal {F} \subset I\) (7), where (\(\mathcal {M} = \mathcal {P} \cup \mathcal {T}\) and \(I = \mathcal {G} \cup \mathcal {D} \cup \mathcal {M} \cup \mathcal {F}\)). Constraint (8) imposes the budgetary restriction and constraints 9 are the integrality constraints.

The complexity of the problem is due to the budgetary and total number of restrictions, along with the positioning of the attacking midfielders. After associating a Lagrangian penalty \(\lambda\) with the budget constraint, and relaxing the constraint, we have the formulation LGP of the Lagrangian problem:

$$\begin{aligned} ({ LGP}) \, z_{LGP} = max \sum _{i\in I}(P_i - \lambda c_i)x_i + \lambda B \end{aligned}$$
(10)
$$\begin{aligned} \begin{aligned} s.t.&(2) \ldots (7), (9) \\&\lambda \ge 0 \end{aligned} \end{aligned}$$
(11)

In this way, we have removed the only one linking constraint and the problem can be decomposed into four subproblems, defined on \(\mathcal {G}\), \(\mathcal {D}\), \(\mathcal {M}\), and \(\mathcal {F}\), respectively, that can all be solved by inspection. Moreover, having relaxed only one inequality constraint, the optimization of the Lagrangian dual is expected to be quite fast and effective.

The reason for the interest in the Lagrangian reformulation of the problem, which could clearly be otherwise easily solved by state-of-the-art MIP solvers, lies in the stated objective of supporting real-time auction bidders. Given the area of interest, it is in fact possible to imagine that bidders will be young people using a smartphone as the supporting computational device. Currently, smartphones and mobile devices in general can leverage enough computational power to support advanced optimization, but the effectiveness of mobile MIP solvers is still far from that of the desktop ones [20]. On the contrary, in our case Lagrangian optimization is much less computationally demanding and can be made easily available implementing a Lagrangian heuristic [21], even using web popular languages such as javascript. Since we expect no reduction in effectiveness when using Lagrangian algorithms, we deem this the preferable way to achieve the overall objective.

Specifically, we used a straightforward implementation of the Lagrangian heuristic detailed in [22] and [23], whose pseudocode is shown in Algorithm 1. Penalty updates are made by a standard subgradient algorithm while subproblem LR(\(\lambda\)) corresponds to formulation LGP and is immediately solved by inspection simply ordering the variables by non-increasing costs.

figure a

A further note derives from the dynamic real-time setting where the code is expected to be used. As the auction proceeds, instance data get updated, players become no options and costs increase. It is necessary to re-establish the team balance, and optimized Lagrangian penalties guarantee a warm start that usually permits to adapt the suggestion in very few heuristic iterations.

4 Predictive Analytics

The optimization model P makes use of expected payoffs \(p_i\) for each \(i \in I\). It is necessary to estimate the return on the investment on a player over the decision horizon defined by the auction. This amounts to predict results in sports, a very challenging topic that has generated a whole literature of its own [24]. Most notably, the overall setting is a typical investment setting, where auctioned assets do not guarantee stable performance, but they are subject to a variability that can compromise the value of the investment. As in any such circumstance, the investor, the bidder in our case, has two objective functions to pursue, the maximization of the expected return and the minimization of the investment risk. Purchasing a player can thus be seen as an investment, having the double objective of maximizing profit and minimizing risk.

Financial literature is rich with contributions on how to combine the two objectives into a single one. One among the simplest possibilities is the use of Sharpe’s ratio [25, 26], which is defined as the difference between the returns of the investment and the risk-free return, divided by the standard deviation of the investment. This last is taken as a measure of its volatility. The ratio quantifies therefore the marginal amount of profit that the investor receives when increasing by one the accepted risk.

The Sharpe’s ratio, that when structured as in our case is also named Information Ratio (IR), gets computed as:

$$\begin{aligned} IR = (Return - Benchmark Return) / Tracking Error \end{aligned}$$

where IR is the information ratio, Portfolio Return is the expected return of the investments for the period of interest, Benchmark Return is the expected return computed for the benchmark index, and Tracking Error in our case is the average of the negative deviations from the means, i.e., we for each player we consider only the negative deviations from his means and we compute their standard deviation.

Actually, given that in our case we do not have a risk-free option, we compare the expected return of each asset with a benchmark, computed as the minimum forecast profit among players with the same role. Volatility was measured as the average negative deviation, as mentioned.

Obtaining the expected return corresponds to predicting fantasy points, a task that is complicated by the nature of the relevant data series, which are typically very incomplete, with high variance and containing a relatively low number of sample points. Moreover, data is clearly affected by externals (the team a player plays for, his fitness condition on the day of a match, manager and team pressures, etc.), which are often hard or impossible to include.

Player evaluation, therefore, goes through a pipeline consisting of

  1. 1.

    data filling,

  2. 2.

    data series forecast,

  3. 3.

    IR quantification.

The overall objective is the selection, within the available budget, of a team that proves effective in the time horizon when no more players can be acquired, in our case in the next 19 matches (serie A league is played by 20 teams).

We developed a full-stack forecast module, downloading data from available sources, preprocessing them, fitting in-sample models and using them for out-of-sample forecasts. Each phase was implemented in different, alternative ways, in order to get the best possible pipeline. The quality of each alternative could be ascertained only by the performance of the team ultimately selected on data based also on that alternative.

Data acquisition and data cleaning were relatively straightforward. We downloaded the data series of all players for the seasons starting from 2014 - 2015 up to the last match of the first half of season 2020–2021 [27], amounting to 266 matches. We then did some data cleaning to ensure the significance of the analyzed data, and we removed all series of players who:

  1. 1.

    played less than 50% of the matches in the interval between the first and the last match they could have been available to their team;

  2. 2.

    did not have contiguous runs longer than 10 matches they did not play, though available;

  3. 3.

    played at least 45 matches overall.

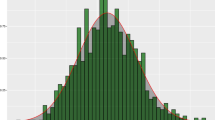
Figure 1 shows the distribution of the number of played matches for the whole set of players. The average number of played matches for the selected players was 101.88 over 266, while it was 45.88 for the whole set of 1623 players.

The successive filterings of the downloaded data led to the following figures:

  • 1623 players downloaded,

  • 621 played in season 2020–21,

  • 586 played in the first half of the 2020–21 season (necessary, not sufficient, for forecasting),

  • 511 of these played also in the second half-season (can be bought),

  • 481 of these played at least two seasons (min series length),

  • 161 of these satisfied the three requirements above (min data for forecasting).

Fig. 1
figure 1

Distribution of number of matches per player

Full size image

So-called data wrangling involved mainly filling missing data, as no player played all matches and we needed complete series for reliable forecasting, at least, as reliable as we could get. We tried different methods, including linear interpolation, rolling average, knn mean, and other python-based methods, but the overall best performance (though without statistical significance, just considering the effectiveness of the resulting teams in the final leagues) was obtained by using a support vector regressor (SVR, see Fig. 2, where the effects of some different approaches are shown, and Fig. 3, where the regression line is plotted against actual points). SVR has shown both the advantage of not dragging onto missing data the possible outliers (not to be removed) present just before or after the gap, and of providing a regression model which is synchronized with ground data, while moving averages tend to shift forward outliers, thus limiting their significance when used as baselines for forecast models. Note that SVR can also be used for forecasting, and will in fact be one of the options tested when comparing drafted teams.

Fig. 2
figure 2

Different filling strategies. a Backfill. b Forward fill. c Mean fill. d SVR fill

Full size image

Further analysis has shown that there rarely is a significant seasonality in the series and that the actual vote series, as provided by specialized agencies, can usually be loosely modeled as normally distributed, but this is not the case for the distribution of fantasy points.

We finally moved to forecast future player performance, as measured by fantasy points. The horizon of interest for this forecast was half a season, as this is the period of time during which players can not be exchanged in the fantasy league of interest to us. To learn the models, we partitioned, for each player, the data series into a train set consisting of all initial data but the last 19 available matches and a test set containing the remaining points, upon which the loss function is quantified.

Fig. 3
figure 3

SVR regression

Full size image

The draft problem would be sufficiently solved by forecasting the average value of the test set, which corresponds to the \(p_i\) of the corresponding player, using the notation of formulation (P) presented in Sect. 3. As we plan to cover also the lineup problem, we tried however to get as detailed as possible forecasts.

4.1 Forecast

It is notoriously implausible to reliably forecast detailed sports results, however, averaged values and trends are more amenable to forecast. We set out to forecast sequences of 19 match points using the filled time series obtained as described in Sect. 4. To mitigate randomness, we worked on series produced by the SVR regressor. We tested different forecasting methods: MLP (from TensorFlow, [28]), SVR (from scikit-learn, [29]), LSTM ([30], again from tensorflow), SARIMA (SAR, [31], from pmdarima [32]), Random Forests (RF, [33], from scikit-learn), and decision trees (DT, from scikit-learn). Hyperparameters for each of them were set after a grid search, that we implemented ourselves except for SARIMA, which has a python auto-arima function available.

Figure 4 shows an example of the analysis of significance of the forecast result. For each method and for each player we computed the RMSE on the testset, in order to determine whether different methods provided significantly different accuracies. First, a normality test determined that none of the methods generated RMSE results that were normally distributed over the set of players. We, therefore, applied a nonparametric, Mann-Whitney U test to each pair of methods in order to determine the significance of their produced results. Figure 4a contains a heatmap of the test results and Fig. 4b one for the difference of means of results obtained by the tested algorithms.

As apparent from Fig. 4b, the only approach that caused significantly different means was MLP, and that was because in two cases its forecasts diverged, causing the shown results. When these two outliers are not considered, MLP results become aligned with those of the other algorithms. Analyzing the significance of the pairwise comparisons, it appears that LSTM and SARIMA are more reliable than the remaining approaches, but the sheer amount of the RMSE errors does not suggest putting much greater faith on these two methods than on the other four ones.

Fig. 4
figure 4

Significance of means differences. a Mann-Whitney U probabilities. b Differences of means

Full size image

Figure 5 shows, for four players, the performance in the first half-season (fantasy points, together with its 4-day moving average and its SVR regression), and the forecasts proposed by the six approaches for the second half-season, superimposed to the actual data as available at the end of the season. Figure 5a reports the case with the best RMSE, but that is only because the player was rarely utilized in the last matches and, as it turned out, with average results. The other subfigures show heavily utilized players, and in these cases a high variance is apparent. Nevertheless, while some methods (DT, RF) can do no better than predict a constant value, other ones propose more varied forecasts. This possibility will be exploited in the following lineup phase.

As a side note, we point out that different hyperparameter settings could obviously give rise to different behaviors, but the objective of this part of the work is not to find the most effective forecast approach, rather, to exploit the state of the art allowing reasonable computational resources and building on the obtained results.

Fig. 5
figure 5

Single player forecasts. a Bourabia forecast. b de Ligt forecast. c Lukaku forecast. d Ronaldo forecast

Full size image

4.2 Lineup

The draft phase terminates defining the 23 players each manager can use when taking part to a league, but for each match, 11 out of the 23 players must be selected. This gives rise to a lineup problem to be solved prior to each match. The only constraint to the lineup solution is that the selected players must conform to one of the allowed formations (3-4-3, 3-4-1-2, \(\ldots\) , 4-2-3-1).

The lineup problem requires therefore first to determine which formation is to be used in the next match, then which players will be selected for the different roles. However, having just 23 players to choose from, the search space is quite limited and the lineup problem can be efficiently solved by exhaustive search. Lineups can in fact be defined first by selecting for each formation the subsets of players with the highest expected profits in the role, then selecting the formation that maximizes the total expected profit.

A relevant point, in this case, is that the decision for each match can be made knowing the complete fantasy points time series up to the last match, and forecasts need to be made only for one value ahead. This permits a much more reliable forecast, upon which to define the lineup. Again, this forecast can be made using any of the algorithms used in Sect. 4.1, we used for each player the same algorithm that was used for drafting the team (i.e., if the team was drafted using DT, we also solved the lineup based on DT one point ahead forecasts). Figure 6 presents three such forecasts based on LSTM. For each player the complete blue line is the SVR regression, the left red line is for in-sample validation while the right green line is for out-of-sample results. It can be seen how these forecasts rapidly adapt to performance changes, thus supporting different lineups for different matches.

Fig. 6
figure 6

One point ahead forecasts

Full size image

5 Deployment

The deployment of the above described methods has been made on two different platforms: a python-based server that preliminarily computes all forecasts and a progressive web app written in javascript [34] for online, real-time support of auction bidding.

The server-side backend was used first to download all past fantasy point time series, then the hyperparameters of each forecast model were optimized by exhaustive grid search. Search was initialized by providing four alternative values for each hyperparameter, then enlarging the set in case a maximum or minimum value was chosen. Data download requires only a few seconds, while hyperparameter optimization was run for several days on a dedicated intel i7 server, 64 Gb of RAM. The cost function was the total MAPE resulting from each setting, computed on a fixed subset of 16 randomly chosen players. The final forecasts were produced applying the algorithms with optimized parameters to all players.

The client side front-end is more of interest. Forecast results were persisted and made available to optimization clients, which implement the bidding support. Each client runs its own optimization code, that consists of the Lagrangian heuristic based on subgradient optimization of the Lagrangian dual of problem LGP [21] (see Sect. 3). The code is written in javascript and can be run on any mobile platform running browsers that support Service Workers, it can be accessed from the url in [34]. The structure of the problem, with just one constraint to relax, guarantees the optimization to be fast and effective, we never had the need to stop because of reached time limits nor to include a fixing heuristic in the code because the subgradient finished with an infeasible solution.

For drafting, Sharpe’s indices were used as the values \(p_i\), \(i \in I\), present both in formulation P and in the corresponding relaxation LGP.

Before the auction begins, on each client a first optimization determines a target ideal team, as a function of the available budget. As the auction proceeds, problem data can be updated and the optimizer restarted over the new values, thus adapting the incumbent Lagrangian multipliers and heuristic solution. All optimizations and reoptimizations run at most in a couple of seconds CPU time on a contemporary smartphone.

Lineup optimization could have been made available for mobiles as well, but since this falls outside of the scope of this research, we just implemented it (in c#) and ran it on a desktop. Optimization times were negligible. Lineups are of relevance for league simulations, as described in the following Sect. 6.

6 Computational Experience

The objective of this work is that of devising an algorithmic solution that can support a bidder in drafting a football team, that will ultimately prove effective in fantasy football leagues. The success of the whole method is, therefore, to be measured by the effectiveness of the drafted team when included in a league. We therefore defined a number of test leagues, each of which included different teams proposed by our algorithms as detailed in the following. The result of each match was computed using actual fantasy points from newspapers as soon as they become available for the day corresponding to that of the match (test league days are aligned to actual serie A league days).

We computed a team for each forecast algorithm and for 4 budget levels, and we benchmarked the teams against one composed by the maximum cost players for each role, as of end of Jan 2021 (not all of them available for drafting, having been in Italy for too short), and against teams optimized projecting past profits (no Sharpe’s index).

Having these teams, we simulated three different leagues:

  • Comparison among forecast algorithms and different budget levels.

  • Comparison with and without Sharpe’s index.

  • Comparison against the most expensive team.

The reported results are averages over 20 repetitions of the same half-season, played by the same teams, but scrambling the days for the matches, as results can vary much with the day of the match. Player costs in all cases were based on “official” fantasy football quotations as available at the beginning of the second half of the Serie A season from [35].

Table 1 contains results of a league meant to compare the effectiveness of teams drafted using the different forecast algorithms mentioned in Sect. 4.1 when increasing budget levels B were allowed in inequality 8. The least allowed budget is \(B=154\) because this was the least budget that allowed to complete a draft solution of 23 players that met all constraints of formulation P. We used three further increasing budget levels (200, 300, and 400) that progressively relax restrictions on draftable players, thereby simulating reduced availabilities as possibly resulting from ongoing auctions.

The columns contain the teams’ name, where the number is the budget and it is followed by the identifier of the forecasting algorithm used to draft the team, the points the team got in the league, averaged over the 20 repetitions, and the final rank of the team, again averaged over the 20 repetitions.

Table 1 Comparison of algorithms and budget levels
Full size table

An analysis of the box plots reported in Fig. 7, where data was grouped by budget, and of Fig. 8, where data was grouped by algorithm, suggests that the budget amount has a noticeable effect on the team effectiveness, while the differences due to the forecasting algorithm are not apparent. This intuition is further supported by a Kruskal-Wallis test, which — despite the scarcity of data — certifies the differences due to budget (pvalue=0.001) and accepts the null hypothesis for the difference of algorithms.

Fig. 7
figure 7

Impact of budget. a Box plot points. b Box plot ranks

Full size image

Teams are reported in Table 1 by decreasing points. Clearly, an higher available budget guarantees better performance, though no significant difference is observed between a budget of 154 and a budget of 200.

Fig. 8
figure 8

Impact of algorithm. a Box plot points. b Box plot ranks

Full size image

A second analysis was about the importance of forecasting and Sharpe’s index pricing. To this end, we defined a league where the best performing selection strategies were used based on Sharpe’s index or just on average forecasts. As the league could contain at most 20 teams (remember we drew fantasy points from Serie A actual fixtures), we kept only the higher budgets and we discarded DT as a forecasting algorithm as the least capable of getting an excellent performance.

Table 2 Comparison with and without Sharpe’s index
Full size table

Table 2 displays the results, and Fig. 9 the corresponding box plots. Here, differences are more nuanced than in the previous table, and the Kruskal-Willis test cannot reject the null hypothesis. However, it can be appreciated that best, worst, and median data for the Sharpe’s case are all better than the corresponding ones just based on forecasts.

Fig. 9
figure 9

Impact of Sharpe’s index. a Box plot points. b Box plot ranks

Full size image

Finally, we compared the best team we could get with each of the forecasting algorithms, budget 400, with a team that was composed of the 23 highest quotation players as of the beginning of the second half of the season, compatible with role constraints. After testing all formations, we selected the one that maximized the team global quotation (the “expensiveTeam”), that resulted to be 525Footnote 1. Notice that this team is suggested for all fixtures and could not be suggested by our solution method because, besides exceeding budget constraints, it contains some players which were bought by actual Serie A teams during the winter market season, therefore did not have a past history that allowed projections onto the future.

Table 3 Comparison of best teams
Full size table

Table 3 reports the results of this best teams league, this time with averages over 10 repetitions. The worthwhile element is that the expensiveTeam performed very well, as expected, but teams resulting from the suggestions of our support system proved able to be competitive and even in one case to beat it on average.

7 Conclusions

This work reports about a system to support bidders at fantasy football draft auctions. The system includes both a prescriptive and a predictive analytics module. Predictive analytics is based on an integer programming formulation of the problem the bidder must solve, that is relaxed in a Lagrangian fashion so that a simple matheuristic, compatible with mobile phone platforms, can quickly provide and update solutions. The proposed architecture can thus support adaptive, online decisions for each next bid.

The draft suggestions are based on the computation, for each available player having a sufficient past history in the national top league, of its Sharpe’s index (or Information Ratio), an index drawn from the financial literature for assessing different investment options. The index is in turn computed on the basis of forecasts of each player’s performance.

To validate the effectiveness of the suggestions, we implemented different leagues where teams drafted using different forecast algorithms and different available budgets were opposed. Computational results not only show that the system can effectively take advantage of increasing budget availabilities, but that it is also able to propose teams that prove effective even against a team socially deemed of higher global quotation, and including players that could not have been suggested due to insufficient past history for reliable forecasts.