Skip to main content
SpringerLink
Log in

A Constructive Methodology to Solving the Capacitated Newsvendor Problem: an Approximate Approach

  • Original Research
  • Published:
SN Operations Research Forum Aims and scope Submit manuscript

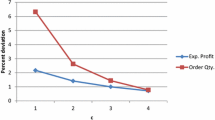
Abstract

The applications of the capacitated newsvendor problem are numerous. They range from inventory control, supply chain management, and airlines seat reservation to stock market applications. While several solution methodologies exist for this problem, most of them require advanced mathematical programming techniques or specifically developed iterative models. To complement these solution approaches and facilitate wider dissemination of this model particularly to upper-undergraduate and first-year graduate students as well as practitioners in related fields, in this paper, we develop an approximate solution methodology that is based on constructive approaches. These approaches already exist in standard textbooks of operations research, management science, and other similar disciplines. The two models utilized in the development are the classical newsvendor and the network flow model. Numerical comparisons are drawn between existing solution methodologies and the developed ones. Also, an example is presented to show the steps of the developed methodology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Hadley G, Whitin T (1963) Analysis of inventory systems. Englewood Cliffs, Prentice-Hall

    Google Scholar 

  2. Aloi G, Musmanno R, Pace P, Pisacane O (2012) A wise cost-effective supplying bandwidth policy for multilayer wireless cognitive networks. Comput Oper Res 39(11):2836–2847. https://doi.org/10.1016/j.cor.2012.02.016

    Article  Google Scholar 

  3. Fan J, Li K (2010) System and method for entity selection optimization. US 7783533 B1, United States Patent and Trademark Office

  4. Khouja M, Liu X, Zhou J (2020) To sell or not to sell to an off-price retailer in the presence of strategic consumers. Omega 90. https://doi.org/10.1016/j.omega.2018.11.011

  5. Hillier FS, Lieberman GJ (2015) Introduction to operations research. McGraw Hill, New York

    Google Scholar 

  6. Choi TM (2012) Handbook of newsvendor problems, International Series in Operations Research & Management Science, 176. Springer Science+Business Media, New York. https://doi.org/10.1007/978-1-4614-3600-3

  7. Gallego G, Moon I (1993) The distribution free newsboy problem: review and extensions. J Oper Res Soc 44(8):825–834. https://doi.org/10.1057/jors.1993.141

    Article  Google Scholar 

  8. Khouja M (1999) The single-period (newsvendor) problem: literature review and suggestions for future research. Omega 27(5):537–553. https://doi.org/10.1016/S0305-0483(99)00017-1

    Article  Google Scholar 

  9. Larissa J, Thorsten C, Jürgen S (2016) Literature review of deteriorating inventory models by key topics from 2012 to 2015. Int J Prod Econ 182:86–112. https://doi.org/10.1016/j.ijpe.2016.08.019

    Article  Google Scholar 

  10. Lau HS, Lau AHL (1995) The multi-product multi-constraint newsboy problem: applications, formulation and solution. J Oper Manag 13(2):153–162. https://doi.org/10.1016/0272-6963(95)00019-O

    Article  Google Scholar 

  11. Lau HS, Lau AHL (1996) The newsstand problem: a capacitated multiple-product single-period inventory problem. Eur J Oper Res 94:29–42. https://doi.org/10.1016/0377-2217(95)00192-1

    Article  Google Scholar 

  12. Abdel-Malek L, Montanari R (2005) An analysis of the multi-product newsboy problem with a budget constraint. Int J Prod Econ 97(3):296–307. https://doi.org/10.1016/j.ijpe.2004.08.008

    Article  Google Scholar 

  13. Niederhoff JA (2007) Using separable programming to solve the multi-product multiple ex-ante constraint newsvendor problem and extensions. Eur J Oper Res 176(2):941–955. https://doi.org/10.1016/j.ejor.2005.09.046

    Article  Google Scholar 

  14. Abdel-Malek L, Areeratchakul N (2007) A quadratic programming approach to the multi-product newsvendor problem with side constraints. Eur J Oper Res 176(3):1607–1619. https://doi.org/10.1016/j.ejor.2005.11.002

    Article  Google Scholar 

  15. Zhang B, Xu X, Hua Z (2009) A binary solution method for the multi-product newsboy problem with budget constraint. Int J Prod Econ 117(1):136–141. https://doi.org/10.1016/j.ijpe.2008.10.003

    Article  Google Scholar 

  16. Abdel-Malek L, Otegbeye M (2013) Separable programming/duality approach to solving the multi-product newsboy/gardener problem with linear constraints. Appl Math Model 37(6):4497–4508. https://doi.org/10.1016/j.apm.2012.09.059

    Article  Google Scholar 

  17. Abdel-Malek L, Montanari R, Meneghetti D (2008) The capacitated newsboy problem with random yield: the gardener problem. Int J Prod Econ 115:113–127. https://doi.org/10.1016/j.ijpe.2008.05.003

    Article  Google Scholar 

  18. Shi J, Zhang G, Sha J (2011) Jointly pricing and ordering for a multi-product multi-constraint newsvendor problem with supplier quantity discounts. Appl Math Model 35(6):3001–3011. https://doi.org/10.1016/j.apm.2010.12.018

    Article  Google Scholar 

  19. Dash JK, Sahoo A (2015) Optimal solution for a single period inventory model with fuzzy cost and demand as a fuzzy random variable. J Intell Fuzzy Syst 28(3):1195–1203. https://doi.org/10.3233/IFS-141402

    Article  Google Scholar 

  20. Wang D, Qin Z, Kar S (2015) A novel single-period inventory problem with uncertain random demand and its application. Appl Math Comput 269:133–145. https://doi.org/10.1016/j.amc.2015.06.102

    Article  Google Scholar 

  21. Moon I, Yoo DK, Saha S (2016) The distribution-free newsboy problem with multiple discounts and upgrades. Math Probl Eng 2016:1–11. https://doi.org/10.1155/2016/201725

    Article  Google Scholar 

  22. Areerakulkan N (2017) Quadratic approximation of the newsvendor problem with imperfect quality. J Rev Global Econ 6(2):335–341. https://doi.org/10.6000/1929-7092.2017.06.34

    Article  Google Scholar 

  23. Ravindra KA, Thomas LM, James BO (1993) Network flows: theory, algorithms and applications. Prentice-Hall, Englewood Cliffs, pp 296–298

    Google Scholar 

Download references

Acknowledgments

It would be remiss if we do not express our sincere appreciation for the invaluable feedback of two anonymous reviews.

We would also like to acknowledge the participation of the many students who contributed to make this paper possible.

Funding

This study has not received any external funding.

Author information

Authors and Affiliations

  1. Department of Mechanical and Industrial Engineering, New Jersey Institute of Technology, Newark, NJ, 07102, USA

    Layek Abdel-Malek & Pinyuan Shan

  2. Dipartimento di Ingegneriae Architettura, Università di Parma, Viale delle Scienze, 43100, Parma, Italy

    Roberto Montanari

Authors
  1. Layek Abdel-Malek
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pinyuan Shan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Roberto Montanari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Layek Abdel-Malek.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Appendix

Appendix

Fig. 4
figure 4

Flow chart exhibiting the steps of the proposed methodology

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abdel-Malek, L., Shan, P. & Montanari, R. A Constructive Methodology to Solving the Capacitated Newsvendor Problem: an Approximate Approach. SN Oper. Res. Forum 1, 8 (2020). https://doi.org/10.1007/s43069-020-0008-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s43069-020-0008-7

Keywords

Search

Navigation