One- and Multi-dimensional CWENOZ Reconstructions for Implementing Boundary Conditions Without Ghost Cells

Abstract

We address the issue of point value reconstructions from cell averages in the context of third-order finite volume schemes, focusing in particular on the cells close to the boundaries of the domain. In fact, most techniques in the literature rely on the creation of ghost cells outside the boundary and on some form of extrapolation from the inside that, taking into account the boundary conditions, fills the ghost cells with appropriate values, so that a standard reconstruction can be applied also in the boundary cells. In Naumann et al. (Appl. Math. Comput. 325: 252–270. https://doi.org/10.1016/j.amc.2017.12.041, 2018), motivated by the difficulty of choosing appropriate boundary conditions at the internal nodes of a network, a different technique was explored that avoids the use of ghost cells, but instead employs for the boundary cells a different stencil, biased towards the interior of the domain. In this paper, extending that approach, which does not make use of ghost cells, we propose a more accurate reconstruction for the one-dimensional case and a two-dimensional one for Cartesian grids. In several numerical tests, we compare the novel reconstruction with the standard approach using ghost cells.

Introduction

Computing, in an efficient way, accurate albeit non-oscillatory solutions of conservation laws requires the employment of high-order accurate numerical schemes. Their design encounters the main difficulties in controlling spurious oscillations near discontinuities and near the domain boundaries. The first problem is well tackled by reconstructions of the weighted essentially non-oscillatory ($\mathsf {WENO}$) class introduced in (see the reviews [36,37,38]) or by the central weighted essentially non-oscillatory [35] setting ($\mathsf {CWENO)}$ [1, 6, 23, 32, 44]. Results about the parameters and the accuracy of $\mathsf {CWENO,}$ $\mathsf {CWENOZ}$ and $\mathsf {CWENOZ\text{- }AO}$ class reconstructions in various finite volume settings are proven in [13, 15, 33].

The issue of boundary treatment for hyperbolic conservation laws is usually tackled by constructing ghost points or ghost cells outside the computational domain and by setting their values with suitable extrapolation techniques. Thanks to the ghost cells, a high-order non-oscillatory reconstruction procedure can be applied also close to the boundary even when its stencil is large. This approach is of course delicate, especially with finite-difference discretizations on non-conforming meshes. In this context, a very successful technique is the inverse Lax-Wendroff approach, which was introduced in [40], rendered more computationally efficient in [41], and further studied and extended for example in [24, 27, 28]; a quite up-to-date review may be found in [39]. A modified procedure enhancing its accuracy and stability has been proposed in [43]. Other approaches, still based on an inverse Lax-Wendroff procedure but tailored to coupling conditions on networks can be found in [7, 11]. A different approach, entirely based on $\mathsf {WENO}$ extrapolation is studied in [2, 3].

In [29] a different strategy was considered. There, in a one-dimensional finite volume context, ghost values are entirely avoided and the point value reconstruction at the boundary is performed with a $\mathsf {CWENO\ }$ type reconstruction that makes use only of interior cell averages. The reconstruction stencil for the last cell at the boundary is not symmetric, but extends only towards the interior of the computational domain. Then the boundary flux is determined from the reconstructed value and the boundary conditions.

In [29], achieving non-oscillatory properties when a discontinuity is close to the boundary requires the inclusion of very low degree polynomials (down to a constant one, in fact) in the $\mathsf {CWENO\ }$ procedure. This, in turn, calls for infinitesimal linear weights not to degrade the accuracy on smooth solutions. This type of CWENO reconstructions has been studied in general in [33] and is known as adaptive order $\mathsf {CWENO(Z)}$ ($\mathsf {CWENO\text{-}AO}$ or $\mathsf {CWENOZ\text{-}AO}$).

In this paper, we first enhance the accuracy of the boundary treatment of [29] by employing an adaptive order $\mathsf {CWENOZ\ }$ reconstruction from [33] and furthermore extend it to two space dimensions. In particular, in Sect. 2 we describe the new one-dimensional reconstruction that avoids ghost cells and, in Sect. 3, we compare it with the one of [29] with the aid of numerical tests. The novel two-dimensional no-ghost reconstruction is then presented in Sect. 4 and the corresponding numerical results are presented in Sect. 5 where we compare it with the ghosted approach of [15]. Some final remarks and conclusions are drawn in Sect. 6.

The Novel CWENOZb Reconstruction in One Space Dimension

We start recalling here the operators that define a generic $\mathsf {CWENO\ }$ reconstruction, which will be useful later.

Central $\mathsf {WENO}$ is a procedure to reconstruct point values of a function from its cell averages; it is different from the classical $\mathsf {WENO}$ by the fact that it performs a single nonlinear weight computation per cell and outputs a polynomial globally defined in the cell, which is later evaluated at reconstruction points.

In defining a $\mathsf {CWENO\ }$ reconstruction, one starts selecting an optimal polynomial, denoted here by $P_{\mathsf{\mathrm{opt}}}$, which should be chosen to have the maximal desired accuracy; the $\mathsf {CWENO\ }$ reconstruction polynomial, in fact, will be very close to $P_{\mathsf{\mathrm{opt}}}$ when the cell averages in the stencil are a sampling of a smooth enough function.

For the cases when a discontinuity is present in the stencil of $P_{\mathsf{\mathrm{opt}}}$, a sufficient number of alternative polynomials, $P_1,\cdots ,P_m$, typically with lower degree and with a smaller stencil, should be made available to the $\mathsf {CWENO\ }$ blending procedure. The $\mathsf {CWENO\ }$ operator then computes a nonlinear blending of all polynomials as follows. First a set of positive linear or optimal coefficients is chosen, with the only requirement that $d_{0}+d_1+\cdots +d_m=1$ and $d_i > 0, \; \forall i$. Then, the reconstruction polynomial is defined by

$$\begin{aligned} P_{\mathsf{\mathrm{rec}}}{=\mathsf {CWENO(}P_{\mathsf{\mathrm{opt}}};P_1,\cdots ,P_m)} = \omega _0\left( \frac{P_{\mathsf{\mathrm{opt}}}-\sum _{i=1}^{m}d_iP_i}{d_{0}}\right) +\sum _{i=1}^{m}\omega _iP_i \end{aligned}.$$

(1)

The quantities $\omega _i$ appearing above are called nonlinear weights; when $\omega _i\approx d_i$ for $i=0,\cdots ,n$, then $P_{\mathsf{\mathrm{rec}}}\approx P_{\mathsf{\mathrm{opt}}}$ and the reconstruction will have the maximal accuracy. When a discontinuity is present in the stencil, the nonlinear weights should deviate from their optimal values in order to avoid the occurrence of spurius oscillations in the numerical scheme. In practice, the nonlinear weights are computed with the help of oscillation indicators associated to each polynomial, that should be o(1) when the polynomial interpolates smooth data and ${\mathcal {O}}(1)$ when the polynomial interpolates discontinuous data. The construction is independent from the specific form of these indicators, which here we denote generically as $\mathrm {OSC}[P]$; typically the Jiang-Shu indicators from [21] are employed.

Let $\mathsf {CWENO(}P_{\mathsf{\mathrm{opt}}};\,P_1,\cdots ,P_m)$ denote the CWENO reconstruction based on the optimal polynomial $P_{\mathsf{\mathrm{opt}}}$ and on the polynomial of lower degree $P_1,\cdots ,P_m$. The nonlinear coefficients are computed as in the original WENO construction, namely as

$$\begin{aligned} \alpha _k = \frac{d_k}{\left( {\mathrm {OSC}[P_k]}+\epsilon \right) ^p}, \qquad \omega _k = \frac{\alpha _k}{\sum _j \alpha _j} \end{aligned},$$

(2)

where $\epsilon$ is a small parameter and $p\geqslant 1$. For detailed results on the accuracy of such a reconstruction, see [13] and the references therein.

Better accuracy on smooth data, especially on coarse grids, without sacrificing the non-oscillatory properties, can be obtained by computing the nonlinear weights as in the $\mathsf {WENOZ}$ construction of [16], namely as

$$\begin{aligned} \alpha _k = d_k\left[ 1+ \left( \frac{\tau }{{\mathrm {OSC}[P_k]}+\epsilon }\right) ^p\right], \qquad \omega _k = \frac{\alpha _k}{\sum _j \alpha _j}. \end{aligned}$$

(3)

In this case, we denote the reconstruction as $\mathsf {CWENOZ(}P_{\mathsf{\mathrm{opt}}};\,P_1,\cdots ,P_m)$. Here above, $\tau$ is a quantity that is supposed to be much smaller than the individual indicators when the data in the entire reconstruction stencil are smooth enough. For efficiency, this global smoothness indicator should be computed as a linear combination of the other oscillators. For results on the optimal choices for $\tau$ in a $\mathsf {CWENO\ }$ setting and the accuracy of the resulting reconstructions, see [15] and the references therein.

The accuracy results of both $\mathsf {CWENO\ }$ and $\mathsf {CWENOZ\ }$ require that certain relations among the accuracy of all polynomials involved are satisfied; the precise conditions for optimal accuracy depend also on the parameters $\epsilon$ and p [13, 15], but as a rule of thumb one should always have $\mathrm {deg}(P_{\mathsf{\mathrm{opt}}})\leqslant 2\mathrm {deg}(P_k)$ for $k=1,\cdots ,m$. If controlling spurious oscillations requires the inclusion in the nonlinear combination of polynomials with degree smaller than $\frac{1}{2}\mathrm {deg}(P_{\mathsf{\mathrm{opt}}})$, optimal accuracy can still be achieved. However, the linear weights of these additional polynomials of very low degree must be infinitesimal, i.e., chosen as ${\mathcal {O}}({\Delta }x^r)$ for some $r>0$. In order to easily distinguish the polynomials with infinitesimal linear weights, we adopt for this case the notations $\mathsf {CWENO\text{-}AO}(P_{\mathsf{\mathrm{opt}}};\,P_1,\cdots ,P_m;Q_1,\cdots ,Q_n)$, when (2) is used for the nonlinear weights, and $\mathsf {CWENOZ\text{-}AO}(P_{\mathsf{\mathrm{opt}}};\,P_1,\cdots ,P_m;Q_1,\cdots ,Q_n)$, when (3) is used instead. This approach was studied on a specific example in [29] for the $\mathsf {CWENO\ }$case and in general for $\mathsf {CWENOZ\text{-}AO}$ in [33]. This latter contains a thorough study of sufficient conditions on r and on the other parameters that guarantee optimal convergence rates for a generic $\mathsf {CWENOZ\text{-}AO}$ reconstruction.

Third-Order $\mathbf {CWb3}$ Reconstruction of (Naumann, Kolb, Semplice; 2018)

A third-order accurate reconstruction that does not make use of ghost cells has been introduced in [29]. The reconstruction coincides with the $\mathsf {CWENO3}$ reconstruction of [23] in the interior of the domain, with variable $\epsilon$ parameter as in [13, 14, 22]. In particular, for the j-th cell one considers the following polynomials: $P_j^{(2)}$, which is the optimal second degree polynomial interpolating $\overline{u}_{j-1},\overline{u}_j,\overline{u}_{j+1}$, $P^{(1)}_{j,L}$ and $P^{(1)}_{j,R}$, which are the linear polynomials interpolating $\overline{u}_{j-1},\overline{u}_j$ and $\overline{u}_j,\overline{u}_{j+1}$, respectively. $\mathsf {CWENO3}$ is a shorthand for $\mathsf {CWENO(}P_j^{(2)};\,P^{(1)}_{j,L},P^{(1)}_{j,R})$. This reconstruction produces a second degree, uniformly third-order accurate, polynomial defined in each cell, using the cell averages in a stencil of three cells. It can thus be computed on every cell in the domain except for the last one close to each boundary.

In the first cell of the domain, the reconstruction is replaced with an adaptive-order reconstruction $\mathsf {CWENO\text{- }AO}({\hat{P}}_1^{(2)};{P^{(1)}_{1,R}};\,P_1^{(0)})$ in which the stencils of the quadratic ${\hat{P}}_1^{(2)}$ and of the linear ${P^{(1)}_{1,R}}$ polynomial do not involve ghost cells (see also Fig. 1) and $P_1^{(0)}$ is the constant polynomial with value $\overline{u}_1$. In particular, ${\hat{P}}_1^{(2)}$ is the parabola that matches the cell averages $\overline{u}_1,\overline{u}_2,\overline{u}_3$ on the first three cells of the computational domain. After choosing linear coefficients $d^{(2)},d^{(1)},d^{(0)}$ for ${\hat{P}}_1^{(2)}, P^{(1)}_{1,R}, P_1^{(0)}$, respectively, the nonlinear weights are then computed with equations (2) and the reconstruction polynomial is finally given by (1). The last cell is treated symmetrically. In this paper we will refer to this reconstruction as $\mathsf {CWb3}$.

The inclusion of the constant polynomial $P^{(0)}$ is necessary to prevent oscillations when a discontinuity is present one cell away from the boundary and giving it an infinitesimal linear weight is necessary to guarantee the optimal order of convergence for the reconstruction procedure on smooth data. More precisely, in [29] it is shown that choosing the linear weights as $d^{(0)}=\min \left( {\Delta }x^{{\hat{m}}},0.01\right)$ for the constant polynomial, $d^{(1)}=0.25$ for the linear one and consequently setting $d_0=1-d^{(1)}-d^{(0)}$, guarantees the optimal accuracy on smooth data when ${\hat{m}}\in [1,2]$, provided $\epsilon ={\Delta }x^q$ with $q\geqslant {\hat{m}}$.

In general, a small $\epsilon$ yields good results on discontinuities, but keeping $q=1$ seems desirable to avoid rounding problems in the computation of the nonlinear weights. The combination ${\hat{m}}=2$ and $q=1$, does not fulfill the hypotheses of the convergence result for $\mathsf {CWb3}$ proven in [29]; in practice, however, the reconstruction appears to give rise nevertheless to a third-order accurate scheme but degraded accuracy can be observed at low grid resolutions. As an extreme example in this sense, let us consider the linear transport of a periodic initial datum in a periodic domain. Of course there would be no need to employ the no-ghost reconstruction in this case, since it would be trivial to fill in the ghost values (except maybe for considerations on parallel communication), but this example serves quite well to illustrate the situation on smooth data.

In Table 1 we report the 1-norm errors observed for the transport of $u(x,0)=\sin (\uppi x - \sin (\uppi x)/\uppi )$ after one period (for full details on the numerical scheme, the reader is referred to the beginning of Sect. 3). It is evident that for $\mathsf {CWb3}$, for $d^{(0)}\sim {\Delta }x^2$, the optimal rate predicted by the theory is observed in practice already on coarse grids; when $d^{(0)}\sim {\Delta }x$, instead third-order error rates can still be observed but only on very fine grids; in any case, the errors on coarse grids are still larger than its ghosted $\mathsf {CWENO3}$ counterpart.

Table 1 Errors on the linear transport of $\sin (\uppi x - \sin (\uppi x)/\uppi )$ in a periodic domain, using $\mathsf {CWENO3}$ and $\mathsf {CWb3}$ reconstructions $\left( \epsilon ={\Delta }x^2\right)$

The Novel $\,\,\,\,\,\mathbf {CWZb3}\,\,\,\,\,$ Reconstruction

The loss of accuracy at low grid resolution can be traced back to the relative inability of the smoothness indicators alone to detect a smooth flow on coarse grids. The net effect is that, when the grid is coarse, the nonlinear weight of the constant polynomial in the first and last cells is larger than it should be strictly needed, degrading the accuracy of the reconstruction and of the scheme near the boundary; the errors are then propagated into the domain by the flow.

This issue can be successfully counteracted, even on coarse grids, by the employment of Z-weights in the construction. In fact, we recall that the idea behind $\mathsf {WENOZ}$, see [16], is to replace the standard $\mathsf {WENO}$ nonlinear weight computation (2) with (3) where the global smoothness indicator $\tau$ is supposed to be $\tau =o(I_k)$ if the cell averages represent a locally smooth data in the stencil. The improved performances of $\mathsf {WENOZ}$ over $\mathsf {WENO}$, and of $\mathsf {CWENOZ\ }$ over $\mathsf {CWENO\ }$ reconstructions are in fact linked to the superior ability of detecting smooth transitions, already at low-grid resolution, which is granted by the global smoothness indicator $\tau$. Moreover, detecting a smooth flow even at low-grid resolution depends on how small is $\tau$ on smooth data; thus the goal in the optimal design of $\tau$ is to choose the coefficients of the linear combination $\lambda _0\mathrm {OSC}[P_{\mathsf{\mathrm{opt}}}]+\sum _{i=1}^{n}\lambda _k\mathrm {OSC}[P_k] = {\mathcal {O}}({\Delta }x^s)$ that maximize s when the data in the stencil of the reconstruction are a sampling of a smooth function [15].

Fig. 1

Illustration of the stencil for the third-order reconstruction in the last cell. Blue: cell where the reconstruction is computed. Black: the polynomials involved in $P_{\mathsf{\mathrm{rec}}}$. Gray: additional polynomial for $\tau _{(b3)}$

Our proposal thus consists in defining the new $\mathsf {CWZb3}$ reconstruction to coincide with $\mathsf {CWENOZ3}=\mathsf {CWENOZ} \big (P_j^{(2)};\,P^{(1)}_{j,L},P^{(1)}_{j,R}\big )$ in the domain interior, with the adaptive-order reconstruction $\mathsf {CWENOZ\text{- }AO}\big ({\hat{P}}_1^{(2)};\,P_{1,R}^{(1)};\,P_1^{(0)}\big )$ in the first cell and with $\mathsf {CWENOZ\text{- }AO}\big ({\hat{P}}_N^{(2)};\,P_{N,L}^{(1)};\,P_N^{(0)}\big )$ in the last cell.

To specify our choice of $\tau$, recall that the Jiang-Shu oscillation indicators [21] are defined as

$$\begin{aligned} \mathrm {OSC}[P] := \sum _{\ell \geqslant 1} {\Delta }x^{2\ell -1} \int _{\varOmega _j} \left( \frac{\mathrm {d}^{\ell }}{\mathrm {d}x^{\ell }} P \right) ^2 \mathrm {d}x, \end{aligned}$$

where $\varOmega _j$ is the cell where the reconstruction is applied. On smooth data,

$$\begin{aligned} \mathrm {OSC}\left[ P_j^{(2)}\right]&= \left( u'(x_j)\right) ^2 {\Delta }x^2 + {\mathcal {O}}\left( {\Delta }x^4\right), \\ \mathrm {OSC}\left[ P^{(1)}_{j,L}\right]&= \left( u'(x_j)\right) ^2 {\Delta }x^2 - u'(x_j)u''(x_j){\Delta }x^3 +{\mathcal {O}}\left( {\Delta }x^4\right), \\ \mathrm {OSC}\left[ P^{(1)}_{j,R}\right]&= \left( u'(x_j)\right) ^2 {\Delta }x^2 + u'(x_j)u''(x_j){\Delta }x^3 +{\mathcal {O}}\left( {\Delta }x^4\right) , \end{aligned}$$

so that the combination

$$\begin{aligned} \tau _j=\left| 2\mathrm {OSC}\left[ P_j^{(2)}\right] -\mathrm {OSC}\left[ P^{(1)}_{j,L}\right] -\mathrm {OSC}\left[ P^{(1)}_{j,R}\right] \right| \end{aligned}$$

(4)

is ${\mathcal {O}}\left( {\Delta }x^4\right)$; this very low $\tau$ biases very strongly the nonlinear weights (3) towards the optimal ones whenever the flow is smooth. In [15] it is shown that this is the optimal choice and that it is not possible to obtain a combination of the indicators that is $o({\Delta }x^4)$ in the third-order setup.

We now need to specify a suitable $\tau _1$ for the asymmetrical stencil of the first cell and $\tau _N$ for the last one. Recall that the role of $\tau$ is to indicate whether the data are smooth in the stencil, which is composed by the first three cells adjacent to the boundary. As argued in [33], only the polynomials with degree at least one are useful in the construction of $\tau$. One could use the oscillators of the parabola $P^{(2)}$ fitting the three cell averages $\overline{u}_1,\overline{u}_2,\overline{u}_3$ and the linear polynomial $P^{(1)}_1$ interpolating the first two,

$$\begin{aligned} \mathrm {OSC}\left[ {\hat{P}}^{(2)}_{1}\right]&= \left( u'(x_1)\right) ^2 {\Delta }x^2 + {\mathcal {O}}({\Delta }x^4),\\ \mathrm {OSC}\left[ P^{(1)}_{1,R}\right]&= \left( u'(x_1)\right) ^2 {\Delta }x^2 + u'(x_1)u''(x_1){\Delta }x^3 +{\mathcal {O}}\left( {\Delta }x^4\right), \end{aligned}$$

but then it is not possible to exploit the symmetry to obtain a global smoothness indicator of size ${\mathcal {O}}({\Delta }x^4)$.

Using $\tau _1={\mathcal {O}}\left( {\Delta }x^3\right)$, however, could make the reconstruction in the boundary cell less performing than the one in the domain interior. To overcome this difficulty, one could employ, in the construction of $\tau$, also the indicator of the linear polynomial ${\widetilde{P}}^{(1)}$ interpolating the averages $\overline{u}_2,\overline{u}_3$. However, since the role of $\tau$ is to detect smooth flows in the global stencil, which is composed by the first three cells and thus coincides with the stencil employed by the second cell, a simpler solution (which also allows to save some computations) is to take instead for the first cell the same value of $\tau$ that was computed in the second cell; this is ${\mathcal {O}}\left( {\Delta }x^4\right)$ on smooth flows and yields a better reconstruction.

The novel reconstruction procedure that we propose is thus:

• in all cells except the first and last one, compute the $\mathsf {CWENOZ3}$ reconstruction polynomial with the optimal definition (4) of $\tau _j$, as in [15];

• in the first cell, apply $\mathsf {CWENOZ\text{- }AO}\left( {\hat{P}}_1^{(2)};\,P_{1,R}^{(1)};\,P_1^{(0)}\right)$ with $\tau _1:=\tau _2;$

• in the last cell, apply $\mathsf {CWENOZ\text{- }AO}\left( {\hat{P}}_N^{(2)};\,P_{N,L}^{(1)};\,P_N^{(0)}\right)$ with $\tau _N:=\tau _{N-1}$.

After the analysis of §3.1.1 of [33], it is expected that this reconstruction has third order of accuracy for $d^{(0)}={\mathcal {O}}({\Delta }x)$ provided that $p\geqslant 1$ and $\epsilon ={\mathcal {O}}({\Delta }x^{{\hat{m}}})$ for ${\hat{m}}\in [1,3]$.

As discussed in [15], the choice of parameters within the allowed ranges can trade better accuracy on smooth flows (larger ${\hat{m}}$ or smaller q) with smaller spurious oscillations on discontinuities (smaller ${\hat{m}}$ or larger q). In [15] it was found that a good overall choice for $\mathsf {CWENOZ3}$ was $p=1$ and ${\hat{m}}=2$ and we will adopt these values in all our numerical tests. Regarding the infinitesimal linear weight, the choices $d^{(0)}={\Delta }x$ and $d^{(0)}={\Delta }x^2$ will be compared.

Fig. 2

Spectral properties of the numerical differentiation operator induced by the $\mathsf {CWENO\ }$ and $\mathsf {CWENOZ\ }$ reconstructions and their no-ghost counterparts. (Left) Diffusion error. (Right) Eigenvalues

In Fig. 2 we report some results on the spectral properties of the reconstructions studied in this paper. In particular, following the approach of [12], we study the discrete operator ${\hat{D}}_x$ that is obtained by the composition of a point value reconstruction and an upwind flux:

$$\begin{aligned} \left. {\hat{D}}_x(\overline{U})\right| _j = -\left( U_{j+\nicefrac {1}{2}}^- - U_{j-\nicefrac {1}{2}}^-\right) , \end{aligned}$$

where $U_{j\pm \nicefrac {1}{2}}^{-}$ denotes the reconstructed value at the left of the interfaces. ${\hat{D}}_x(\overline{U}(t))$ is the right-hand side of the evolution equation for the cell averages in a semidiscrete scheme for the linear advection equation. We fix a grid and form a matrix ${\mathbb {F}}$ setting its k-th column to be the Fourier transform of ${\hat{D}}_x\left( \overline{U}^{(k)}\right)$, where $\overline{U}^{(k)}$ denotes the cell averages of the k-th Fourier mode on the grid. The analysis of the diagonal of ${\mathbb {F}}$ allows to introduce approximate diffusion and dispersion errors of the ${\hat{D}}_x$. This is analogous to the diffusion-dispersion study of [30], but here we consider only the spatial derivative operator and not also the further nonlinear contributions of the Runge-Kutta scheme evolving the cell averages in time.

The diffusion error of different reconstructions is compared in the left panel of Fig. 2. It can be seen that for each pair of a ghosted reconstruction ($\mathsf {CWENO3}$ or $\mathsf {CWENOZ3}$) and its no-ghost counterpart ($\mathsf {CWb3}$ and $\mathsf {CWZb3}$ respectively), it has the same sign and approximately the same magnitude. In the right panel, we show the eigenvalues of the matrix ${\mathbb {F}}$ on a grid with 64 cells. We can observe that the two cases of $\mathsf {CWENOZ3}$ and $\mathsf {CWZb3}$ are very close to each other. We can thus infer that the stability and maximum CFL number are not affected by replacing the ghosted with the no-ghost reconstruction.

Fully Discrete Numerical Scheme

Our fully discrete numerical scheme is obtained with the method of lines, the local Lax-Friedrichs numerical flux, and the third-order TVD-RK3 scheme [17] in time. The $\mathsf {CWENO3}$ and the $\mathsf {CWENOZ3}$ reconstruction from cell averages in the first and last cells make use of one ghost cell outside each boundary, which is filled according to the boundary conditions before computing the reconstruction. In the same cells, the $\mathsf {CWb3}$ and the $\mathsf {CWZb3}$ reconstructions, instead, do not make use of ghost cells but extend their stencil inwards for one extra cell with respect to their ghosted counterparts.

In both cases, the flux on the boundary face is computed by applying the local Lax-Friedrichs numerical flux to an inner value determined by the reconstruction and an outer value determined by the boundary conditions. For example, let us focus on the right domanin boundary and let $U^-_{N+\nicefrac {1}{2}}$ be the value of the reconstruction polynomial of the N-th cell on its right boundary.

• Periodic boundary conditions are applied computing the boundary flux with ${\mathcal {F}}\left( U^-_{N+\nicefrac {1}{2}},U^+_{1-\nicefrac {1}{2}}\right)$, i.e., using as outer value the inner reconstruction on the left of the first computational cell.

• Dirichlet boundary conditions prescribing $u=g(t)$ at the boundary are applied using the numerical flux ${\mathcal {F}}\left( U^-_{N+\nicefrac {1}{2}},g(t_n+c_i{\Delta }t)\right)$, where $t_n$ is the time at the beginning of the current timestep and $c_i$ is the abscissa of the i-th stage of the Runge-Kutta scheme.

• Reflecting boundary conditions in gasdynamics employ ${\mathcal {F}}\left( U^-_{N+\nicefrac {1}{2}},U_{\text {out}}\right)$ where $U_{\text {out}}=\left( \rho ^-_{N+\nicefrac {1}{2}},-v^-_{N+\nicefrac {1}{2}},p^-_{N+\nicefrac {1}{2}}\right)$ where $\rho$, v and p denote the density, velocity and pressure of the gas, respectively.

We point out that a similar approach based on $\mathsf {CWENO\text{- }AO}$ reconstructions of higher orders could be employed to construct boundary treatments for higher order schemes.

One-Dimensional Numerical Tests

All tests in this section are conducted with the finite volume scheme described in Sect. 2.3. The CFL number is set to 0.45 in all tests. The numerical tests have been performed with the open-source code claw1dArena, see [34].

Linear Transport

Periodic solution We consider the linear transport equation $u_t+u_x=0$ in the domain $[-1,1]$ with periodic boundary conditions. We evolve the initial data $u_0(x)=\sin (\uppi x - \sin (\uppi x)/\uppi )$ for one period, using the $\mathsf {CWENOZ3}$ and $\mathsf {CWZb3}$ reconstructions. Note that $u_0$ has a critical point of order 1 (see [18]).

Table 2 Errors on the linear transport of $\sin (\uppi x - \sin (\uppi x)/\uppi )$ in a periodic domain, using $\mathsf {CWENOZ3}$ and $\mathsf {CWZb3}$ reconstructions

Table 2 shows that, as in [33], $\mathsf {CWZb3}$ can reach the optimal convergence rate already with $d^{(0)}\sim {\Delta }x$ and that the errors obtained without using ghosts are very close to those of the ghosted reconstruction $\mathsf {CWENOZ3}$. As already pointed out in [15], we observe that using Z-weights in $\mathsf {CWENO\ }$ yields lower errors compared to the companion reconstructions with the Jiang-Shu weights (compare Table 1).

Smooth solution with time-dependent Dirichlet data For this second test, we consider again the linear transport equation on the domain $[-1,1]$, but we apply time-dependent Dirichlet boundary data on the left (inflow) boundary imposing $u(-1,t)=0.25 - 0.5\sin (\uppi (1.0+t))$ and free-flow conditions on the (outflow) boundary at $x=1$. We start with $u_0(x)=0.25 + 0.5\sin (\uppi x)$ and compare the computed cell averages with the exact solution $u(t,x)=u_0(x-t)$. The final time is set to 1. This test was proposed in [40].

Table 3 Errors on the smooth linear transport test with time-dependent Dirichlet data

The results reported in Table 3 show that the $\mathsf {CWZb3}$ reconstruction yields third-order error rates already on coarse grids and with $d^{(0)}\sim {\Delta }x$. No advantage is seen for the choice $d^{(0)}\sim {\Delta }x^2$.

We point out, in this case, that it would not be straightforward to apply a reconstruction that makes use of ghost cells, like $\mathsf {CWENO3}$ or $\mathsf {CWENOZ3}$. In [9] it was observed that accuracy would be capped at second order if the ghost cell values for the i-th stage were to be set by reflecting the inner ones in the exact boundary data at time $t_n+c_i{\Delta }t$, where $c_i$ denotes the abscissa of the i-th stage of the Runge-Kutta scheme. In the same paper, a suitable modification of the boundary data preserving the accuracy of the Runge-Kutta scheme is proposed. On the other hand, we point out that with the $\mathsf {CWb3}$ and $\mathsf {CWZb3}$ reconstructions this issue of filling the ghost cells is not present and the exact boundary data can be employed in the numerical flux computation, without observing losses of accuracy.

Discontinous solution Next we consider the same setup of the previous test, but impose the boundary value

$$\begin{aligned} u(-1,t)= {\left\{ \begin{array}{ll} 0.25, &{} t \leqslant 1,\\ -1, &{} t>1, \end{array}\right. } \end{aligned}$$

thus introducing a jump in the exact solution at $t=1$, computing the flow until $t=1.5$. This test was proposed in [40].

Fig. 3

Solutions computed with 100 cells for the discontinuous linear transport test, using $\mathsf {CWENOZ3}$, $\mathsf {CWb3}$ and $\mathsf {CWZb3}$ reconstructions ($\epsilon ={\Delta }x^2$)

The results are shown in Fig. 3, where we compare the solution computed with $\mathsf {CWENOZ3}$ using ghosts and the no-ghost $\mathsf {CWb3}$ and $\mathsf {CWZb3}$. In the final solution, no difference can be seen in the corner point at $x=0.5$, which is originated by a continous but not differentiable boundary data. On the other hand, the numerical solution around the jump at $x=-\,\,0.5$, which is generated by the discontinuity in the boundary data, has slightly more pronounced oscillations when using $\mathsf {CWZb3}$ and $d^{(0)}={\Delta }x^2$ and a more smoothed profile when using $\mathsf {CWb3}$. $\mathsf {CWZb3}$ with $d^{(0)}={\Delta }x$ produces an almost idential solution to the one computed by the ghosted $\mathsf {CWENOZ3}$ reconstruction.

Burgers’ Equation

For a nonlinear scalar test, we consider the Burgers’ equation $u_t+(u^2/2)_x=0$ with initial data $u_0(x)=1-\sin (\uppi x)$ with periodic boundary conditions, so that a shock forms, travels to the right and is located exactly on the boundary at $t=1$.

Fig. 4

Burgers’ test with 25 cells at $t=1$

In Fig. 4 we compare the solutions computed with 25 cells. One can see that $\mathsf {CWZb3}$ computes a solution which is almost exactly superimposed on the $\mathsf {CWENOZ3}$, despite the fact that using the correct periodic ghost values should be an advantage in this test. The $\mathsf {CWb3}$ solution is slightly more diffusive and, both choices of $d^{(0)}$ yield similar solutions.

Euler Gas Dynamics

In this section, we consider the one-dimensional Euler equations of gas dynamics,

$$\begin{aligned} \partial _t \left( \begin{array}{l} \rho \\ \rho v \\ E \end{array}\right) + \partial _x \left( \begin{array}{c} \rho v \\ \rho v^2 + p \\ u(E+p) \end{array}\right) = 0, \end{aligned}$$

where $\rho$, v, p and E are the density, velocity, pressure and energy per unit volume, respectively. We consider the perfect gas equation of state $E = \frac{p}{\gamma -1} + \frac{1}{2} \rho v^2$ with $\gamma =1.4$.

Incoming wave from the left In this test, we consider a gas initially at rest, with $\rho =1, p=1, v=0$. Through a time-dependent Dirichlet boundary condition on the left, we introduce the following disturbance:

$$\begin{aligned} \rho (t,0)=1.0+\delta (t), \quad p(t,0)=1.0+\gamma \delta (t), \quad \delta (t)= {\left\{ \begin{array}{ll} 0.01(\sin (2\uppi t))^3, &{} t\in [0,0.5],\\ 0, &{} t>0.5. \end{array}\right. } \end{aligned}$$

The boundary introduces a smooth wave travelling right. Wall boundary conditions are imposed on the right and the final time is set at $t=1.25$, when the wave is being reflected back from the wall.

Fig. 5

Gasdynamics. Incoming wave test using 50 cells. The reference is computed with 10 000 cells and a second order TVD scheme with the minmod slope limiter

In Fig. 5 we report the solutions at time $t=1.25$ computed on 50 cells with the third-order ghosted and ghost-free reconstructions, together with a reference solution computed on 10 000 cells with a second-order TVD scheme with minmod slope limiter.

Spurious oscillations coming from the Dirichlet boundary conditions on the left side are completely absent when using $\mathsf {CWb3}$ or $\mathsf {CWZb3}$. Instead $\mathsf {CWENOZ3}$ produces a deep undershoot. Also, a slightly better resolution is observed near the top of the wave. Here again, we stress that the $\mathsf {CWb3}$ and the $\mathsf {CWZb3}$ solutions have been computed by entirely neglecting the boundary conditions in the reconstruction phase and passing the exact Dirichlet value at $t_n+c_i{\Delta }t$ to the numerical flux as outer data on the left boundary.

Sods Riemann problem with walls In this test, we use the initial data of the Sod problem, with the density, velocity and pressure set to (1, 0, 1) for $x<0.5$ and (0.125, 0, 0.1) for $x>0.5$. The computational domain is the unit interval as usual, but we impose wall boundary conditions on both sides.

Fig. 6

Sod test with wall boundary conditions: wave structure of the solution. Thin (green) lines represent rarefaction waves, solid thick (red) lines are shocks, dashed thick (blue) lines are contact discontinuities. The states between the waves are indicated in the graph, using primitive variables, as $(\rho ,v,p)$

In Fig. 6 we show the wave structure of the exact solution for $x>0.5$. This Riemann problem gives rise to a left-moving rarefation (thin lines), a right moving contact (thick dashed line) and a faster right moving shock (thick solid line). The solution at $t=0.2$ is still unaffected by the wall boundary conditions. The shock bounces back from the wall at $t\approx 0.285$, interacts with the contact wave at $t\approx 0.408$, giving rise to two shocks moving in opposite directions and to a slow, right-moving contact. This shock rebounces from the wall at $t\approx 0.490$ and later interacts with the contact at $t\approx 0.560$. The solution at $t=0.6$ is composed, from right to left, by a right-moving very weak shock (density jump of 0.04), a very slow contact wave moving rightwards with speed 0.012, a left moving shock (velocity $-\,\,1.13$), a slower left-moving shock (velocity $-\,\,0.677$) and finally by the rarefaction originated from the initial Riemann problem, which is at this time is bouncing back into the domain from the left wall (not shown in Fig. 6).

Fig. 7

Sod test with wall boundary conditions on 400 cells. The rarefaction in the "exact" solution at t = 0.6 is computed with $\Delta {x}=$1/10 000 and a linear reconstruction with a second-order TVD scheme with the minmod slope limiter

In Fig. 7 we show, in the left panel, the solution at time $t=0.2$, which is before the waves reach the wall; the expected solution is still unaffected by the wall. All three solutions are very close to each other and only a slight extra diffusion can be noticed for the reconstruction that is using the Jiang-Shu nonlinear weights instead of the Z-weights.

In the right panel of Fig. 7 we show the solution at $t=0.6$. We see the rarefaction wave, which is reflecting in the left wall, and all the discontinous waves described before. It can be appreciated that $\mathsf {CWZb3}$, without using ghost cells, computes almost the same solution as the ghosted $\mathsf {CWENOZ3}$. As in other tests, $\mathsf {CWb3}$ is more diffusive. The very weak shock is barely captured at this resolution. The local characteristic projection has been used in this computation to control spurious oscillations that would otherwise appear in the plateaux between the two left-moving shocks and the hump left of the contact.

Fig. 8

Sod test in 3D, with 400 cells. The reference is computed with 10 000 cells and a linear reconstruction with the minmod limiter

Finally, we consider the d-dimensional version of the same problem. Following [42], in spherical symmetry this amounts to adding to the Euler equations the source term $S(\rho ,u,p)=-\tfrac{d-1}{x}\left[ \rho u,\rho u^2, up\right] ^{{\mathsf {T}}}$. In particular in Fig. 8 we show the solution for $d=3$ at $t=0.5$ and at $t=0.65$. In this test, the source term contribution is computed in each cell with a two-point Gaussian quadrature, which is fed by the reconstructed values. We thus test the $\mathsf {CWENO}$-based reconstructions’ capability of easily computing reconstructed values inside the cells. For all waves, we observe again that $\mathsf {CWZb3}$ and $\mathsf {CWENOZ3}$ produce very similar solutions, with the no-ghost version $\mathsf {CWb3}$ being slightly more diffusive.

Two-Dimensional Scheme

Fig. 9

Stencils for the 2d reconstruction in the middle of the domain (left), at a domain edge (center) and at a domain corner (right)

In this section, we consider a two-dimensional conservation law $\partial _t u + \nabla \cdot \mathbf {f}(u) = 0$ and discretize it on a Cartesian grid, with cells of size ${\Delta }x$. We denote the cells as $\varOmega _{i,j}$, with the pair of integers (i, j) referring to their position in the grid. The semi-discrete formulation reads

$$\begin{aligned} \frac{\mathrm{d}\overline{U}_{i,j}}{\mathrm{d}t} = - \frac{1}{|\varOmega _{i,j}|} \int _{\partial \varOmega _{i,j}} \!\!\!\!\!\!\mathbf {f}(u(t,\gamma ))\cdot \mathbf {n}(\gamma )\mathrm {d}\gamma , \end{aligned}$$

where $\overline{U}_{i,j}(t)$ is the cell average at time t in cell $\varOmega _{i,j}$. The solution is advanced in time with the third order TVD-SSP Runge-Kutta scheme [17]. At each stage, the integral of the flux is split in the contributions of each edge of the cell $\varOmega _{i,j}$ and each of them in turn is approximated with the two-point Gaussian quadrature of order 3. The eight quadrature points, in the reference geometry $[0,1]^2$, are located at $\{0,1\}\times \{\nicefrac 12\pm \nicefrac {\sqrt{3}}{6}\}$ and at $\{\nicefrac 12\pm \nicefrac {\sqrt{3}}{6}\}\times \{0,1\}$. At each quadrature point, a two-point numerical flux ${\mathcal {F}}\left( U_{\text {in}}, U_{\text {out}} \right)$, is applied to the inner and outer reconstructed values. On domain boundaries, only the inner point value, $U_\text {in}$, is computed by the reconstruction procedure, while $U_\text {out}$ is computed according to the boundary conditions similarly to the one-dimensional case. For Euler gas-dynamics, at a solid wall boundary, all components of $U_\text {out}$ are equal to those in $U_\text {in}$, except for the normal velocity, which is given the opposite sign.

The reconstruction from cell averages to point values in two space dimensions is not obtained by dimensional splitting, but is computed by blending polynomials in two spatial variables with a $\mathsf {CWENOZ\ }$ or a $\mathsf {CWENOZ\text{-}AO}$ construction. The reconstruction operator is called only once per cell per stage value and the polynomial returned is later evaluated at the eight reconstruction points where the numerical fluxes have to be computed.

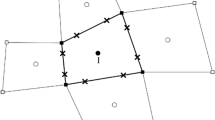
Let $\varOmega _{i,j}$ be the cell in which the reconstruction is being computed. In every cell, the reconstruction is computed by a $\mathsf {CWENOZ\ }$ operator with optimal polynomial $P_{\mathsf{\mathrm{opt}}}$ of degree two in two spatial variables (six degrees of freedom) associated with a $3\times 3$ stencil containing $\varOmega _{i,j}$ (see later for the definition of the polynomial associated to a stencil). The reconstruction stencils are depicted in Fig. 9. In all panels, the cell in which the reconstruction is being computed is hatched, while the stencil of the optimal polynomial of degree two is shaded.

The $\mathsf {CWENOZ\ }$ operator is fully specified after the low degree polynomials and the global smoothness indicator $\tau$ is also chosen. In Fig. 9, the stencils of the first-degree polynomials in two or one variables are indicated by circles joined by solid or dashed lines respectively; while polynomials of zero degree are indicated by a solid dot. Here below we describe how these polynomials are computed.

In the bulk of the computational domain, the reconstruction coincides with the two-dimensional $\mathsf {CWENOZ3}$ described in [15]; it is defined as a nonlinear combination of second- and first-degree polynomials as

$$\begin{aligned} \mathsf {CWENOZ(}P_{\mathsf{\mathrm{opt}}};\,P_{\mathsf {ne}},P_{\mathsf {se}},P_{\mathsf {sw}},P_{\mathsf {nw}}). \end{aligned}$$

The optimal polynomial is associated with the $3\times 3$ stencil of cells centered at $\varOmega _{i,j}$ (left panel in Fig. 9). The four polynomials $P_{\mathsf {ne}},P_{\mathsf {se}},P_{\mathsf {sw}}$ and $P_{\mathsf {nw}}$ are linear polynomials in two variables associated to the four stencils depicted with solid blue lines in the figure. For example, $P_{\mathsf {ne}}$ is associated to the stencil composed by the cells $\varOmega _{r,s}$ for $r\in \{i,i+1\}$ and $s\in \{j,j+1\}$. As in [15], we define the global smoothness indicator by

$$\begin{aligned} \tau = \big | 4\mathrm {OSC}[P_{\mathsf{\mathrm{opt}}}] - \mathrm {OSC}[P_{\mathsf {ne}}] -\mathrm {OSC}[P_{\mathsf {se}}] - \mathrm {OSC}[P_{\mathsf {sw}}] - \mathrm {OSC}[P_{\mathsf {nw}}] \big |, \end{aligned}$$

where $\mathrm {OSC}[P]$ is the multi-dimensional Jiang-Shu smoothness indicator, as defined in [19]. The nonlinear weights are computed by (3) starting from the linear weights $d_{{\mathsf {0}}}=\nicefrac 34$ and $d_{\mathsf {ne}}=d_{\mathsf {se}}=d_{\mathsf {sw}}=d_{\mathsf {nw}}=\nicefrac {1}{16}$.

Next we consider the case of a cell adjacent to a domain boundary. We focus in particular on the case of the bottom boundary, which is depicted in the central panel of Fig. 9. Here the reconstruction is

$$\begin{aligned} \mathsf {CWENOZ(}P_{\mathsf{\mathrm{opt}}};\,P_{\mathsf {ne}},P_{\mathsf {nw}},{\widetilde{P}}_{{\mathsf {e}}},{\widetilde{P}}_{{\mathsf {w}}}), \end{aligned}$$

where $P_{\mathsf {ne}}$ and $P_{\mathsf {nw}}$ are defined as in the domain bulk. The stencil of $P_{\mathsf{\mathrm{opt}}}$ is biased towards the domain interior and more precisely it is composed by the cells $\varOmega _{r,s}$ for $r\in \{i-1,i,i+1\}$ and $s\in \{j,j+1,j+2\}$. The other two polynomials, ${\widetilde{P}}_{{\mathsf {e}}}$ and ${\widetilde{P}}_{{\mathsf {w}}}$ are degree one polynomials that depend only on the tangential variable, x in the example, and are constant in the direction normal to the boundary. Their stencils are indicated with dashed lines in the figure. The global smoothness indicator $\tau$ for the cell in the example is copied from the cell $\varOmega _{i,j+1}$. The linear weights are similar to the bulk case, i.e., $d_{{\mathsf {0}}}=\nicefrac 34$ and $d_{\mathsf {ne}}=d_{\mathsf {nw}}=d_{{\mathsf {e}}}=d_{{\mathsf {w}}}=\nicefrac {1}{16}$. The case of the other boundaries is obtained from this one by symmetry.

In our numerical experiments, we have noticed that choosing correctly the linear weights for the low-degree polynomials in the boundary cells is important to avoid spurious waves and features generated by an anomalous diffusion in the tangential direction; this latter would show up for example when choosing infinitesimal weights for the planes ${\widetilde{P}}_{{\mathsf {e}}}$ and ${\widetilde{P}}_{{\mathsf {w}}}$.

Finally we describe the reconstruction in a domain corner, focusing on the case of the south-west one, which is represented in the right panel of Fig. 9. Here, for stability purposes, we must include also a constant polynomial in the $\mathsf {CWENOZ\ }$ operator, denoted with ${\widetilde{P}}_{{\mathsf {c}}}$, to avoid spurious oscillations when a strong wave hits the corner. ${\widetilde{P}}_{{\mathsf {c}}}$ has of course the constant value coinciding with the cell average of the corner cell and its 1-cell stencil is represented by the filled circle in the picture. Following [33], we assign to the constant polynomial ${\widetilde{P}}_{{\mathsf {c}}}$ and to the ${\widetilde{P}}_{{\mathsf {e}}}$ and ${\widetilde{P}}_{{\mathsf {n}}}$ polynomials an infinitesimal weight of $d_{{\mathsf {c}}}=d_{{\mathsf {e}}}=d_{{\mathsf {n}}}={\Delta }x^{2}$ and the reconstruction in the south-west corner cell is

$$\begin{aligned} \mathsf {CWENOZ\text{-}AO}\left( P_{\mathsf{\mathrm{opt}}};{P_{\mathsf {ne}}};{\widetilde{P}}_{{\mathsf {e}}},{\widetilde{P}}_{{\mathsf {n}}},{\widetilde{P}}_{{\mathsf {c}}}\right) . \end{aligned}$$

The stencil of $P_{\mathsf{\mathrm{opt}}}$ is again biased towards the interior of the domain and is composed by the cells $\varOmega _{r,s}$ for $r\in \{i,i+1,i+2\}$ and $s\in \{j,j+1,j+2\}$. ${\widetilde{P}}_{{\mathsf {e}}}$, similarly to the previous case, is a degree one polynomial that is constant in the y direction, while ${\widetilde{P}}_{{\mathsf {n}}}$ is a degree one polynomial that is constant in the x direction. The global smoothness indicator $\tau$ for the cell in the example is copied from the cell $\varOmega _{i+1,j+1}$. The case of the other corners is obtained from this one by symmetry.

Also this two-dimensional reconstructions will be referred as $\mathsf {CWZb3}$ in the rest of the paper.

Associating a polynomial to a stencil The polynomials associated to the stencils are computed as follows. Let ${\mathcal {S}}$ be a collection of neighbours of the cell $\varOmega _{i,j}$ that includes the cell itself and let ${\Pi }\subset {\mathbb {P}}^d(x,y)$ be the subspace of the polynomials of degree d in two spatial variables where $P_{{\mathcal {S}}}$ is sought. If the stencil ${\mathcal {S}}$ contains as many cells as the dimension of ${\Pi }$, the polynomial $P_{{\mathcal {S}}}$ is the solution of the linear system composed by the equations $\langle P_{{\mathcal {S}}} \rangle _{r,s}=\overline{u}_{r,s}$ for all $(r,s)\in {\mathcal {S}}$, where the operator $\langle \cdot \rangle _{r,s}$ denotes the cell average of its argument over the cell $\varOmega _{r,s}$. In the examples above, all polynomials with a tilde in their name are computed in this way.

When the cardinality of ${\mathcal {S}}$ is larger than $\mathrm {dim}( {\Pi })$, we associate to ${\mathcal {S}}$ the solution of the following constrained least-squares problem:

$$\begin{aligned} P_{{\mathcal {S}}} = \arg \min \left\{ \sum _{(r,s) \in {\mathcal {S}}} \big \vert \langle P_{{\mathcal {S}}} \rangle _{r,s} - \overline{u}_{r,s} \big \vert ^2, \, \text {such that } P_{{\mathcal {S}}}\in {\Pi }, \langle P_{{\mathcal {S}}} \rangle _{i,j}= \overline{u}_{i,j} \right\}. \end{aligned}$$

(5)

In the examples above, $P_{\mathsf{\mathrm{opt}}},P_{\mathsf {ne}},P_{\mathsf {se}},P_{\mathsf {sw}},P_{\mathsf {nw}}$ are computed like this.

On Cartesian grids, the constrained least square problem can be easily turned into an unconstrained one by choosing a basis of $\Pi$ consisting of a constant function and of polynomials with zero cell average, which are thus orthogonal to the constant one. Explicit expressions for the coefficients of the polynomials in the domain interior can be found in [10].

We point out that a similar approach based on $\mathsf {CWENO\text{-}AO}$ reconstructions of higher orders could be employed to construct boundary treatments for higher order schemes, like the fourth-order accurate bidimensional $\mathsf {CWENO\ }$ of [10].

Two-Dimensional Tests

The numerical scheme has been implemented with the help of the PETSc libraries [4, 5] for grid management and parallel communications; the tests were run on a multi-core desktop machine equipped with an Intel Core i7-9700 processor and 64 Gb of RAM. We show the results obtained with the local Lax-Friedrichs numerical flux.

We consider the two-dimensional Euler equations of gas dynamics,

$$\begin{aligned} \partial _t \left( \begin{array}{l} \rho \\ \rho u \\ \rho v \\ E \end{array}\right) + \partial _x \left( \begin{array}{c} \rho u \\ \rho u^2 + p \\ \rho u v \\ u(E+p) \end{array}\right) + \partial _y \left( \begin{array}{c} \rho v \\ \rho u v \\ \rho v^2 + p \\ v(E+p) \end{array}\right) = 0, \end{aligned}$$

where $\rho$, u, v, p and E are the density, velocity in the x and y direction, pressure and energy per unit volume, respectively. We consider the perfect gas equation of state $E = \frac{p}{\gamma -1} + \frac{1}{2} \rho (u^2+v^2)$ with $\gamma =1.4$.

Convergence Test

We compare the novel reconstruction with the one of [15], that makes use of ghost cells, on the isentropic vortex test [35]. Of course there would be no need to use a ghost-less reconstruction with periodic boundary conditions, since it would be trivial to set up and fill in the ghost cells, but we conduct this as a stress test to verify the order of accuracy of the novel reconstruction.

The initial condition is a uniform ambient flow with constant temperature, density, velocity and pressure $T_\infty =\rho _\infty =u_\infty =v_\infty =p_\infty = 1.0$, onto which the following isentropic perturbations are added in velocity and temperature:

$$\begin{aligned} (\delta u, \delta v) = {\frac{\beta }{2 \uppi }} \exp \left( {\frac{1-r^2}{2}} \right) (-y,x), \quad \delta T = - { \frac{(\gamma - 1 ) \beta ^2}{8 \gamma \uppi ^2}} \exp \left( {1-r^2} \right) , \end{aligned}$$

where $r=\sqrt{x^2+y^2}$ and the strength of the vortex is set to $\beta =5.0$. The domain is the square $[-5,5]^2$ with periodic boundary conditions and the final time is set to $t=10$ so that the final exact solution is the same as the initial state.

Table 4 Errors on the isentropic vortex test, using $\mathsf {CWENOZ3}$ and $\mathsf {CWZb3}$ reconstructions

We observe third-order convergence rates in all variables (1-norm errors in density and energy are shown in Table 4). Compared with the $\mathsf {CWENOZ3}$ scheme, the errors are no worse, and in some cases slightly better.

Two-Dimensional Riemann Problem

We have run a number of Riemann problems, in particular configurations B, G and K from [31], to compare the performances of the novel reconstruction on flows with waves almost orthogonal to the boundary.

We point out that choices of linear weights for the boundary reconstructions departing from the ones described in Sect. 4 may lead to spurius tangential diffusion. (This latter would be observed for example when choosing infinitesimal weights for the planes with two cells in the stencil in the middle panel of Fig. 9). Since it is on contact waves that spurious diffusion can accumulate over time and become visible, we report only a comparison of the solutions computed with the ghosted and the no-ghost reconstructions on configuration B of [31], which involves four contact discontinuities.

Fig. 10

Two-dimensional Riemann problem with four slip lines, computed with (left) and without (right) ghost cells. The colorbar is for the pressure; there are 29 contour lines for the density, spaced by 0.1, from 0.25 (center of pictures) to 3.05 (near the bottom and right sides)

We evolved an initial configuration with constant data in the four quadrants; in particular, we set $p=1$ everywhere and

$$\begin{aligned} (\rho ,u,v)= \left\{ \begin{array}{c|c} \text {upper left} &{} \text {upper right} \\ (2.0,0.75,0.5) &{} (1.0,0.75,-0.5) \\ \hline (1.0,-0.75,0.5) &{} (3.0,-0.75,-0.5) \\ \text {lower left} &{} \text {lower right} \\ \end{array} \right\} \end{aligned},$$

so that the solution contains four contact waves rotating in the clock-wise direction. The domain is the square $[-0.5,0.5]^2$ with free-flow boundary conditions.

The solutions computed with and without ghost cells are shown in Fig. 10. In the plot, the colors stand for pressure (rainbow colorbar) and we are also showing contour lines of the density (grayscale colorbar). We are focusing on contact waves as they are a good indicator of numerical diffusion, since on this kind of waves its effects accumulate over time. No difference is visible between the two computed solutions, indicating that the no-ghost reconstruction does not introduce significant differences with respect to the standard approach that makes use of ghosts. In particular, no wave deformation is visible close to the boundary, indicating that, with our choice of linear weights, no extra tangential diffusion is introduced in the boundary cells.

Radial Sod Test

Next we run the cylindrical Sod shock tube problem in two space dimensions. The initial conditions for the velocity are $u,v=0$ everywhere, while density and pressure are $(\rho _H,p_H)=(1,1)$ for the central region, i.e., where $r=\sqrt{x^2+y^2}<0.5$, and $(\rho _L,p_L)=(0.125,0.1)$ elsewhere. We compute the solution only in the first quadrant of the domain, by setting the computational domain $\varOmega =[0;1]^2$, and using reflecting boundary conditions on all sides, representing symmetry lines along $x=0$ and $y=0$ and walls at $x=1$ and $y=1$.

Fig. 11

Radial Sod solutions at $t=0.2$

Fig. 12

Radial Sod solutions at $t=0.2$ with the no-ghost $\mathsf {CWZb3}$ reconstruction. Density as a function of the cell center from the origin for all cells. Whole solution (left), zoom on the contact (middle) and on the shock (right)

In Fig. 11 we compare the solutions at $t=0.2$ computed on a grid of $400\times 400$ cells, with and without ghost cells. As before, the pressure is in colour, while for the density 25 equispaced contour lines of the density field, from 0.04 to 1.0, are also shown (grayscale colorbar), so that the type of wave can be easily recognized. In all the pictures, the $\mathsf {CWENOZ3}$ solution is shown reflected to the left to ease the comparison.

Almost no difference can be appreciated between the two solutions and even the small artifacts appear identical in both schemes. Further, in Fig. 12, we plot the density computed without ghost cells as a function of the distance of the the cell center from the origin. An almost perfect radial symmetry is observed, despite the fact that the boundary cells are reconstructed with a different algorithm than the bulk ones.

Fig. 13

Radial Sod solutions at $t=6$

After $t=0.2$ the cylindrical shock wave interacts with the outer walls and later with the expanding contact. The reflected curved shock interacts with itself exactly at the upper-right corner at $t\simeq 0.56$; in Fig. 13, we show the solution at $t=0.6$, just after this event. In this way, we are testing the numerical schemes on reflecting a non-planar shock wave on a wall. Even more importantly, we are stressing the reconstruction procedure in the corner cell. In fact the shocks converge in the corner and therefore, for some timesteps, there is no smooth stencil available to the reconstruction procedure for the corner cell. Here too, no appreciable difference is visible between the solutions computed with the two reconstruction schemes, showing that not using ghost cells in the reconstruction does not impair the numerical scheme.

Implosion Problem

Next we consider the problem of a diamond-shaped converging shock proposed in [20]. As for the previous test, the solution is computed only in the first quadrant, with symmetry boundary conditions. This test stresses the non-oscillatory properties of the reconstruction in a corner cell: in fact here, at first an oblique shock interacts with the boundary for a long time, and later the four sides of the diamond shock converge in the origin and are reflected back from there.

The test is set in the square domain $[0,0.3]^2$ with reflective boundary conditions on all four sides: those at $x=0$ and $y=0$ represent symmetry lines, while the other two are physical solid walls. The initial condition has zero velocity everywhere and $\rho =1,p=1$ in the outer region ($x+y>0.15$) and $\rho =0.125,p=0.14$ in the interior one. A useful reference for this test is [26] and the first author’s website cited therein [25]. We show the solution computed with a grid of $800\times 800$ cells; the final time was set to $t=2.5$, saving snapshots every 0.005 until $t=0.1$ and every 0.1 afterwards.

Fig. 14

Implosion test at $t=0.03$. The rainbow colorbar is for the pressure, the grayscale one is for the density isolines. In the right panel, the arrows represent the velocity. In the left panel, the main shock (S), contact (C) and rarefaction (R) are indicated with capital letters, some secondary waves with small letters

Figure 14 shows both solutions in an early stage of the evolution, at $t=0.03$. Here and in all subsequent figures, we have mirrored to the left the solution computed with ghosts. In the early stages of the evolution the initial discontinuity gives rise to a shock (indicated with “S” in the left panel) and a contact (“C”), both moving towards the origin, and to a rarefaction (“R”) that moves outwards. At the boundary, the shock is reflected and the reflected waves interact with the incoming contact (“s” and “c” in the figure). In the right panel, the gas velocity is represented with arrows; notice the fast wind directed towards the origin blowing along the coordinate axis.

Fig. 15

Implosion test at $t=0.06$

Later the main shock and the reflected shocks converge in the origin, hit there head to head and are bounced back outwards. The snapshot reported in Fig. 15 is taken at $t=0.06$, just after this event. Here it is important to observe that no spurious waves and no difference among the two schemes can be observed close to the origin, testifying that the reconstruction procedure in the corner cells is able to employ correctly the constant polynomial when the waves are very close.

The reflected contact, further deformed by the interaction with the expanding reflected shock, is being deformed by the wind blowing along the coordinate axes; this is quite visible now at the point indicated by (a) in Fig. 15. Also this feature of the flow is computed symmetrically by both the ghosted and the no-ghost schemes.

Fig. 16

Implosion test at $t=0.1$

In Fig. 16 we show the solution at time $t=0.1$. At this time the rarefaction is still moving outwards, while the rounded shock bounced back from the origin has overcome the incoming contact, which correctly became unstable (see the wiggles along the front).

Fig. 17

Implosion test $t=2.5$. Note that this figure has a different colorbar than the previous ones

When the evolution is computed for long times, [26] demonstrates there is no consensus among the different schemes about the form of the bubbles near the origin and along the main diagonal. In Fig. 17 we report the solutions computed for $t=2.5$ (note the different pressure colorbar than in the previous plots). At this time, many waves reflections, refractions and interactions have taken place and the solution exhibit a quite complex pattern. The two schemes compute the main waves and the pressure field almost identically, but differ from each other in the bubbles, which appear to be physically unstable slip lines. It is quite natural that different schemes represent them in a different way.

Shock-Bubble Interaction

The last computation that we show is the shock-bubble interaction problem from [8]. Here a right-moving shock hits a standing bubble of gas at low pressure. In the computational domain $[-\,\,0.1, 1.6] \times [-\,\,0.5, 0.5]$, three distinct areas are considered: the post-shock region (A) for $x < 0$, the bubble (B) of center (0.3, 0.0) and radius 0.2 and the pre-shock region (C) of all points with $x > 0$ and not in (B). A sketch of the domain and the initial data are reported in Table 5. Boundary conditions are of Dirichlet type on the left (equal to the initial data), free-flow on the right, solid walls on $y = \pm 0.5$. The symmetry in the y variable permits a half domain computation (here $y > 0$) considering symmetry boundary conditions at $y = 0$.

Fig. 18

Shock-bubble test: at $t=0.4$. The top panel is colored by density. The bottom panel is a numerical Schlieren plot obtained by representing the magnitude of the density gradient in a grayscale logarithmic colorbar

Table 5 Domain and initial data for the shock-bubble problem

The shock, in its movement towards the right, sets in motion, compresses and deforms the bubble; the refracted shocks arising from the interaction of the main shock with the bubble are bounced back towards $y=0$ by the outer walls, giving rise to a very complex interaction pattern. The bubble is unstable and computing the solution with different schemes or different grid resolutions will give it different final shapes. In Fig. 18 we show the solutions at the final time of the computation, $t=0.4$; the $\mathsf {CWENOZ3}$ solution is mirrored in the symmetry axis to ease the comparison with the no-ghost solution computed with $\mathsf {CWZb3}$. Here the main difference can be seen in the portion of the bubble that remains attached to the symmetry plane. All the other waves, including the central portion of the bubble, are almost identical in both computations.

Conclusions and Perspectives

In this paper, we have pursued further the approach of [29] for reconstructions in finite volume schemes without using ghost cells. While the main motivation there was the application in internal nodes of networks, where it is difficult to prescribe appropriate extrapolations, here we have focused on the accuracy of the reconstructions and on the extension to higher dimensions. All the proposed reconstructions in the boundary cells are based on reconstruction stencils that are not symmetric (but extended only inwards) and nevertheless optimal accuracy on smooth flows can be achieved.

We suggested the employment of Z-weights instead of the Jiang-Shu nonlinear weights, obtaining a reconstruction that has less numerical diffusion than the one of [29]. Perhaps more importantly, the novel reconstruction can reach the optimal third-order convergence in an ample subset of the parameter space and in particular can employ a very small $\epsilon$ without needing the infinitesimal weight of the constant polynomial to be ${\mathcal {O}}({\Delta }x^2)$.

In the second part of the paper, we have proposed a reconstruction for two-dimensional Cartesian grids, which is fully 2D without dimensional splitting. This new boundary reconstruction has been compared with the $\mathsf {CWENOZ\ }$ approach of [15] that uses ghost cells, showing that the employment of ghost cells can be entirely avoided without affecting the quality of the computed solutions.

The approach without ghosts cells appears thus to be quite promising since setting them is always a tricky point in numerical schemes. It seems interesting to pursue further this line of research reaching higher accuracy with the help of higher order $\mathsf {CWENO\text{-}AO}$ reconstructions or applying it for moving boundaries as in piston problems.