A Multi-physics Methodology for Four States of Matter

Abstract

We propose a numerical methodology for the simultaneous numerical simulation of four states of matter: gas, liquid, elastoplastic solids, and plasma. The distinct, interacting physical processes are described by a combination of compressible, inert, and reactive forms of the Euler equations, multi-phase equations, elastoplastic equations, and resistive MHD equations. Combinations of systems of equations are usually solved by coupling finite element for solid modelling and CFD models for fluid modelling or including material effects through boundary conditions rather than full material discretisation. Our simultaneous solution methodology lies on the recasting of all the equations in the same, hyperbolic form allowing their solution on the same grid with the same finite volume numerical schemes. We use a combination of sharp- and diffuse-interface methods to track or capture material interfaces, depending on the application. The communication between the distinct systems of equations (i.e., materials separated by sharp interfaces) is facilitated by means of mixed-material Riemann solvers at the boundaries of the systems, which represent physical material boundaries. To this end, we derive approximate mixed-material Riemann solvers for each pair of the above models based on characteristic equations. To demonstrate the applicability of the new methodology, we consider a case study, where we investigate the possibility of ignition of a combustible gas that lies over a liquid in a metal container that is struck by a plasma arc akin to a lightning strike. We study the effect of the metal container material and its conductivity on the ignition of the combustible gas, as well as the effects of an additional dielectric coating, the sensitivity of the gas, and differences between scenarios with sealed and pre-damaged metal surfaces.

1 Introduction

The accurate numerical simulation of a wide range of manufacturing, automotive, aerospace, and defence processes necessitates the consideration of combinations of gases, liquids, elastoplastic solids, and plasma. Examples include prevention of ignition sources from entering an aircraft fuel tank containment system, and prevention of combustion of exposed ordnance and explosives in mining sites. Other examples include additive manufacturing processes such as laser melt of metal powder. This article presents numerical methods for the simultaneous solution of equations describing these four distinct states of matter, allowing the non-linear communication of the materials in a multi-physics framework. The methodology can also be used as part of the manufacturing process for optimising industrial components in terms of shapes and materials, e.g., for aeronautical wing coatings or automotive parts.

An integrated numerical methodology for simulating an application involving four states of matter has three elements; the formulations describing each state of matter, the numerical methods that solve these separately and the communication between any two models through material coupling. Here, we give an overview of relevant literature concerning the first and the last of these elements, as this is where the novelty of this work lies. In the rest of this section, we summarise the background literature of formulations modelling elastoplastic solids, plasma, and fluids (liquids and gases) and give an overview of existing communication methods between these.

The mathematical description of the elastoplastic system has been traditionally done in a Lagrangian framework. The original Lagrangian form of the solid equations has been reformulated into a conservative form of equations in the Eulerian frame by Godunov and Romenskii [21], Kondaurov [26] and Plohr and Sharp [43]. This has the advantage of allowing the solution of the elastoplastic solid formulation in the same framework as the hydrodynamic formulation for fluids, using the same (or the same family of) high-resolution, shock-capturing methods. This led to the development of high-order, shock-capturing schemes for the numerical solution of such systems. For example, Miller and Colella [35] and Barton et al. [7, 8] have developed linearised Riemann solvers as part of a high-order numerical scheme to capture the seven waves in the (1D) solid system, while Gavrilyuk et al. [20] have presented the adaptation of the classic HLLC solver to the solid system. Centred numerical schemes and linearised Riemann solvers for the solid systems have also been presented by Titarev [59], while approximate and exact Riemann solvers for the conservative elastic system have been presented by Miller [34] and Barton et al. [7].

Inclusion of plasticity in the solid system has been presented using different approaches, as, for example, by Miller and Colella [35], who evolve the plastic deformation gradient (${\mathbf {F}}^p$) in addition the total inverse deformation gradient (${\mathbf {G}}={\mathbf {F}}^{-1}$) and include an elastic predictor step followed by a “plastic” corrector step to correct any over-estimated elastic deformation that results in a state going beyond the yield surface. The predictor–corrector approach allows for solving both for perfect and time-dependent plasticity models. Another approach is followed by Barton et al. [8] who only evolve the elastic deformation gradient (${\mathbf {F}}^e$) and include plasticity as source terms for the elastic deformation tensor equations.

The full system for modelling resistive ionised material in the presence of electric and magnetic fields is the resistive MHD equations, which couple the Navier–Stokes equations to Maxwell’s equations. Using these to model lightning strike, or laboratory-based plasma arcs couples vastly different timescales; the electromagnetic effects have a characteristic timescale of the speed of light, while the mechanical dynamics of the system have a characteristic timescale of the speed of sound. Interesting numerical studies on lightning modelling include work by Plooster [44,45,46], Paxton et al. [42], Aleksandrov et al. [3], Tanaka et al. [57], Chemartin et al. [10, 12, 13], Villa et al. [61] and Tholin et al. [58].

The mathematical description of the fluids (liquid and gas) could vary in complexity, depending on the physical properties of the material that are dominant in the application of consideration. Formulations relevant to this work¹ include members of the Euler and augmented Euler class of conservation laws (e.g., [5, 6, 54,55,56, 62]), the BN type and reduced classes of conservation laws (e.g., [4, 24, 40, 50]) or hybrid formulations (e.g., [32, 53]).

Traditionally, solid–fluid coupling is done following Lagrangian techniques. These, however, present difficulties for large deformations of the materials as they are inherently translated to large deformations in the underlying mesh. Other methods for solid–fluid coupling include smoothed particle hydrodynamics (SPH) and arbitrary Lagrangian–Eulerian (ALE). In addition, in solid–fluid problems, it is common to use one-way coupling of finite element codes (describing the solid material) with CFD codes (modelling the fluid part). As a result, the two processes are solved in a “co-simulation” environment, each on its own grid with a distinct numerical method, without the non-linear interaction of the materials involved. This may also lead to discretisation errors passing from one method to the other. Studies including solid–fluid coupling in the Eulerian frame include work by Miller and Colella [36], Barton et al. [9], Schoch et al. [51] and De Brauer et al. [15], as well as Monasse [38] in an embedded boundary framework, Favrie et al. [16, 17] in a diffuse-interface approach and by Michael and Nikiforakis [33] in a combination of sharp- and diffuse-interface approaches. To the authors’ knowledge, the simultaneous solution of plasma arc and a solid has not been presented before. The interaction of the lightning arc with a surface (e.g.,  [1, 10,11,12,13, 19, 23, 25, 27, 41]) is usually done by considering prescribed plasma or prescribed material conductivity at the material interface rather than considering full solution of the two phases simultaneously.

The literature suggests that previous work or existing commercial codes used for multi-material and multi-phase applications can often only handle limited (less than four) combinations of states of matter. For lack of better methods, the trend is to do so using a combination of different codes in a “co-simulation” environment (e.g., the fuel interaction with the tank walls) or to include material effects through boundary conditions (e.g., lightning striking a metal substrate). For some material combinations (e.g., lightning striking a metal), it has not even been possible so far to solve for the two phases (plasma arc, elastoplastic solid) simultaneously.

In this work, the methodology for the simultaneous modelling of four states of matter in a single computational code and a single configuration is presented for the first time. It consists of three components: (i) casting the governing equations in a hyperbolic form, (ii) which in turn facilitates the solution of each system using the same, high-resolution, shock-capturing numerical methods, on the same grid and (iii) appropriately solving mixed-material Riemann problems at material interfaces to achieve the communication between materials. Moreover, the innovative combination of diffuse- and sharp-interface methods allowing the non-linear coupling of the four states of matter is also presented here. The simultaneous solution of four states of matter is now possible because of the combination of these three components of our methodology. The innovation relies on all materials being cast in the same mathematical form that allows their solution on the same numerical grid and the new mixed-material Riemann solvers for each pair of materials that allow the appropriate communication between the materials in the framework of a ghost fluid method. It is also aided by the ability to combine sharp and diffuse-interface models as deemed appropriate by the application at hand. At the last part of this work, we demonstrate through a case study the capability of the methodology to solve simultaneously for a plasma arc and elastoplastic solids, in an application involving four states of matter; the lighting strike on a metal container, half-filled with liquid and half-filled with combustible gas.

To describe the elastic behaviour of the solid material in this work, we use the elastic deformation evolution model by Barton et al. [7], further extended later in the work by Schoch et al. [51, 52] and Michael and Nikiforakis [33]. Inelastic deformation follows the approach of Miller and Colella of a predictor–corrector method based on the principle of maximum dissipation and is applied in combination with perfect plasticity and time-dependent plasticity models. Regarding the plasma modelling, resolving the entire resistive MHD system would be inefficient and unnecessary in the context of lightning simulation. Thus, in this work we reduce the MHD equations to mechanical equations which interact with the electrodynamic fields, following [31, 37, 58, 61]. The fluids in this work are described by the compressible form of the Euler equations or multi-phase models suitable for gas, liquid and explosive modelling. Our methodology does not restrict us to a particular formulation for fluid modelling and any formulation in the spectrum of Euler to BN type and hybrid formulations can be used. However, here, we choose to use, based on the application for the case study, the compressible Euler equations for the fluid modelling and augment the plasma model with an equation that allows the multi-phase transition between gas and plasma via the equation of state.

The complete multi-physics system is represented in an Eulerian frame, on a regular Cartesian mesh using Cartesian data structures and all systems of equations are solved with finite volume techniques, employing high-resolution, shock-capturing methods (e.g., MUSCL Hancock with HLLC). The communication between the different systems is achieved by employing the Riemann ghost fluid method and the mixed-material Riemann solvers presented here.

In the remainder of this article, we first present the distinct mathematical formulations describing each of the four states of matter. The technique for communication between the different phases is then presented, including the mixed-material Riemann solvers for plasma-fluid and plasma-solid pairs. The communication between the remaining pairs of states of matter can either be found in [33] or can be trivially extracted from these. Finally, we present the case study, where we investigate the possibility of ignition of a combustible gas lying over a liquid in a metal container that is struck by a plasma arc. We investigate the effect on ignition prevention of the material of the metal container (using aluminium and low-conductivity materials), the effect of the presence of a dielectric coating, sealed and pre-damaged metal containers and insensitive combustible gases.

2 Mathematical Models

In this section, the distinct mathematical formulations describing the four states of matter are presented. The key behind this step is writing all systems of equations in the same, hyperbolic mathematical form, given as

$$\begin{aligned} \frac{\partial {\mathbf {U}} }{\partial t}+ \nabla \cdot \mathbf{F} {\mathbf {(U)}}={\mathbf {S(U)}}. \end{aligned}$$

(1)

2.1 Phases 1 and 2: Modelling the Plasma and the Gas

In this work, we describe the evolution of a plasma arc using the MHD approach of Chemartin et al. [12]. Over the timescales we consider, viscosity effects are negligible and we reduce the system of evolution equations to three conservation laws for the mechanical properties of the plasma; density, $\rho$, momentum, $\rho \mathbf {u}$, and total energy, $\rho E$:

$$\begin{aligned} \frac{\partial \rho }{\partial t}+ \nabla \cdot (\rho {\mathbf {u}})& = 0, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial }{\partial t}(\rho \mathbf {u}_{\mathbf {i}})+\nabla \cdot (\rho \mathbf {u}_{\mathbf {i}}{\mathbf {u}})+\frac{\partial p}{\partial {\mathbf {x}_{\mathbf {i}}}}& = {\mathbf {J}}\times {\mathbf {B}}, \end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial }{\partial t}(\rho E)+\nabla \cdot (\rho E+p){\mathbf {u}}& = {\mathbf {u}} \cdot ({\mathbf {J}} \times {\mathbf {B}})+ \eta {\mathbf {J}} \cdot {\mathbf {J}} + S_{\text {r}}+\rho KQ_{\text {det}}, \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial \rho \lambda }{\partial t}+ \nabla \cdot (\rho {\mathbf {u}}\lambda )& = \rho K, \end{aligned}$$

(5)

$$\begin{aligned} -\nabla ^2{\mathbf {A}}& = \mu _0{\mathbf {J}}, \end{aligned}$$

(6)

$$\begin{aligned} \nabla \cdot {\mathbf {J}}& = -\nabla \cdot (\sigma \nabla \phi )=0, \end{aligned}$$

(7)

where p is the pressure, ${\mathbf {J}}$ the current density, ${\mathbf {B}}$ the magnetic field, which is related to the magnetic vector potential ${\mathbf {A}}$ by ${\mathbf {B}} = \nabla \times {\mathbf {A}}$, $\eta$ the resistivity of the plasma, $S_{\text {r}}$ a term for the radiative losses from a heated material as in [61], $\sigma =1/\eta$ is the electrical conductivity and $\phi$ is the electric potential.

The current density is governed by the boundaries of the domain of interest; for simulations of laboratory arc attachment experiments, there will be an input current and a ground site associated with the circuitry of the experiment.

To model the gaseous explosive, we use the above system of equations, with the hydrodynamic evolution described by (2)–(4) and the combustion process by the equation (5) and the source term $\rho KQ_{\text {det}}$ in (4). In (5), we evolve $\lambda$, the reaction progress variable, taking values between 0 and 1, where 1 indicates that no material has reacted yet and 0 that all material has reacted. The term $\rho KQ_{\text {det}}$ in (4) represents the energy added to the system due to the combustion. The combustion process is assumed to follow a single-step Arrhenius law, such that

$$\begin{aligned} {\frac{{\text {d}}\lambda }{{\text {d}}t}=K=-\lambda C\text{e}^{-\frac{T_{\text {A}}}{T}},} \end{aligned}$$

(8)

where $T_{\text {A}}$ is the gas activation temperature, T the local temperature of the material and C a pre-exponential factor given for the specific material, describing how fast the reaction grows. The heat of detonation is denoted by $Q_{\text {det}}$. Here, $C = 9.1\times 10^{11}{\text{s}}^{-1}, T_{\text{A}} = 8\,000 \, \text{K} \;\text {and}\; Q_{\text {det}} = -4.98\times{10}^{5} \, {\text{J}} \cdot {\text{kg}}^{-1} .$

2.1.1 Current Density Solution

To allow for the full interaction of a plasma arc with a substrate of different conductivities, the full current flow through the substrate has to be computed, as described later in the elastoplastic solids modelling section. By including the interaction of the arc plasma with the substrate, we expect to lose the symmetry in the z-direction of a steady arc. As a result, we expect a radial component to the current density profile (restricting this work to cylindrical symmetry, the azimuthal component remains zero). Effectively, this gives three elliptic equations to solve, the current continuity equation,

$$\begin{aligned} \nabla \cdot (\sigma \nabla \phi )=0 \end{aligned}$$

(9)

and the r- and $\theta$-components of the magnetic potential vector Eq. (6).

When solving these elliptic equations, challenges can arise when there are discontinuous changes in conductivity within the domain; particularly, where the edge of the substrate is adjacent to unionised air, conductivity can drop from $\mathcal {O} (10^7)\,\,\hbox {S} \cdot \hbox {m}^{-1}$ to $\mathcal{O}(10^{-15})\,\,\hbox {S} \cdot \hbox {m}^{-1}$ . These challenges arise due to the fact that derivative quantities (e.g., $\nabla \sigma$ ) are undefined at these discontinuities. Instead of solving the equations in this form, one common technique is to cast them into an integral (weak) form, and apply solution techniques to this form.

To solve the above we use the package DOLFIN, an extension to the FEniCS software [28] and feed the finite element solution (in terms of electric and magnetic potential) to our finite volume numerical method to solve the hyperbolic conservation laws.

2.1.2 Equation of State

The system of Eqs. (2)–(6) comprises 9 equations for 10 unknown variables, $\rho ,E,p, \lambda$ and the vectors ${\mathbf {u}}$ and ${\mathbf {B}}$. These are closed through an equation of state, which describes the thermodynamic properties of the system, typically written in the form $p = p (e, \rho )$, where e is the specific internal energy, and is related to the specific total energy through $\rho E = \rho e + \frac{1}{2} \rho u^2$ (in one dimension). The equation of state of a plasma is complex, since its thermodynamic properties depend strongly on the degree of ionisation.

Over the range of temperatures we consider in this work, from ambient air to a plasma arc centre of over 50 000  K, the ratio of specific heats changes considerably, and hence we cannot use a simple ideal gas-based model. Computing accurate thermodynamic properties then requires detailed knowledge of the composition of a plasma for a given thermodynamic state (e.g., at a given density and internal energy). Here we use a tabulated equation of state based on the 11-species model of Mottura et al. [39], describing the plasma properties over a range of pressures and temperatures. This computes the contribution to energy, sound speed and density from the various species which comprise the plasma. Electrical conductivity is provided as a function of composition following D’Angola et al. [14]. The behaviour of the equation of state as an ideal gas at low temperatures allows the simultaneous modelling of gas and plasma, assuming the gas follows an ideal gas law.

2.1.3 Pre-heated Arc Region

Our current density solution technique incorporates an electrode for current input within the domain; the initial data for this work require a “pre-heated” arc region at the centre of the domain. Physically, the onset of the arc connection is a voltage breakdown of the air between the electrode and the substrate, which generates a conductive path for the current to take. This is a complex process which occurs over timescales much shorter than the plasma arc evolution, and is still not fully understood, and hence cannot be incorporated within our numerical model. The standard technique to provide a conductive path for the current is to assume a thin, high-temperature domain at the centre of the arc [12, 29, 58]. It has been shown by Larsson et al. [29] that this does not affect the overall behaviour of the arc. We use a pre-heated region of ${8\,000}\,\hbox {K}$ with a $2\;\hbox{mm}$ diameter. The current profile used in this work is taken from the literature [2] (Component A therein) and has a rapid rise to a maximum current of ${200}\,\,\hbox {kA}$ over ${6.4}\,\,\upmu \hbox {s}$ and is determined by

$$\begin{aligned} I(t) = I_0(\text{e}^{-\alpha t}-\text{e}^{-\beta t})(1-\text{e}^{-\gamma t})^2, \end{aligned}$$

(10)

where $I_0=218\,810\,\hbox {A}, \alpha = 11\,354\,\,\hbox {s}^{-1}, \beta = 647\,265\,\,\hbox {s}^{-1} \; \text {and} \; \gamma = 5\,423\,540\,\,\hbox {s}^{-1}$.

2.2 Phase 3: Modelling Liquids

To describe the behaviour of a liquid in this context of work, the compressible form of the Euler equations suffices²

$$\begin{aligned} \frac{\partial \rho }{\partial t}+ \nabla \cdot (\rho {\mathbf {u}})& = 0, \end{aligned}$$

(11)

$$\begin{aligned} \frac{\partial }{\partial t}(\rho \mathbf {u}_{i})+\nabla \cdot (\rho \mathbf {u}_{i}{\mathbf {u}})+\frac{\partial p}{\partial {\mathbf {x}_{i}}}& = 0, \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial }{\partial t}(\rho E)+\nabla \cdot (\rho E+p){\mathbf {u}}& = 0, \end{aligned}$$

(13)

where ${\mathbf {u}}=(u,v,w)$ denotes the total vector velocity, i denotes the space dimension, $i=1,2,3$, $\rho$ the total density of the fluid and E the specific total energy given by $E=e+\frac{1}{2}\sum _{i}u_i^2$, with e the total specific internal energy of the system. This form of equations can be used to describe also other fluids, especially ones with complex equations of state.

The particular fluid (gas or liquid) considered is determined by the equation of state that closes the system. For example, air can be modelled by the ideal gas law ($p = \rho (\gamma -1)e$), and water by the stiffened gas equation of state ($p = \rho \left({\gamma - 1}\right)e -\gamma {p_{\infty }}$).

More complex materials, such as reactive components, can be modelled by the MiNi16 model [32] or the MiNi16-reduced formulations and more complex equations of state like the JWL or Cochran–Chan. In the case of explosive modelling, we could use the MiNi16 model or its reduced versions to model the combustion of the material, in which we could have one liquid/solid reactive material turning into gaseous products.

2.3 Phase 4: Modelling Elastoplastic Solids

In this work, we use the elastic solid model described by Barton et al. [7], Schoch et al. [51, 52] and Michael and Nikiforakis [33], based on the formulation by Godunov and Romenskii [22]. The plasticity is included following the work of Miller and Colella [36].

If we consider an elastoplastic material in isolation in an Eulerian frame, which we employ here, there is no mesh distortion that can be used to describe the solid material deformation. The material distortion, therefore, needs to be accounted for in a different way. Here, this is done by defining the total deformation gradient tensor as

$$\begin{aligned} F_{ij} = \frac{\partial x_i}{\partial X_j}, \end{aligned}$$

(14)

which maps the initial configuration (coordinate ${\mathbf {X}}$) to the deformed configuration (coordinate ${\mathbf {x}}$). Following the proposition by Rice [47] we introduce an intermediate configuration describing only plastic deformations described by ${\mathbf {F}}^p$ such that the total deformation is decomposed multiplicatively into elastic and plastic components as ${\mathbf {F}}={\mathbf {F}}^e{\mathbf {F}}^p$.

The state of the solid is characterised by the elastic deformation gradient, velocity $u_i$ and entropy S. Following the work by Barton et al. [7], the complete three-dimensional system forms a hyperbolic system of conservation laws (15)–(18) for momentum, strain and energy:

$$\begin{aligned} \frac{\partial {\rho u_i}}{\partial t} + \frac{\partial (\rho u_i u_m - \sigma _{im})}{\partial x_m}& = 0, \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial {\rho E}}{\partial t} + \frac{\partial (\rho u_m E - u_i \sigma _{im})}{\partial x_m}& = \eta J_i J_i, \end{aligned}$$

(16)

$$\begin{aligned} \frac{\partial {\rho F^e_{ij}}}{\partial t} + \frac{\partial (\rho F^e_{ij}u_m-\rho F^e_{m j}u_i)}{\partial x_m}& = -u_i\frac{\partial \rho F^{e}_{mj}}{\partial x_m} + P_{ij}, \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial {\rho \kappa }}{\partial t} + \frac{\partial (\rho u_m \kappa )}{\partial x_m}& = \rho \dot{\kappa }, \end{aligned}$$

(18)

$$\begin{aligned} -\nabla ^2A_i& = \mu _0 J_i, \end{aligned}$$

(19)

with the vector components $\cdot _i$ and tensor components $\cdot _{ij}$. The first two equations along with the density-deformation gradient relation

$$\begin{aligned} \rho = \rho _0 / \text {det}\;{\mathbf {F}}^e, \end{aligned}$$

(20)

where $\rho _0$ is the density of the initial unstressed medium, essentially evolve the solid material hydrodynamically. Here, $\sigma$ is the stress, E the specific total energy such that $E=\frac{1}{2}|\mathbf{u}|^2+e$, with e the specific internal energy and $\kappa$ the scalar material history that tracks the work hardening of the material through plastic deformation. We denote the source terms associated with the plastic update as $P_{ij}$.

Electrodynamic effects are present within the solid material, though only through the Joule effect in the energy equation ($\eta J_i J_i$). The Lorentz effect does not apply to solid materials, where intermolecular forces prevent material flow with the magnetic field. We, therefore, solve for the magnetic vector potential and current density as we do for a plasma through Eqs. (6) and (7).

The system is closed by an analytic constitutive model relating the specific internal energy to the deformation gradient, entropy and material history parameter (if applicable):

$$\begin{aligned} e = e({\mathbf {F}}^e,S,\kappa ). \end{aligned}$$

(21)

We restrict this work to isotropic materials, $e({\mathbf {F}}^e)=e(I_1,I_2,I_3, S)$, with $I_1,I_2,I_3$ the invariants of the Finger tensor given by $\varvec{C} = \varvec{F}^{-T}\varvec{F}^{-1}$. The stress tensor is given by

$$\begin{aligned} \sigma _{ij} = \rho F^e_{im}\frac{\partial e}{\partial F^e_{jm}} \end{aligned}$$

(22)

or equivalently,

$$\begin{aligned} \varvec{\sigma } = -2\rho \left[ \frac{\partial e}{\partial I_3}I_3\,\mathcal {I} + \left( \frac{\partial e}{\partial I_1} + I_1 \frac{\partial e}{\partial I_2}\right) \varvec{C} - \frac{\partial e}{\partial I_2} \varvec{C}^2\right] . \end{aligned}$$

(23)

For ${\mathbf {F}}$ to represent physical, continuous deformations, it must satisfy three compatibility constraints:

$$\begin{aligned} \frac{\partial \rho F_{kj}}{\partial x_k} = 0, \quad j=1,2,3, \end{aligned}$$

(24)

which hold true for $t>0$ if true for initial data.

The deformation is purely elastic until the stress state is evolved beyond the yield surface ($f>0$), which in this work is given by the Von Mises criterion

$$\begin{aligned} f(\varvec{\sigma } )=||\text {dev}\varvec{\sigma }||-\sqrt{\frac{2}{3}}\sigma _Y = 0 \; \text {with} \;\; \text {dev} \varvec{\sigma } = \varvec{\sigma }-\frac{1}{3}(\text {tr}\varvec{\sigma })I, \end{aligned}$$

(25)

where $\sigma _Y$ is the yield stress and the matrix norm ||·|| the Shur norm ($||\varvec{\sigma }||^2=\text {tr}(\varvec{\sigma }^{\text {T}}\varvec{\sigma }$)).

As this identifies the maximum yield allowed to be reached by an elastic-only step, a predictor–corrector method is followed to re-map the solid state onto the yield surface. Assuming that the simulation timestep is small, this is taken to be a straight line, using the associative flow rate ($\dot e^p=\chi \frac{\partial F}{\partial \sigma }$), satisfying the maximum plastic dissipation principle (i.e., the steepest path). In general, this re-mapping procedure is governed by the dissipation law

$$\begin{aligned} \psi _{\text {plast}} =\varvec{\varSigma } :(({\mathbf {F}}^p)^{-1}\dot{{\mathbf {F}}^p}), \end{aligned}$$

(26)

where $\varvec{\varSigma }=\varvec{G}\varvec{\sigma }\varvec{F}$ and $:$ is the double contraction of tensors (e.g., $\varvec{\sigma }:\varvec{\sigma }=\text {tr}(\varvec{\sigma }^{\text {T}}\varvec{\sigma })$). The initial prediction is ${\mathbf {F}} = {\mathbf {F}}^e$ and ${\mathbf {F}}^p = {\mathbf {I}}$, where ${\mathbf {F}}$ is the specific total deformation tensor and ${\mathbf {F}}^p$ the plastic deformation tensor that contains the contribution from plastic deformation. This is then relaxed to the yield surface according to the procedure of Miller and Colella [36].

For the aluminium used in this work, we use the Romenskii hyperelastic equation of state [59], consisting of a two-term hydrodynamic component and a one-term shear deformation component. The full equation is given by

$$\begin{aligned} e (I_1,I_2,I_3,S) = \frac{K_0}{2\alpha ^2}\left( I_3^{\alpha /2}-1\right) ^2+ c_v T_0 I_3^{\gamma /2}\left( \text{exp}{\left(S/c_v\right)}-1\right) +\frac{B_0}{2}I_3^{\beta /2}\left( \frac{I_1^2}{3}-I_2\right) , \end{aligned}$$

(27)

where $I_1,I_2,I_3$ are the invariants of the Finger tensor, $K_0=c_0^2 - \frac{4}{3}b_0^2$ is the squared bulk speed of sound, $b_0$ (with $B_0 = b^{2}_{0}$) is the reference shear wave speed, $c_v$ is the specific heat capacity at constant volume, $T_0$ is the reference temperature, $\alpha$ and $\gamma$ are exponents determining the non-linear dependence of the sound speed and temperature on density, respectively, and $\beta$ an exponent determining the non-linear dependence of this shear wave speed on density.

The constitutive model parameters for the aluminium considered here are given in Table 1. Perfect plasticity is assumed, with a yield stress of ${0.4}\,\hbox {GPa}$. The conductivity of the aluminium is taken to be $3.2\times 10^7\,\hbox {S} \cdot \hbox {m}^{-1}$.

Table 1 Romenskii equation of state parameters the elastoplastic solid materials used in this work

For the PMMA dielectric considered in this work we use a shock Mie-Grüneisen equation of state:

$$\begin{aligned} p = \frac{\rho _0c_0^2}{s(1-s{\eta_{\textsc{mg}} })}\Bigg (\frac{1}{1-s{\eta_{\textsc{mg}}} }-1\Bigg ), \end{aligned}$$

(28)

where ${\eta_{\textsc{mg}}} =1-\frac{\rho _0}{\rho }$, $c_0$ is the material sound speed, $\rho _0$ is the reference density and s a single experimentally determined coefficient. For PMMA, these parameters take the values:

$$\begin{aligned} \rho _0 = 1\,180\,\,\hbox {kg}\cdot \hbox {m}^{-3}, \qquad c_0 = 2\,260\,\,\hbox {m} \cdot \hbox {s}^{-1} \qquad \text {and} \qquad s=1.82. \end{aligned}$$

(29)

The PMMA dielectric is considered to have conductivity of 2.6 × 10⁻⁵ S·m⁻¹. The low-conductivity material we consider in this work which can be considered an isotropic approximation to carbon fibre reinforced plastic, follows the same equation of state as the aluminium, with a lower conductivity value of $41\,260\,\,\hbox {S} \cdot \hbox {m}^{-1}$.

2.4 Solving for Each Phase

As all the systems of equations are in a hyperbolic form, we can use finite volume methods to solve for each phase (here Slope Limited Centred). This will give solutions at all pure-material cells. Validation for the individual components can be found in previous work [33, 37, 60]. The next step, described in the section that follows, is how to apply material boundary conditions and fill in the cells adjacent to the material boundary, for which we need information from both materials.

3 The Multi-material Approach

In this work, we use level set methods to track the material interfaces given by the boundaries of the three partial differential equations (PDE) systems (referred to as materials in this framework) described in the previous section. Note that in this work there is not a sharp interface between plasma and unionised gas, as the two materials are modelled using the same equation of state. The change in state of matter happens gradually over a diffuse region, with the degree of ionisation being a function of temperature and pressure.

Level set methods only give the location of an interface; they do not affect the evolution of the material components. The behaviour of the material components at the interface is modelled by the implementation of dynamic boundary conditions using the Riemann ghost fluid method with appropriately constructed mixed-material Riemann solvers to solve the interfacial Riemann problems between materials. We use the Riemann ghost fluid method instead of the original ghost fluid method [18] because it handles discontinuities between different materials without introducing oscillations at the interface.

Level set methods determine the location of an interface through the zero contour of a signed distance function, $\phi_{\textsc{ls}} (x,y)$, typically referred to as the level set function, given by $\varPhi = {(x,y)|\phi_{\textsc{ls}} (x,y)=0}$. The level set function is an implicit representation of the interface and we store only discretised values of the function, $\phi _{{\textsc{ls}}i} =\phi _{\textsc{ls}}(\mathbf{x}_{i})$. The sign of the function can determine where a material is present within the computational domain. For simulations with three or more materials, each material has its own level set function, and is present in the region $\phi _{\textsc{ls}i}^m > 0$, where m is the material index. The evolution of $\phi_{\textsc{ls}} (x,y)$, assuming no mass transfer across the interface, is given by the advection equation

$$\begin{aligned} \frac{\partial \phi_{\textsc{ls}} }{\partial t} + {\mathbf {u}} \cdot \nabla \phi_{\textsc{ls}} =0, \end{aligned}$$

(30)

where $\mathbf{u}$ is the velocity corresponding to the material for which the level-set function in cell i has a positive value.

Due to numerical error it is possible that, within any particular cell, there may not be a unique material with positive level-set value. We use the projection method of Losasso et al. [30] to correct the level set values should this arise.

The Riemann ghost fluid method of Sambasivan and Udaykumar [48, 49] is used to model the behaviour of the material component at the interface. This method, in contrast to the original ghost fluid method [18], uses the solution to a mixed-material problem to compute the dynamic boundary conditions at ghost cell states adjacent to the interface. For every cell i adjacent to the interface the following procedure is used:

• i. locate the interface within the cell at the point $P=i+\phi_{\textsc{ls}} \nabla \phi_{\textsc{ls}};$

• ii. project two probes into the adjacent materials, reaching the points $P_1=P+{\mathbf {n}} \cdot \varDelta x$ and $P_2=P-{\mathbf {n}} \cdot \varDelta x;$

• iii. interpolate states at each point using information from the surrounding cells;

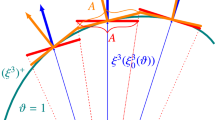
• iv. solve a mixed-material Riemann problem (as described in Sect. 3.1) between the two states to extract the state of the real-material cells, adjacent to the interface (left star state $\mathbf {W^*_{\text {L}}}$, in Fig. 1);

• v. replace the state in cell i by the computed star state.

After the above procedure is followed for each material, a fast-marching method is used to fill in the ghost cells for each material.

3.1 Mixed-material Riemann Solvers

In this section we describe how the mixed-material Riemann problems at material interfaces are solved (step iv in the procedure described above). A separate mixed-material Riemann problem needs to be constructed for each pair of governing equations. We present mixed-material Riemann problem solutions for two key material pairs. The remaining solvers follow these methods closely, and can be found in previous work. The Riemann solver at the material interface takes two states from the two different materials as input; these states can be modelled by different mathematical models. The solution to a given problem provides a one-sided solution to the interface-adjacent (star) state. This solution is based on the characteristic equations computed from the mathematical system describing one of the materials and by invoking appropriate “boundary conditions” between the two materials at the interface. Without loss of generality, we consider the characteristic equations to describe the material to the left of the interface. In this section, we first describe how the plasma-gas model is coupled with the liquid model (i.e., a simple Euler system) and then with a full elastoplastic solid system. The remainder combinations should be directly deducible from these or found in [33].

3.1.1 Plasma-Gas Coupled with Liquid

We consider a material interface, on the left side of which is a plasma governed by the equations of Sect. 2.1 with our tabular equation of state, and on the right side is a liquid material governed by the Euler equations with an equation of state in the form of ideal gas or a more complex equation of state (e.g., stiffened gas, JWL). Henceforth we assume that we are currently solving for the plasma material (in ghost fluid method terminology, the “real” material). At the material boundary a Riemann problem is solved between the left plasma and the right liquid Euler system to provide the star state for the real material. We use a Riemann solver that takes into account the two different materials and all the wave patterns in the Euler system, as described in this section.

We write the hyperbolic part of the plasma model in primitive form as ${\mathbf {W}}_t+\mathbf {A(W)W}_x=\mathbf {0}$, with

$$\begin{aligned} {\mathbf {W}} = \left[ \begin{array}{c} \rho \\ u \\ w \\ p \\ \lambda \end{array} \right] , \quad {\mathbf {A}}({\mathbf {W}}) = \left( \begin{array}{ccccccc} u &{} \rho &{} 0 &{} 0 &{} 0\\ 0 &{} u &{} 0 &{} 1/\rho &{} 0 \\ 0 &{} 0 &{} u &{} 0 &{} 0 \\ 0 &{} \rho c^2 &{} 0 &{} u &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} u \\ \end{array} \right) . \end{aligned}$$

(31)

The Jacobian matrix ${\mathbf {A}}({\mathbf {W}})$ has eigenvalues $\mu _1 =\mu _2=\mu _5=u$, $\mu _3=u-c$ and $\mu _4=u+c$, where c is the sound speed of the material.

The right eigenvectors are

$$\left\{ \begin{aligned} {\mathbf {r}}_1& = \left( 1 ,0 , 0 , 0, 0 \right) ^{\text {T}}, \quad {\mathbf {r}}_2 = \left( 0 ,0 , 1 , 0, 0 \right) ^{\text {T}},\nonumber \\ {\mathbf {r}}_3& = \left( 1 , -c, 0, \rho c^2, 0 \right) ^{\text {T}},\quad {\mathbf {r}}_4 = \left( 1 , c, 0, \rho c^2, 0 \right) ^{\text {T}}, \quad {\mathbf {r}}_5 = \left( 0 ,0 , 0 , 0,1 \right) ^{\text {T}} \end{aligned}\right. $$

(32)

and the left eigenvectors are

$$\left\{\begin{aligned} {\mathbf {l}}_1& = \left( -c^2 ,0 , 0 , 1, 0 \right) ,\quad {\mathbf {l}}_2 = \left( 0 , 0 , 1 , 0, 0 \right) ,\nonumber \\ {\mathbf {l}}_3& = \left( 0 , -\rho c , 0 , 1, 0 \right) ,\quad {\mathbf {l}}_4= \left( 0 ,\rho c , 0 , 1, 0 \right) ,\quad {\mathbf {l}}_5= \left( 0 ,0,0 , 0 , 1 \right) . \end{aligned}\right.$$

(33)

Fig. 1

Riemann problem at the material interface between a plasma and a fluid (e.g., liquid) or solid elastoplastic material. The shaded region represents the initial ghost region and the white region the initial “real” material region in GFM terminology. We are solving for the material in the white, left region. For plasma, the one-sided solution comprises two or more degenerate and hence overlapping waves

Characteristics define directions $\frac{{\text {d}}x}{{\text {d}}t}=\mu _j$, in which

$$\begin{aligned} {\mathbf {l}}^{(i)} \cdot {\text {d}}{\mathbf {W}} = 0, \quad \text {where} \quad {\text {d}}{\mathbf {W}}= \left( {\text {d}}\rho , {\text {d}}u , {\text {d}}w , {\text {d}}p, {\text {d}}\lambda \right) ^{\text {T}}. \end{aligned}$$

(34)

Therefore, along $\frac{{\text {d}}x}{{\text {d}}t}=\mu _j=u$ for $j=1,2$ and 5 we obtain, respectively

$$\begin{aligned} {\text {d}}p-c^2 {\text {d}}\rho& = 0, \end{aligned}$$

(35)

$$\begin{aligned} {\text {d}}w& = 0, \end{aligned}$$

(36)

$$\begin{aligned} {\text {d}}\lambda& = 0. \end{aligned}$$

(37)

And along $\frac{{\text {d}}x}{{\text {d}}t}=\mu _3=u-c$ and $\frac{{\text {d}}x}{{\text {d}}t}=\mu _4=u+c$, we obtain

$$\begin{aligned} {\text {d}}p-\rho c\, {\text {d}}u& = 0, \end{aligned}$$

(38)

$$\begin{aligned} {\text {d}}p+\rho c\,{\text {d}}u& = 0. \end{aligned}$$

(39)

For a single phase described by the ideal gas or stiffened gas equation of state, the characteristic equations can be integrated directly, as the expressions for the sound speed are simple. However, for more complex or tabular equations this might not be possible. In such case, one can obtain an approximate mixed-material Riemann solver by replacing the differentials with the difference of the initial and the final state without integrating (i.e., across the characteristics), as presented below.

Using ${\text {d}}p + \rho c\, {\text {d}}u=0$, we connect the states ${\mathbf {W}}^*_{\text {L}}$ and ${\mathbf {W}}_{\text {L}}$ to obtain

$$\begin{aligned} p^*_{\text {L}}-p_{\text {L}} = - \rho _{\text {L}} c_{\text {L}}(u^*_{\text {L}} - u_{\text {L}}). \end{aligned}$$

(40)

Using ${\text {d}}p - \rho c\, {\text {d}}u=0$, we connect the states ${\mathbf {W}}^*_{\text {R}}$ and ${\mathbf {W}}_{\text {R}}$ to obtain

$$\begin{aligned} p^*_{\text {R}}-p_{\text {R}} = \rho _{\text {R}} c_{\text {R}}(u^*_{\text {R}} - u_{\text {R}}). \end{aligned}$$

(41)

Pressure and velocity do not change across the material interface, hence $p^*_{\text {L}}=p^*_{\text {R}}=p^*$ and $u^*_{\text {L}}=u^*_{\text {R}}=u^*$. Applying these conditions to (40) and (41) we obtain expressions for $p^*$ and $u^*$:

$$\begin{aligned} p^* = p_{\text {L}} - \rho _{\text {L}} c_{\text {L}}(u^*-u_{\text {L}}) \quad \text {and} \quad u^* = \frac{p^*-p_{\text {R}}}{\rho _{\text {R}}c_{\text {R}}} + u_{\text {R}}. \end{aligned}$$

(42)

Solving the above two simultaneously, we obtain an expression for the pressure in the star region:

$$\begin{aligned} p^* = \frac{C_{\text {R}} p_{\text {L}} - C_{\text {L}} p_{\text {R}}-C_{\text {R}}C_{\text {L}}(u_{\text {R}}-u_{\text {L}})}{C_{\text {R}}+C_{\text {L}}}, \end{aligned}$$

(43)

where $C_{\text {L}} = \rho _{\text {L}}c_{\text {L}}$ and $C_{\text {R}}=\rho _{\text {R}}c_{\text {R}}$.

To calculate the left fluid (here gaseous) state, we connect states ${\mathbf {W}}^*_{\text {L}}$ and ${\mathbf {W}}_{\text {L}}$, using Eq. (40) and ${\text {d}}p-c^2{\text {d}}\rho =0$ to obtain

$$\begin{aligned} u^*& = \frac{p_{\text {L}}-p^*}{\rho _{\text {L}}c_{\text {L}}} + u_{\text {L}}, \quad \end{aligned}$$

(44)

$$\begin{aligned} \rho ^*_{\text {L}}& = \frac{p^*-p_{\text {L}}}{c_{\text {L}}^2} + \rho _{\text {L}}. \end{aligned}$$

(45)

Using the remaining characteristic equations we obtain

$$\begin{aligned} w^*=w_{\text {L}} \quad \text {and} \quad \lambda ^*=\lambda _{\text {L}} \end{aligned}.$$

(46)

Equations (43)–(46) give the full state in the left star region. The values of $C_{\text {L}},C_{\text {R}}$ and $c^2_{\text {L}}$ in Eqs. (43)–(45) are constant approximations of the $(\;)_{\text {L}}$ and $(\;)_{\text {R}}$ values, although other approximations can be taken.

3.1.2 Plasma-Gas Coupled with Solid

We now consider an interface on the left of which is again a plasma, governed by the equations of Sect. 2.1 with our tabular equation of state (plasma-gas material) and on the right side is a material governed by the elastoplastic solid equations (the solid material) of Sect. 2.3. We develop a Riemann solver that takes into account the two different materials to determine the star state in the plasma-gas material.

We follow a similar procedure to that in Sect. 3.1.1. Referring to Fig. 1, ${\mathbf {W}}_{\text {L}}$ corresponds to the original plasma state, ${\mathbf {W}}_{\text {R}}$ to the original elastoplastic state and ${\mathbf {W}}^*_{\text {L}}$ to the plasma star state that we are looking to compute with this Riemann solver. Since we are solving for the plasma as the real material, the Riemann problem still has three types of waves (two non-linear and two overlapping linear in 1D). The same characteristic relations (35)–(39) are defined as before and we use the approach of representing the differentials with the state difference. Connecting fluid states ${\mathbf {W}}^*_{\text {L}}$ and ${\mathbf {W}}_{\text {L}}$ using ${\text {d}}p + \rho c\, {\text {d}}u=0$ and solid states ${\mathbf {W}}^*_{\text {R}}$ and ${\mathbf {W}}_{\text {R}}$ using ${\text {d}}p - \rho c\, {\text {d}}u=0$ we obtain a mixed-material expression for $p^*$:

$$\begin{aligned} p^*=\frac{{u_S-u_F + \frac{1}{\rho _S}({\mathbf {Q}}^{-1}\mathcal {D}^{-1}{\mathbf {Q}})^S_{11}\sigma ^S_{11}+\frac{p_F}{\rho _Fc_F}}}{\frac{1}{\rho _Fc_F}-\frac{1}{\rho _S}({\mathbf {Q}}^{-1}\mathcal {D}^{-1}{\mathbf {Q}}\ )^S_{11}\sigma ^S_{11}}, \end{aligned}$$

(47)

where ${\mathbf {Q}}$ is an orthogonal matrix and $\mathcal {D}$ is the diagonal matrix of positive eigenvalues for the solid system, such that the elastic acoustic tensor is defined by

$$\begin{aligned} \varOmega _{ij}=\frac{1}{\rho }\frac{\partial \sigma _{1i}}{\partial F^e_{jk}}{\mathbf {F^e}}_{1k}={\mathbf {Q}}^{-1}\mathcal {D}^{-1}{\mathbf {Q}}. \end{aligned}$$

(48)

Considering $p_{\text {R}}=\sigma ^S_{11},({\mathbf {Q}}^{-1}\mathcal {D}^{-1}{\mathbf {Q}})^S_{11}=1/c_{\text {R}}$ and $C_{\text {R}} = \rho _{\text {R}}c_{\text {R}}$ and $C_{\text {L}}=\rho _{\text {L}}c_{\text {L}}$ we obtain Eq. (43).

Then, using $\text{d}p+c^2\text{d}\rho =0$ to connect states ${\mathbf {W}}^*_{\text {L}}$ and ${\mathbf {W}}_{\text {L}}$ we obtain Eqs. (44)–(45) and values for $u^*_{\text {L}}$ and $\rho ^*_{\text {L}}$, using the remaining characteristic equations we obtain equations (46) and values for $w^*$ and $\lambda ^*$. At the interface, we apply conditions

$$\begin{aligned} p^*_{\text {L}} = \sigma ^*_{\text{R},11}, \quad u^*_{\text {L}}=u^*_{\text {R}}. \end{aligned}$$

(49)

To improve accuracy and robustness, an iterative approach as described in [33] can be used. The coupling of the remainder material combinations follow from the above. Validation for each mixed-material Riemann solver can be found in previous work [33, 60].

4 Lightning Strike on Elastoplastic Substrates

In this section we exercise our multi-physics methodology applied to the simultaneous solution of four states of matter to study lightning-strike scenarios that could lead to the ignition of a combustible gas, in a metal container containing liquid and gaseous phases. We consider a closed container made of aluminium, or a similar metal with lower electrical conductivity, and the cases in which the container is coated with an upper dielectric paint layer. We can consider either this dielectric layer or the entire top of the container (dielectric and metal) to be pre-damaged (opened). In the metal container we consider a liquid material upon which is an upper region of a combustible gas. All simulations are performed in cylindrical symmetry, with the z-axis the axis of symmetry.

4.1 Sealed Aluminium Substrate

In this section we consider the simulation of plasma arc attachment to an undamaged aluminium substrate, underneath which a layer of a combustible gas and a layer of liquid are placed. As there is no gap or hole on the aluminium, the plasma arc can only interact indirectly with the combustible gas; any effects have to propagate through the aluminium substrate. Beneath the two fluids lies another layer of the same aluminium, forming a closed metal container, as the aluminium, both on top and bottom is extended to the right end of the domain. A schematic of the initial configuration in 2D is shown in Fig. 2a.

Fig. 2

Setup of the simulations without (left) and with (right) a vented dielectric. All distances are in meters

For the gas within the container to start reacting, the temperature needs to rise sufficiently to activate the temperature-dependent Arrhenius term in (8). In this case, even though the gas is sensitive ($T_{\text {A}}={8\;000}\,\hbox {K}$), the initiation of reaction requires temperatures of the order of $1\;000\,\,\hbox {K}$. Over the duration of this simulation, the temperature increases only a few degrees, up to ${270}\,\hbox {K}$, as shown in Fig. 3a (purple). The temperature rise in this simulation comes from the equation of state responding to the pressure rise of the material, hence the two quantities follow the same trend. The pressure rise in the combustible gas is due to a pressure wave propagated from the plasma arc through the aluminium substrate and then to the gas. In Fig. 4, we study the pressure waves generated in the early stages of the simulation. The rapid growth of the plasma arc induces a pressure wave in the aluminium of the order of ${2.6}\,\hbox {MPa}$. The current input into the system reaches its peak at ${6}\,\upmu \hbox {s}$, at which point we see maximum pressures of the order of ${85}\,\hbox {MPa}$ in the aluminium. The induced pressure in the combustible gas is considerably lower than that (${0.1}\,\hbox {MPa}$), as demonstrated by the pressure contours and pressure field in Fig. 4. This is due to the initial shock wave travelling through the aluminium reflecting off of the bottom of the layer, generating a strong rarefaction which serves to mitigate the pressure increases in the combustible gas. The increase of the pressure over the duration of the simulation is shown in Fig. 3b (purple). Since the maximum current input occurs at ${6}\,\upmu \hbox {s}$ and thereafter the current profile follows an exponential decay, we do not expect the pressure and temperature rise to ignite the material in this scenario. Indeed the $\lambda$-field remains at the value 1 (i.e., reactants have not been depleted) throughout the simulation, demonstrating that ignition does not occur in this configuration, over these timescales. The high electrical conductivity of aluminium serves to mitigate temperature rise within the substrate, and therefore, even over longer timescales, there will not be sufficient temperature diffusion to ignite the combustible gas.

Fig. 3

Maximum temperature (left) and pressure (right) in the combustible gas throughout the simulation, for an uncoated aluminium substrate (purple) and PMMA-coated aluminium substrate, with a gap on the PMMA dielectric (green)

Fig. 4

Pressure distribution (in Pa) in plasma, aluminium and combustible gas for the uncoated, sealed aluminium case. The material boundary of the aluminium substrate is indicated by the white line, while the interface between the combustible gas and the liquid (whose pressure is not shown here) is indicated by the blue line

4.1.1 Sealed Aluminium Substrate, Coated with Opened Dielectric Layer

We place a dielectric layer, with a thickness of $10\,\,\hbox {mm}$ and a $2\,\,\hbox {mm}$-radius gap at the centre over the aluminium substrate, representative of the situation in which there is existing damage to the coated layer (e.g., due to the electric breakdown which generates the arc), but not to the metal substrate, as shown in Fig. 2b. We use this test to study the pressure and temperature rise in the combustible gas as before, to asses the possibility of ignition in this configuration over short timescales. The channel produced by the opening of the dielectric layer can lead to a funneling effect for the plasma which can increase the pressure locally, and this is known to increase local damage to the metal substrate. Therefore, we investigate if this effect is enough to raise the temperatures and pressures in the combustible material and lead to the ignition of the combustible material. As in the uncoated aluminium case, in the duration of this simulation the temperature increases only a few degrees, up to $270\,\hbox {K}$, as shown in Fig. 3a (green). Again, the temperature rise in this simulation comes from the equation of state responding to the pressure rise of the material. The pressure rise in the combustible gas is due to a pressure wave propagated from the arc to the aluminium substrate and then to the gas. However, the presence of the dielectric restricts the attachment area of the arc, since little current can pass through the dielectric layer, and this serves to focus the Joule heating effect within the aluminium. In Fig. 5 we study the pressure waves generated in the early stages of the simulation. The growth of the plasma arc induces a pressure wave in the aluminium of the order of ${2.6}\,\hbox {MPa}$. The maximum pressure in the aluminium in this case is lower than in the aluminium-only case, reaching values of the order of ${80}\,\hbox {MPa}$. This lower pressure is a result of the mechanical interaction between the plasma arc and the dielectric layer. This layer prevents the surface of the aluminium from being in contact with the leading shock wave of the arc, thus reducing the pressure loading. However, the concentrated current density during attachment will lead locally to higher energy in the case of a coated aluminium substrate. The induced pressure in the combustible gas is again considerably lower than that (${0.1}\,\hbox {MPa}$), as demonstrated by the pressure contours and pressure field in Fig. 5. The maximum pressure in the duration of the simulation is shown in Fig. 3b. As the maximum current occurs at ${6}\,\upmu \hbox {s}$ and thereafter the current profile demonstrates an exponential decay, we do not expect the pressure and temperature rise to ignite the material in this scenario. Again, the $\lambda$-field remains at the value 1 throughout the simulation, demonstrating that ignition does not occur in this configuration, over these timescales.

Fig. 5

Pressure distribution (in Pa) in plasma, aluminium and combustible gas. The material boundary of the aluminium substrate is indicated by the white line, while the interface between the combustible gas and the liquid (whose pressure is not shown here) is indicated by the blue line and the material boundary of the dielectric is indicated by the fuchsia line

4.2 Opened Aluminium Substrate

In this section we consider the simulation of an arc attachment to an aluminium substrate that is assumed to have already been punctured, beneath which a layer of a combustible gas and a layer of liquid are present. Since a gap is considered to already exist, either due to an improper lightning protection scheme allowing damage from a previous lightning strike, or by other means, the arc interacts directly with the combustible gas. The lower edge of the container is assumed not to be damaged, and the aluminium, both on top and bottom is extended to the right end of the domain. A schematic of the initial configuration in 2D is shown in Fig. 6a.

Fig. 6

Setup of the simulations without (left) and with (right) a dielectric coating. All distances are in meters

Figure 7 shows the evolution of pressure fields in the four materials. It should be noted that the plasma arc initially attaches to the open-end of the aluminium, as shown in Fig. 9a. Figure 7a shows the initial conditions for the simulation and in Fig. 7b a pressure loading is evident on the aluminium substrate; a shock wave is seen to propagate in the aluminium. The shock wave progressing through the combustible gas is also shown, which raises the pressure by two orders of magnitude (Fig. 7b). The shock wave in the combustible gas reaches the liquid boundary, and as it travels from a low impedance to a high impedance medium, it generates a further shock wave in the liquid and another reflects into the combustible gas (Fig. 7c). As this wave propagates upwards through the combustible gas, it reaches the top of the container, where it interacts with the aluminium, producing another shock wave in the aluminium and generating a rarefaction wave from the corners of the hole in the aluminium back into the gas (Fig. 7d). When the shock wave in the liquid reaches the bottom of the aluminium container, it also generates a shock in the aluminium and a rarefaction back into the liquid (Fig. 7e). The complex wave and material interactions continue to late stages (Fig. 7f).

As the arc evolves over time, the highest pressure remains at the centre, due to the Joule heating effects, with the majority of the pressure loading on the combustible gas occurring here. A corresponding wave moves through the substrate as the shock wave imparts a loading effect, though this is substantially lower than at the centre of the arc. We note that while the pressure within the plasma arc must strictly stay positive, within the substrate, negative values are experienced. This is because pressure is a component of the stress tensor, and a solid material can sustain tension, as a result of rarefaction waves.

Fig. 7

Pressure distribution (in Pa) in the plasma, combustible gas, aluminium substrate and liquid, at different times, for the uncoated, opened aluminium case

As we are interested in the ignition of the combustible gas, which is a temperature-driven effect, we present the temperature profiles (right half) and reaction progress (left half) in Fig. 8, while again showing the pressure profile in the plasma arc, the liquid and the aluminium. Along with the distribution of temperature in the combustible gas, we present the temperature contour of $1\;000\,\,\hbox {K}$, as the reaction starts at this lower temperature and grows rapidly as the temperature increases further. The initial pressure loading is enough to immediately ignite the material, reaching temperatures of $8\;000\,\,\hbox {K}$. As the combustible gas is sensitive, this initial pressure loading leads to its direct combustion. Therefore, the high-temperature regions on the right of the figures (e.g., Fig. 8b) are accompanied by a region of burnt material shown in the reaction progress variable on the left of the figure. The shape of the reaction region follows the curved path of the pressure wave and induced temperature field due to the interaction of this wave around the corner of the gap in the aluminium. As the reaction front reaches the liquid interface, it is forced to propagate laterally, thus giving the curved reaction front, as shown in Fig. 8d.

The rarefaction waves generated at the gas/solid interface work to lower the pressure and temperature and weaken the reaction, while the shocks at the liquid/gas interface work to elevate the pressure and temperature and strengthen the reaction. Moreover, the dynamic profile of the current density also works to elevate the pressures and temperatures at the left (back) end of the reaction, continuously altering the rear boundary condition of the region. The reaction continues (Fig. 8f) throughout this complex wave interaction until the combustible gas is depleted.

Fig. 8

Pressure distribution (in Pa) in the plasma, aluminium substrate and liquid, at different times, for the uncoated, opened aluminium case. In the combustible gas, the temperature field (in K) is shown on the right half and the $\lambda$-field on the left half of each plot. On the right half, the contour of temperature of 1 000 $\hbox {K}$ is also shown

4.3 Opened, Low-Conductivity Substrate

Lightning strikes input a large amount of energy into the substrate through the Joule heating effect, the spatial extents over which this occurs is governed by the electrical conductivity of the material. High-conductivity materials like aluminium spread this energy over the entire strike path through the substrate, and thus minimise damage, but the lower conductivity of composite materials, such as carbon fibre reinforced plastics (CFRP), means much more energy is deposited local to the impact site. Coupled with the lower thermal conductivity of these materials, this leads to substantial heating over diffusion timescales, and hence lightning strike has the potential to be much more damaging. As a result, we want to investigate the effect of replacing aluminium with CFRP on the ignition and detonation of the combustible gas lying beneath the elastoplastic substrate. To fully model a CFRP substrate, we need an anisotropic equation of state which models the orientations of the fibre weave comprising the substrate. To model the effects within cylindrical symmetry, we consider an isotropic approximation to CFRP, in which we consider an electrical conductivity corresponding to the direction along the fibre weave of $41\,260\,\hbox {S} \cdot \hbox {m}^{-1}$. This is substantially lower than the conductivity of the aluminium ($3.2 \times 10^{7}\,\hbox {S} \cdot \hbox {m}^{-1}$).

Figure 9 shows differences in the arc structure, with much greater spreading at the arc root on the composite panel. The lower electrical conductivity of the substrate is comparable to that of high-temperature plasma, thus the optimal current path is to travel further through the plasma, reducing the overall distance to the ground site. Investigation of the resulting reaction progress variable contours in the detonation showed no difference between the two substrates hence we conclude that there is no impact on detonation by the change of the substrate material. This follows from the altered path of the current profile, the initial attachment provides the conditions to initiate the detonation. However, the preference for the current streamlines to travel directly to the top of the substrate in both cases means that additional energy input into the detonation is limited.

Fig. 9

Magnitude of the current density (in A · m⁻²) and current streamlines in the plasma arc with (left) an aluminium substrate and (right) a low-conductivity substrate at $t={58.8}\,\upmu \hbox {s}$. The temperature in the substrate is plotted on the same scale for the two materials

4.4 Effect of a Dielectric

We place a dielectric layer of PMMA, with negligible electrical conductivity of $2.6\times 10^{-5}\,\hbox {S} \cdot \hbox {m}^{-1},$ on top of the aluminium substrate. The dielectric obeys a Mie-Grüneisen equation of state as given by Eq. (28) and parameters (29). Figure 10 shows that the dielectric layer, having a higher resistivity, restricts the arc attachment area, and thus we do not see the same expansion of the arc over the top surface of the substrate. As a result, the dielectric allows the deposition of more energy directly to the combustible gas, leading to faster ignition of the material compared to the aluminium-only case.

Fig. 10

In the left figure, a dielectric coating is placed over the aluminium substrate and leads to a larger energy deposition in the combustible gas compared to the single aluminium substrate layer. The shape of the plasma arc is also affected by the presence of the dielectric. In the right figure, the red line represents the reaction-front contour from the simulation of aluminium substrate without dielectric and the blue line the contour from the simulation of aluminium substrate with dielectric

We repeat the same setup with a low-conductivity substrate, leading to the verification that the reaction is accelerated by the effect of the dielectric, even when aluminium is replaced by a low-conductivity substrate. The respective $\lambda$ contours at times $t=6.4$, 11 and $16.8\,\upmu \hbox {s}$ are shown in Fig. 11.

Fig. 11

Contours of $\lambda =0.1$ at $t=6.4$, 11 and $16.8\,\upmu \hbox {s}$, representing the reaction-front in the combustible gas. The green line represents the contour from the simulation of the LC substrate without dielectric and the black line the contour from the simulation of the LC substrate with dielectric

4.5 Combustible Gas Sensitivity

In the previous sections, the combustible gas had an activation temperature of $8\;000\,\,\hbox {K}$. We alter its sensitivity threshold to $20\;000\,\,\hbox {K}$ and investigate the ignition process in this less sensitive combustible material. The ignition is found to be slower in the less sensitive material as expected; however, the plasma is still strong enough to ignite it directly with the initial strike. The $\lambda =0.1$ contours are shown in Fig. 12. Both simulations used an aluminium substrate without a dielectric.

Fig. 12

Contours of $\lambda =0.1$ at $t=6.4$, 11 and $16.8\,\upmu \hbox {s}$ representing the reaction-front in the combustible gas. The red line represents the contour from the simulation of an aluminium substrate (without dielectric) over a gas with activation temperature $T_{\text {A}}=8\;000\,\,\hbox {K}$ and the orange line the contour from the simulation of an aluminium substrate (without dielectric) over a gas with activation temperature $T_{\text {A}}=20\;000\,\,\hbox {K}$

5 Conclusions

In this work we present a methodology for the single-framework numerical simulation of the non-linear interaction of four states of matter: gas, liquid, solid, and plasma. In previous work we have considered the simultaneous solution of two or three states of matter and to the authors’ knowledge this work is the first time the simultaneous solution of four states of matter is achieved. Each phase can be modelled by its own set of partial differential equations (PDEs) or multi-phase diffuse-interface models can be used to combine the PDEs of multiple phases. We present the coupling of our multi-phase, diffuse-interface formulation for plasma and gases with the compressible Euler formulation describing a liquid (or other fluid) material and the elastoplastic solid formulation in an Eulerian framework. The novelty of solving simultaneously the equations for the plasma arc and another material (e.g., solid) in the same computational code should also be stressed. The basis of our algorithm is writing all the governing equations in the same, hyperbolic form, allowing all systems to be solved with (the same or distinct) finite volume methods. To track the interfaces between materials described by different governing PDE systems, we utilise level set methods. The communication between materials is achieved by solving mixed-material Riemann problems at the material interfaces. To this end, we derive mixed-material Riemann solvers for each formulation pair considered in our application. These are based on the characteristic equations derived for each system pair, allowing for the computation of the star state in the “real” material, by taking into account the two different systems on either side of the interface and applying appropriate interface boundary conditions. In summary, our multi-physics methodology follows these steps: (a) write all governing PDEs in the same mathematical form, (b) solve each PDE system using finite volume, shock-capturing methods, (c) use the level set method to track material interfaces, and (d) use the Riemann ghost fluid method and the mixed-material Riemann solvers presented in this work for communication between materials.

We apply the new methodology to study scenarios of potential ignition of combustible gases in a metal tank half-filled with liquid and half-filled with combustible gas, which is struck by lightning. We first considered a closed, cylindrical aluminium tank, half-filled with liquid and half-filled with gas, struck by lightning at the cylinder centreline. This allowed us to perform the simulations in cylindrical symmetry. It was proven in this case that, over the timescales of our simulations ($\sim 25\,\upmu \hbox {s}$), where heat conduction would not take place, the combustible material does not ignite. The pressure wave transmitted from the plasma through the substrate into the gas is weak, and the pressure does not build up enough over these timescales in the container to elevate the temperature more than a few degrees. Thus, the gas ignition threshold temperature is not reached in this scenario. We added a perforated dielectric layer over the aluminium substrate to direct the current over a smaller surface and potentially generate a funneling effect to examine whether that would lead to the ignition of the gas. Although the maximum pressures and temperatures reached in this scenario are higher than the uncoated aluminium scenario, they are still not enough to ignite the material.

We also considered a perforated aluminium substrate. This would be akin to an improper lightning protection scheme that allowed the scenario where the lightning struck and damaged the material and the same strike, or another one, hits the substrate at the same position. In this scenario, the mechanical impact of the lightning to the gas is direct and immediately ignites the gas. Replacing the aluminium with a lower conductivity material did not affect the ignition; the gas ignited immediately again and the combustion process continued with the same rate.

We added a perforated dielectric layer over the perforated metal substrate and concluded that the presence of the dielectric accelerates the combustion of the gas, both for an aluminium and a lower conductivity substrate.

Finally, replacing the combustible gas with a much less sensitive gaseous material demonstrated the deceleration of the combustion process, although this was not inhibited; the lightning strike still ignited the material directly.

The main factor that inhibited the combustion of the gaseous material was the sealing of the top surface of the metal container, suggesting that extra care should be taken in cases, where materials have been pre-damaged. Thus, our methodology can be used as part of the manufacturing process for optimising compartments in terms of shapes and materials.