Abstract
The differences between one classical and three state-of-the-art formulations of the mass density of humid air were quantified. Here, we present both the calculi for direct determination of the humid-air mass density employing the virial form of the thermodynamic equation of state, and a sufficiently accurate look-up-table for the quick-look determination of the humid-air mass density, which is based on the advanced Thermodynamic Equation of Seawater 2010.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Definition of humid air
Humid air is considered a mixture of dry air and water vapor, the mass density of which is a key meteorological observable, which depends not only on temperature and pressure but also on the water-vapor content. The latter can be expressed in different metrics such as the mass fraction of dry air in humid air, the specific humidity, the mass-mixing ratio of water vapor, the mole fraction of water vapor, the dew and frost point, or the relative humidity.
1.2 Metrological applications of the mass density of humid air
The mass density of humid air enters a wide range of metrological applications in meteorology and climatology, and is required, e.g., for the determination of turbulent fluxes of latent heat, sensible heat, and momentum as well as of radiative heating rates. A problem which does usually not take a center stage in considerations of the mass density of humid air is the correct closure of the physical conservation laws of heat, momentum (inclusive of vorticity), and mass. Violations of those conservation laws are reported to not only occur in numerical models of the atmosphere but also in the objective analysis of observational data, which enter numerical forecast systems as input parameters or which serve as a foundation for model validation and verification. For example, Trenberth et al. (1995) pointed to the existence of unclosed balances of heat, momentum and masses of air and trace gases, such as water vapor, carbon dioxide and ozone as derived from the operative global objective analysis. Due to the fact that the amount of trace gases is typically expressed in mixing ratios of mass (or volume) of the considered species relative to the mass (or volume) of air, errors in the mass balance of air can also propagate to the mass balances of climatologically effective trace gases. While the total error in the model-based mass balance of dry air alone was reported to locally cause artificial excess fluxes in the vertically integrated heat balance of up to 100W m− 2 (Alexander and Schubert 1990), the contribution of real-gas effects to this overall heat-flux error is expectable to be about four orders of magnitude lower. However, later in the present work we will demonstrate that even such tiny real-gas effect is sufficiently large to cause a climatologically relevant bias in the global energy balance.
Highly accurate mass-density formulations of humid air are also demanded for the metrology of interface parameters. Recently, Teleszewski and Gajewski (2020) employed a sophisticated experimental setup in combination with a comprehensive thermomechanical interface model for the highly accurate determination of the surface tension of water. One of the thermophysical quantities entering the calculus is the humid-air mass density. As a matter of fact, the availability of highly accurate mass-density formulations is therefore a prerequisite both for the ensurance of mass conservation in atmospheric models and for metrological tasks in meteorology and industrial applications.
1.3 On the importance of real-gas effects in humid air
Even more complicated than the treatment of hygrometric effects is the consideration of real-gas effects in humid air, which requires a virial representation of the underlying thermodynamic equation of state. Real-gas effects are small at atmospheric pressure and can be omitted in many meteorological applications of the humid-air mass density (Herbert 1987, p. 74 therein). However, several metrological tasks of meteorological interest require the consideration of real-gas effects, e.g., Buck (1981), Feistal et al. (2010a, b), Wright et al. (2010), Feistel (2012), Feistel et al. (2015a, b), Feistel et al. (2016a, b), Lovell-Smith (2006, 2007, 2009), Lovell-Smith et al. (2016), Sonntag (1990, 1994), WMO (2014), and Foken et al. (2021). The importance of real-gas effects in humid air for the energy balance of the climate system was analyzed in Feistel and Hellmuth (2020a, b).
1.4 Available mass-density formulations of humid air
The dependence of the humid-air mass density on three independent variables complicates all calculations in meteorological applications of this quantity. Established and widely employed sources for the humid-air mass density and/or its generating hygrometric quantities are the meteorological handbooks of Guyot (1852, Tables II/I and II/II “Elastic Forces of Aqueous Vapors” therein), WMO (1966), and Baur (1970, p. 471, Table 45 therein), and Herbert (1987, pp. 70–80, Tables 13, 14, and 15 therein) being part of the meteorological volume of the well-known reference book “Landolt–Börnstein”, hereafter abbreviated as LB-1987, i. e., the last publication of a look-up table for quick-look determination of the humid-air density dates back about three decades. It should be noted that the LB-1987 approach, which is presented in Section 5 here, still referred to the previous “International Practical Temperature Scale 1968” (IPTS-68). Although being more and more replaced by small computer programs, such look-up tables retain their justification as they give a very good visual overview over a per se complicated issue. Also for quick-look applications such look-up tables are still very useful. Apart from that it should be mentioned that not all of such available computer programs and mobile applications are traceably documented.
More recently, revised formulations for the humid-air mass density have been proposed on the base of the virial representation of the equation of state and the temperature scale ITS-90. The first one considered here is an air-density calculus, which is based on hygrometric expressions recommended by WMO (2014, Annex 4.B therein) for use in meteorological applications (hereafter abbreviated as WMO-2014), presented in Section 6. The second formulation is the new air-density calculus provided by the International Committee for Weights and Measures (CIPM), which is known as CIPM-2007 (Picard et al. 2008) and presented in Section 7. This equation is considered the currently most accurate available one for bouyancy corrections of high-precision weight measurements in air. However, the application of the CIPM-2007 formulation for atmospheric conditions is very limited. While its pressure definition range covers the pressure variation in the lower troposphere, its temperature definition range is restricted to typical conditions at 2m screening height above the surface in summer with a characteristic pressure of about 1000hPa. Finally, the third state-of-the-art formulation of the mass density of humid air is provided by the advanced Thermodynamic Equation of Seawater, TEOS-10 (Feistel et al 2010b, Part 1; Wright et al. 2010, Part 2; IOC et al. 2010; Feistel 2012; Feistel 2018), briefly described in Section 8. This formulation is valid for temperatures down to the temperature of homogeneous water-to-ice nucleation. CIPM-2007 and TEOS-10 are mutually consistent within their common ranges of validity to within their estimated uncertainties (Feistel 2018).
1.5 Aim and structure of the present study
In view of the availability of different formulations for the humid-air mass density the question arises for the expectable differences between them. The aim of the present analysis is an intercomparison of the LB-1987, WMO-2014, CIPM-2007, and TEOS-10 formulations of the humid-air mass density and the quantification of (i) real-gas effects in the LB-1987, WMO-2014, CIPM-2007, and TEOS-10 formulations, and (ii) the deviation of the WMO-2014, CIPM-2007, and TEOS-10 formulations from the LB-1987 reference formulation. For quick-look applications we propose a look-up table for the user-friendly determination of the humid-air mass density which is based on an approximation of the TEOS-10 formulation, and which is sufficiently accurate for the daily meteorological practice. At this place it should be noted that the redefinition of the basic thermodynamic SI properties does not affect the subsequent analysis within the given uncertainties (BIPM 2019).
The present paper is organized as follows. Section 2 contains a compilation of the elementary constants employed for the determination of the humid-air mass density. In Section 3 humidity measures are defined, which enter the formulation of the humid-air mass density as one of three independent variables, and in Section 4 the notion “virtual temperature” is introduced. Sections 5, 6, 7, and 8 are devoted to a comprehensive description of the Landolt–Börnstein (LB-1987), the WMO-2014, the CIPM-2007, and the TEOS-10 formulations of the mass density of humid air, respectively. In Section 9 a linearized TEOS-10 formulation is presented, on the base of which look-up tables for the quick-look approximation of the mass density of humid air were calculated. The uncertainty of the virial representation of humid-air mass density is analyzed in Section 10. The results of the intercomparison of the different mass-density formulations are presented in Section 11. In Section 12 climatological implications of real-gas effects in the mass density of humid air are discussed. Therein it will be shown that the tiny bias in the global energy balance caused by real-gas effects in humid air is already sufficiently large to result in a measurable global-warming signal. Finally, the present study is completed by Section 13 with the conclusions.
Appendix 1 contains details of the thermodynamic foundation of the virial representation of the mass density of humid air, and in Appendix 2 the virial coefficients of the LB-1987 approach are presented. The Supplementary Material comprises the table values evaluated in Section 11 (Hellmuth et al. 2021).
2 Elementary constants
Humid air (subscript “AV”) is described as a gas mixture with molar mass MAV, specific gas constant RAV, mole number nAV, mass mAV=nAVMAV, and mass density ϱAV, which consists
-
of dry air (subscript “A”) with molar mass MA, specific gas constant RA=R/MA, mole number nA, mass mA=nAMA, and mass density ϱA, and
-
of water vapor (subscript “V”) with molar mass MV, specific gas constant RV=R/MV, mole number nV, mass mV=nVMV, and mass density ϱV, respectively.
As a consequence of the conservation laws for mass and molecule number (molecules are treated as passive objects, i.e., chemical reactions, coagulation, sticking effects etc. are excluded), the following constraints hold:
Here, R =kBNA denotes the molar gas constant with kB being the Boltzmann constant and NA the Avogadro constant. Table 1 displays the elementary constants used in the LB-1987, WMO-2014, CIPM-2007, and TEOS-10 formulations of the humid-air mass density. The most recent value of the molar gas constant, given in last row of Table 1, is calculated using \(k_{\mathrm {B}}{=}1.380 649{\cdot }10^{-23} \text {J K}^{-1}\) and \(N_{\mathrm {A}}{=}6.022 140 76{\cdot }10^{23} \text {mol}^{-1}\) approved by the International System of Units, the SI (BIPM 2019, p. 128, Table 1 therein) as exact figures by definition.
For the subsequent derivations the following auxiliary parameters will be used, the numerical values of which are taken from Herbert (1987, Section 2.3.3, Table 12 therein):
By virtue of Eq. (2) the following relations hold:
3 Definition of humidity measures
3.1 Mole fraction, mass fraction, and mass mixing ratio of water vapor in humid air
Of particular interest for the present purposes are the mole fractions of dry air and water vapor in humid air, xA and xV, respectively, the partial pressure of water vapor in humid air, pV, the dry-air mass fraction A, the water-vapor mass fraction or specific humidity q, and the water-vapor mass mixing ratio of humid air r (Herbert 1987, Section 2.3.3, Table 12 therein):
3.2 Specific gas constant and molar mass of humid air
Employing the relations defined in Eq. (4), taking into account the general relation between the specific gas constant, the molar gas constant, and the molar mass, and considering the conservation law for the molecule number, Eq. (1), one can uniquely determine the specific gas constant RAV:
Analogously, by virtue of Eq. (5) one obtains the expression for the molar mass of humid air, MAV:
A thermodynamically rigorous derivation of commonly used humidity metrics on the base of chemical potentials can be found in Feistel et al. (2016a, b).
3.3 Relative humidity
In addition to the humidity quantities defined in Eq. (4) a further key metric is the relative humidity, RH(c), which is both a primary observable and a secondary, thermodynamically well-defined derivable as function of any of the aforementioned humidity quantities, and of T and p. The superscript “(c)” specifies the condensed phase of water the saturation state of water vapor is referring to in the thermodynamic phase equilibrium (c=w for water, c=i for ice) (see explanation given below). The relative humidity is defined by the World Meteorological Organization (WMO) as follows (WMO 2014, Eq. (4.A.15) therein):
Here, \(r_{\text {sat}}^{\text {(c)}}\), \(x_{\text {V,sat}}^{\text {(c)}}{=}p_{\text {V,sat}}^{\text {(c)}}/p\), and \(p_{\text {V,sat}}^{\text {(c)}}\) denote the mass mixing ratio, the mole fraction, and the partial pressure of water vapor in saturated humid air (subscript “sat”), respectively. The water-vapor mole fraction in saturated humid air, \(x_{\text {V,sat}}^{\text {(c)}}(T,p)\), with respect to liquid water or ice, is obtained from the condition of thermodynamic equilibrium of water in the two coexisting macrophases, i.e., in humid air and in the condensed phases of water (liquid water or ice). The thermodynamic equilibrium comprises the conditions of thermal, mechanical, and chemical equilibrium between water in the different phases. The saturated water-vapor mole fraction is obtained by solving the following two equations for the chemical equilibrium at given T and p, the first equation for the condensed phase “liquid water”, the second one for the condensed phase “ice” (Feistel et al. 2016a, Appendix C therein):
Here, \(\mu _{\mathrm {W}}^{\text {AV}}\) denotes the chemical potential of water in humid air, and μW and μIh are the chemical potentials of liquid water and ambient hexagonal ice, respectively. For the special case of pure water vapor, xV = 1, the equilibrium conditions given by Eq. (9) comprise also a regulation for the determination of the pressure of saturated (pure) water vapor (i.e., of water vapor in thermodynamic equilibrium with one of the condensed water phases), \(p=e_{\text {sat}}^{\text {(c)}}(T)\):
Equation (10) defines \(e_{\text {sat}}^{\text {(c)}}\) as a unique function of temperature. The three chemical potentials \(\mu _{\mathrm {W}}^{\text {AV}}\), μW, and μIh, together with numerical solutions of Eq. (9), \(x_{\text {V,sat}}^{\text {(w)}}\), \(x_{\text {V,sat}}^{\text {(i)}}\), and of Eq. (10), \(e_{\text {sat}}^{\text {(w)}}\), \(e_{\text {sat}}^{\text {(i)}}\), are provided by TEOS-10. Note that the solubility of air in liquid water is neglected in Eqs. (9) and (10).
3.4 Enhancement factor of water vapor in humid air
The ratio of the partial pressure of water vapor in saturated humid air, \(p_{\text {V,sat}}^{\text {(c)}}\), to the pressure of saturated (pure) water vapor, \(e_{\text {sat}}^{\text {(c)}}(T)\), defines the enhancement factor (WMO 2014, p. 160 therein) (see also see also Feistel et al. (2016a, Appendix C therein):
Having at ones disposal f(c)(T,p), one can determine both the partial pressure and the mole fraction of water vapor in saturated humid air:
The notion of enhancement factor allows the consideration of real-gas effects in the evaluation of the relative humidity as defined in Eq. (7). However, the definition of RH(c) according to Eq. (7) itself leads to a bias in the determination of the thermodynamic driving force of phase transition, which is scaled in terms of the chemical potential difference between the coexisting phases of water. In fact, the consideration of the enhancement factor to account for real-gas effects in the determination of \(x_{\text {V,sat}}^{\text {(c)}}(T,p)\) according to Eq. (12) is inconsistent with the ideal-gas definition of the relative humidity according to Eq. (7). The meteorological system of hygrometric equations, however, should in principle fulfill the axiomatic postulation of consistency as the seawater standard TEOS-10 does. To ensure a thermodynamic self-consistent description of the thermodynamic driving force, as a consequence the chemical potential difference is preferably expressed in terms of water activity and relative fugacity instead of relative humidity. The relative fugacity is a generalization of the relative humidity; it accounts for both real-gas effects in humid air and allows a thermodynamically rigorous determination of the driving force of phase transitions (e.g., Feistel 2015, 2019; Feistel et al. 2015a, b, 2016a, b; Lovell-Smith et al. 2016; Feistel and Lovell-Smith2017). In the ideal-gas approximation, relative fugacity and relative humidity are identical.
4 Definition of the virtual temperature
In order to bring the ideal-gas law for binary systems (such as for humid air) in a form as simple as those for unary systems (such as for dry air), in meteorology the temperature is usually replaced with the so-called virtual temperature as can be found in many classical textbooks and reference papers, e.g., Fleagle and Businger (1980, p. 74, Eq. (2.94) therein), Iribarne and Godson (1981, p. 74, Eq. (71) therein), Liljequist and Cehak (1984, p. 46, Section 5.2 therein), Pielke (1984, p. 8, Eq. (2.13) therein), Cotton and Anthes (1989, p. 15, Eq. (2.15) therein), Bohren and Albrecht (1998, p. 279, Eq. (6.41) therein), Pruppacher and Klett(2004, p. 106, Eq. (4.30) therein), Zdunkowski and Bott (2004, pp. 128–129 therein), Jacobson (2005, p. 33, Eq. (2.36) therein), Feistel et al. (2010a, Eq. (5.8) therein), Salby 2012, p. 129, Eq. (5.10) therein), Mölders and Kramm(2014, p. 67, Eq. (2.67) therein). Such replacement considerably simplifies the practical calculation of the humid-air mass density. The concept of virtual temperature itself, however, does not imply any approximation in the description of the behavior of binary ideal-gas mixtures but is just a “rearrangement” of the humidity information from the gas constant of the mixture to the temperature.
In its most general form the virtual temperature of humid air, Tv (subscript “v”), is defined as the temperature at which humid air with mass density ϱAV(A,T,p) at given A, T, and p would have the same mass density as dry air (corresponding to A = 1) at the same pressure:
Equation (13) can be rewritten using the compressibility factor of humid air, ZAV, defined as follows:
In Eq. (14), RAV denotes the specific gas constant of humid air according to Eq. (5), \(\widetilde {{\varrho }}_{\text {AV}}\) the molar density of humid air, and the quantity
is the mass density of humid air in ideal-gas approximation (ZAV= 1). Knowing \({\varrho }_{\text {AV}}^{\text {(id)}}\) and ZAV, the humid-air density can be calculated from Eq. (14):
The general expression of the virtual temperature is obtained from the definitions given by Eqs. (13) and (14):
Here, ZA and RA denote the compressibility factor and the specific gas constant of dry air with mass density ϱA(T,p). Applying the ideal-gas approximation, i.e., ZAV=ZA= 1, to Eq. (17) one obtains the definition of the virtual temperature in the ideal-gas limit, \(T_{\mathrm {v}}^{\text {(id)}}\), as can be found in the above-cited classical textbooks and reference papers:
The superscript “(id)” has been introduced at this place to distinguish the ideal-gas limit of the virtual temperature from its real-gas form, Eq. (17).
5 Landolt–Börnstein (LB-1987) formulation
5.1 Ideal-gas approximation of the humid-air mass density
Considering the additivity of the partial mass densities ϱA and ϱV to yield the mass density of humid air,
and approximating humid air as an ideal-gas mixture of dry air and water vapor (superscript “(id)”), one can apply Dalton’s law, according to which the total pressure p of the gas mixture is the sum of the corresponding partial pressures pA and pV of the single components (Herbert 1987, Section 2.3.3, pp. 67–68 therein) (c. f. Eq. (15)):
Here, RAV is defined in Eq. (5), by virtue of which the ideal-gas approximation of the humid-air mass density, Eq. (20), can be expressed in terms of the ideal-gas limit of the virtual temperature, Eq. (18):
Equivalently, Eq. (21) can be expressed using the virtual temperature increment, \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\):
The representation of the virtual temperature of an ideal-gas by its temperature and an excess value \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\) does not rely on an additional approximation, i.e., Eq. (22) represents a thermodynamically exact relation. For later use, we introduce here the corresponding virtual temperature increment of saturated humid air, \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}}\):
Adopting f(c)(T,p)= 1 in Eq. (12) in accordance with the ideal-gas approximation of humid air, \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}}\) given by Eq. (23) can be directly determined as a function of temperature and pressure (Herbert 1987, pp. 98–100 therein):
Alternatively to Eq. (22), \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\) can also be expressed in terms of RH(c), T, and p. By virtue of Eq. (24) one has:
Inserting now \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}} / T\) from Eq. (22), \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}} / T\) from Eq. (23), and \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}} / {{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}}\) from Eqs. (25) into Eq. (7), one arrives at the following governing equation for \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}(\text {RH}^{\text {(c)}},T,p)\) (Herbert1987, Section 2.3.3, p. 68 therein):
With \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}}(T,p)\) from Eq. (24) and RH(c) from measurements, the virtual temperature increment is fully determined by Eq. (26). The pressure of saturated water vapor, which is applied within the framework of LB-1987 approach in Eq. (24), is given by the empirical Magnus relation with the parameters presented in Table 2 (Herbert 1987, p. 98 therein):
5.2 Real-gas representation of the humid-air mass density
The real-gas form of the mass density of humid air, ϱAV, is given by Eq. (16) with the ideal-gas approximated mass density, \({\varrho }_{\text {AV}}^{\text {(id)}}\), obtained from Eqs. (21)–(27), and the compressibility factor, ZAV, defined in Eq. (14).
In Herbert (1987), two different approaches for the calculation of the compressibility factor, ZAV(xV,T,p), are described. As a first guess, Herbert (1987, p. 74 therein) approximated the compressibility factor by the one of the nitrogen gas as a proxy for a dry-air atmosphere. Details of the corresponding calculus are provided in Appendix A2.1. The assumption \(Z_{\text {AV}} {\approx } Z_{\text {N}_{2}}(T,p)\) was exploited, e.g., by Lemmon et al. (2000, Eq. (9) therein) for the calculation of air properties from high-pressure and high-temperature nitrogen data.
For a refined guess, Herbert (1987, Section 2.3.3, Table 15 therein) presented table values of ZAV for a binary dry air–water vapor mixture, however, without explicit specification of the underlying formula. Therefore, in Appendix A2.2 we have traced back the available information to the sources underlying the calculus of the virial representation of ZAV(xV,T,p).
The availability of alternative representations of the virial coefficients for both pure nitrogen gas as well as for the dry air–water vapor mixture suggests a corresponding update of the formulation of the compressibility factor. Here, however, we want to focus our interest on the recovery of the original LB-1987 calculus as the reference formulation of the mass density of humid air. A detailed intercomparison of different formulations for the virial coefficients is beyond the scope of the present analysis but subject of an ongoing work.
By virtue of Eqs. (7) and (12), the water-vapor mole fraction in humid air, xV, appearing in ZAV(xV,T,p) (see Eq. (A2.5)), can be expressed in terms of the relative humidity:
For quick-look applications, Herbert (1987) prepared three look-up tables for the stepwise determination of the mass density of humid air with liquid water serving as the condensed phase of water (c=w):
-
1.
The first look-up table contains the virtual temperature increment \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}} = T_{\text {v,sat}}^{\text {(id,c)}}-T\) of saturated humid air as a function of Celsius temperature 𝜗 in the interval − 40°C≤𝜗≤ 50°C with a resolution of Δ𝜗 = 1K, and of pressure p in the interval 1100hPa≥p≥ 200hPa with a resolution of Δp = 50hPa (Herbert1987, pp. 70–73, Table 13 therein). Having determined \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,c)}}\), the actual virtual temperature increment \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\) is calculated using either the full \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\) expression given by Eq. (26), or the following approximation:
$$ \begin{array}{@{}rcl@{}} {{\varDelta}} T_{\mathrm{v}}^{\text{(id)}} & = & \frac{\text{RH}^{(\mathrm{c})} {{\varDelta}} T_{\text{v,sat}}^{\text{(id,c)}}}{1 + (1-\text{RH}^{(\mathrm{c})}) \frac{{{\varDelta}} T_{\text{v,sat}}^{\text{(id,c)}}}{T}}\\ & \approx & \text{RH}^{(\mathrm{c})} {{\varDelta}} T_{\text{v,sat}}^{\text{(id,c)}} \left[ 1 - (1-\text{RH}^{(\mathrm{c})}) \frac{{{\varDelta}} T_{\text{v,sat}}^{\text{(id,c)}}}{T} \right]\\ & \approx & \text{RH}^{(\mathrm{c})} {{\varDelta}} T_{\text{v,sat}}^{\text{(id,c)}} \left[ 1 - \frac{{{\varDelta}} T_{\text{v,sat}}^{\text{(id,c)}}}{T} \right]. \end{array} $$(29)According to Herbert (1987, p. 68 therein), the \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\) expression given by Eq. (29) will generally suffice for practical applications, because the neglect of the \(\left [ \text {RH}^{(\mathrm {c})} \right ]^{2}\) term is always less than 0.1K as long as \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}{\le } 10 \mathrm {K}\).
-
2.
The second look-up table presents the mass density of humid air in ideal-gas approximation, \({\varrho }_{\text {AV}}^{\text {(id)}}\), as a function of the virtual Celsius temperature 𝜗v in the interval − 110°C≤𝜗v≤ 100°C with a resolution of Δ𝜗v= 1K, and of pressure p in the interval 1100hPa≥p≥ 100hPa with a resolution of Δp = 100hPa (Herbert1987, pp. 76–79, Table 14 therein).
-
3.
The third look-up table presents the compressibility factor \(Z_{\text {AV}{=}}{\varrho }_{\text {AV}}^{\text {(id)}}/{\varrho }_{\text {AV}}\) (a) for dry air as a function of pressure p at p =(0,300, 700,1100)hPa and of Celsius temperature in the interval − 100°C≤𝜗≤− 10°C with a resolution of Δ𝜗 = 10K, and (b) for humid air as a function of pressure p at p =(0,300,700,1100)hPa, of Celsius temperature in the interval 0°C ≤ 𝜗 ≤ 60°C with a resolution of Δ𝜗 = 10K, and of the relative humidity RH(c) in the interval 0%rh≤RH(c)≤ 100%rh with a resolution of Δ RH(c)= 25%rh (Herbert 1987, p. 80, Table 15 therein). Knowing the ideal-gas mass density \({\varrho }_{\text {AV}}^{\text {(id)}}\) from steps 1 and 2, the real-gas mass density is given by \({\varrho }_{\text {AV}}{=}{\varrho }_{\text {AV}}^{\text {(id)}}/Z_{\text {AV}}\).
6 WMO-2014-compatible formulation
6.1 Basic information
The second formulation of the humid-air mass density considered here is based on hygrometric expression recommended by WMO (2014, Annex 4.B therein) for use in meteorological applications. These expressions, in turn, are those proposed by Sonntag (1990, 1994), which rely on values from the compilation of a consistent set of fundamental physical constants of 1986 with completion by that author. The saturation vapor pressures with respect to water and ice are described by the Magnus formula, the parameters of which have been recalculated by Sonntag (1990) from the previous IPTS-68 to the currently valid “International Temperature Scale” (ITS-90). On recommendation of the Consultative Committee on Thermometry (CCT) the ITS-90 was adopted in 1989 and introduced on 1 January 1990 by the International Committee on Weights and Measures (CIPM), authorized by the CIPM (Sonntag 1990, 1994). ITS-90 will remain a valid temperature scale for the foreseeable future in parallel to the recent “thermodynamic temperature” introduced by the revised SI in 2018.
Actually, neither Sonntag (1990, 1994) nor WMO (2014) provided an explicit formula for the mass density of real humid air, which implies instead the adoption of the ideal-gas approximation of this quantity. However, the hygrometric formulae proposed in the cited references allow the determination of the humid-air mass density with approximative consideration of real-gas effects.
6.2 Assumptions, approximations, and mass-density formulation
In order to derive an approximative expression for the mass density of humid air, in the following use is made (i) of the additivity of the single-component mass densities in the binary mixture according to Eq. (19), (ii) of the real-gas representation of the thermal equations of state for dry air and water vapor, (iii) of the approximative additivity of the partial pressures pA and pV to yield the total pressure p according to Dalton’s law, implying the disregard of interactions between dry-air and water-vapor molecules. Introducing the apparent specific gas constants \(R_{\mathrm {A}}^{\prime }\) and \(R_{\mathrm {V}}^{\prime }\), which account for real-gas effects caused by air-air and water-water molecular interactions (see Bögel 1977; Sonntag 1990, Table 1 therein; Sonntag and Zeitschrift1994, Eqs. (3), (4) therein), the approximative gas law of humid air reads:
Here, ZA and ZV denote the compressibility factors of dry air and water vapor, respectively, and \(R_{\text {AV}}^{\prime }\) is the apparent specific gas constant of the real-gas mixture.
The real-gas representation given by Eq. (30) is formally identical with the ideal-gas approximation of humid air, Eq. (20), which will allow us to apply the calculus of the LB-1987 ideal-gas formulation, presented in Section 5.1 but with parameter modifications, also for the calculation of the mass density of real humid air. For completeness, these modifications are presented hereafter. By virtue of
and by replacement of the auxiliary parameters introduced by Eq. (2) with their real-gas corrected counterparts
one can formally apply the derivations given by Eqs. (21)–(26) to obtain the apparent specific gas constant of the real-gas mixture, Eq. (5),
and the governing equation for the mass density of humid air:
Equivalently, Eq. (34) can be expressed using the virtual temperature increment, \({{\varDelta }} T_{\mathrm {v}}^{\prime }\), analogously to Eq. (22)–(26):
Alternatively to the use of Eqs. (31)–(35), the modified ideal-gas form of the mass density of humid air given by Eq. (30) can also be expressed in the equivalent real-gas form given by Eq. (14) if the compressibility factor ZAV is used in the following approximative form:
In the derivation of Eq. (36) use was made of Eqs. (2) and (5).
6.3 Thermodynamic closure parameters
In order to close the calculus, the compressibility factors, ZA and ZV, and the expression for the water-vapor mole fraction in saturated humid air, \(x_{\text {V,sat}}^{\text {(c)}}\), must be specified. The compressibility factor ZA is specified according to Bögel (1977), and ZV according to Sonntag (1990):
The quantity \(x_{\text {V,sat}}^{\text {(c)}}(T,p)\) is given by Eq. (12) with the saturation vapor pressure of water, \(e_{\text {sat}}^{\text {(c)}}(T)\), according to the Magnus formula, Eq. (27). The corresponding constants are displayed in Table 3 (Sonntag 1990, Eqs. (2), (8) therein).
With neglect of the temperature dependence, Sonntag (1990, Eq. (20) and reference therein to Sonntag 1989) proposed the following approximation of the enhancement factors for both liquid water (c=w) and ice (c=i) as developed by Bögel (1977):
Figure 1 depicts the enhancement-factor deviation from ideality, Δf = f(c)(p) − 1. Upon increasing dilution of the humid-air mixture (p → 0), the gas increasingly behaves like an ideal gas, characterized by weakening of the molecular interactions between the gas constituents. In this case the enhancement-factor deviation tends to approach zero. Upon increasing pressure, molecular interactions starts to come into play and the gas behavior deviates more and more from ideality. In the atmospheric pressure range the enhancement-factor deviation according to Eq. (38) varies in the range of Δf(c)(p) ≈ (1 − 5)‰.
Enhancement-factor deviation from ideality, Δf(c) = f(c)(p) − 1, according to Eq. (38) as function of pressure
By virtue of Eq. (38), the mass density of humid air is given by Eq. (34) with \(R_{\mathrm {A}}^{\prime }\) from Eqs. (30) and (37), \(T_{\mathrm {v}}^{\prime }\) from Eq. (35) with \(x_{\text {V,sat}}^{\text {(c)}}\) from Eq. (12), \(e_{\text {sat}}^{\text {(c)}}(T)\) from Eq. (27) and Table 3, and f(c)(p) from Eq. (38).
7 CIPM-2007 formulation
Based on gravimetric density measurements and using the CIPM-81/91 formula, Picard et al. (2008) determined an equation of state for the mass density of humid air, known as CIPM-2007 formulation, for application in the following pressure and temperature ranges:
The density of real humid air, ϱAV, is determined on the base of Eqs. (14) and (18) with the water-vapor mole fraction xV=xV(RH,T,p) determined using Eq. (28) and the molar gas constant and the molar masses of dry air and water vapor as given in Table 1 (Picard et al. 2008, Eqs. (1), (A1.3), and Table 4 therein):
The enhancement factor defined by Eq. (11) and entering Eq. (28) for the determination of xV(RH,T,p), is parameterized as follows (Picard et al. 2008, Appendix A, Eq. (A1.2) therein):
The pressure of saturated water vapor is given by the following parameterization (Picard et al. 2008, Eq. (A1.1) therein):
Finally, the CIPM-2007 formulation of the compressibility factor, ZAV, reads (Picard et al. 2008, Eq. (A1.4) therein):
8 TEOS-10 formulation
8.1 Background information
The Thermodynamic Equation Of Seawater 2010 (TEOS-10) is an international standard for the thermodynamic properties of seawater, ice, and humid air, which was adopted in 2009 by the Intergovernmental Oceanographic Commission (IOC) of the UNESCO and in 2011 by the International Union of Geodesy and Geophysics (IUGG). This new standard is based on the realization of a very general algorithm to describe thermodynamic systems: (1) formulation of the fundamental thermodynamic relation of the system of interest; (2) determination of a suitable thermodynamic potential (containing by definition all information about the system) from experimental data or on the base of microscopic theories within the framework of statistical thermodynamics; (3) calculation of the thermodynamic properties, the thermic and caloric equations of state, and all other state variables of interest from the thermodynamic potential (Kluge and Neugebauer 1994). The application of the TEOS-10 seawater standard is supported by a comprehensive, open-access source code library, referred to as the Sea-Ice-Air (SIA) library. The background information and equations (including references for the primary data sources) required for the determination of the properties of single phases, material components, phase transitions, and composite systems as implemented in the SIA program library are presented in the key papers of Feistel et al. (2010a, 2010b) and Wright et al. (2010), the TEOS-10 Manual (IOC et al. 2010), the introductory and guidance paper of Feistel (2012), and a comprehensive review paper of Feistel (2018). The SIA program library can be downloaded from the official TEOS-10 website (http://www.teos-10.org/).
8.2 Thermodynamic foundation
TEOS-10 is based on four independent thermodynamic potentials, defined as functions of the independent observables temperature, pressure, dry-air mass fraction, density, and salinity. A description of the theoretical background is given in Appendix 1.
The IAPWS-95 fluid water formulation is of key importance for the description of atmospheric water within the framework of TEOS-10. This water formulation is based on the international temperature scale ITS-90 and on the evaluation of a comprehensive and consistent data set, which was assembled from a total of about 20,000 experimental data of water. The authors of IAPWS-95 (Wagner and Pruß 2002) took into account all available information given in the scientific articles, which described the data collection underlying the development of the thermal equation of state of water. They critically reexamined the available data sets w.r.t. their internal consistency and their basic applicability for the development of a new equation of state for water. Only those data were incorporated into the final nonlinear fitting procedure, which were judged to be of high quality. These selected data sets took into account experimental data, which were available by the middle of the year 1994 (Wagner and Pruß 2002). A compilation of the experimental data used to develop IAPWS-95 can be found on the official IAPWS website (http://www.iapws.org/).
The availability of reliable experimental data on subcooled liquid water (i.e., metastable w.r.t. the solid form of water) was restricted to a few data sets for several properties only along the isobar p = 1013.25hPa, which set the lower limit of the temperature range for the validity of IAPWS-95 for liquid water (and so of TEOS-10) to T = 236K. This temperature is called the temperature of homogeneous ice nucleation (or homogeneous freezing temperature) and represents the lower limit below which it is very difficult to subcool water. The assessment of the accuracy of the IAPWS-95 formulation in the temperature range of subcooled liquid water (see Wagner and Pruß2002, Section 7.3.2 therein) revealed that TEOS-10 fully satisfies the meteorological needs with respect to accuracy down to this temperature. In contrast to the water formulation, the water-vapor formulation of IAPWS-95 (and TEOS-10) is valid down to 130K, and with an available extension (see IAPWS G9-12 2012 and Feistel et al. 2010a) even to 50K.
8.3 Governing equation for the humid-air mass density
For given A, T, and p the TEOS-10 mass density of humid air ϱAV(A,T,p) is iteratively calculated from the following transcendental implicit equation Feistel et al.(2010b, Eq. (4.38) therein):
Here, \(f_{\text {AV}} \left (A,T,{\varrho }_{\text {AV}} \right )\) denotes the specific Helmholtz energy of humid air, the thermodynamic foundation of which is presented in Appendix 1. For given A, T, and p, the humid-air density ϱAV can be determined by numerical solution of the transcendental Eq. (43) using the SIA library function air\(\underline { }\textit {g}\underline { }\textit {density}\underline { }\)si(a,t,p) (see Feistel et al. 2010b (digital supplement, Table S12 therein) and Wright et al.2010 (digital supplement, Table S16, Eq. (S16.6) therein)).
9 Linearized TEOS-10 formulation for quick-look applications
9.1 Taylorization of the expression for the humid-air mass density
For many practical applications the precalculation of look-up-tables of the humid-air mass density might be a suitable alternative to the numerical execution of the TEOS-10 SIA library function to solve Eq. (43). To avoid an unhandily large look-up table of the mass density of humid air originating from sampling the parameter space in the three independent variables A, T, and p, here a linearization of the TEOS-10 formulation given by Eq. (43) will be proposed, which allows the determination of ϱAV(A,T,p) from one look-up table containing the virtual temperature increment of saturated humid air, \({{\varDelta }} T_{\text {v,sat}}^{\text {(c)}}(T,p)\), and a second look-up table containing the mass-density of dry air, ϱA(T,p)=ϱAV(1,T,p). The approach is similar to the one in Herbert (1987, Tables 13–15 therein) but requires only two look-up tables instead of three.
Starting point is the definition of the virtual temperature of humid air, Tv, according to Eqs. (13) and (17), respectively, i.e., the ideal-gas approximation was omitted in the following steps. Employing the relation A =A(xV), the definition of the virtual temperature reads:
By virtue of the WMO definition of the relative humidity, Eq. (7),
the linearization of the left-hand side of Eq. (44) reads:
Here, δϱAV(T,p) is an infinitesimal excess value of the mass density, which must be sufficiently small to justify the approximation of the mass density of humid air by a linear function of the relative humidity at constant temperature and pressure. The relation holds exactly at both RH(c)= 0 and RH(c)= 1.
In the ideal-gas presentation underlying Eq. (22), the virtual temperature of ideal humid air \(T_{\mathrm {v}}^{\text {(id)}}\) was represented by a superposition of the temperature T and a virtual temperature increment \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\). In contrast to Eq. (22), the following analysis is based on the real-gas representation given by Eq. (44), i.e., the virtual temperature of the real gas, Tv, is approximated by a superposition of temperature T and an infinitesimal temperature increment δTv. While \({{\varDelta }} T_{\mathrm {v}}^{\text {(id)}}\) has been introduced as an exact incremental value without any constraint on its absolute value, the infinitesimal quantity δTv is demanded to be sufficiently small to allow the expansion of the mass density of dry air into a Taylor series (“taylorization”) up to the linear term (linearization). Employing the decomposition
the linearization of the right-hand side of Eq. (44) reads:
By virtue of the definition of the coefficient of isobaric thermal expansion of dry air, \(\alpha _{p} \left (T,{\varrho }_{\text {AV}}(0,T,p) \right )\),
Equation (47) assumes the following form:
The thermal expansion coefficient in Eq. (48) can be numerically determined by means of the TEOS-10 SIA library function air\(\underline { }\textit {f}\underline { }\textit {expansion}\underline { }\)si(a,t,d) (Feistel et al. 2010b, digital supplement, Table S5 therein; Wright et al. 2010, digital supplement, Table S10, Eq. (S10.6) therein). Inserting Eqs. (45) and (48) into Eq. (44), one obtains the virtual temperature increment:
9.2 Construction of look-up tables for quick-look applications
The virtual temperature increment of saturated humid air, \(\delta T_{\text {v,sat}}^{\text {(c)}}(T,p)\), and the mass density of dry air, ϱAV(0,T,p), were calculated using the TEOS-10 SIA library, stored in two separate look-up tables with isotherms arranged along the rows (𝜗 =− 40…60°C, Δ𝜗 = 1K), isobars arranged in the columns (p = 200 − 1100hPa, Δp = 50hPa), and published in Foken et al. (2021, Tables 5.17–5.20 therein).
Based on these two look-up tables, the mass density of humid air can be determined for given RH, T, and p in three steps:
-
1.
At first, for given T and p the quantity \(\delta T_{\text {v,sat}}^{\text {(c)}}(T,p)\) is read out from the first look-up table.
-
2.
At second, the virtual temperature increment \(\delta T_{\mathrm {v}}(\text {RH}^{(\mathrm {c})},T,p)\) is calculated according to Eq. (49), and therewith the virtual temperature Tv according to Eq. (46):
$$ T_{\mathrm{v}} = T + \delta T_{\mathrm{v}}(\text{RH}^{(\mathrm{c})},T,p) . $$ -
3.
At third, for given Tv and p the mass density of humid air, ϱAV(0,Tv,p), can be directly readout from the second look-up table at T =Tv.
As real-gas effects are already considered by the virial representation of the mass density of humid air in TEOS-10, the present approach employs Tv instead of \(T_{\mathrm {v}}^{\text {(id)}}\) and, as a consequence, does not require a third look-up table for the compressibility factor as in the Landolt–Börnstein approach.
10 Uncertainty analysis
While for the LB-1987 and WMO-2014 formulations of the humid-air mass density no uncertainty is provided, Picard et al. (2008, Table 2 therein) notified for the CIPM-2007 formulation a combined standard uncertainty of u(ϱAV)/ϱAV= 22ppm (exclusive additional contributions originating from instrumental uncertainties due to measured input pressure, temperature, dew-point temperature or relative humidity, and the mole fraction of CO2). To get a clue of the combined standard uncertainty of the TEOS-10 formulation we start with Eq. (14) and assume it prudent that the uncertainty of the mass density is controlled by those of the compressibility factor, u(ϱAV)/ϱAV≈u(ZAV)/ZAV. By virtue of u(ZAV)/ZAV≤ 20ppm in line with Picard et al. (2008) and references therein one can conclude that the combined standard uncertainty of the TEOS-10 humid-air mass density is of the same order of magnitude as that of the CIPM-2007 formulation.
11 Results: intercomparison of the different mass-density formulations
11.1 Specification of the condensed phase for the calculations
The intercomparison of the different mass-density formulations has been consistently conducted taking “liquid water” as the thermodynamic reference phase (saturation state of water in humid air with respect to condensed water, denoted by superscript c=w). At 𝜗 > 0°C this refers to thermodynamically stable water, and at 𝜗 ≤ 0°C to undercooled (metastable) water. However, to disburden the type face the superscript (w) is omitted hereafter in the symbols RH and ΔTv,sat.
11.2 LB-1987, WMO-2014, CIPM-2007, and TEOS-10 mass densities of saturated humid air
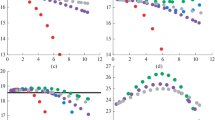
Tables 4 and 5 display the mass density of saturated humid air in ideal-gas approximation, \({\varrho }_{\text {AV}}^{(\text {id,sat)}}(\text {RH=100 \%rh},T,p)\), at p = 1000 hPa (second column) together with the relative deviations (in percent) \(\left ({\varrho }_{\text {AV}}^{\text {(X)}}-{\varrho }_{\text {AV}}^{\text {(id)}} \right ) /{\varrho }_{\text {AV}}^{\text {(id)}}\) of the X = (LB-1987, WMO-2014, CIPM-2007, TEOS-10) formulations from the ideal-gas approximation (third to sixth column) at atmospheric pressure, (a) in the temperature range of the CIPM-2007 formulation (Table 4), (b) in the temperature range − 35 ≤ 𝜗/°C ≤ 60 (Table 5). The graphs corresponding to Tables 4 and 5 are depicted in Figs. 2 and 3.
Mass density of saturated humid air in ideal-gas approximation, \({\varrho }_{\text {AV}}^{\text {(id,sat)}}(\text {RH=100 \%rh},T,p)\), at p = 1000hPa and relative deviations (in percent) \(\left ({\varrho }_{\text {AV}}^{\text {(X,sat)}}-{\varrho }_{\text {AV}}^{\text {(id,sat)}} \right ) /{\varrho }_{\text {AV}}^{\text {(id,sat)}}\) of the X = (LB-1987, WMO-2014, CIPM-2007, TEOS-10) formulations from the ideal-gas approximation in the validity range of the CIPM-2007 formulation according to Table 4
By virtue of the definition provided by Eq. (14), the values presented in Table 5, \(\left ({\varrho }_{\text {AV}}^{\text {(X,sat)}}-{\varrho }_{\text {AV}}^{\text {(id,sat)}} \right ) /{\varrho }_{\text {AV}}^{\text {(id,sat)}}\), can be used to calculate the compressibility factor of saturated humid air:
To get an idea of the order of magnitude of the compressibility factor, Fig. 4 depicts the compressibility-factor deviation from ideality, \({{\varDelta }} Z_{\text {AV}}^{\text {(sat)}}=Z_{\text {AV}}^{\text {(sat)}}-1\). Throughout the considered temperature range one has \({{\varDelta }} Z_{\text {AV}}^{\text {(sat)}}<0\) resulting in \(Z_{\text {AV}}^{\text {(sat)}} < 1\), i.e., the dominating molecular forces are attractive. While the three analyzed mass-density formulations fairly agree with respect to their compressibility factors below 40°C, the WMO-2014 formulation reveals a smaller real-gas effect at 𝜗 > 40°C than the LB-1987 and TEOS-10 formulations. This originates from the approximations entering the WMO-2014 formulation by Eqs. (30) and (37).
Compressibility-factor deviation \({{\varDelta }} Z_{\text {AV}}^{\text {(sat)}}=Z_{\text {AV}}^{\text {(sat)}}-1\) for saturated humid air with \(Z_{\text {AV}}^{\text {(sat)}}\) according to Eq. (50) and \(\left ({\varrho }_{\text {AV}}^{\text {(X,sat)}}-{\varrho }_{\text {AV}}^{\text {(id,sat)}} \right ) / {\varrho }_{\text {AV}}^{\text {(id,sat)}}\) from Table 5 for the X = (LB-1987, WMO-2014, TEOS-10) formulations in the temperature range − 35 ≤ 𝜗/°C ≤ 60
As shown in Table 4, at atmospheric pressure and room temperature the analyzed mass densities of saturated humid air deviate from the ideal-gas limit by ≈ 0.05%. For comparison, this relative deviation in the mass densities is in the order of magnitude of the relative deviation in the saturation water-vapor pressure solely originating from choice of the temperature scale (IPTS-68 vs. ITS-90). For example, Sonntag (1990, Table 3 therein) reported
increasing to |− 0.055|% at 𝜗90= − 30°C and to 0.073% at 𝜗90= 60°C. Toward the lower and upper limits of the temperature range in Table 5, the relative deviation due to real-gas effects may exceed ≈ 0.1%. As a consequence, for hygrometric applications in which differences originating from the choice of the temperature scales play a role with respect to the required accuracy, the consideration of real-gas effects in the mass-density determination is mandatory. Note that CIPM-2007 formulation permits an adjustable value for the CO2 fraction of dry air, while CO2 is entirely neglected in the dry-air model of TEOS-10 (Lemmon et al. 2000).
11.3 Reexamination of the LB-1987 formulation
In order to check the consistency between the analytical LB-1987 calculus of the humid-air mass density recovered here and presented in Section 5 and the corresponding look-up table values previously published in Herbert (1987, Tables 13–15), we have determined and evaluated the relative deviations of the calculated from the published values.
-
The Supplementary Material (SM), Table S-1 contains the virtual temperature increments of saturated humid air (serving as reference values), \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,LUT)}}(T,p)\) (superscript “LUT” for look-up table), excerpted from the corresponding look-up table published in Herbert (1987, Table 13 therein). Compared to the original look-up table the temperature resolution was reduced here to 5K and the pressure resolution to 100hPa, respectively. SM/Table S-2 displays the relative deviations, \(\left ({{\varDelta }} T_{\text {v,sat}}^{\text {(id,calc)}{-}}{{\varDelta }} T_{\text {v,sat}}^{\text {(id,LUT)}} \right )/ {{\varDelta }} T_{\text {v,sat}}^{\text {(id,LUT)}}\) (in percent), of the calculated values \({{\varDelta }} T_{\text {v,sat}}^{\text {(id, calc)}}\) using Eq. (24), from the look-up table reference values \({{\varDelta }} T_{\text {v,sat}}^{\text {(id,LUT)}}\) presented in SM/Table S-1. The maximum of the absolute value of the relative deviation was found to amount ≈ 28% at 𝜗 =− 40°C and p = 1100hPa, i.e., at extremely dry conditions corresponding to very low \({{\varDelta }} T_{\text {v,sat}}^{\text {(id)}}\) values. These enhanced deviations are supposed to originate from round-off errors.
-
SM/Table S-3 shows the ideal-gas approximated dry-air mass densities (serving as reference values), \({\varrho }_{\mathrm {A}}^{\text {(id,LUT)}}(T,p)\), excerpted from the corresponding look-up table in Herbert(1987, Table 14 therein). Compared to the original look-up table, the temperature resolution was reduced to 5K. SM/Table S-4 displays the relative deviations, \(\left ({\varrho }_{\mathrm {A}}^{\text {(id,calc)}}-{\varrho }_{\mathrm {A}}^{\text {(id,LUT)}} \right )/ {\varrho }_{\mathrm {A}}^{\text {(id,LUT)}}\) (in percent), of the calculated values \({\varrho }_{\mathrm {A}}^{\text {(id,calc)}}\) employing Eq. (20), from the look-up table reference values \({\varrho }_{\mathrm {A}}^{\text {(id,LUT)}}\) presented in SM/Table S-3. The maximum of the absolute value of the relative deviation was found to amount only ≈ 0.05%.
-
SM/Table S-5, column 3 presents the compressibility factors of dry air (serving as reference values), \(Z_{\mathrm {A}}^{\text {(LUT)}}(T,p)=\) \(Z_{\text {AV}}^{\text {(LUT)}}(x_{\mathrm {V}}=0,T,p)\), excerpted from the corresponding look-up table in Herbert(1987, Table 15, left panel therein). SM/Table S-5, column 4 depicts the relative deviations, defined by \(\left (Z_{\mathrm {A}}^{\text {(calc)}}{-}Z_{\mathrm {A}}^{\text {(LUT)}} \right )/ Z_{\mathrm {A}}^{\text {(LUT)}}\) (in percent), of the calculated values \(Z_{\mathrm {A}}^{\text {(calc)}}\) according to the Goff–Gratch formulation using Eq. (A2.4), from the look-up table values \(Z_{\mathrm {A}}^{\text {(LUT)}}(T,p)\), presented in SM/Table S-5, column 3. The maximum of the absolute value of the relative deviation was found to amount only ≈ 0.44%.
-
Finally, SM/Table S-6 shows the compressibility factors of humid air (serving as reference values), \(Z_{\text {AV}}^{\text {(LUT)}}(\text {RH},T,p)\), excerpted from the corresponding look-up table in Herbert (1987, Table 15, right panel therein) for RH=(0,25,50, 75,100)%rh. In SM/Table S-7 presented are the relative deviations, defined by \(\left (Z_{\text {AV}}^{\text {(calc)}}{-}Z_{\text {AV}}^{\text {(LUT)}} \right )/ Z_{\text {AV}}^{\text {(LUT)}}\) (in percent), of the calculated values \(Z_{\text {AV}}^{\text {(calc)}}\) using Eq. (A2.4) from the look-up table values \(Z_{\text {AV}}^{\text {(LUT)}}\), depicted in SM/Table S-6. The maximum of the absolute value of the relative deviation was found to amount only ≈ 0.02%.
The analysis confirms the consistency between the analytical LB-1987 formulation of the humid-air mass density with the look-up table values published in Herbert (1987, Tables 13-15 therein).
11.4 Quantification of real-gas effects for 600 ≤ p/hPa ≤ 1100 and 15 ≤ 𝜗/°C ≤ 27
SM/Table S-8 displays the ideal-gas approximation of the humid-air mass density (serving as the reference formulation), \({\varrho }_{\text {AV}}^{\text {(id)}}(\text {RH},T,p)\) according to Eq. (20) (in units of kg m− 3), over the validity range of the CIPM-2007 formulation (see Section 7). In SM/Tables S-9 to S-12 shown are the relative deviations \(\left ({\varrho }_{\text {AV}}^{\text {(X)}}{-}{\varrho }_{\text {AV}}^{\text {(id)}} \right )/ {\varrho }_{\text {AV}}^{\text {(id)}}\) (in percent) of the respective LB-1987, WMO-2014, CIPM-2007 and TEOS-10 mass densities, \({\varrho }_{\text {AV}}^{\text {(X)}}\) with X = (LB87, WMO, CIMP, TEOS), from the ideal-gas approximation, \({\varrho }_{\text {AV}}^{\text {(id)}}\) presented in SM/Table S-8. The maximum of the absolute value of the relative deviation was found to amount ≈ 0.06% and to occur for the WMO-2014 formulation.
11.5 Deviations from the LB-1987 real-gas formulation for 600 ≤ p/hPa ≤ 1100 and 15 ≤ 𝜗/°C ≤ 27
SM/Table S-13 displays the LB-1987 humid-air mass density (serving as the reference formulation), \({\varrho }_{\text {AV}}^{\text {(LB87)}}(\text {RH},T,p)\) (in units of kg m− 3), over the validity range of the CIPM-2007 formulation (see Section 7). SM/Tables S-14 to S-16 show the relative deviations \(\left ({\varrho }_{\text {AV}}^{\text {(X)}}{-}{\varrho }_{\text {AV}}^{\text {(LB87)}} \right )/ {\varrho }_{\text {AV}}^{\text {(LB87)}}\) (in percent) of the respective WMO-2014, CIPM-2007, and TEOS-10 mass densities, \({\varrho }_{\text {AV}}^{\text {(X)}}\) with X = (WMO, CIMP, TEOS), from the LB-1987 real-gas formulation, \({\varrho }_{\text {AV}}^{\text {(LB87)}}\), respectively. The maximum of the absolute value of the relative deviation was found to amount only ≈ 0.01% and to occur for the WMO-2014 formulation.
11.6 Deviation of the approximative from the full real-gas LB-1987 formulation under tropospheric conditions
SM/Table S-17 displays the LB-1987 humid-air mass density (serving as the reference formulation), \({\varrho }_{\text {AV}}^{\text {(LB87)}}(\text {RH},T,p)\) (in units of kg m− 3), using the Goff–Gratch formulation of the compressibility factor (full formulation), Eq. (A2.4), in the pressure range 200hPa≤p≤ 1100hPa, temperature range − 35°C≤𝜗≤ 60°C, and at relative humidities RH=(0,25,50,75,100)% rh. SM/Table S-18 shows the relative deviation, \(\left ({\varrho }_{\text {AV}}^{\text {(LB87,approx)}}{-}{\varrho }_{\text {AV}}^{\text {(LB87)}} \right ) / {\varrho }_{\text {AV}}^{\text {(LB87)}}\) (in percent), of the approximative LB-1987 values \({\varrho }_{\text {AV}}^{\text {(LB87,approx)}}\) employing the compressibility factor for nitrogen, \(Z_{\text {N}_{2}}\) according to Eq. (A2.1), from the LB87 values \({\varrho }_{\text {AV}}^{\text {(LB87)}}\) using the Goff–Gratch formulation of ZAV according to Eq. (A2.4). The maximum of the absolute value of the relative deviation was found to amount ≈ 2.6%.
11.7 Deviations of the WMO-2014 and TEOS-10 from the LB-1987 real-gas formulation
SM/Table S-19 and SM/Table S-20 present the relative deviations, defined by \(\left ({\varrho }_{\text {AV}}^{\text {(X)}}{-}{\varrho }_{\text {AV}}^{\text {(LB87)}} \right ) / {\varrho }_{\text {AV}}^{\text {(LB87)}}\) (in percent), of the WMO-2014 and TEOS-10 values \({\varrho }_{\text {AV}}^{\text {(X)}}\) with X = (WMO, TEOS) from the LB-1987 values \({\varrho }_{\text {AV}}^{\text {(LB87)}}\) using ZAV according to Eq. (A2.4), presented in SM/Table 17. An excerpt of these tables is shown in Table 6.
The maximum of the relative deviation of the WMO-2014-based from the LB-1987 formulation was found to amount − 0.1297%, occurring at p = 400hPa, 𝜗 = 60°C, and RH = 100% rh, that of the TEOS-10 formulation to amount 0.1939%, occurring at p = 200hPa, 𝜗 = 60°C, and RH = 100% rh.
11.8 Deviation of the WMO-2014 from the TEOS-10 formulation
SM/Table S-21 displays the relative deviation, \(\left ({\varrho }_{\text {AV}}^{\text {(WMO)}}{-}{\varrho }_{\text {AV}}^{\text {(TEOS)}} \right ) / {\varrho }_{\text {AV}}^{\text {(TEOS)}}\) (in percent), of the WMO-2014-based values \({\varrho }_{\text {AV}}^{\text {(WMO)}}\) from the TEOS-10 values \({\varrho }_{\text {AV}}^{\text {(TEOS)}}\). An excerpt of this table is shown in Table 7. The maximum relative deviation of the WMO-2014 formulation from the TEOS-10 formulation was found to amount − 0.2701%, occurring at p = 200hPa and 𝜗 = 60°C, and RH = 100% rh.
11.9 Look-up table of the approximative TEOS-10 humid-air mass density
-
(i)
SM/Table S-22 depicts (a) the approximative virtual temperature increment of saturated humid air ΔTv,sat(T,p), derived from the linearized TEOS-10 formulation of ϱAV(xV,T,p) according to Eq. (49), and (b) the real-gas dry-air mass density, ϱA(T,p)=ϱAV(xV= 0,T,p). Having determined the virtual temperature, Tv=T + RHΔTv,sat(T,p), one can directly obtain the mass density of real-gas humid air as ϱAV(RH,T,p)=ϱA(Tv,p). SM/Table S-22 has been included in Foken et al. (2021).
-
(ii)
SM/Table S-23 shows the relative deviation, defined by \(\bigg ({\varrho }_{\text {AV}}^{\text {(TEOS,approx)}} - \) \({\varrho }_{\text {AV}}^{\text {(TEOS)}} \bigg ) /\) \({\varrho }_{\text {AV}}^{\text {(TEOS)}}\) (in percent), of the approximative TEOS-10 values \({\varrho }_{\text {AV}}^{\text {(TEOS,approx)}}\), from the exact (numerical) TEOS-10 values \({\varrho }_{\text {AV}}^{\text {(TEOS)}}\). Relative deviations ≥ 1% are marked in bold style. The maximum of the absolute value of the relative deviation was found to amount ≈ 16% at p = 200hPa, 𝜗 = 60°C, and RH= 100% rh. The table indicates that deviations ≥ 1% are restricted to temperatures of 𝜗≥ 35°C at p = 200hPa, ≥ 45°C at p = 300hPa, ≥ 50°C at p = 400hPa, ≥ 55°C at p = 500hPa, ≥ 60°C at p = 600hPa, and ≥ 60°C at p = 700hPa. Such extreme combinations of temperature and pressure, however, do not occur in Earth’s polytropic troposphere, and are even not expectable in a post-war “nuclear winter” atmosphere with extreme heating at pressure levels p≤ 500hPa (Robock et al. 2007, Fig. 3 therein). Hence, for atmospheric applications the approximative humid-air mass densities differ from the exact ones by less than one percent, and in the major part of the p−T region by not more than a few permille. This accuracy is sufficient for quick-look applications under typical tropospheric conditions. However, for metrological purposes or for applications in numerical models the TEOS-10 SIA library function of the humid-air mass density is recommended to use.
12 Climatological implications of real-gas effects in the mass density of humid air
Analyzing the role of water vapor in the energy balance of the climate system, Feistel and Hellmuth (2020a, see references therein)Footnote 1 estimated the heat flux excess required to increase the global temperature by ΔT = 0.5K over a period of Δt = 30yr corresponding to the observed recent global warming. The authors considered a tropospheric air column extending from the Earth surface at z = z0 until the tropopause at z = zT with air-mass density ϱ and specific isobaric heat capacity cp. The rate of temperature change of this air column originates from the divergence of the diabatic heat flux and is given by the first law:
Here, \(H_{\mathrm {D}}^{\prime }\) denotes the diabatic heat flux (in unit of W m− 2). Counting the heat flux positive in upward direction (positive z-coordinate), the temperature of the air column increases if the heat flux decreases in upward direction. By virtue of the mean-value theorem for definite integrals one can determine the vertically averaged warming rate of the air column (indicated by the overbar) by integration of Eq. (51) from z = z0 to z = zT:
Here, Δz = zT − z0 is the vertical thickness of the air column. Without loss of generality we adopt the following approximation for the mean warming rate:
Therewith one arrives at the following relation:
Adopting \(\overline {c_{\mathrm {p}}}=10^{3} \text {J kg}^{-1} \text {K}^{-1}\), \(\overline {{\varrho }}=1 \text {kg m}^{-3}\), z0 = 0m, zT = 103m (height of the peplopause) or zT = 104m (height of the tropopause), one obtains:
If we interprete \(\overline {{{\varDelta }} T/{{\varDelta }} t}\) as the global-warming signal, then \(H_{\mathrm {D}}^{\prime }(z_{0})-H_{\mathrm {D}}^{\prime }(z_{\mathrm {T}})\) is the difference of the causative excess values of the heat fluxes at the lower and upper boundaries of the atmospheric layer with thickness Δz. A positive value of this difference corresponds to a net warming of this layer, and a negative value to a net cooling. In other words, a perturbation of the energy balance of an atmospheric layer of Δz = 104m by a heat-flux excess of only 5mW m− 2 is sufficient to cause a warming of this layer by ΔT = 0.5K over a period of Δt = 30yr. Feistel and Hellmuth (2020a) showed that the uncertainty of the latent-heat flux originating alone from the uncertainty in the measured relative humidity amounts about 3.6W m− 2 on a global scale. Those authors further argued that the global warming of an air column by a hypothetical excess value of the latent heat flux in the order of \(H_{\mathrm {L}}^{\prime }(z_{0})=5 \text {mW m}^{-2}\) would be already caused by a decrease of the mean relative humidity of only Δ RH ≈− 0.001% rh.
In a similar way we can estimate the real-gas effect of humid air on the heat flux. Representing the sensible heat flux in the form \(H_{\mathrm {S}}(z_{0}) = \overline {c_{\mathrm {p}}} \overline {{\varrho }} \overline {w^{\prime } T^{\prime }}\) with \(\overline {w^{\prime } T^{\prime }}\) denoting the spatio-temporally averaged correlation product of vertical velocity and temperature fluctuations (kinematic heat flux), the relative uncertainty of the heat flux originating from uncertainties in the mass density is given by \({{\varDelta }} H_{\mathrm {S}}(z_{0}) / H_{\mathrm {S}}(z_{0}) \approx {{\varDelta }} \overline {{\varrho }} / \overline {{\varrho }}\). Taking for the real-gas effect in humid air a value of \({{\varDelta }} \overline {{\varrho }} / \overline {{\varrho }} \approx 0.05 \%\) according to Table 4, and adopting \(H_{\mathrm {S}}(z_{0}) \approx 17 \text {W m}^{-2}\) (Trenberth et al. 2009) on a global scale, one obtains \({{\varDelta }} H_{\mathrm {S}}(z_{0}) \approx 8.5 \text {mW m}^{-2}\). Analogously, representing the latent heat flux in the form \(H_{\mathrm {L}}(z_{0}) = \overline {L_{\mathrm {V}}} \overline {{\varrho }} \overline {w^{\prime } q^{\prime }}\) with LV denoting the specific enthalpy of evaporation and \(\overline {w^{\prime } q^{\prime }}\) the spatio-temporally averaged correlation product of vertical velocity and specific humidity fluctuations (kinematic humidity flux), and adopting \(H_{\mathrm {L}}(z_{0}) \approx 80 \text {W m}^{-2}\) (Trenberth et al. 2009) on the global scale, one arrives at \({{\varDelta }} H_{\mathrm {L}}(z_{0}) \approx 40 \text {mW m}^{-2}\).
Although the sensitivity of both the sensible and latent heat fluxes against real-gas effects is extremely small, the tiny bias in the global energy balance caused by real-gas effects in humid air is already large enough to result in a remarkable global warming signal. For this reason real-gas effects deserve consideration in the long-term and large-scale integration of the partial differential equations describing the conservation laws of heat, momentum, and mass underlying climate modelling. This analysis shows that the relevance of real-gas effects depends on the scale and question of interest, which supports the argumentation in Feistel and Hellmuth (2020a).
13 Conclusions
We have analyzed the deviations of the WMO-2014, CIPM-2007, and TEOS-10 formulations of the humid-air mass density from the mass density derived on base of the classical look-up tables presented in Herbert (1987, Table 13-15 therein) (LB-1987). To circumvent the interpolation of the humid-air mass density in its three indepedent variables p, T, and RH from the LB-1987 look-up tables, at first the full analytical form of the LB-1987 approach was recovered from different sources. Note, however, that no conversion between the different historical temperature scales was applied for the LB-1987 formulation. At second, the real-gas effects under atmospheric conditions were quantified. It appeared that under tropospheric conditions these effects are very small with mass densities deviating from the ideal-gas limit by not more than 0.1%. However, in highly accurate hygrometrological applications, which are sensitive to the choice of the temperature scale, real-gas effects should be considered. The deviations of the ITS-90-based WMO-2014, CIPM-2007, and TEOS-10 formulations from the IPTS-68-based LB-1987 reference formulation over a pressure and temperature range corresponding to summerly low-tropospheric condition do not exceed 0.01%. For the WMO-2014 and TEOS-10 formulations over the extended range of tropospheric conditions these deviations do not exceed 0.2% with the maximum occurring for the TEOS-10 formulation at p = 200hPa (tropopause pressure), 𝜗 = 60°C (temperature of a heated skin layer), and RH= 100% rh. The maximum relative deviation of the WMO-2014-based formulation from the TEOS-10 formulation was found to amount − 0.27%, occurring at p = 200hPa, 𝜗 = 60°C, and RH = 100% rh. However, the combinations of p, T, and RH values at which these maximum deviations occur are not expectable under tropospheric conditions.
In view of the smallness of these deviations the choice of the formulation depends primarily on the question of interest and is not crucial for most applications. One should note, however, that the highly accurate CIPM-2007 formulation is valid only for low-tropospheric conditions in a very limited temperature range. The closeness of the WMO-2014 and TEOS-10 formulations throughout the range of tropospheric pressures and temperatures supports the applicability of the advanced seawater standard TEOS-10, developed for oceanic use, also for meteorological purposes. The TEOS-10 humid-air mass density is determined in a thermodynamically rigorous way from the Helmholtz potential of humid air by numerical iteration of a transcendental equation. A FORTRAN subroutine from the TEOS-10 SIA program library provides a convenient means to perform numerical calculations. The TEOS-10 SIA program library is freely available from the TEOS-10 website.
For quick-look estimations of the humid-air mass density at tropospheric conditions we have presented in SM/Table S-22 a TEOS-10 based, approximative look-up table of the virtual temperature increment of saturated humid air together with the virial-corrected dry-air mass density. The approximation proposed here is sufficiently accurate for quick-look purposes with the humid-air mass density deviating by less then one percent from exact calculations for meteorologically relevant combinations of pressure and temperature. This look-up table is part of the handbook of Foken et al. (2021). The analysis of the sensitivity of the compressibility factor of humid air against different formulations of the virial coefficients is subject of ongoing work.
Notes
The English translation of this publication is given by Feistel and Hellmuth (2020b).
For the sake of completeness we mention two further TEOS-10 generating thermodynamic potentials, that are the specific Helmholtz energy, fA(T,ϱA), of dry air (as a function of the ITS-90 temperature T, and the mass density of dry air, ϱA) (Lemmon et al. 2000), and the specific Gibbs energy of seasalt dissolved in water (Feistel 2003, 2008, and IAPWS R13-08 2008).
In the original paper of Goff and Gratch (1946, Eq. (20) therein) there is some confusion with the physical units. The expression \(A_{\text {WW}}^{\prime }\) is given in units of ft3/lb, that of \(A_{\text {WWW}}^{\prime }\) in units of ft5/lb2, and temperature in units of °R. Thus, the product \(p A_{\text {WW}}^{\prime }\) should have the unit Jkg− 1 instead of ft as announced in the paper. If \(p A_{\text {WW}}^{\prime }\), however, has the unit of a mass-specific energy (J kg− 1), than the product RT must have the same physical unit with R being the specific gas constant of humid air. However, in the paper RT is given in units of a molar energy (cm3atm/mole, corresponding to Jmol− 1). If, as indicated in the paper, the product \(p A_{\text {WW}}^{\prime }\) has the unit ft and RT the unit cm3atm/mole, an incompatibility in Goff and Gratch (1946, Eq. (2) therein) occurs, because in the difference \((RT{-}A_{\text {ww}}^{\prime })\) subtrahend and minuend have different physical units. Therefore, for application the user should consequently switch to the SI system of units.
References
Alberty RA (2001) Use of Legendre transforms in chemical thermodynamics (IUPAC Technical Report). Pure Appl Chem 73 (8):1349. https://doi.org/10.1351/pac20017308134
Alexander MA, Schubert SD (1990) Regional earth-atmosphere energy balance estimates based on assimilations with a GCM. J. Climate 3:15. https://journals.ametsoc.org/view/journals/clim/3/1/1520-0442_1990_003_0015_reaebe_2_0_co_2.xml?tab_body=pdf
BIPM (2019) The International System of Units (SI). Bureau International des Poids et Mesures, Edite par le BIPM, Pavillon de Breteuil, F-92312 Sevres Cedex, France 9th edn
Baur F (1970) Meteorologisches Taschenbuch. Begründet von Franz Linke. Neue Ausgabe. II. Band (Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig)
Bögel W (1977) Neue Näherungsgleichungen für den Sättigungsdruck des Wasserdampfes und für die in der Meteorologie gebräuchlichen Luftfeuchte-Parameter (DFVLR-Inst. Phys. Atm., Oberpfaffenhofen, DLR-FB 77-52, 158)
Bohren CF, Albrecht BA (1998) Atmospheric thermodynamics. Oxford University Press, New York
Buck AL (1981) New equations for computing vapor pressure and enhancement factor. J Appl Meteorol 20(12):1527. https://journals.ametsoc.org/view/journals/apme/20/12/1520-0450_1981_020_1527_nefcvp_2_0_co_2.xml
Cotton WR, Anthes RA (1989) Storm and cloud dynamics. Academic Press, Inc, San Diego
Feistel R (2003) A new extended Gibbs thermodynamic potential of seawater. Prog Oceanogr 58(1):43. https://doi.org/10.1016/S0079-6611(03)00088-0
Feistel R (2008) A Gibbs function for seawater thermodynamics for − 6 to 80°C and salinity up to 120 g kg− 1. Deep Sea Research Part I: Oceanographic Research Papers. Deep-Sea Research 55(12):1639. https://doi.org/10.1016/j.dsr.2008.07.004
Feistel R (2012) TEOS-10: a new international oceanographic standard for seawater, ice, fluid water, and humid air. Int J Thermophys 33:1335. https://doi.org/10.1007/s10765-010-0901-y
Feistel R (2015) Salinity and relative humidity: climatological relevance and metrological needs. ACTA IMEKO 4(4):57. file:///Users/olaf/Downloads/216-1990-1-PB.pdf
Feistel R (2018) Thermodynamic properties of seawater, ice and humid air: TEOS-10, before and beyond. Ocean Sci 14:471. https://doi.org/10.5194/os-14-471-2018
Feistel R (2019) Defining relative humidity in terms of water activity. Part 2: relations to osmotic pressures. Metrologia 56(1):015015. https://doi.org/10.1088/1681-7575/aaf446
Feistel R, Hellmuth O (2020a) Zur Rolle des Wassers in der Energiebilanz des Klimasystems. Sitzungsberichte der Leibniz-Sozietat der Wissenschaften 144:51. https://leibnizsozietaet.de/wp-content/uploads/2021/03/Gesamtdatei-SB-144-2020.pdf
Feistel R, Hellmuth O (2020b) On the role of water in the energy balance of the climate system. ResearchGate:https://www.researchgate.net/publication/339289982_On_the_Role_of_Water_in_the_Energy_Balance_of_the_Climate_System
Feistel R, Lovell-Smith JW (2017) Defining relative humidity in terms of water activity. Part 1: definition. Metrologia 54 (4):566. http://stacks.iop.org/0026-1394/54/i=4/a=566
Feistel R, Lovell-Smith J, Hellmuth O (2015a) Virial approximation of the TEOS-10 equation for the fugacity of water in humid air. Int J Thermophys 36:44. https://doi.org/10.1007/s10765-014-1784-0
Feistel R, Lovell-Smith J, Hellmuth O (2015b) Erratum to: virial approximation of the TEOS-10 equation for the fugacity of water in humid air. Int J Thermophys 36:44. https://doi.org/10.1007/s10765-014-1827-6
Feistel R, Wagner W (2006) A new equation of state for H2O ice Ih. J Phys Chem Ref Data 35:1021. https://doi.org/10.1063/1.2183324
Feistel R, Wielgosz R, Bell SA, Camões MF, Cooper JR, Dexter P, Dickson AG, Fisicaro P, Harvey AH, Heinonen M, Hellmuth O, Kretzschmar H, Lovell-Smith JW, McDougall TJ, Pawlowicz R, Ridout P, Seitz S, Spitzer P, Stoica D, Wolf H (2016a) Metrological challenges for measurements of key climatological observables: oceanic salinity and pH, and atmospheric humidity. Part 1: overview. Metrologia 53(1):R1. http://stacks.iop.org/0026-1394/53/i=1/a=R1
Feistel R, Wielgosz R, Bell SA, Camões MF, Cooper JR, Dexter P, Dickson AG, Fisicaro P, Harvey AH, Heinonen M, Hellmuth O, Kretzschmar H, Lovell-Smith JW, McDougall TJ, Pawlowicz R, Ridout P, Seitz S, Spitzer P, Stoica D, Wolf H (2016b) Digital supplement to Metrological challenges for measurements of key climatological observables: oceanic salinity and pH, and atmospheric humidity. Part 1: overview. Metrologia 53 (1):R1. https://iopscience.iop.org/article/10.1088/0026-1394/53/1/R1/data, https://cfn-live-content-bucket-iop-org.s3.amazonaws.com/journals/0026-1394/53/1/R1/1/MET517141suppdata.pdf?AWSAccessKeyId=AKIAYDKQL6LTV7YY2HIK&Expires=1630407437&Signature=euN4LAWLcB7nlwLqRUlbp1O1zVw%3D
Feistel R, Wright DG, Kretzschmar H-J, Hagen E, Herrmann S, Span R (2010a) Thermodynamic properties of sea air. Ocean Sci 6:91. http://www.ocean-sci.net/6/91/2010/
Feistel R, Wright DG, Jackett DR, Miyagawa K, Reissmann JH, Wagner W, Overhoff U, Guder C, Feistel A, Marion GM (2010b) Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 1: Background and equations. Ocean Sci 6:633. https://doi.org/10.5194/os-6-633-2010. http://www.ocean-sci.net/6/633/2010/
Fleagle RG, Businger JA (1980) An introduction to atmospheric physics, 2nd edn. Academic Press, Inc, Orlando
Foken T (2018) Nachruf Prof. Dr. habil. Dietrich Sonntag. Mitteilungen der Deutschen Meteorologischen Gesellschaft (DMG). 1:29
Foken T, Hellmuth O, Huwe B, Sonntag D (2021) Physical quantities (Chapter 5). In: Foken, T (ed) Springer handbook of atmospheric measurements. Springer International Publishing. https://doi.org/10.1007/978-3-030-52171-4
Goff JA (1949a) Final report of the working subcommittee of the International Joint Committee on Psychrometric Data. Transactions of the ASME. November 903
Goff JA (1949b) Standardization of thermodynamic properties of moist air. Final report of working subcommittee, International Joint Committee on Psychrometric Data. Transactions American Society of Heating and Ventilating Engineers 1375:459–484
Goff JA (1949c) Standardization of thermodynamic properties of moist air. Final report of working subcommittee, International Joint Committee on Psychrometric Data. Heating, piping & air conditioning. ASHVE J Sect 55:118
Goff JA, Gratch S (1945) Thermodynamic properties of moist air. Transactions American Society of Heating and Ventilating Engineers (ASHVE). Nr 51 (1270):125
Goff JA, Gratch S (1946) Low pressure properties of water from –160 to 212 F. Transactions American Society of Heating and Ventilating Engineers (ASHVE). Nr 52(1286):95
Guggenheim EA (1950) Thermodynamics. An advanced treatment for chemists and physicists. North-Holland Publishing Company, Amsterdam
Guyot A (1852) A Collection of Meteorological Tables with other Tables useful in Practical Meteorology Prepared by Order of the Smithsonian Institution (Smithsonian Institution, Washington. Reprint of Forgotten Books 2016 FB & c Ltd
Harvey AH, Huang PH (2007) First-principles calculation of the air-water second virial coefficient. Int J Thermophys 28:556. https://doi.org/10.1007/s10765-007-0197-8
Hellmuth O, Feistel R, Foken T (2021) Supplementary material to “Intercomparison of different state-of-the-art formulations of the mass density of humid air. Table values”. Bull. of Atmos. Sci. & Technol. https://doi.org/10.1007/s42865-021-00036-7
Herbert F (1987) Meteorology. Subvolume A: Thermodynamical and Dynamical Structures of the Global Atmosphere (G Fischer, F Herbert, R A Madden, M Schlegel, P Speth). In: Fischer G (ed) Landolt-Börnstein – Numerical Data and Functional Relationships in Science and Technology. New Series. Editors in Chief: K-H Hellwege, O Madelung. Group V: Geophysics and Space Research. https://doi.org/10.1007/b32395, ISBN: 3-540-16610-6, vol 4. Springer, Berlin, p 491
Hyland RW, Wexler A (1983a) Formulations for the thermodynamic properties of the saturated phases of H2O from 173.15 K to 473.15 K. Trans Am Soc Heat Refrig Air Cond Eng 89:500
Hyland RW, Wexler A (1983b) Formulations for the thermodynamic properties of dry air from 173.15 K to 473.15 K, and of saturated moist air from 173.15 K to 372.15 K, at pressures to 5 MPa. ASHRAE Transact. (RP-216) 89:520
IAPWS G5-01 (2016) Guideline on the use of fundamental physical constants and basic constants of water. Tech. rep., The International Association for the Properties of Water and Steam, Gaithersburg, Maryland, United States of America, September 2001. http://www.iapws.org
IAPWS G9-12 (2012) Guideline on a low-temperature extension of the IAPWS-95 formulation for water vapor. Tech. rep., The International Association for the Properties of Water and Steam, Boulder, Colorado, USA, October 2012. http://www.iapws.org
IAPWS R10-06 (2009) Revised release on the equation of state 2006 for H2O ice Ih. Tech. rep., The International Association for the Properties of Water and Steam, Doorwerth, The Netherlands, September 2009. http://www.iapws.org
IAPWS R13-08 (2008) Release on the IAPWS formulation 2008 for the thermodynamic properties of seawater. Tech. rep., The International Association for the Properties of Water and Steam, Berlin, Germany, September 2008. http://www.iapws.org
IAPWS R6-95 (2016) Revised release on the IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. Tech. rep., The International Association for the Properties of Water and Steam, Dresden, Germany, September 2016. http://www.iapws.org
IAPWS SR7-09 (2009) Revised release on the equation of state 2006 for H2O ice ih. Tech. rep., The International Association for the Properties of Water and Steam, Doorwerth, The Netherlands, September 2009. http://www.iapws.org
IOC, SCOR, IAPSO (2010) The international thermodynamic equation of seawater – 2010: Calculation and use of thermodynamic properties. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English), 196 pp., Paris 2010. http://www.teos-10.org
Iribarne JV, Godson WL (1981) Atmospheric thermodynamics. Geophysics and Astrophysics Monographs, vol. 6, Second revised edition, D. Reidel Publishing Company
Jacobson MZ (2005) Fundamentals of atmospheric modeling, 2nd edn. Cambridge University Press, Cambridge
Kluge G, Neugebauer G (1994) Grundlagen der Thermodynamik. Spektrum Akademischer Verlag, Heidelberg. ISBN 3-86025-301-8
Lemmon EW, Jacobsen RT, Penoncello SG, Friend DG (2000) Thermodynamic properties of air and mixtures of nitrogen, argon, and oxygen from 60 to 2000 K at pressures to 2000 MPa. J Phys Chem Ref Data 29:331. https://doi.org/10.1063/1.1285884
Liljequist GH, Cehak K (1984) Allgemeine Meteorologie, 3rd edn. Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig
Lovell-Smith J (2006) On correlation in the water vapour pressure formulations. Metrologia 43:556. https://doi.org/10.1088/0026-1394/43/6/011.
Lovell-Smith J (2007) An expression for the uncertainty in the water vapour pressure enhancement factor for moist air. Metrologia 44(6):L49. https://doi.org/10.1088/0026-1394/44/6/N01.
Lovell-Smith J (2009) The propagation of uncertainty for humidity calculations. Metrologia 46(6):607. https://doi.org/10.1088/0026-1394/46/6/001.
Lovell-Smith J, Feistel R, Harvey AH, Hellmuth O, Bell SA, Heinonen M, Cooper JR (2016) Metrological challenges for measurements of key climatological observables. Part 4: atmospheric relative humidity. Metrologia 53(1):R40. https://iopscience.iop.org/article/10.1088/0026-1394/53/1/R40
Mohr PJ, Taylor BN (2005) CODATA recommended values of the fundamental physical constants: 2002. Rev Mod Phys 77:1. https://doi.org/10.1103/RevModPhys.77.1
Mölders N., Kramm G (2014) Lectures in meteorology. Springer International Publishing, Berlin. https://doi.org/10.1007/978-3-319-02144-7
Picard A, Davis RS, Gläser M., Fujii K (2008) Revised formula for the density of moist air (CIPM-2007). Metrologia 45(2):149. https://doi.org/10.1088/0026-1394/45/2/004
Pielke RA (1984) Mesoscale meteorological modeling. Academic Press, Harcourt Brace Jovanovich Publishers, Orlando. Publishers, Orlando
Prausnitz JM, Lichtenthaler RN, de Azevedo EG (1999) Molecular thermodynamics of fluid-phase equilibria. Prentice Hall PTR. Upper Saddle River, New Jersey
Pruppacher HR, Klett JD (2004) Microphysics of clouds and precipitation. Kluwer Academic Publishers, Dordrecht/Boston/London
Robock A, Oman L, Stenchikov GL (2007) Nuclear winter revisited with a modern climate model and current nuclear arsenals: Still catastrophic consequences. J. Geophys. Res. 112:D13107. https://doi.org/10.1029/2006JD008235
Salby ML (2012) Physics of the atmosphere and climate, 2nd edn. Cambridge University Press, Cambridge
SMT (1951) Smithsonian meteorological tables, 6th edition. Tech. Rep. Smithsonian Institution, Washington
Sonntag D (1989) WMO Assmann aspiration psychrometer intercomparison. Instruments and observing methods. Report No.34 WMO/TD-No. 289, 177 Tech. rep. Geneva
Sonntag D (1990) Important new values of the physical constants of 1986, vapour pressure formulations based on the ITS-90 and psychrometer formulae. Z Meteorol 5:340
Sonntag D, Zeitschrift NF (1994) Advancements in the field of hygrometry. Meteorol. Zeitschrift, N.F. 3:51
Teleszewski TJ, Gajewski A (2020) The latest method for surface tension determination: experimental validation. Energies 13:14. https://doi.org/10.3390/en13143629. https://www.mdpi.com/1996-1073/13/14/3629
Trenberth KE, Fasullo JT, Kiehl J (2009) Earth’s global energy budget. Bull Amer Meteorol Soc March:311. https://doi.org/10.1175/2008BAMS2634.1
Trenberth KE, Hurrell JW, Solomon A (1995) Conservation of mass in three dimensions in global analyses. J Climate 8:692. https://doi.org/10.1175/1520-0442(1995)00<0692:COMITD>2.0.CO;2
Wagner W, Pruß A (2002) The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J Phys Chem Ref Data 31:387. https://doi.org/10.1063/1.1461829
WMO (1966) International meteorological tables. Report WMO-No. 188, TP 94, updated 1973. Edited by S Letestu. Tech. rep., World Meteorological Organization. Geneva, Switzerland
WMO (1968) International meteorological tables. Report WMO-No. 188 TP 94, Edited by S Letestu. Tech. rep., World Meteorological Organization, Geneva, Switzerland
WMO (2014) Guide to meteorological instruments and methods of observation. World Meteorological Organization, WMO-No. 8, 2014 edition, updated in 2017. Geneva, Switzerland. https://library.wmo.int/doc_num.php?explnum_id=4147
Wieser ME (2006) Atomic weights of the elements 2005 (IUPAC Technical Report). Pure Appl Chem 78:2051
Wright DG, Feistel R, Reissmann JH, Miyagawa K, Jackett DR, Wagner W, Overhoff U, Guder C, Feistel A, Marion GM (2010) Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 2: The library routines. Ocean Sci 6:695. https://doi.org/10.5194/os-6-695-2010
Zdunkowski W, Bott A (2004) Thermodynamics of the atmosphere. a course in theoretical meteorology. Cambridge University Press, Cambridge
Acknowledgements
The authors are very grateful to the two anonymous referees for their very careful and detailed reviews, their specific comments and instructive suggestions to improve the manuscript, and their fair evaluation. The contribution of O. Hellmuth was provided within the framework of the research theme 1 “Aerosols: Process studies at small temporal and spatial scales” of Leibniz Institute for Tropospheric Research (TROPOS), Leipzig. This work contributes to the task of the IAPWS/SCOR/IAPSO Joint Committee on the Properties of Seawater (JCS).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Supplementary information
The online version contains supplementary material available at https://doi.org/10.1007/s42865-021-00036-7.
Author contribution
O. Hellmuth executed the calculations, evaluated the data, and prepared the manuscript draft; R. Feistel prepared the TEOS-10 part including Appendices A and B, contributed to the data evaluation, and revised the manuscript; T. Foken gave the inspiration for the manuscript and for the inclusion of the WMO-2014 formulation, contributed to the data evaluation, and revised the manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is dedicated to the memory of Prof. Dr. habil. Dietrich Sonntag (23 June 1927–1 January 2018), who contributed so much to all aspects of hygrometry with special predilection for the highly accurate determination of hygrometric properties and table values for the meteorological practice (see epitaph by Foken 2018).
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix 1. Thermodynamic potentials of humid air
1.1 A1.1 Basic remarks
In the description of geophysical thermodynamic properties, the International Thermodynamic Equation of Seawater (TEOS-10) is the first international standard that is rigorously based on thermodynamic potentials in an axiomatic way (Feistel et al. 2016a, b; Feistel 2018). All required properties can be defined mathematically in terms of only three empirical functions, plus some general constants such as molar masses or the gas constant. This approach permits an analysis of internal relations between quantities that otherwise are often formulated from apparently independent experimental data. Here we express several fundamental quantities of atmospheric physics in terms of the TEOS-10 thermodynamic potentials.
1.2 A1.2 General thermodynamic relations
Thermodynamic properties of humid air, including its saturation states, can be derived from three analytical empirical functions, the so-called thermodynamic potentials of humid air, of liquid water and of ambient ice Ih. In the framework of TEOS-10, these functionsFootnote 2 are, respectively,
-
(i) the specific Helmholtz energy, fAV(A,T,ϱAV), of humid air as a function of the dry-air mass fraction, A, the temperature, T, on the International Temperature Scale 1990 (ITS-90), and the mass density, ϱAV;
-
(ii) the specific Helmholtz energy, fW(T,ϱW), of liquid water as a function of the ITS-90 temperature, T, and the mass density of liquid water, ϱW (Wagner and Pruß 2002; IAPWS R6-95 2016) (known as “IAPWS-95”);
-
(iii) the specific Gibbs energy, gIh(T,p), of hexagonal ice I as a function of the ITS-90 temperature T, and the pressure, p (Feistel and Wagner 2006; IAPWS R10-06 2009).
In combination with air–water cross-virial coefficients (see Hyland and Wexler 1983a, 1983a, Harvey and Huang 2007, Feistel et al. 2010a) this set of thermodynamic potentials is used as the primary standard for pure water (liquid, vapor, and solid), seawater and humid air from which all other properties are derived by mathematical operations, i.e., without the need for additional empirical functions. For meteorological applications, the TEOS-10 Helmholtz function of humid air, fAV, may be approximated with sufficient accuracy by virial coefficients (Feistel et al. 2015a, Eq. (3) and references therein):
The partial mass densities of the vapor and the air, respectively, are ϱV = (1 − A)ϱAV and ϱA = AϱAV, their related molar densities are \(\widetilde {{\varrho }}_{\mathrm {V}}={\varrho }_{\mathrm {V}}/M_{\mathrm {W}}\) and \(\widetilde {{\varrho }}_{\mathrm {A}}={\varrho }_{\mathrm {A}}/M_{\mathrm {A}}\), their molar masses are MW and MA, their specific gas constants are RW = R/MW and RA = R/MA, and R is the molar gas constant. According to Eq. (A1.1), the function \(f_{\text {AV}} \left (A,T,{\varrho }_{\text {AV}} \right )\) is composed of a dry-air part given by the specific Helmholtz energy for dry air, \(f_{\mathrm {A}} \left (T,{\varrho }_{\mathrm {A}} \right )\) Lemmon et al. (2000), of a water-vapor part given by the specific Helmholtz energy for water vapor, \(f_{\mathrm {V}} \left (T,{\varrho }_{\mathrm {V}} \right )\), which is defined by the thermal equation of state of fluid water (Wagner and Pruß 2002, IAPWS-95), and of a part describing the contribution of air–vapor interactions to the mixture properties, \(f_{\text {mix}} \left (A,T,{\varrho }_{\text {AV}} \right )\) (Feistel et al. 2015a, Eqs. (14), (15), (16), and references therein):
The quantity \(\widetilde {{\varrho }}_{0}\) is an arbitrary reference molar density, such as \(\widetilde {{\varrho }}_{0}=1 \text {mol m}^{-3}\), introduced only to render the argument of the logarithm unitless. The functions fV,0(T) and fA,0(T) are relatively complicated mathematical expressions related to ideal-gas heat capacities; these functions are not relevant for the following derivations, and explicitly reporting them is refrained from here.
In Eqs. (A1.2)–(A1.4), BWW(T) and CWWW(T) denote the second and third molar virial coefficients (VCs) for water–water interactions, BAA(T) and CAAA(T) the second and third molar virial coefficients for air–air interactions, and BAW(T), CAWW(T), CAAW(T) the second and third molar cross-virial coefficients for air–water interactions. The second virial coefficients are given in units of the molar volume (m3mol− 1), and the third ones in units of the square of the molar volume (m6mol− 2). These seven functions are mutually independent and are sufficient to describe all thermodynamic real-gas corrections of humid air. It is the aim of this Appendix to provide rigorous relations for quantities of meteorological interest in terms of these seven VCs. Various empirical formulas for these VCs are available from the scientific literature; in Appendix 2 we shall focus on only those which are related the selected meteorological standard equations.
Expressing Eq. (A1.1) in terms of these seven VCs, the Helmholtz function of humid air reads:
In Eq. (A1.5) these seven VCs appear in two regular combinations of the so-called mixture virial coefficients B(xV,T) and C(xV,T) (Guggenheim 1950; Prausnitz et al. 1999, pp. 133–134, Eqs. (5.20), (5.22) therein):
In Eqs. (A1.6) and (A1.7) the quantity xV is the mole fraction of water vapor in humid air,
MAV is the mean molar mass of the binary gas mixture “humid air”,
and
is an abbreviation. Thermodynamic potentials may be mathematically transformed in various ways to be expressed in suitable independent variables (Alberty 2001). To replace the density argument of the Helmholtz function f(T,ϱ) by the more convenient pressure, by virtue of
a Gibbs function g(T,p) may be employed, which is obtained by the so-called Legendre transformation:
The virial equation for the pressure of humid air is obtained from the density derivative, Eq. (A1.11), of the Helmholtz function, Eq. (A1.5):
In TEOS-10, the Gibbs function of liquid water, gW(T,p), is computed numerically from fW(T,ϱW), but for low-pressure conditions an analytical version of gW is available (Feistel 2003; IAPWS SR7-09 2009). The virial equation for the Gibbs function of humid air related to the Helmholtz function, Eq. (A1.1), takes the form
The virial equation for the mass density of humid air is obtained from gAV(A,T,p) via
Introducing the variable y = p/(RT), Eq. (A1.13) can be brought into the following form:
Analogously, Eq. (A1.15) assumes the following form:
Equating the pressures defined by Eqs. (A1.16) and (A1.17) yields:
Inserting y from Eq. (A1.16) into the right-hand side of Eq. (A1.18), one arrives at the following relation:
The satisfaction of the last relation in Eq. (A1.19) requires the fulfillment of the following relations between the coefficients of the pressure expansion, Eq. (A1.15), and the original VCs introduced by Eq. (A1.13):
The inverse relations read:
Also, from Eq. (A1.12), g = f + p/ϱ, it follows that
By virtue of Eq. (A1.20) the virial equation for the Gibbs function of humid air, Eq. (A1.14), can be expressed in terms of the original VCs:
Analogously, the virial equation for the mass density of humid air, Eq. (A1.15), can be rewritten as follows:
1.3 A1.3 Virial form of thermodynamic properties
1.3.1 A1.3.1 Basic remarks
Virial coefficients are basic thermodynamic quantities which contain the full information about the real-gas behavior of a vapor or a vapor mixture. These coefficients represent a complete, self-consistent, and independent description of real gases, while thermodynamic derivables given in form of empirical or semiempirical functions do neither fulfill the criterion of independency from each other, nor the criterion of completeness. In other words, it is impossible to provide separate empirical formulae for such derivables, which do not lead to discrepancies in the corresponding VCs retrieved from these formulae.
The thermodynamic equilibrium conditions given by Eqs. (9) and (10) allow the determination of the mole fraction of water vapor in saturated humid air, \(x_{\text {V,sat}}^{\text {(c)}}\), and saturation pressure of water vapor, \(e_{\text {sat}}^{\text {(c)}}\), respectively. In TEOS-10, the chemical potentials of liquid water and ice, μW(T,p) and μIh(T,p), are available as functions of temperature and pressure. Furthermore, in Feistel et al. (2015a, 2015a) also virial approximations of the TEOS-10 equations for the fugacity and the chemical potential of water vapor in humid, \(\mu _{\mathrm {W}}^{\text {AV}}(x_{\mathrm {V}},T,p)\), are derived. This preparatory effort suggests the possibility of expressing \(x_{\text {V,sat}}^{\text {(c)}}\) and \(e_{\text {sat}}^{\text {(c)}}\) in terms of VCs. The derivation of virial representations for these two quantities, however, is a nontrivial and pending task, which is beyond the scope of the present study. The same holds true for the enhancement factor, f(c)(T,p), defined by Eq. (11). Therefore, below we restrict our consideration to the derivation of the virial forms of the compressibility coefficient and the virtual temperature, which can be obtained in a more straightforward manner.
1.3.2 A1.3.2 Virial form of the compressibility coefficient
The compressibility coefficient of humid air, ZAV, is defined by Eq. (14) as
By virtue of Eq. (A1.13), ZAV can be expressed as a series expansion with respect to the molar density:
Analogously, by virtue of Eqs. (A1.15) and (A1.24), ZAV can be expressed as a series expansion with respect to pressure:
These equations permit the a posteriori derivation of associated VCs from several published empirical functions ZAV. Such VCs, in turn, permit comparison with VCs derived from other empirical formulas, such as for the density. The special case of the compressibility factor for dry air can be recovered from Eqs. (A1.26) and (A1.27) for xV = 0:
1.3.3 A1.3.3 Virial form of the virtual temperature
The general expression of the virtual temperature, Tv, is defined by Eq. (17):
For meteorological applications this temperature is typically evaluated as function of the pressure. By virtue of ZAV(p) from Eq. (A1.27) and ZA(p) from Eq. (A1.29) the virial form of the virtual temperature reads:
Empirical equations available for Tv permit the estimation of associated VCs by means of Eqs. (A1.27)–(A1.28) or (A1.31), respectively, or by suitable low-pressure series expansions of those equations.
Appendix 2. Compressibility factor employed in the LB-1987 approach
1.1 A2.1 Compressibility factor of nitrogen
As a first guess, Herbert (1987, p. 74 therein) approximated the compressibility factor of humid air, ZAV, by the one of nitrogen, serving in turn as proxy of dry air. The corresponding virial form of ZAV is given by the following relation:
The coefficients \(B^{\prime }_{\mathrm {k}}(T)\) are presented in Table 8. Equation (A2.1) is equivalent to the textbook-like form, Eq. (A1.27), with the pressure-expanded VCs b, c, and d determined by the following transformations:
By virtue of Eq. (A1.21), the density-expanded VCs read
For temperatures in the interval 200K<T< 300K the VCs \(B^{\prime }_{1}\), \(B^{\prime }_{2}\), and \(B^{\prime }_{3}\) in Table 8 must be interpolated. As the VCs vary by more than one order of magnitude over this range and as the corresponding temperature coefficients differ by their signs (\(\mathrm {d}B^{\prime }_{1}/\mathrm {d}T>0\), \(\mathrm {d}B^{\prime }_{2}/\mathrm {d}T>0\), and \(\mathrm {d}B^{\prime }_{3}/\mathrm {d}T<0\)) it would be desirable to have physical a priori information for the specification of the appropriate interpolation. However, due to lack of such guiding information in Herbert (1987, p. 74 therein) as a first guess we applied linear interpolation appearing the simplest one. One can at least expect that the uncertainty of such practice is not larger than those originating from linear interpolation of look-up table values. However, the analysis of the sensitivity of \(Z_{\text {N}_{2}}(T,p)\) against the interpolation method for the coefficients \(B^{\prime }_{1}\), \(B^{\prime }_{2}\), and \(B^{\prime }_{3}\) as well as against the application of alternative expressions for the temperature dependence of the VCs is beyond the scope of the present study, but is subject of an ongoing work.
1.2 A2.2 Compressibility factor of humid air
For a refined guess of the compressibility factor, Herbert (1987, Section 2.3.3, Table 15 therein) presented table values of ZAV with reference to WMO (1968). In the source (WMO 1968, Table 4.12.2 therein) in turn, reference is given to SMT (1951, pp. 331–333 and Table 84 therein)Footnote 3, which again relegates to the Goff–Gratch formulation of the thermodynamic properties of air and water vapor as published in Goff and Gratch (1945, 1946), and Goff(1949a)Footnote 4.
The form of ZAV used in SMT (1951, Table 84 therein) can be derived from Goff and Gratch (1945, Eq. (13.8) therein):
Here, xA = 1 − xV denotes the mole fraction of dry air in humid air. By virtue of the definition \(Z_{\text {AV}}=p/(RT \widetilde {{\varrho }}_{\text {AV}})\), Eq. (A2.4) can be rewritten as follows:
Here, \(A_{\text {AA}}^{\prime }\), \(A_{\text {WW}}^{\prime }\), and \(A_{\text {AW}}^{\prime }\) (in units of a molar volume, m3mol− 1) are coefficients, which are related to the second molar virial and cross-virial coefficients of molecular air–air, water–water, and air–water interactions, BAA, BWW, and BAW, respectively, and \(A_{\text {WWW}}^{\prime }\) (in units of m3mol− 1Pa− 1) is related to the third molar VC of interactions between three water molecules, CWWW. As Goff and Gratch (1945, p. 139 therein) did neither had experimental nor theoretical information regarding the triple-interactions coefficients \(A_{\text {AAA}}^{\prime }\), \(A_{\text {AAW}}^{\prime }\), and \(A_{\text {AWW}}^{\prime }\), they were entirely neglected in Eq. (A2.4).
The LB-1987 form of ZAV, Eq. (A2.5), is equivalent to the textbook-like form, Eq. (A1.27),
with the second and third VCs defined by Eqs. (A1.6) and (A1.7),
and the replacements
and
While \(A_{\text {WWW}}^{\prime }\) is given in units of m3mol− 1Pa− 1, the commonly used third VC, CWWW, is given in units of m6mol− 2.
Parameterizations of the virial-like coefficients \(A_{\text {AA}}^{\prime }\), \(A_{\text {WW}}^{\prime }\), \(A_{\text {WWW}}^{\prime }\), and \(A_{\text {AW}}^{\prime }\) used in the LB-1987 formulation are given in Goff and Gratch (1945, Eqs. (2.4), (8.1), (8.2), and (16.2) therein). However, as SMT (1951, pp. 331–333 and Table 84 therein) cited the later publication of Goff (1949a), here the virial-like coefficients were taken from this source. Correspondingly, the second virial-like coefficient of dry air reads (Goff 1949a, Table 3 therein):
For the second and third virial-like coefficients of water vapor, Goff (1949a, Tables 4 and 5 therein) referred to the formulation provided by Goff and Gratch (1946, Eq. (20) therein)Footnote 5:
For the second cross virial-like coefficient of air–water interactions, Goff (1949a, Table 6 therein) referred to the formulation provided by Goff and Gratch (1945, Eq. (16.2) therein):
To avoid spurious misfits outside the declared definition ranges of \(A_{\text {AA}}^{\prime }\), \(A_{\text {AW}}^{\prime }\), \(A_{\text {WW}}^{\prime }\), and \(A_{\text {WWW}}^{\prime }\), the VCs were set to zero beyond the declared temperature intervals (instead of extrapolating the corresponding formulas beyond their definition ranges). Zeroing simultaneously all of the VCs corresponds to idealization of the gas-phase mixture.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hellmuth, O., Feistel, R. & Foken, T. Intercomparison of different state-of-the-art formulations of the mass density of humid air. Bull. of Atmos. Sci.& Technol. 2, 13 (2021). https://doi.org/10.1007/s42865-021-00036-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42865-021-00036-7