1 Introduction

When gamma-rays pass through a material, some photons pass through without interaction, while the remainder is absorbed and scattered by the material. The gamma energy, the atomic number of the materials, and the thickness of the materials all influence the attenuation of gamma radiation through matter [1]. For lower or higher gamma energies, materials with higher atomic numbers produce a more effective shield than those with lower ones [2]. Currently, many polymer matrices that can be used as gamma-ray shields have been focused on and reported by radiation protection researchers, including poly (methyl methacrylate) composites, high-density polyethylene (HDPE), polyvinyl chloride (PVC) polymer, resin polymer composites, silicone rubber, polymer bricks (PolyBiz), and polyester [3,4,5].

Epoxy polymer is one of the most significant thermoset polymers used in composite manufacturing due to the qualities of the entire composite through its strong chemical resistance, high stiffness, superior mechanical strength, flame retardancy, and high electrical strength. Solid epoxy polymer is the output material obtained by the reaction of the curing agent with liquid resin. When an epoxy-based system is exposed to radiation, additional structural changes are noticed in addition to the crosslinking that results from the reaction between the curing agent and epoxy resin. Depending on the exposure amount and raw materials used to make epoxy resin, the color of the resin might change from translucent to yellow and even deteriorate. To ensure excellent radiation stability for matrix elements in composite manufacturing, epoxies are still used. [6, 7]. Increased interactions between the filler and epoxy matrix improve the composite's overall resilience to various destructive forces. Elastomeric/thermoplastic phases can be successfully incorporated, as organic/inorganic particles, into epoxy resins to make improvements.

The incorporation of a filler in a variety of micro-sizes in the composite material improves the composite's properties. The bond between the polymer and the matrix is weakening due to chemical and intermolecular forces. A nanofiller, on the other hand, can be distributed through the polymer matrix at the nanometric scale. Thus, chemical bonding improves the molecular interactions between the matrix and the filler, resulting in further improvements in the mechanical and physical properties of the new polymer nano-composites [8]. The high surface-to-volume ratio of nanofillers affects the change in macromolecular status around nanoparticles. The addition of nanofiller improves polymer properties such as elasticity and strength, as well as heat and barrier resistance, gas permeability, and flammability. Additionally, the performance of the synthesized material, its surface functionalization, and its optical, magnetic, electrical, and dielectric properties are improved [9,10,11].

Despite having generally very poor mechanical properties, polymers are useful in applications where this property is necessary because of their flexibility. Under high strain, they typically deform when loaded. Using nanofillers with a very high aspect ratio and stiffness in a polymer matrix, it is possible to improve mechanical properties like tensile, strength, modulus, or stiffness [12]. Nano-composite polymers hold the potential for the development of a new class of lightweight hybrid materials with a wide range of uses in the automotive, general, and industrial sectors. Compared to conventional materials, it discusses the possibility of using them as radiation protection materials. To shield against different types of radiation, there is a demand for materials that are effective, lightweight, and sustainable.

Amana et al. [13] evaluated the radiation properties of the pure epoxy, Al2O3-epoxy and Fe2O3-epoxy exposed to various energies of gamma-rays (0.662, 1.173, and 1.333 MeV). The results explained an excellent agreement between the experimental and theoretical values. The proposed epoxy nano-composites with improved properties were affirmed to be potential for the γ-radiation shielding. Zhong et al. [14] fabricate a new material of ultrahigh molecular weight polyethylene (UMWPE) fiber-reinforced nano-epoxy composite. The results demonstrated that the insertion of graphitic nanofibers in the matrix had no effect on the excellent radiation shielding capability associated with UHMWPE. Also, there was an enhancement in the thermal and mechanical properties of the composite. Noor Azman et al. [15] investigate the effect of particle size of tungsten oxide–epoxy composites on the attenuation of the X-ray beam. They found that when compared to micro-sized WO3 with the same filler loading, nano-sized WO3 has a higher capacity to attenuate lower X-ray energy (22–35 keV). However, at higher X-ray energies, the effect of particle size on transmitted X-ray beam intensity was minimal (40–120 keV). Aldhuhaibat et al. [16] added gadolinium oxide to an epoxy matrix, which increases the mass attenuation coefficient of composites, and the improvement is stronger at low energy because of controlling photoelectric effect and K-edge of the element gadolinium. The effect of particle size is apparent obviously at the shielding ability, while nano-Gd2O3 composites have a better capacity to shield X- and γ-ray than micro-Gd2O3 composites, and an enhanced effect of ~ 28% is obtained with Gd2O3 content of around 5 wt.% at 59.5 keV.

In this study, we have manufactured discs using various thicknesses of micro- and nano-carbon/epoxy composites. Our objective is to investigate the composite's capability to shield gamma-rays. Furthermore, we have employed Scanning Electron Microscopy (SEM) and Transmission Electron Microscopy (TEM) assays to analyze the prepared samples.

2 Materials and method

2.1 Materials and sample preparation

The carbon powder is prepared from graphite rods, which are crushed and ground finely to a micro-size using a blender. Epoxy adhesive with 70% wt. of ratio 1:1 for resin and hardener, respectively, was mixed with 0, 10, and 30% wt. of carbon until it became a homogeneous mixture. The mixture was then poured into 3 cm diameter molds and allowed to dry at room temperature.

Nanocarbon powder was prepared using a ball mill machine (Photon company, Egypt), with a milling time of 35 h. The ratio of balls to powder is 10:1. Stainless steel balls of diameters 5, 10, and 20 mm are used as a milling medium. The milling speed was set at 600 rpm. Figure 1 shows the prepared samples with different weight percent of carbon.

Fig. 1
figure 1

a EPO 0%, 10%, and 30% wt. micro-carbon samples and b EPO 10% and 30% wt. nano-carbon samples

Full size image

2.1.1 Morphology

A) Scanning electron microscope (SEM).

For SEM analyses, a scanning electron microscope of JSM-5300, JEOL type was used. The SEM analysis was conducted at the Faculty of Science, Alexandria, Egypt. For scanning the samples were coated using an ion sputtering coating device then the samples were placed inside the electron microscope with operating voltage 20 keV and the magnification order was 150, 1000, and 20,000.

b) Transmission electron microscope (TEM).

TEM were performed for carbon NPs on JEOL JEM-2100 high resolution transmission electron microscope at an accelerating voltage of 200 kV. The TEM analysis was conducted at the Faculty of Science, Alexandria, Egypt.

2.1.1.1 Mechanical measurements

Mechanical measurements were executed for pure epoxy, epoxy/micro-carbon and epoxy/nano-carbon composites of area 100 mm2 using Devotrance Kalite kontrol ve test Cihazlari Ltd. equipment. Measurements occur at room temperature and the maximum load for all samples 50 KN of rate 1 mm/min. Table 1 shows loaded force for all samples.

Table 1 Loaded forces for all samples
Full size table

2.1.2 Attenuation parameters

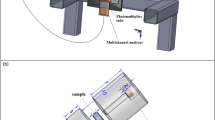
The shielding parameters were measured in an experiment which measured the intensity of the gamma-rays passed through the specimen. The detector that was used in this work was a NaI (Tl) scintillation detector. Figure 2 shows the schematic drawing of the narrow beam, where the source–detector distance was 300 mm and the detector–sample distance was 30 mm. A lead collimator with an outer diameter of 100 mm and an inner diameter of 8 mm was used as a house shield for the radioactive source. The five-point radioactive sources are used as follows; Am-241, Co-60, Ba-133, Cs-137, and Eu-152 emit a broad spectrum of energies from 0.06 to 1.408 MeV [17, 18]. The emitted photons interact with the detector crystal and transform into signals appearing in peaks in a spectrum using Genie 2000 software [19,20,21]. The acquisition time was extended to ensure a minimum of 20,000 counts were obtained under the full-energy peak, resulting in a statistical uncertainty of less than 1%. This deliberate approach ensured accurate measurements and reliable data analysis.

Fig. 2
figure 2

Sketching diagram of NaI(Tl) scintillation detector

Full size image

The area under each peak was calculated in the presence and absence of samples, which represent the transmitted (I) and initial (I0) intensities, respectively. Calculating the linear attenuation coefficient (LAC) is the first step to evaluating the material capability for shielding, using Beer–Lambert’s law [22]:

$$LAC=\frac{1}{t}\mathit{ln}\left(\frac{{I}_{0}}{I}\right),$$
(1)

where t is the thickness of the sample. The mass attenuation coefficient (MAC) was calculated by dividing the LAC for a given material by its density (ρ). The MAC of a composition can also be calculated using the following equation:

$${\text{MAC}}=(\mu /\rho )= {\sum }_{i}{w}_{i} {(\mu /\rho )}_{i},$$
(2)

where wi is the mass fraction of the ith constituent element in the sample. Using the XCOM program [24], the MAC was theoretically calculated and compared with the experimental values. Where ρ is the density of the material, wi and (μ/ρ)i are the weight fraction and mass attenuation coefficients of the ith constituent element, respectively. For chemical compounds, wi is given by:

$${{\text{w}}}_{{\text{i}}}=\frac{{{\text{A}}}_{{\text{i}}}{{\text{n}}}_{{\text{i}}}}{\sum_{{\text{i}}}{{\text{A}}}_{{\text{i}}}{{\text{n}}}_{{\text{i}}}} ,$$
(3)

where Ai is the atomic weight of the ith element and ni is the number of formula units. The theoretical MAC for the given samples was calculated by XCOM software code. The following equations present the relative deviations for the measured mass attenuation coefficient in relation to the XCOM result (Δ1) and the deviations between the micro- and nano-measured results (Δ2):

$${\Delta }_{1}\mathrm{\%}=\frac{{MAC}_{EXP} -{MAC}_{XCOM} }{{MAC}_{XCOM}}\mathrm{X }100,$$
(4)
$${\Delta }_{2} \%= \frac{{MAC}_{Nano}- {MAC}_{Micro}}{{MAC}_{Micro}} {\text{X}}100.$$
(5)

The half-value layer (HVL) is a very important parameter when making an appropriate radiation protecting substance. The parameter is the absorption thickness needed to decrease the incident radiation on the substance to 50% of its initial value and is calculated using the following equation:

$$HVL=\frac{\mathit{ln}2}{LAC}.$$
(6)

Also, the thickness at which the gamma-ray photons intensity entering the material decreases by a tenth is called the TVL and is given by:

$${\text{TVL}}=\frac{{\text{ln}}10}{{\text{LAC}}}.$$
(7)

The mean free path (MFP) which is defined as the distance between two successive interactions, is mathematically the inverse of the linear attenuation coefficient. The mean free path (MFP) was calculated for shielding material using the following equation:

$${\text{MFP}}=\frac{1}{{\text{LAC}}}.$$
(8)

The effect of the chemical composition of a photon shield is always elucidated using the effective atomic number, Zeff and its variation with energy may be used to investigate the relative changes in photon absorption processes with energy for diverse shields. Zeff was calculated from μ/ρ based on the following equation:

$${{\text{Z}}}_{{\text{eff}}}=\frac{{\sum }_{{\text{i}}}{{\text{w}}}_{{\text{i}}} {{\text{A}}}_{{\text{i}}} {\left(\frac{\upmu }{\uprho }\right)}_{{\text{i}}}}{{\sum }_{{\text{i}}}{{\text{w}}}_{{\text{i}}} \frac{{{\text{A}}}_{{\text{i}}}}{{{\text{z}}}_{{\text{i}}}} {\left(\frac{\upmu }{\uprho }\right)}_{{\text{i}}}}.$$
(9)

The effective electron density (Neff), measured in electrons/g, is defined as the number of electrons per unit mass of the material and is derived using the calculated Zeff according to the following equation:

$${{\text{N}}}_{{\text{eff}}}=\frac{{{\text{N}}}_{{\text{A}}}{{\text{Z}}}_{{\text{eff}}}}{<{\text{A}}>},$$
(10)

where \(<{\text{A}}>= \sum_{{\text{i}}}{{\text{f}}}_{{\text{i}}}{{\text{A}}}_{{\text{i}}}\) represents the mean atomic mass of the sample, and NA is Avogadro’s number.

When a gamma-ray beam is incident on a sample, the absorption and scattering interactions between the photon and the sample depend on the energy of the photon and the atomic number of the sample. These interactions give rise to secondary photons, which can potentially increase the photon flux. The buildup factor is a dimensionless quantity that is used to assess the impact of scattered radiation and the deposition of secondary photons in the process of protection. The buildup factors are separated into two types, the first type is the exposure buildup factor (EBF), which refers to the radiation exposure caused by the ionization of air due to photons. The second type is the energy absorption buildup factor (EABF), which refers to the amount of energy deposited in the attenuating medium. Buildup factors are obtained by computing them using the Geometrical Progression (GP) fitting method at energies ranging from 0.015 to 15 MeV, and these values are defined by Eqs. (13) and (14). First, it is very important to know about equivalent atomic number (Zeq) values, as this value must lie at a specific energy between (Z1 and Z2) atomic numbers (Z1 < Zeq < Z2), which is calculated by the following equation:

$${{\text{Z}}}_{{\text{eq}}}=\frac{{{\text{Z}}}_{1}\left({{\text{logR}}}_{2}-{\text{logR}}\right)+{{\text{Z}}}_{2}({\text{logR}}-{{\text{logR}}}_{1})}{{{\text{logR}}}_{2}-{{\text{logR}}}_{1}},$$
(11)

where Z1 and Z2 are atomic numbers of elements according to ratios R1 and R2, respectively. R is ratio MACCompton/MACTotal for the sample at same energy.

The computed Zeq values of the investigated materials were then used to interpolate the GP fitting EBF (b, c, a, XK, d) in the range of energy 0.015–15 MeV using the interpolation formula:

$${\text{C}}=\frac{{{\text{C}}}_{1}\left({{\text{logZ}}}_{2}-{{\text{logZ}}}_{{\text{eq}}}\right)+{{\text{C}}}_{2}({{\text{logZ}}}_{{\text{eq}}}-{{\text{logZ}}}_{1})}{{{\text{logZ}}}_{2}-{{\text{logZ}}}_{1}},$$
(12)

where C1 and C2 are GP fitting parameters, taken from the ANSI/ANS-6.4.3 standard database [22, 23] corresponding to Z1 and Z2 between which Zeq of the selected material lies.

Finally, the EBF for the selected samples were then estimated with the help of the obtained GP fitting parameters, using the following relations:

$${\text{B}}\left({\text{E}},{\text{x}}\right)=1+\left({\text{b}}-1\right)\frac{\left({{\text{K}}}^{{\text{x}}}-1\right)}{\left({\text{K}}-1\right)}\mathrm{ K}\ne 1,$$
(13)
$${\text{B}}\left({\text{E}},{\text{x}}\right)=1+\left({\text{b}}-1\right)\mathrm{x K}=1.$$
(14)

where

$${\text{K}}\left({\text{E}},{\text{x}}\right)={{\text{Cx}}}^{{\text{a}}}+{\text{d}}\frac{{\text{tanh}}\left(\frac{{\text{x}}}{{{\text{X}}}_{{\text{k}}}}-2\right)-{\text{tanh}}(-2)}{1-{\text{tanh}}(-2)}\mathrm{ x}\le 40\mathrm{ mfp},$$
(15)

where E is the incident energy at x mean free path, and \({\text{K}}\left({\text{E}},{\text{x}}\right)\) is the variation corresponding to the change in energy and spectrum shape.

3 Results and discussion

3.1 Microstructure analysis

The transmission image for nano-carbon material appears in Fig. 3. It showed that the average size of micro-carbon material was 0.3 ± 0.05 μm, while the average size of the nano-carbon was 20 ± 5 nm. Carbon nanoparticles have a random shape, but most of them are spherical.

Fig. 3
figure 3

Transmissions electron microscope of a micro-carbon material and b nano-carbon material

Full size image

The microstructures of the epoxy and epoxy filled with various contents of carbon black (10% carbon NPs, 10% carbon micro-size, 30% carbon NPs, and 30% micro-size) are displayed in Fig. 4. Figure 4a shows the fracture surface of the neat specimen is flat and smooth, which is characteristic of brittle fracture behavior and points to the low fracture toughness of the neat specimen. As Fig. 4b and c shows, when the carbon content is lower, the carbon black is separated within the epoxy matrix. As the carbon content increases, the carbon molecules more closely connect to each other, and a complete carbon array is gradually formed [18].

Fig. 4
figure 4

SEM of a EPO 0% C, b EPO 10% micro-C, c EPO 30% micro-C, d EPO 10% nano-C, and e EPO 30% nano-C

Full size image

Figure 4d and 4e demonstrates the presence of nano-carbon to the extent of 10% carbon and 30% carbon. Figure 4d shows that nano-carbon filled some portions of epoxy, therefore, when the amount of carbon increases, its distribution is better, as the nanocarbon particles fill and cover almost the entire epoxy matrix.

3.2 Mechanical measurements

According to Fig. 5a, the study sample's pure epoxy adhesive sample had the maximum applied force (P = 695 MPa). The epoxy adhesive's bearing strength will decrease when 10% micro-carbon is added because the applied load will drop to (P = 350 MPa). However, a sample containing 10% nano-carbon requires a greater applied force (P = 407 MPa) than a sample of micron size. In the same way, in Fig. 5b, it appears that the applied force of the 30% micro-carbon reduces to (P = 256 MPa) but increases again to (P = 366 MPa) by adding the 30% wt. nano-carbon. It suggests that adding carbon to epoxy adhesive makes it lose its adhesive qualities. The large size of the micro-particles may also agglomerate in one area, which would reduce the strength of the sample [22]. Nano size's impact on the samples was demonstrated by a comparison of micro- and nano-samples. The loaded force values increased for the 10% and 30% wt. samples, going from 350 to 407 and 256 to 366 MPa, respectively. Given that the distribution of nano-carbon within the epoxy particles is excellent and has very good uniformity, this demonstrates the extent to which the effect of nano-size on the mechanical properties of the examined samples. This was demonstrated by scanning electron microscope images of the samples. The mechanical qualities of the sample were destroyed when the percentage of powder in the sample increased, whether in the micro- or nano-size state, while these properties were noticeably improved when the percentage of nano increased [25].

Fig. 5
figure 5

Stress–strain values of a EPO 10% micro- and nano-C, b EPO 30% micro- and nano-C

Full size image

3.3 Attenuation calculation

To ensure the accuracy of the experimental findings, the experimental values of the mass attenuation coefficient (MAC) of the micro-composites and nano-composite were compared with the theoretical values using the XCOM program. The XCOM program utilizes the chemical composition of each sample to generate theoretical values. Table 2 presents the MAC values obtained from both the experimental and XCOM methods, along with the deviation between the two methods calculated using Eq. (4). Both methods are in perfect agreement with each other, with values ranging from 0.02% to 2%.

Table 2 Experimental and theoretical values of MAC at different photon energies and the measured densities for different composites
Full size table

Table 2 shows that as energy increases, the MAC values decrease. This trend refers to the various interaction possibilities of photons with materials, including the photoelectric effect, Compton scattering, and pair production. Also, with the increase in the percentage of micro-carbon, the value of the attenuation decreases, contrary to what is supposed, and this is due to epoxy carbon composites having a lower effective atomic number. Moreover, it is noted that the composite’s measured density increases with increasing the mass percentage of filler. This means that the combination of carbon and epoxy leads to an increase in its packing density. Furthermore, the findings revealed that the EPO /nano-C samples exhibited a higher absorption of photons compared to epoxy doped with micro-C particles. Additionally, epoxy/nano-sized C contained a greater number of C particles per gram in comparison to epoxy/micro-sized C. As a result, the distribution of nano-sized C within the epoxy is expected to differ from that of micro-sized C, leading to a more even dispersion in the epoxy. Consequently, the likelihood of photons interacting with and being absorbed by C particles is potentially greater in epoxy/nano-sized C than in epoxy/micro-sized C. This outcome aligns with the values of Δ2% in Table 2, where the MAC values of nano-composites surpass those observed in composites containing micro-carbon.

The relation of experimental and theoretical values of linear attenuation coefficient (LAC) with photon energy ranged from 0.059 MeV to 1.408 MeV for 0%, 10%, and 30% wt. of carbon plotted in Fig. 6 which shows the agreement of theoretical and experimental results.

Fig. 6
figure 6

Comparison between theoretical and experimental LAC for EPO 0%, 10%, and 30% micro-C

Full size image

The linear attenuation coefficient (LAC) is a density-dependent parameter that plays a crucial role in assessing the effectiveness of shielding materials in blocking gamma-rays. Figure 7 illustrates the pattern of the LAC for different samples as a function of photon energy. It shows that, as the carbon content of the composite rises, the LAC's value rises. Also, the measured LAC of epoxy/nano-C is higher compared to that of the micro-composite at the same weight percentage. All these observations relate to the increasing density. The LAC values in cm−1 for 10% C micro and nano, respectively, are as follows: 0.217 and 0.260 at 0.059 MeV, 0.093 and 0.106 at 0.662 MeV, and finally 0.065 and 0.071 at 1.408 MeV. While the LAC values in cm−1 for 30% C micro and nano, respectively, are as follows: 0.233 and 0.283 at 0.059 MeV, 0.104 and 0.121 at 0.662 MeV, and finally 0.0705 and 0.0783 at 1.408 MeV.

Fig. 7
figure 7

Relation of LAC with photon energy for different composites

Full size image

The atomic number of composite materials is not represented by an integer value as in the case of the elements but is a numerical quantity called the effective atomic number, which is calculated based on the percentage of the participation of each element in the composite material [26]. Figure 8a shows the relationship between effective atomic number and energy. As the energy increases, there is a corresponding decrease in Zeff. This can be attributed to the dependence on the mass attenuation coefficient (MAC). Additionally, when the carbon content increases, the values of Zeff also decrease. In the same way, the relation of the Neff values with the photon energy in the range of 0.059–1.4 MeV is presented in Fig. 8b, and one can notice that the behavior of Neff values is very similar to the trends identified for Zeff values. Neff values vary from 5.70 × 1025 to 7.04 × 1025 electrons/g at energy 0.059 MeV and from 5.22 × 1025 to 6.26 × 1025 electrons/g at energy 1.408 MeV for all prepared samples.

Fig. 8
figure 8

Variation of a Zeff and b Neff against photon energy for EPO 0%, 10% and 30% micro-C samples

Full size image

The MFP of epoxy with different amounts of micro- and nano-C as a function of photon energy is presented in Fig. 9. The MFP decreases as the amount of C increases. Furthermore, at a certain concentration, the MFP for epoxy with nano-C is lower than that for epoxy with micro-C. This finding implies that epoxy/ nano-C is more space-efficient than epoxy/ micro-C. Consequently, in our experiments, epoxy containing 30 wt. % nano-C is the best attenuator. However, at a specific concentration, we found that the MFP follows the trend: MFP0.059 MeV < MFP0.662 MeV < MFP1.4 MeV. The order mentioned in the MFP suggests that high-energy radiation can more easily penetrate through the epoxy containing micro- and nano-C. Therefore, it is preferable to use thicker epoxy to effectively block high-energy radiation.

Fig. 9
figure 9

The MFP of an epoxy and different weight fractions of micro- and nano-C at different energies

Full size image

The HVL results for the prepared carbon samples are plotted in Fig. 10. It is obvious that the HVL values increase with increasing energy. At energy 0.059 MeV, the HVL was for epoxy/0%, 10%, and 30% micro-carbon 3.33 cm, 3.18 cm, and 2.97 cm, as well as for epoxy/10% and 30% nano-carbon 2.66493 cm and 2.44324 cm, respectively, while at 0.662 MeV, it was 7.86 cm, 7.45 cm, and 6.67 cm for epoxy /0%, 10%, and 30% micro-carbon and 6.49 cm and 5.73 cm for epoxy /10% and 30% nano-carbon. Finally, at energy 1.408 MeV, the HVL for epoxy/ 0%, 10%, and 30% micro-carbon are 11.27 cm, 10.63 cm, and 9.83 cm, respectively, and for epoxy /10% and 30% nano-carbon, they are 9.66 cm and 8.85 cm, respectively. This phenomenon can be attributed to the increased density of nano-C samples in comparison to micro-C samples. As a result, the half-value layer (HVL) data can be summarized as follows: when working with limited space for the shield, employing epoxy with nano-C proves more advantageous. This is because a thinner specimen containing nano-C can effectively attenuate half of the incoming photons.

Fig. 10
figure 10

The HVL of an epoxy and different weight fractions of micro- and nano-C at different energies

Full size image

The TVL values of poxy/carbon samples are plotted in Fig. 11 to demonstrate the correlation between energy increase and TVL. Figure 11 reveals that TVL is influenced by photon energy, as higher incident photon energy leads to higher TVL values. Interestingly, at low-energy levels, the epoxy/30% nano-carbon sample exhibited the lowest TVL value, making it the most favorable sample. However, at medium- and high-energy levels, the epoxy/30% nano-carbon sample (ranging from 19.06 to 29.40 cm) performed the best. On the other hand, the epoxy sample without any carbon content (ranging from 26.13 to 37.44 cm) proved to be the least effective.

Fig. 11
figure 11

The TVL of an epoxy and different weight fractions of micro- and nano-C at different energies

Full size image

Depending on the incident energy, the equivalent atomic number parameter (Zeq) can change. It was used to identify a material's characteristics in terms of related constituents. The ratio of the Compton cross-section to the total cross-section (MACCompton/MACTotal) allows for the determination of the values of the materials' Zeq for a given energy [27, 28]. First, the (MACCompton/MACTotal) ratios for 23 distinct elements (atomic numbers 4–92) were determined for a range of energies from 0.015 to 15 MeV. These computations were done using the XCOM program. Equations can be used to do parabolic interpolation to determine the Zeq values [29]. Figure 12 illustrates the relation between photon energy and the Zeq values. It is clear that the Zeq reaches its maximum value for all samples at a gamma-ray energy of 1 MeV. However, the minimum value is achieved for the energy range E ≥ 2 MeV. The Zeq gradually increases with increasing energy in the range of 0.015 < E < 1 MeV, due to the Compton effect process. Then, it rapidly decreases with energy in the range E > 1 MeV, mainly due to the pair production effect.

Fig. 12
figure 12

Equivalent atomic number of the samples as a function of photon energy

Full size image

After that, interpolation can be used to get the GP fitting parameters, and the buildup factors are determined as the last step in the calculations. The energy absorption and exposure buildup factors (EABF and EBF) versus photon energy for penetration depths up to 40 mfp for different composites are shown in Figs. 13 and 14. Generally, the EABFs and EBFs have low values at low and high energies, while they reach the highest values at medium energies. These correlations can be explained through partial photon interactions in the examined energy region. For low-energy levels, since the photoelectric effect is the predominant process, the photons are mostly annihilated or lose their energy. For this reason, there is less photon buildup. The EABFs and EBFs of the samples then progressively rise. As the ratio of carbon in the content of epoxy increases, it is noted that the buildup factors reach a maximum at further energies. Compton scattering is a determinant at medium energies. Therefore, the generation of secondary photons is enhanced, resulting in larger EABF and EBF values. At high energies, similar to low energies, the photons disappear, or their energy is significantly reduced. Hence, EBF and EABF values display a downward trend after 1 MeV [29,30,31].

Fig. 13
figure 13

The variation of EABF with photon energy for different samples at 1, 15, 25, and 40 mfp

Full size image
Fig. 14
figure 14

The variation of EBF with photon energy for different samples at 1, 15, 25, and 40 mfp

Full size image

Also, Figs. 13 and 14 show that the lowest EABF and EBF values were seen at 1 mfp, while the highest values were seen at 40 mfp. According to the increasing penetration depth of the materials, this leads to an increase in the thickness of the interacting material, which in turn leads to an increase in the scattering events in the interacting medium, resulting in large EABF and EBF values [32, 33].

4 Conclusion

The present study utilized epoxy and carbon samples to fabricate radiation shields. When micro- and nano-carbon particles were introduced to epoxy, the composite became homogeneous as a result of the epoxy's ability to distribute the particles evenly. Furthermore, the contact between carbon and epoxy increases with an increase in carbon weight percentage. From mechanical data, we can conclude that by adding carbon powder to epoxy adhesive material, its strength will be decreased because the crosslinking between the epoxy matrix and the carbon powder will be weaker. It can be concluded that the decay in properties is mainly due to the clustering of particles due to an increasing level of reinforcement and porosity formation. But comparing the nano- and micro-carbon with the same wt.% we found enhancements in mechanical properties; however, increasing the weight of the powder still leads to weak bonding between the epoxy and the powder, even in the nano-composite’s samples.

The XCOM program was used to theoretically compare the mass attenuation coefficient between experimental and theoretical data, this comparison showed an extraordinary level of concordance. Also, the results show that the epoxy/0% carbon sample has the lower LAC value, while the epoxy/30% nano-carbon sample has the greater value. The epoxy/30% micro-carbon has a lower value than the epoxy/30% nano-carbon, as shown by TVL values, which follow the same pattern as HVL measurements in explaining the values of these two fractions. Moreover, the values of HVL and TVL rise in proportion to the weight percentage of carbon. Also, it was found that, for the samples under study, EBF values are at their highest in the region of intermediate energies, where Compton scattering is the predominant interaction. While EBF values are highest for epoxy alone (epoxy/0% carbon), Zeq values for the epoxy / 30% carbon sample are lowest, while EBF values are lowest for epoxy alone (epoxy/0% carbon). According to the findings, epoxy that has a high carbon content has good attenuation qualities.