Abstract
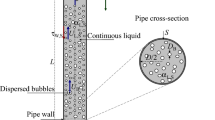
The drift-flux parameters such as distribution parameter and drift velocity are critical parameters in the one-dimensional two-fluid model used in nuclear thermal-hydraulic system analysis codes. These parameters affect the drag force acting on the gas phase. The accurate prediction of the drift-flux parameters is indispensable to the accurate prediction of the void fraction. Because of this, the current paper conducted a state-of-the-art review on one-dimensional drift-flux correlations for various flow channel geometries and flow orientations. The essential conclusions were: (1) a channel geometry affected the distribution parameter, (2) a boundary condition (adiabatic or diabatic) affected the distribution parameter in a bubbly flow, (3) the drift velocity for a horizontal channel could be approximated to be zero, and (4) the distribution parameter developed for a circular channel was not a good approximation to calculate the distribution parameter for a sub-channel of the rod bundle. In addition to the above, the review covered a newly proposed concept of the two-group drift-flux model to provide the constitutive equation to close the modified gas mixture momentum equation of the two-fluid model mathematically. The review was also extended to the existing drift-flux correlations applicable to a full range of void fraction (Chexel-Lellouche correlation and Bhagwat-Ghajar correlation).
Article PDF
Similar content being viewed by others
Change history
08 January 2021
An Erratum to this paper has been published: https://doi.org/10.1007/s42757-020-0094-y
13 October 2021
A Correction to this paper has been published: https://doi.org/10.1007/s42757-021-0126-2
08 January 2021
A Correction to this paper has been published: https://doi.org/10.1007/s42757-020-0094-y
05 February 2022
A Correction to this paper has been published: https://doi.org/10.1007/s42757-022-0132-z
References
Abbs, T., Hibiki, T. 2019. One-dimensional drift-flux correlation for vertical upward two-phase flow in a large size rectangular channel. Prog Nucl Energ, 110: 311–324.
Andersen, J. G. M., Chu, K. H. 1982. BWR refill-reflood program task 4.7: Constitutive correlations for shear and heat transfer for the BWR version of TRAC (No. NUREG/CR—2134). General Electric Co.
Bajorek, S. 2008. TRACE/V5.0 theory manual; field equations, solutions methods, and physical models. United States Nuclear Regulatory Commission.
Baotong, S., Rassame, S., Nilsuwankosit, S., Hibiki, T. 2019. Drift-flux correlation of oil-water flow in horizontal channels. J Fluid Eng, 141: 031301.
Barnea, D., Shoham, O., Taitel, Y., Dukler, A. E. 1980. Flow pattern transition for gas-liquid flow in horizontal and inclined pipes. Comparison of experimental data with theory. Int J Multiphase Flow, 6: 217–225.
Bhagwat, S. M., Ghajar, A. J. 2014. A flow pattern independent drift flux model based void fraction correlation for a wide range of gas-liquid two phase flow. Int J Multiphase Flow, 59: 186–205.
Borkowski, J. A., Wade, N. L., Rouhani, S. Z., Shumway, R. W., Weaver, W. L., Rettig, W. H., Kullberg, C. L. 1992. TRAC-BF1/MOD1 models and correlations (No. NUREG/CR—4391). Nuclear Regulatory Commission.
Brooks, C. S., Hibiki, T., Ishii, M. 2012a. Interfacial drag force in one-dimensional two-fluid model. Prog Nucl Energ, 61: 57–68.
Brooks, C. S., Ozar, B., Hibiki, T., Ishii, M. 2012b. Two-group drift-flux model in boiling flow. Int J Heat Mass Transfer, 55: 6121–6129.
Brooks, C. S., Paranjape, S. S., Ozar, B., Hibiki, T., Ishii, M. 2012c. Two-group drift-flux model for closure of the modified two-fluid model. Int J Heat Fluid Flow, 37: 196–208.
Chexal, B., Lellouche, G., Horowitz, J., Healzer, J., Oh, S. 1991. The Chexal-Lellouche void fraction correlation for generalized applications. Nuclear Safety Analysis Center of the Electric Power Research Institute, USA.
Chuang, T. J., Hibiki, T. 2015. Vertical upward two-phase flow CFD using interfacial area transport equation. Prog Nucl Energ, 85: 415–427.
Chuang, T. J., Hibiki, T. 2017. Interfacial forces used in two-phase flow numerical simulation. Int J Heat Mass Transfer, 113: 741–754.
Colebrook, C. F. 1939. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J Inst Civ Eng, 11: 133–156.
Goda, H., Hibiki, T., Kim, S., Ishii, M., Uhle, J. 2003. Drift-flux model for downward two-phase flow. Int J Heat Mass Transfer, 46: 4835–4844.
Grossetete, C. 1995. Fr Caractérisation expérimentale et simulations de l’évolution d’un écoulement diphasique à bulles ascendant dans une conduite vertical. Ph.D. Thesis. Châtenay-Malabry, Ecole centrale de Paris, France.
Hibiki, T., Ishii, M. 1999. Experimental study on interfacial area transport in bubbly two-phase flows. Int J Heat Mass Transfer, 42: 3019–3035.
Hibiki, T., Ishii, M. 2002a. Distribution parameter and drift velocity of drift-flux model in bubbly flow. Int J Heat Mass Transfer, 45: 707–721.
Hibiki, T., Ishii, M. 2002b. Interfacial area concentration of bubbly flow systems. Chem Eng Sci, 57: 3967–3977.
Hibiki, T., Ishii, M. 2003. One-dimensional drift-flux model for two-phase flow in a large diameter pipe. Int J Heat Mass Transfer, 46: 1773–1790.
Hibiki, T., Ishii, M. 2009. Interfacial area transport equations for gas-liquid flow. J Comput Multiphase Flows, 1: 1–22.
Hibiki, T., Ishii, M., Xiao, Z. 2001. Axial interfacial area transport of vertical bubbly flows. Int J Heat Mass Transfer, 44: 1869–1888.
Hibiki, T., Mishima, K. 2001. Flow regime transition criteria for upward two-phase flow in vertical narrow rectangular channels. Nucl Eng Des, 203: 117–131.
Hibiki, T., Ozaki, T. 2017. Modeling of void fraction covariance and relative velocity covariance for upward boiling flow in vertical pipe. Int J Heat Mass Transfer, 112: 620–629.
Hibiki, T., Rong, S. T., Ye, M., Ishii, M. 2003. Modeling of bubble-layer thickness for formulation of one-dimensional interfacial area transport equation in subcooled boiling two-phase flow. Int J Heat Mass Transfer, 46: 1409–1423.
Hibiki, T., Schlegel, J. P., Ozaki, T., Miwa, S., Rassame, S. 2018. Simplified two-group two-fluid model for three-dimensional two-phase flow computational fluid dynamics for vertical upward flow. Prog Nucl Energ, 108: 503–516.
Information System Laboratories. 2001. RELAP5/MOD3.3 code manual volume IV: Models and correlations. US NRC (NUREG/CR-5535/Rev 1-Vol.IV).
Ishii, M. 1977. One-dimensional drift-flux model and constitutive equations for relative motion between phases in various two-phase flow regimes. Report No. ANL-77-47. Argonne National Laboratory, USA
Ishii, M., Hibiki, T. 2010. Thermo-Fluid Dynamics of Two-Phase Flow, 2nd edn. Springer Science & Business Media.
Ishii, M., Mishima, K. 1984. Two-fluid model and hydrodynamic constitutive relations. Nucl Eng Des, 82: 107–126.
Julia, J. E., Hibiki, T. 2011. Flow regime transition criteria for two-phase flow in a vertical annulus. Int J Heat Fluid Flow, 32: 993–1004.
Julia, J. E., Hibiki, T., Ishii, M., Yun, B. J., Park, G. C. 2009. Drift-flux model in a sub-channel of rod bundle geometry. Int J Heat Mass Transfer, 52: 3032–3041.
Kalkach-Navarro, S. 1992. The mathematical modeling of flow regime transition in bubbly two-phase flow. Ph.D. Thesis. Rensselaer Polytechnic Institute, USA.
Kataoka, I., Ishii, M. 1987. Drift flux model for large diameter pipe and new correlation for pool void fraction. Int J Heat Mass Transfer, 30: 1927–1939.
Kondo, M., Kumamaru, H., Murata, H., Anoda, Y., Kukita, Y. 1993. Core void fraction distribution under high-temperature high-pressure boil-off conditions (No. JAERI-M-93-200). Japan Atomic Energy Research Institute.
Liu, H., Hibiki, T. 2017. Flow regime transition criteria for upward two-phase flow in vertical rod bundles. Int J Heat Mass Transfer, 108: 423–433.
Liu, H., Pan, L. M., Hibiki, T., Zhou, W. X., Ren, Q. Y., Li, S. S. 2018. One-dimensional interfacial area transport for bubbly two-phase flow in vertical 5×5 rod bundle. Int J Heat Fluid Flow, 72: 257–273.
Liu, T. T. 1989. Experimental investigation of turbulence structure in two-phase bubbly flow. Ph.D. Thesis. Northwestern University, USA.
Lokanathan, M., Hibiki, T. 2018. Flow regime transition criteria for co-current downward two-phase flow. Prog Nucl Energ, 103: 165–175.
Marchaterre, J. F. 1956. The effect of pressure on boiling density in multiple rectangular channels (Report No. ANL-5522). Argonne National Laboratory, USA.
Mishima, K., Ishii, M. 1984. Flow regime transition criteria for upward two-phase flow in vertical tubes. Int J Heat Mass Transfer, 27: 723–737.
Morooka, S. I., Yoshida, H., Inoue, A., Oishi, M., Aoki, T., Nagaoka, K. 1991. In-bundle void measurement of BWR fuel assembly by X-ray CT scanner. In: Proceedings of the 1st JSME/ASME Joint International Conference on Nuclear Engineering, Paper No. 38.
Ozaki, T., Hibiki, T. 2015. Drift-flux model for rod bundle geometry. Prog Nucl Energ, 83: 229–247.
Ozaki, T., Hibiki, T. 2018. Modeling of distribution parameter, void fraction covariance and relative velocity covariance for upward steam-water boiling flow in vertical rod bundle. J Nucl Sci Tech, 55: 386–399.
Ozaki, T., Suzuki, R., Mashiko, H., Hibiki, T. 2013. Development of drift-flux model based on 8×8 BWR rod bundle geometry experiments under prototypic temperature and pressure conditions. J Nucl Sci Tech, 50: 563–580.
Ozar, B., Dixit, A., Chen, S. W., Hibiki, T., Ishii, M. 2012. Interfacial area concentration in gas-liquid bubbly to churn-turbulent flow regime. Int J Heat Fluid Flow, 38: 168–179.
Ozar, B., Jeong, J. J., Dixit, A., Julia, J. E., Hibiki, T., Ishii, M. 2008. Flow structure of gas-liquid two-phase flow in an annulus. Chem Eng Sci, 63: 3998–4011.
Rassame, S., Hibiki, T. 2018. Drift-flux correlation for gas-liquid two-phase flow in a horizontal pipe. Int J Heat Fluid Flow, 69: 33–42.
Serizawa, A., Kataoka, I., Michiyoshi, I. 1991. Phase distribution in bubbly flow. In: Multiphase Science and Technology, Vol. 6. Hewitt, G. F., Delhaye, J. M., Zuber, N. Eds. Hemisphere, 257–301.
Taitel, Y., Bornea, D., Dukler, A. E. 1980. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J, 26: 345–354.
Vaidheeswaran, A., Hibiki, T. 2017. Bubble-induced turbulence modeling for vertical bubbly flows. Int J Heat Mass Transfer, 115: 741–752.
Yang, X., Schlegel, J. P., Liu, Y., Paranjape, S., Hibiki, T., Ishii, M. 2012. Measurement and modeling of two-phase flow parameters in scaled 8×8 BWR rod bundle. Int J Heat Fluid Flow, 34: 85–97.
Zuber, N., Findlay, J. A. 1965. Average volumetric concentration in two-phase flow systems. J Heat Transfer, 87: 453–468.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://doi.org/creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provided a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hibiki, T. One-dimensional drift-flux correlations for two-phase flow in medium-size channels. Exp. Comput. Multiph. Flow 1, 85–100 (2019). https://doi.org/10.1007/s42757-019-0009-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42757-019-0009-y