1 Introduction

As of April 2022 [1], more than 30.000 objects have been detected in geocentric orbit, with a steadily rising trend. The space traffic itself is also undergoing notable changes, particularly in Low Earth Orbits, fuelled by the miniaturisation of space systems and deployment of large constellations. Although less congested in terms of numbers, satellites in Geostationary Orbit (GEO) and services they provide us with (e.g., telecommunications, weather forecasting, television broadcasting) are also threatened by the problem of space debris, since the nearly absence of atmospheric drag makes impossible to rely on natural orbital decay of defunct objects.

Besides of debris mitigation guidelines, Active Debris Removal (ADR) and on-orbit servicing missions may represent a valid possibility in reducing orbital clutter. However, all these missions must counteract several technical challenges. Basically, a target with large angular momentum may lead to several problems, as an increase in the fuel necessary to circumavigate the object or in the danger of collision and further debris generation. Also, synchronizing with target’s motion, chasing a time-varying direction and docking are challenging mission phases, especially when dealing with uncooperative targets which may be “tumbling” (i.e., in a non-principal-axis spin state). These considerations underline that forecasting the target spin state that the spacecraft might encounter is crucial for success.

Nowadays, ground and space-based observations of space objects are used to investigate the spin state of a Resident Space Object (RSO). Light curves reconstructed by photometric data obtained by telescopes [2] can be combined with active techniques such as Satellite Laser Ranging (SLR) [3], Inverse Synthetic Aperture Radar (ISAR) images [4], or Doppler radar measurements [5] to acquire more information about the RSO spin rates and spin axis direction evolution in time.

In the past years, several studies have been dedicated to the analysis of rotational dynamics of space debris objects. ESA’s Environmental Satellite (Envisat) is probably one of the most studied in this sense, since it will likely be the target for an ADR mission in the next decades. In 2017, Lin et al. [6] found its spin axis to be stable in the orbital reference frame by optical observation data. Also, a secular increasing in the spin period was observed and justified by the combined effect of gravity-gradient and eddy current torques, dominant perturbations in lower orbits.

Decommissioned in 2006, TOPEX/Poseidon was observed by SLR in 2017 [7] and its inertial spin rate had increased from 0 to almost 6 rotations per minute over the period of 11 years. Among other perturbations, the Solar Radiation Pressure (SRP) is supposed to be the main factor responsible for this gain in rotational energy. When moving to GEO, SRP is often found to be the most significant external torque, especially in the case of objects equipped with wide solar panels. Earl et al. [8] provided a comparison among photometric observations of different box-wing satellites in GEO, namely Solidaridad 1, Telstar 401, EchoStar 2, and HGS-1. Although similar geometry and orbit, the RSOs were found to spin with unique spin periods with respect to one another. Secular spin period variations were found with different amplitude and timescale among the different satellites, sometimes in a quasi-cyclic trend. Such a strong variability suggested a large number of variables which may affect the rotational behavior of similar objects. In this sense, the family of retired Geostationary Operational Environmental Satellite (GOES) 8–12 represents an incredible case study. These five nearly identical defunct satellites mainly differ for the End-of-Life (EoL) configuration in terms of movable surfaces orientation. The objects show large diversity in spin state [9], with different spin periods and regimes, showing both principal-axis and tumbling spin states. This diversity was addressed to the large impact of movable surfaces orientation on the external torque generated by SRP and thermal re-emission, as modelled by the Yarkovsky–O’Keefe–Radzievskii–Paddack (YORP) effect [10].

In a more general approach, some solutions have been proposed to serve as simulators to analyze different RSOs. In 2015, The In-Orbit Tumbling Analysis tool (\(\iota\)OTA) [11] was proposed by Hyperschall Technologie Göttingen GmbH and Astronomical Institute of the University of Bern. More recently, an open-source coupled orbit-attitude propagation software, the Debris SPin/Orbit Simulation Environment (D-SPOSE), was presented by McGill University [12]. Both these tools are based on numerical integration of six-degrees-of-freedom coupled orbit and attitude motion of the object in Earth orbit. This approach is the most common but also the most expensive in terms of computational time and it may be not so accurate for long-term propagations because of accumulation of truncation errors over time. In this work, a different approach is presented, which relies on the tumbling-averaged model proposed in [13].

In Sect. 2, the theoretical framework is presented. Starting from the reference systems used in the work, the common Euler-based model and the above-mentioned averaged model are presented. In Sect. 3 the simulation set-up is described, with a presentation of geometries under analysis and estimates of their moments of inertia and Center of Mass location. In Sect. 4, results of long-term propagations on each of these objects are presented.

2 Theoretical Framework

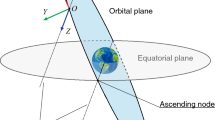
This study makes use of different reference frames, as represented in Fig. 1. First, the Heliocentric Coordinate System N: {\(\widehat{X_N}\),\(\widehat{Y_N}\),\(\widehat{Z_N}\) } is taken as inertial, with \(\widehat{X_N}\) pointing towards the intersection of ecliptic and equatorial planes, \(\widehat{Z_N}\) along the Earth’s orbital angular momentum vector and \(\widehat{Y_N}\) completes the right-handed system.

The rotating orbiting reference frame O: {\(\widehat{X_O}\),\(\widehat{Y_O}\),\(\widehat{Z_O}\) } is centered in the satellite with \(\widehat{X_O}\) parallel to the heliocentric orbit angular momentum vector, \(\widehat{Y_O}\) in the along-track direction and \(\widehat{Z_O}\) completes the right-handed system. In case of circular orbits, as it is in this work, \(\widehat{Z_O}\) is in the radial direction, pointing towards the Sun. The angular velocity of O with respect to N is \(\omega = n\widehat{X_O}\) where n is the heliocentric mean motion. Therefore, the rotation matrix can be expressed as \(\textit{ON} = R_2(-\pi /2)R_3(nt)\), denoting by \(R_i\) a rotation about the i-th axis and assuming \(t=0\) when the radial direction coincides with \({\widehat{X}}\).

The angular momentum reference frame H: {\(\widehat{X_H}\),\(\widehat{Y_H}\),\(\widehat{Z_H}\) } is centered in the satellite with \(\widehat{Z_H}\) along the satellite’s rotational angular momentum vector H. Being \(\alpha\) and \(\beta\), respectively, azimuth and elevation of \(\widehat{{\textbf {H}}}\) in the O frame, rotation from O to H can be expressed via the rotation matrix \(\textit{HO} = R_2(\beta )R_3(\alpha )\).

Finally, the satellite body reference frame B: {\(\widehat{X_B}\),\(\widehat{Y_B}\),\(\widehat{Z_B}\) } is centered in the satellite and fixed with it. Rotation from H to B is expressed by Euler angles in a \((3-1-3)\) rotation sequence, namely \(\textit{BH} = R_3(\phi )R_1(\theta )R_3(\psi )\), defining the precession \((\psi )\), nutation \((\theta )\) and rotation \((\phi )\) angles.

The same convention is applied for the principal axes reference frame P:{\(\widehat{X_P}\),\(\widehat{Y_P}\),\(\widehat{Z_P}\)} whose axes are aligned with the object’s principal axes of inertia (i.e., axes which make the inertia tensor diagonal).

Fig. 1
figure 1

Reference systems and rotations

Full size image

2.1 YORP Effect Model

The Yarkovsky–O’Keefe–Radzievskii–Paddack (YORP) effect [14] is one of the applications of the Yarkovsky effect [15]. It expresses the influence of thermal radiation force on asymmetric rotating bodies, provoking torques able to influence spin velocity and spin axis direction. Mainly analyzed for its capability of affecting spin period of small asteroids, its effect on defunct satellites in GEO has been investigated by Albuja et al. [16]. In this work, the YORP effect model derived in [17] is leveraged. It accounts for specular and Lambertian diffuse reflection, absorption, and instantaneous re-emission. The force acting on the ith facet of the satellite is expressed by

$$\begin{aligned} \pmb {f_i}&=-P_{SRP}\left\{ \left[ \rho _i s_i \left( 2\pmb {\hat{n_i}}\pmb {\hat{n_i}}^T - {\mathbb {I}}_{3x3} \right) \right. \right. \nonumber \\&\left. \left. \qquad +{\mathbb {I}}_{3x3} \right] \pmb {\hat{u}} + c_{d_i} \pmb {\hat{n_i}} \right\} A_i \text {max}\left( 0,\pmb {\hat{u}} \cdot \pmb {\hat{n_i}} \right) , \end{aligned}$$
(1)

where \(P_{SRP}\) is the Solar Radiation Pressure, \(\rho _i\) is the facet reflectivity, \(s_i\) is the fraction of reflectivity that is specular, \(\pmb {\hat{n_i}}\) is the unit vector normal to the facet and \(\pmb {\hat{n_i}}\pmb {\hat{n_i}}\) is a matrix outer product, \({\mathbb {I}}_{3x3}\) is the 3-by-3 identity matrix, \(\pmb {{\hat{u}}}\) is the satellite-Sun unit vector, \(A_i\) is the area of the ith facet, and \(c_{d_i}\) is defined as \(c_{d_i}=B(1-s_i)\rho _i + B(1-\rho _i)\) where B is the scattering coefficient (\(B=2/3\) for Lambertian reflection). The last portion of the expression, max(\(0,\pmb {{\hat{u}}} \cdot \pmb {\hat{n_i}}\)) is the illumination function, which ensures that only illuminated facets contribute to the total force.

Once the elementary forces have been estimated, the external torque due to YORP acting on the object is found by

$$\begin{aligned} {{\textbf {M}}} = \sum _{i=1}^{n_\mathrm{f}} \pmb {f_i} \times \pmb {r_i}, \end{aligned}$$
(2)

where \(n_\mathrm{f}\) is the number of facets used to discretize the object and \(\pmb {r_i}\) is the position vector from the facet centroid to the object center of mass.

2.2 Full Dynamics Model

The most common approach to propagate rotational dynamics of a rigid body relies on numerical integration of Euler’s equation coupled with the kinematic differential equation. In this work, numerical integration of Eqs. (3) and (4) will be referred to as propagation of “full dynamics”

$$\begin{aligned}{}[I]\pmb {{\dot{\omega }}} = -[\tilde{\omega }][I]\pmb {\omega } + {{\textbf {M}}} \end{aligned}$$
(3)
$$\begin{aligned} \begin{bmatrix} \dot{\beta _0}\\ \dot{\beta _x}\\ \dot{\beta _y}\\ \dot{\beta _z} \end{bmatrix} = \frac{1}{2} \begin{bmatrix} -\beta _x &{} -\beta _y &{} -\beta _z \\ \beta _0 &{} -\beta _z &{} \beta _y \\ \beta _z &{} \beta _0 &{} -\beta _x \\ -\beta _y &{} \beta _x &{} \beta _0 \end{bmatrix} \begin{bmatrix} \omega _1\\ \omega _2\\ \omega _3 \end{bmatrix}, \end{aligned}$$
(4)

where [I] is the body inertia matrix, \(\varvec{\omega }\) is the angular velocity of B with respect to N, M is the external torque found in Eq. (2), and \([\beta _0,\beta _x,\beta _y,\beta _z]\) is the quaternion expressing body’s inertial attitude (i.e., the relative attitude of B with respect to N).

Some disadvantages can be found in this formulation. First, it is computationally expensive, especially with large spin rates or if a stringent tolerance is required. Moreover, being \({\varvec{\omega }}\) and quaternion components relatively “fast” variables to be propagated, the truncation error may affect the reliability of the results for the long-term simulations which are presented in this work.

2.3 Tumbling-Averaged Model

In this work, the tumbling-averaged model which was derived by Benson et al. [13] is leveraged and is here summarized for clarity. It is based on description of rotational dynamics by means of four state variables.

First, the pole (i.e., rotational angular momentum) direction is identified by its spherical coordinates in the O frame, namely \(\alpha\) and \(\beta\), as shown in Fig. 1.

Another quantity of interest is the effective spin rate \(\omega _{\rm e}\) which scales linearly the components of \(\pmb {\omega }\) and is defined as

$$\begin{aligned} \omega _\mathrm{e} = \frac{2T}{H}, \end{aligned}$$
(5)

where T is the rotational kinetic energy \(T = \frac{1}{2}\pmb {\omega }\cdot [I]\cdot \pmb {\omega }\) and H is the rotational angular momentum vector \({{\textbf {H}}} = [I]\pmb {\omega }\).

The last state variable is the dynamic moment of inertia \(I_\mathrm{d}\), which is defined as

$$\begin{aligned} I_\mathrm{d} = \frac{H^2}{2T}, \end{aligned}$$
(6)

so that \(H=I_\mathrm{d}\omega _\mathrm{e}\) and \(T=\frac{1}{2}I_\mathrm{d}\omega _\mathrm{e}\).

The instantaneous value of \(I_\mathrm{d}\) with respect to the object principal moments of inertia defines its rotation regime among the different torque-free rotation modes as described in [18]. In this work, the long-axis convention is assumed, so \([I]=\text {diag}(I_\mathrm{i},I_\mathrm{s},I_\mathrm{l})\) with \(I_\mathrm{l}< I_\mathrm{i} < I_\mathrm{s}\). In the regimes of principal-axis rotation, the body is rotating about the maximum inertia axis for \(I_\mathrm{d}=I_\mathrm{s}\), about the intermediate one for \(I_\mathrm{d}=I_\mathrm{i}\) and about the minimum inertia axis for \(I_\mathrm{d}=I_\mathrm{l}\). Instead, the body is tumbling with \({\varvec{\omega }}\) precessing about the maximum inertia axis (i.e., short-axis mode or SAM) for \(I_\mathrm{i}<I_\mathrm{d}<I_\mathrm{s}\), while it is tumbling with \({\varvec{\omega }}\) precessing about the minimum inertia axis (i.e., long-axis mode or LAM) for \(I_\mathrm{l}<I_\mathrm{d}<I_\mathrm{i}\).

The equations of the model are derived starting from an application of the transport theorem to evaluate the derivative of H in the O frame

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \begin{bmatrix} H\cos \alpha \sin \beta \\ H\sin \alpha \sin \beta \\ H\cos \beta \end{bmatrix} =\left( \frac{\mathrm{d}{{\textbf {H}}}}{\mathrm{d}t}\right) _O = \left( \frac{\mathrm{d}{{\textbf {H}}}}{\mathrm{d}t}\right) _N - \pmb {\omega }_{\textit{O}/\textit{N}} \times {{\textbf {H}}}, \end{aligned}$$
(7)

where \(\left( \frac{\mathrm{d}{{\textbf {H}}}}{\mathrm{d}t}\right) _N={{\textbf {M}}}\) is the external torque and \(\pmb {\omega }_{\textit{O}/\textit{N}}=n\widehat{X_O}\) is the angular velocity of O with respect to N. Expressing all the quantities in the H frame and solving for \({\dot{\alpha }}\), \({\dot{\beta }}\), \({\dot{H}}\) leads to

$$\begin{aligned} {\dot{\alpha }}= & {} \frac{M_{Y_H} + Hn\cos \alpha \cos \beta }{H\sin \beta } \end{aligned}$$
(8)
$$\begin{aligned} {\dot{\beta }}= & {} \frac{M_{X_H} + Hn\sin \alpha }{H} \end{aligned}$$
(9)
$$\begin{aligned} {\dot{H}}= & {} M_{Z_H}. \end{aligned}$$
(10)

While the time derivative of \(I_\mathrm{d}\) can be expressed as

$$\begin{aligned} \dot{I_\mathrm{d}}=\frac{2I_\mathrm{d}}{H}{{\textbf {M}}} \cdot \left( {\mathbb {I}}_{3x3} - I_d[I]^{-1}\right) \hat{{{\textbf {H}}}}, \end{aligned}$$
(11)

where \({\mathbb {I}}_{3x3}\) is the 3-by-3 identity matrix, or equivalently

$$\begin{aligned} \dot{I_\mathrm{d}}=-\frac{2I_\mathrm{d}}{H}\left[ \frac{I_\mathrm{d}-I_\mathrm{i}}{I_\mathrm{i}}\alpha _{z1}M_1 + \frac{I_\mathrm{d}-I_\mathrm{s}}{I_\mathrm{s}}\alpha _{z2}M_2 +\frac{I_\mathrm{d}-I_\mathrm{l}}{I_\mathrm{l}}\alpha _{z3}M_3\right] , \end{aligned}$$
(12)

where \(M_1\), \(M_2\), and \(M_3\) are the external torque components in the P frame and [\(\alpha _{z1};\alpha _{z2};\alpha _{z3}\)] is the third column of the BH rotation matrix.

Assuming that \(\alpha\), \(\beta\), H, and \(I_\mathrm{d}\) evolve much slowly with respect to rotation of the object, Eqs. (8)–(12) are averaged over satellite’s tumbling motion assuming constant values for the averaged state variables \({\bar{\alpha }}\), \({\bar{\beta }}\), \({\bar{H}}\), \(\bar{I_\mathrm{d}}\). The tumbling-averaged equations of motion are so obtained

$$\begin{aligned}&\dot{{\bar{\alpha }}}=\frac{\overline{M_{Y_H}} + {\bar{H}}n\cos {\bar{\alpha }}\cos {\bar{\beta }}}{{\bar{H}}\sin {\bar{\beta }}} \end{aligned}$$
(13)
$$\begin{aligned}&\dot{{\bar{\beta }}}=\frac{\overline{M_{X_H}} + {\bar{H}}n\sin {\bar{\alpha }}}{{\bar{H}}} \end{aligned}$$
(14)
$$\begin{aligned}&\dot{{\bar{H}}}=\overline{M_{Z_H}} \end{aligned}$$
(15)
$$\begin{aligned}&\dot{\bar{I_d}}=-\frac{2\bar{I_d}}{{\bar{H}}}\left[ \frac{\bar{I_d}-I_i}{I_i}\overline{\alpha _{z1}M_1} + \frac{\bar{I_d}-I_s}{I_s}\overline{\alpha _{z2}M_2} +\frac{\bar{I_d}-I_l}{I_l}\overline{\alpha _{z3}M_3}\right] . \end{aligned}$$
(16)

The averaged torque components \(\overline{M_{X_H}},\overline{M_{Y_H}},\overline{M_{Z_H}},\overline{\alpha _{z1}M_1},\overline{\alpha _{z2}M_2},\overline{\alpha _{z3}M_3}\) have to be defined. Two methods are proposed to compute averaged torques, a numerical and a semi-analytical one. They both rely on the assumption that, being the external torque a small perturbation with respect to the satellite torque-free motion, average is computed over the torque-free motion (as expressed by the time evolution of the Euler’s angles \(\psi\), \(\theta\), \(\phi\)). Euler analytical solution for torque-free rotation of a rigid body [18] is leveraged in this work and is reported in Appendix 1. According to this solution, both nutation \(\theta\) and rotation \(\phi\) angles are driven by the scaled time parameter \(\tau\), while an independent formulation is required for the precession angle \(\psi\). Therefore, the average for a generic quantity F can be expressed as

$$\begin{aligned} \dot{{\overline{F}}} = \frac{1}{4K} \frac{1}{2\pi } \int _{0}^{4K} \int _{0}^{2\pi } {\dot{F}}\left( \psi ,\theta (\tau ),\phi (\tau )\right) \mathrm{d}\psi \mathrm{d}\tau \end{aligned}$$
(17)

being K the complete elliptic integral of the first kind [19] and 4K the period of the Jacobi elliptic functions \(\text {sn}\tau\) and \(\text {cn}\tau\) (see Appendix 1).

2.3.1 Numerical Tumbling-Averaged Model

In the numerical average approach, for each combination of the state variables \({\bar{\alpha }}\), \({\bar{\beta }}\), \({\bar{H}}\), \(\bar{I_\mathrm{d}}\), the external torque is averaged over a given number of body orientations obtained in a torque-free tumbling motion. It can be easily seen that \({\bar{\alpha }}\) and \({\bar{H}}\) do not impact the averaged torque, so the average is performed for \(\left( {\bar{\beta }}, \bar{I_\mathrm{d}}\right)\) combinations. In Fig. 2, a sequence of 10.000 attitudes is computed over 200 rotation periods in a possible LAM and reported both in \((\psi ,\theta ,\phi )\) and \((\tau ,\psi )\) phase spaces. As is evident, these orientations are more easily expressed as \((\tau ,\psi )\) combinations. Moreover, it seems that going further in time, the point will cover the whole \((\tau ,\psi )\) phase space (i.e., ergodicity); thus, averaging over the torque-free rotation is reduced to an area average over the \((\tau ,\psi )\) phase space.

Fig. 2
figure 2

10.000 torque-free orientations in a possible LAM state expressed in \((\psi ,\theta ,\phi )\) and \((\tau ,\psi )\) phase spaces

Full size image

In this work, average is computed over \(200 \times 200 (\tau ,\psi )\) orientations for each \(\left( {\bar{\beta }}, \bar{I_\mathrm{d}}\right)\) combination. Results are in the form of lookup tables \(\overline{M_*}=f({\bar{\beta }},\bar{I_\mathrm{d}})\), as it will be presented in Sect. 4.

2.3.2 Analytical Tumbling-Averaged Model

In the analytical average approach, a fully analytical expression is obtained starting from the YORP effect model of Eq. (1) by approximating the illumination function with its second-order Fourier transform, namely

$$\begin{aligned} \text {max}\left( 0,\pmb {{\hat{u}}} \cdot \pmb {\hat{n_i}} \right) \approx \frac{1}{3\pi } + \frac{1}{2} \left( \pmb {{\hat{u}}} \cdot \pmb {\hat{n_i}} \right) + \frac{4}{3\pi } \left( \pmb {{\hat{u}}} \cdot \pmb {\hat{n_i}} \right) ^2. \end{aligned}$$
(18)

Expanding Eq. (2) by substituting Eq. (18), including only nonzero terms, analytical expressions for the averaged torque components are finally obtained as expressed in Eq. (19). For the sake of brevity, in this work, only the expression of \(\overline{M_{X_H}}\) is reported

$$\begin{aligned} \begin{aligned} \overline{M_{X_H}}&=-P_\mathrm{SRP} \sum _{i=1}^{n_f} \left[ u_x\left( \frac{1}{2} c_{di} + \frac{1}{3\pi } c_{si} \right) \overline{d_xn_x}\right. \\&\left. + u_xu_z \left( c_{si} + \frac{8}{3\pi } c_{di} \right) \overline{d_xn_xn_z} + \right. \\&\left. \frac{4}{3\pi } c_{si} u_x^3 \overline{d_xn_x^3} + \frac{4}{\pi } c_{si}u_xu_z^2 \overline{d_xn_xn_z^2} + \frac{1}{2} c_{ai}u_xu_z\overline{r_yn_z}\right. \\&\left. + \frac{8}{3\pi } c_{ai}u_xu_z^2 \overline{r_yn_xn_z} \right] A_i, \end{aligned} \end{aligned}$$
(19)

where \(\pmb {d} = \pmb {r} \times \pmb {n}\), \(c_{si}=2\rho _is_i\), \(c_{ai}=1-\rho _is_i\) and all the averaged products can be expressed by elliptic function averages, which are well known in the literature [19]. A complete discussion can be found in [13].

3 Simulation Set-Up

This work deals with long-term YORP-driven rotational dynamics simulations of different Resident Space Objects (RSOs) in GEO. The objects are assumed to be placed in a circular heliocentric orbit at 1 AU, so \(P_\mathrm{SRP} = 4.56 \times 10^{-6} \mathrm{N}/\mathrm{m}^2\) in Eq. (1), while their geocentric orbit is neglected. Earth eclipses are also neglected, which is a reasonable assumption for satellites in GEO, since their maximum duration is estimated to be lower than 72 min per day.

For all the objects under analysis, a simplified 3D model of their external shape was reconstructed by an external software and imported in MATLAB in the form of .stl file. It allowed to work on a triangular facet model with precise orientation of facet unit normal vectors. The obtained faceted models are shown in Fig. 3.

Fig. 3
figure 3

Faceted models of objects under analysis. a GOES 8-12. b 3U CubeSat. c Rocket body. d Box-wing satellite

Full size image

In Fig. 3a, a faceted model of a GOES 8-12 satellite is shown. Accurate dimensions were found in the literature [20], as well as estimates of its principal moments of inertia and center of mass. It represents an interesting test case under YORP effect especially for its asymmetric shape, composed by the solar sail, the almost cubic bus and two movable surfaces, a wide solar panel and a small trim tab.

A 3U CubeSat with deployed solar panels is displayed in Fig. 3b. No specific object is taken as a reference, due to the variety of CubeSat configurations and to lack of notable examples of this kind of objects in GEO so far.

In Fig. 3c, the rocket body under analysis is shown. In this case, the Titan III-C Transtage served as a reference. Recently, the interest in this RSO has increased because of some documented fragmentation events [21]. Characteristic dimensions and masses were found in the literature or assumed by technical drawings [22], allowing for more accurate estimates of moments of inertia and center of mass. In particular, the actual cylindrical structure is simplified as an octagon to limit the number of facets, as well as the two engines outcoming from the structure. The other visible part is the extremity of the oxidizer tank, while the smaller fuel tank is stored inside and not visible.

The box-wing satellite model is displayed in Fig. 3d. Even though specific dimensions are taken from Optus B [23], results of this analysis can be likely applied to the wide variety of RSOs with this symmetric shape and a couple of wide solar panels.

As it is well known, parameters like inertia and center of mass location are fundamental when dealing with rotational dynamics. In this work, a large attention was addressed to their estimation. Only in the case of GOES, principal moments of inertia and center of mass location were found in the literature [13]. For the other objects, once mass and dimensions were assessed, a reasonable asymmetry in the bus due to internal equipment positioning was assumed, while other components were assumed to be perfectly symmetric. At this point, the center of mass was obtained as a weighted sum, while the inertia matrix was assessed by applications of the parallel axis theorem. Finally, principal inertias and corresponding axes were found by eigenvalues/eigenvectors analysis. Results are reported in Table 1.

Table 1 Mass parameters of objects under analysis
Full size table

According to Eq. (1) other fundamental input parameters to evaluate YORP effect are surface optical properties, namely the facet total reflectivity \(\rho\) and its specular fraction s. Reasonable values for these quantities for the different sections of the objects are taken from [9] and reported in Table 2.

Table 2 Surface optical properties
Full size table

4 Results

In this section, results of long-term propagations obtained by the model presented in Sect. 2.3 on geometries presented in Fig. 3 are reported.

4.1 GOES 8

In this work, simulations on GOES 8 have been performed to validate the correct implementation of the model.

Being extensively studied in [13], the GOES 8 satellite presents an EoL configuration with solar panel orientation \(\theta _\mathrm{sa}=17^{\circ }\) and trim tab orientation \(\theta _\mathrm{tt}=-60^{\circ }\), where \(\theta _\mathrm{sa}>0\) for rotations about \(-\widehat{Z_B}\) and \(\theta _\mathrm{tt}>0\) about \(\widehat{Y_B}\). The impact of movable surfaces orientation on the inertia matrix was properly considered, leading to \(I=\text {diag}[3432, 3570, 980] kg \cdot m^2\), which slightly differs from the one reported in Table 1.

In Fig. 4, the evolution of state variables for a 5-year propagation is shown. The assumed initial conditions are \(\omega _{e_0}=0.3 ^{\circ }/s\), \(I_\mathrm{d}=0.62I_\mathrm{s}\), \(\alpha _0=95^{\circ }\), \(\beta _0=50^{\circ }\). Results obtained with both the numerically averaged and the analytically averaged model are compared and they almost overlap: thus in the following figures, unless otherwise stated, results obtained by the analytical averaged model will be reported.

Fig. 4
figure 4

5-year propagation of GOES 8 by numerically (blue) and analytically (red) averaged models

Full size image

Results of this simulation are qualitatively similar to the ones obtained by Benson et al. [13]; thus, it is reasonable to assume that the models are correctly implemented. Particularly, this simulation shows a “tumbling cycle” performed by GOES 8. As the name suggests, this behavior is interesting for its unexpected periodicity. Starting from a tumbling condition, in the first 2 years, the satellite increases its angular velocity about the minimum inertia axis, so \(\omega _e\) increases, while \(I_d\) decreases. In the same period, the angular momentum direction is performing a relatively fast precession about the \(\widehat{Z_O}\) direction (i.e., the Sun direction) while increasing its elevation as visible from \({\dot{\alpha }}\) (preferred to \(\alpha\) for the seek of clarity) and \(\beta\) trend. As \(\beta\) becomes larger than \(90^\circ\), the overall trend changes and the object starts to slow down while moving to a uniform rotation condition (i.e., \(I_\mathrm{d}=1\)), which is reached in less than 4 years. At such a low spin rate, there is not enough pole stiffness, so YORP can drive the pole direction towards the Sun (i.e., \(\beta\) decreasing) in a relatively short amount of time, before a new tumbling cycle starts.

The temporal evolution of the angular momentum direction in both O and N reference frames is displayed in Fig. 5. It can be noticed that an apparently chaotic behavior in the inertial frame is instead a quite ordinate precession about the Sun direction in the Orbiting frame.

Fig. 5
figure 5

5-Year evolution of angular momentum direction from Fig. 4 in Orbiting (a) and Inertial (b) reference frames

Full size image

In Fig. 6, for a small part of the simulation shown in Fig. 4, the results of the averaged models were compared with the one obtained propagating the full dynamics as described in Sect. 2.2. It can be seen that the green curve shows qualitatively the same behavior, confirming the reliability of results obtained through the averaged models. Instead, a comparison among computational times underlines the large difference between the 75 min required to propagate the full dynamics for 6 months and the few seconds that are sufficient to propagate the averaged models.

Fig. 6
figure 6

Zoomed view of Fig. 4 and comparison with full dynamics results

Full size image

4.2 3U CubeSat

The CubeSat model under analysis is representative of a typical End-of-Life configuration with fully deployed solar panels. Even though, nowadays, there are few examples of such small objects in high orbits, the investigation was led to assess whether the combined effect of reduced exposed area and lower inertia led to a larger or lower impact of YORP on its long-term rotational dynamics.

A Monte Carlo analysis was performed to assess the probability of transition from uniform rotation about the maximum inertia axis to tumbling in less than 5 years. Transition to tumbling is supposed to be completed if the satellite goes below \(I_\mathrm{d}=I_\mathrm{i}\) (i.e., transition to SAM) at least once in the simulation. 100 random pole directions (i.e., \(\alpha _0\), \(\beta _0\)) were extracted for different Center of Mass locations and \(\omega _{e_0}\) and results are reported in Table 3.

Table 3 Monte Carlo results of CubeSat transition to tumbling within 5 years for different Center of Mass (row) and \(\omega _{{{e}_{0}}}\) (column)
Full size table

It can be seen a large impact of the initial spin rate in the first line, where this possibility of having a transition to tumbling in 5 years decreases from 89 to 10%, whereas it becomes negligible if the center of mass is too displaced from the symmetry axis as in the third line, where probability is above 87% even for a large initial angular velocity. Thus, to keep the object in a stable uniform rotation spin state, keeping the center of mass close to the symmetry axis was found to be more important than providing it with a large initial spin rate.

More in detail, for the specific case of \(\text {CoM} = \text {[3.66, 7.80, 46.6]} mm\), results of simulations for the only state variable of interest in this case, \(I_\mathrm{d}\), are shown in Fig. 7, where the dashed line is representative of \(I_\mathrm{d}=I_\mathrm{i}\).

Fig. 7
figure 7

CubeSat \(I_\mathrm{d}\) evolution for 100 randomly sampled pole directions with: a \(\omega _{{\rm e}_0}=6^{\circ }/\)s, b \(\omega _{{\rm e}_0}=8^{\circ }/\)s, and c \(\omega _{{\rm e}_0}=9^{\circ }/\)s

Full size image

A source of asymmetry can be introduced in the system by changing the optical properties of one of the bus facets, which was previously fixed to \(\rho =0.6\). This assumption seems reasonable, since one of these faces may be equipped with an antenna or a solar panel. In particular, the effect of a different reflectivity \(\rho\) has been assessed in Fig. 8 on a 20-year propagation with initial conditions \(\omega _{{\rm e}_0}=6^{\circ }/s\), \(I_{{\rm d}_0}=I_\mathrm{s}\), \(\alpha _0=250^{\circ }\), \(\beta _0=150^{\circ }\). Results show that such an asymmetry is likely to produce a faster and more chaotic behavior in the state variables. In particular, a possible tumbling-to-uniform rotation transition regime may start if a bus facet is provided with a low value of reflectivity such as \(\rho =0.27\).

Fig. 8
figure 8

Effect of \(+\widehat{Y_B}\) bus facet reflectivity on CubeSat 20-year propagation

Full size image

4.3 Box-Wing Satellite

The model for box-wing satellite is to be intended as representative of the large number of objects composed by an almost cubic bus and wide solar panels. As found in [9], orientation of these movable surfaces (\(\theta _{{\rm sp}_1},\theta _{{\rm sp}_2}\)) is supposed to have a large impact on long-term rotational dynamics. In this analysis, the satellite is assumed to be shut down with both solar panels pointing in the same direction (\(\theta _{{\rm sp}_1} = \theta _{{\rm sp}_2}\)) and the effect of \(\theta\) is investigated. The impact of solar panel orientation on the object inertia was properly taken into account, leading to a slightly different inertia matrix with respect to the one presented in Table 1.

In Fig. 9, a 20-year propagation with initial conditions \(\omega _{{\rm e}_0}=0.3^{\circ }/s\), \(I_{{\rm d}_0}=I_s\), \(\alpha _0=250^{\circ }\), \(\beta _0=160^{\circ }\) is displayed for \(\theta =40^{\circ }\), \(\theta =120^{\circ }\) and \(\theta =240^{\circ }\).

Fig. 9
figure 9

20-Year propagation of box-wing satellite dynamics for different solar panels orientation \(\theta\)

Full size image

Results show very different behaviors for different values of \(\theta\). The red line, representative of \(\theta =40^{\circ }\), shows the satellite needing about 10 years to transition from the initial uniform rotation to tumbling. Then, the object spins up about the long axis as shown since the very first years in the case of \(\theta =240^{\circ }\). Instead, for \(\theta =120^{\circ }\), a tumbling cycles-driven dynamics similar to the one described in [13] for GOES 8 is found. Here, the object comes back periodically to the starting uniform rotation conditions for a quite long period of time, which can be further investigated in future works.

A deeper analysis can be performed on the drivers of the averaged state variables evolution, which are the averaged torque components as shown by Eqs. (13)–(16). After numerical average operations, the averaged torque components are available in form of lookup tables \(\overline{M_*}=f({\bar{\beta }},\bar{I_\mathrm{d}})\) as it was described in Sect. 2.3.1. A larger dimensionality may be necessary to investigate the effect of another parameter, as it is \(\theta\) in this analysis. In Figs. 10 and 11, averaged torque components are displayed as functions of \({\bar{\beta }}\) and \(\theta\) for fixed values of \(\bar{I_\mathrm{d}}\). Solid black lines on the contours represent zero-value iso-level curves. Even if representing a section in the \(({\bar{\beta }},\bar{I_\mathrm{d}})\) plane, because of the low observed variability with \(\bar{I_\mathrm{d}}\), they can be intended as representative of all LAM and SAM configurations, respectively.

Fig. 10
figure 10

Averaged torque components for different \(\theta\) in LAM \((I_\mathrm{d}=5624 \mathrm{kg m}^2)\)

Full size image
Fig. 11
figure 11

Averaged torque components for different \(\theta\) in SAM \((I_\mathrm{d}=6572 \mathrm{kg m}^2)\)

Full size image

While the low variability of \(\overline{M_{Y_H}}\) with \(\theta\) in LAM will require a further investigation in future works, it can be noticed that torque approaches zero for unexpected symmetric configurations, such as \(\theta \approx \pm 40^{\circ }\) and \(\theta \approx 180^{\circ } \pm 40^{\circ }\). A similar result was found also in [13] with slightly different values. It confirms the idea that for objects of this kind, a preferable shut down epoch may be set to obtain a slower evolution in the post-disposal phase.

4.4 Rocket Body

Finally, the analysis on the rocket body model intended to explore the long-term behavior of such a large, quasi-oblate body. As for the CubeSat, the trade-off between area exposed to the Sun and inertia could lead to unexpected impact of YORP on this object. In Fig. 12, a possible 20-year evolution of this object is shown for initial conditions \(\omega _{{\rm e}_0}=0.15^{\circ }/s\), \(I_{{\rm d}_0}=0.8I_{\rm s}\), \(\alpha _0=254^{\circ }\), \(\beta _0=6^{\circ }\). A slow trend is observed, with \(\omega _{\rm e}\) steadily increasing, while \(I_{\rm d}\) and \(\beta\) seem to converge to a sort of equilibrium state.

Fig. 12
figure 12

20-Year propagation of rocket body dynamics

Full size image

To investigate this behavior, lookup tables of averaged parameters derivatives \(\dot{{\bar{\beta }}}\), \(\dot{{\bar{H}}}\), \(\dot{\bar{I_{\rm d}}}\) as function of \(\beta\) and \(I_{\rm d}\) were extracted and are reported in Fig. 13, where solid black lines represent zero-value iso-level curves. To remove dependency from \(\alpha\), \(\dot{{\bar{\beta }}}\) has been averaged over it. As it can be seen, the bottom-left corners of these contours show values close to 0, leading to the slow evolution which was observed in the simulation of Fig. 12. This underlines a possible low impact of YORP effect for this kind of objects, probably because of their intrinsic symmetry.

Fig. 13
figure 13

Averaged parameter derivatives as function of \(\beta\) and \(I_\mathrm{d}\)

Full size image

The evolution of angular momentum direction in the O frame is reported in Fig. 14, showing that pole evolution can be referred to a precession about a direction that is tilted with respect to the Sun direction (represented by the yellow dot) towards the out-of-plane direction. The green and the red dots are respectively the initial and final points of the evolution.

Fig. 14
figure 14

20-Year evolution of angular momentum direction from Fig. 12 in Orbiting reference frame

Full size image

5 Conclusions

In this work, a previously derived tumbling-averaged YORP rotational dynamics model has been applied to different geometries representative of Resident Space Objects in GEO. Leveraging an averaged model, long-term propagations up to 20 years could be performed in a computational time in the order of seconds, in a much faster approach with respect to numerical integration of full dynamics.

Analyses performed on GOES allowed us to confirm the compliance between the averaged approach and the propagation of full dynamics. The asymmetric shape of the satellite makes it an interesting target under YORP torque, since it exhibits tumbling cycles and a quite ordered evolution of pole direction in the Orbiting reference frame.

Studies on CubeSat quantified the impact of YORP according to Center of Mass location and initial spin rate. A Monte Carlo analysis showed that a high probability for this object to remain in uniform rotation in the first 5 years of the post-disposal phase can be reached only if the Center of Mass is kept close to the symmetry axis. Also, a possible impact of asymmetry in terms of reflective properties was explored.

The box-wing satellite model showed the large impact of End-of-Life solar array orientation on the long-term dynamics. The analysis confirmed the existence of symmetric solar panels orientations for which torque approaches zero, guaranteeing a slower evolution of the object in the post-disposal phase. Prediction of these favourable conditions can be of help in the definition of a preferable shut down epoch.

Finally, the large inertia and the intrinsic symmetry of the rocket body were found to prevent it from a fast rotational evolution. It suggested a low impact of YORP effect on the rotational dynamics of these objects.

In possible future applications, the model can be extended including other sources of external perturbation, such as internal energy dissipation due to flexible structures or fuel sloshing, while including also gravity gradient and magnetic torques can be useful to apply the model to RSOs in lower orbits. The accuracy in predicting long-term rotational behavior of debris objects other than GOES can be tested if accurate information about inertia and initial conditions are available.