1 Introduction

A spacecraft re-entering the atmosphere is exposed to extreme physical conditions. The severe heat loads acting on the surface material require the use of thermal protection systems (TPSs) allowing the flight vehicle to sustain itself in the environment for a given period of time [1]. TPSs are designed to give rise to physical-chemical phenomena capable of absorbing part of the heat. Ablative materials are largely used to this end because they are able to dissipate high heat fluxes by mass removal [2]. Ablation is mainly characterized by chemical reactions (oxidation, nitridation) and phase changes (melting, vaporization, sublimation), but the removal of solid mass may also be due to the thermomechanical erosion of the surface material (spallation).

Recently, strong mass efficiency requirements led to the development of a new class of low-density and porous TPMs, namely charring ablators [3], which also undergo pyrolysis, a thermo-chemical decomposition reaction which generates volatile compounds. As the virgin material reaches a high enough temperature (about 400 K), the resin begins to thermally decompose by means of endothermic reactions, leading to the production of pyrolysis gases. They percolate towards the boundary layer, such that a thermal barrier is generated in front of the heat shield due to the blowing effect. As the resin pyrolyses, it leaves a carbonaceous residue called char coating the carbon fibers. The char can be removed thermally (sublimation), mechanically (spallation) and, considering its high carbon content, it can undergo oxidation too [4]. Furthermore, while ablation of dense materials is usually described in terms of surface recession as the mass loss occurs superficially, in porous media, depending on physical conditions, ablation may be a volume phenomenon: oxidation, sublimation and spallation may occur inside the pores.

An example of porous charring TPM is the Phenolic Impregnated Carbon Ablator (PICA), used for the Stardust or Mars Science Laboratory missions and for the SpaceX Dragon capsule [5]. Another modern charring ablator is the Amorim’s cork-phenolic P50, successfully used for the Intermediate Experimental Vehicle (IXV) project and for the QubeSat for Aerothermodynamic Research and Measurements on AblatioN (qarman). The latter is an atmospheric entry demonstrator designed and manufactured for ESA by VKI to prove the potentiality of a CubeSat nanosatellite to test in flight environment the thermal protection capabilities of the new cork-based ablative TPMs. They can indeed count on the properties of cork, namely its elasticity, flexibility, compressibility, low density and low conductivity [6]. In particular, the cork P50 is an agglomerate of cork granules, bound together by a phenolic resin; the latter constitutes the filling matrix, while cork acts as a rigid precursor, as well as the carbon fibers in PICA. However, while in carbon-phenolic TPMs the resin is the only charring component, in cork-phenolic materials cork undergoes pyrolysis too. Moreover, cork is a swelling material: high temperatures let the cork achieve a proper viscoelastic state, so that it becomes sufficiently flexible to expand under the pressure of the pyrolysis gases trapped inside the pores [7]. This is an atypical behavior because most of the modern ablative TPMs, like PICA, do not exhibit the swelling phenomenon [8].

1.1 State of the Art

Considering the exceptionality of in-flight experiments and the complexity of reproducing in a ground facility the atmospheric re-entry conditions, numerical simulations represent an essential and powerful solution for investigating the behavior of TPMs. The first analyses and computational procedures for the simulation of charring ablative materials (CMA) were developed in the 1960s, through a series of NASA technical reports [9,10,11,12,13,14], providing solutions to couple the charring ablator response with a chemically reacting boundary layer. In the 1970s, these studies were continued with the contribution of Clark [15]. In the 1990s, the FIAT (Fully Implicit Ablation and Thermal-response) numerical tool was developed at NASA Ames Research Center [16], to perform one dimensional analysis of ablation and as sizing tool for TPMs. The capabilities of FIAT were also improved over the years [17,18,19]. In the 2000s, the TITAN (Two-dimensional Implicit Thermal-response and AblatioN) [20, 21] and the 3dFIAT codes [22, 23] were developed to extend the ablation simulations to two dimensions and three dimensions, respectively. However, even today most of the modern codes still dissociate the material response from the flow field and the interaction between these two environments is studied coupling two distinct solvers [24]. According to Turchi et al. [24] and Schrooyen [3], four numerical approaches can be identified: (1) material response solvers, (2) CFD codes solving only the flow field, (3) loosely coupled techniques to combine the first two methods and (4) fully coupled approaches, which represent the most appropriate solution for the simulation of highly porous TPMs, because they adopt a unified strategy to solve both the flow field and the material response within the same computational domain, allowing to treat ablation as a volume phenomenon. This is why Schrooyen [3] developed a continuum approach to treat the macroscopic flow through the porous medium. This unified approach was implemented within a multi-physics CFD code, argo, and a carbon preform material was thus simulated [25, 26]. Later, Coheur et al. [5] added a module for pyrolysis, to analyze a charring carbon-phenolic TPM and replicate the Theoretical Ablative Composite for Open Testing (TACOT) experiment [27,28,29].

This is the background in which the current work has to be set and the motivation behind it is to further enhance the capabilities of argo. A new method of computing the pyrolysis gas should be developed, since its chemical composition has been treated as known and constant so far. A further goal is to make argo capable of treating cork-phenolic TPMs, which are noted to swell. Martinez [30] conducted a literature review of swelling for porous materials and performed some numerical tests in matlab, showing the necessity to develop a physical model ensuring the solid mass conservation. Hence, two main objectives will be pursued in this work, according to the two physical phenomena to be studied: pyrolysis and swelling. In Sect. 2.3, a method to compute the chemical composition of pyrolysis gases will be proposed, rather than fixing it for the whole simulation. Specifically, a function calling the VKI library mutation++ was implemented within argo, to compute the species mass fractions of pyrolysis gases at equilibrium. It should be noted that this accurate approach is not necessarily applicable only to cork-phenolic TPMs, but to carbon-phenolic ones too. Section 2.4 concerns the development of a physical model accounting for swelling of porous cork-based TPMs. Such a model was implemented in a matlab code to be numerically tested.

2 Physical Modeling

In this work, the interaction between a high-enthalpy flow and a reactive porous medium was studied through a strong coupling strategy, to gradually progress from the pure fluid region to the solid porous one. The governing equations of fluid dynamics specialized for aero-thermal flows will be first presented. After the flow modeling part, the discussion will deal with the reactive porous material, followed by an extension to cork-phenolic specific phenomena. In particular, the development of a new feature to compute the pyrolysis gas in argo is treated and, finally, an original but preliminary idea to model the swelling behavior is described.

2.1 Navier–Stokes Equations for Chemical Non-equilibrium Flow

Atmospheric entry involves high-temperature and high-speed flows. Ablation typically takes place at low altitudes along the re-entry trajectory, below 60 km [3], where the continuum hypothesis is still valid. Such a flow is described by the Navier–Stokes equations for a viscous, high-temperature, chemically reacting and nonequilibrium flow. In argo, only chemical nonequilibrium is considered, whilst thermal nonequilibrium has not been included yet. A compact form for the system of governing equations can be adopted [3]:

$$\begin{aligned} \frac{\partial \varvec{{U}}}{\partial t}+\nabla \cdot \varvec{{F}}^c=\nabla \cdot \varvec{{F}}^d +\varvec{{S}}, \end{aligned}$$
(1)

where

$$\begin{aligned} \begin{aligned}&\varvec{{U}}= \begin{pmatrix} \rho _i \\ \rho \varvec{{u}} \\ \rho E \end{pmatrix} , \quad \varvec{{F}}^c= \begin{pmatrix} \rho _i \varvec{{u}} \\ \rho \varvec{\mathrm {uu}}+P\varvec{\mathrm {I}} \\ \rho \varvec{{u}}H \end{pmatrix} , \\&\varvec{{F}}^d= \begin{pmatrix} - \varvec{\mathrm {J}}_i \\ \varvec{{\tau }} \\ \varvec{{\tau }}\cdot \varvec{{u}}-\varvec{\mathrm {q}} \end{pmatrix} , \quad \varvec{{S}}= \begin{pmatrix} \dot{\omega }_i \\ 0 \\ \dot{\omega }_T \end{pmatrix}. \end{aligned} \end{aligned}$$
(2)

They are the vectors of conservative variables, convective fluxes, diffusive fluxes and source terms, respectively. Given the multispecies nature of a chemical non-equilibrium flow, a mass conservation equation has to be solved for each chemical species. Hence, considering \(N_s\) species, \(\rho _i\) is the density of each gaseous species, \(\varvec{{u}}\) is the velocity vector, \(\varvec{\mathrm {J}}_i\) is the species diffusion flux vector, \(\dot{\omega }_i\) is the chemical source term, P is the thermodynamic pressure, \(\varvec{{\tau }}\) is the viscous stress tensor, \(E=e+\varvec{u}^2/2\) is the total (non-chemical) energy per unit mass, H is the total (non-chemical) enthalpy per unit mass, \(\varvec{\mathrm {q}}\) is the heat flux vector and \(\dot{\omega }_T\) is the energy contribution related to the chemical production term [3, 25].

The system (1) also requires knowledge of thermodynamic and transport properties, as well as chemical kinetics. Within argo, the evaluation of physico-chemical properties can be realized through a coupling with the VKI external library mutation++ (MUlticomponent Thermodynamic And Transport properties for IONized plasmas in C++) [31]. When it is used as a routine within a CFD code like argo, an additional system of differential equations is solved, after reading the reaction mechanisms. The thermodynamic data of chemical species are computed by mutation++ through the NASA polynomial database, which provides a fitting of the thermodynamic properties of each species as a function of temperature. This allows to define the energy contribution related to the chemical source term [3, 25]:

$$\begin{aligned} \dot{\omega }_T=-\sum _{i=1}^{N_s} \dot{\omega }_ih_{f,i}^0, \end{aligned}$$
(3)

where \(h_{f,i}^0\) is the formation enthalpy of each species at a reference temperature \(T_0\). mutation++ is also able to accurately compute transport properties and coefficients by means of kinetic theory and, specifically, solving collision integrals derived from the Chapman–Enskog solution of the Boltzmann equation [3, 31]. Finally, a chemical kinetic model is required for the computation of the chemical reaction rates, to evaluate the production terms due to homogeneous reactions. For air, temperatures above 2000 K can indeed cause dissociation and exchange reactions. Considering \(N_r\) reactions, the production rate related to each species can be written as [3, 26]

$$\begin{aligned} \dot{\omega }_i^{\text {hom}} = W_i \sum _{k=1}^{N_r}(\nu ''_{i,k}-\nu '_{i,k})\Bigg (k_{f,k}\prod _{j=1}^{N_s}\tilde{\rho }_j^{\nu '_{j,k}} - k_{b,k}\prod _{j=1}^{N_s}\tilde{\rho }_j^{\nu ''_{j,k}} \Bigg ), \end{aligned}$$
(4)

where \(W_i\) is the molecular weight of each species, \(\nu _i\) is the stoichiometric mole number associated with the ith species, the superscripts \('\) and \(''\) indicate reactants and products respectively, while \(\tilde{\rho }\) is the molar density. Finally, \(k_{f,k}\) and \(k_{b,k}\) are respectively the forward and backward (or reverse) reaction rates, which can be measured experimentally and expressed by means of an Arrhenius law [3, 25, 26].

2.2 Reactive Porous Media: The Volume Averaging Theory

Within argo platform, the method of volume averaging is applied to derive continuum Navier–Stokes equations for multiphase systems, such that equations are locally averaged in volume or, in other terms, they are spatially smoothed to be valid everywhere [32]. A two-phase system is considered (Fig. 1): a gaseous phase (denoted with subscript g) and a solid one (denoted with s). The equations describing each phase are averaged over a Representative Elementary Volume (REV), assumed to be much larger than the characteristic size of the pores but much smaller than the domain [33]. The result is that the volume averaged quantities are continuous in space and the macroscopic behavior is modeled [3, 33]. An averaging volume \(\mathrm {d}V\) can be defined considering the presence of the two different phases [3]:

$$\begin{aligned} \mathrm {d}V=\mathrm {d}V_g+\mathrm {d}V_s. \end{aligned}$$
(5)

The volume fractions are defined as follows [3]:

$$\begin{aligned} \epsilon _g=\frac{\mathrm {d}V_g}{\mathrm {d}V}, \quad \quad \epsilon _s=1-\epsilon _g=\frac{\mathrm {d}V_s}{\mathrm {d}V}, \end{aligned}$$
(6)

where \(\epsilon _g\) is known as porosity and describes the void fraction, while \(\epsilon _s\) is the solid volume fraction. The superficial average of a quantity \(\alpha\) on a generic phase \(\gamma\) is defined as [3]

$$\begin{aligned} {\langle \alpha \rangle } = \frac{1}{\mathrm {d}V}\int _{\mathrm {d}V_\gamma }{\alpha \ \mathrm {d}V}, \end{aligned}$$
(7)

while the intrinsic average is

$$\begin{aligned} {\langle \alpha \rangle }_\gamma = \frac{1}{\mathrm {d}V_\gamma }\int _{\mathrm {d}V_\gamma }{\alpha \mathrm {d}V}. \end{aligned}$$
(8)

A relation between the two averages exists:

$$\begin{aligned} {\langle \alpha \rangle } = \epsilon _\gamma {\langle \alpha \rangle }_\gamma . \end{aligned}$$
(9)
Fig. 1
figure 1

The physical problem is modeled as a two-phase system. Image from [3]

Full size image

The volume averaging theory can be applied to the system of Eq. (1), to obtain the Volume Averaged Navier–Stokes equations (VANS), written in terms of volume fractions. The full derivation of VANS for a non-charring material can be found in the work of Schrooyen [3], who modeled ablation of a carbon preform using a cylindrical model for the carbon fibers and assuming recession to be uniform and radial, as sketched in Fig. 2.

Fig. 2
figure 2

Recession model implemented within argo. Carbon fibers are considered as cylindrical and the recession (due to oxidation reactions) is assumed to be uniform and radial. Credits: [3]

Full size image

The production rate due to heterogeneous reactions, namely oxidation, is modeled assuming an irreversible first-order reaction and it is given by Schrooyen [3]:

$$\begin{aligned} \langle \dot{\omega }^{\text {het}}\rangle = \sum _{i=1}^{N_s} \langle \dot{\omega }_i^{\text {het}} \rangle =-S_fk_f {\langle \rho _A \rangle }_g, \end{aligned}$$
(10)

where \(k_f\) is the forward reaction rate, \({\langle \rho _A \rangle }_{gs}\) is the area averaged density on the surface of the solid phase and \(S_f=2\sqrt{\epsilon _{s,0} \epsilon _s}/r_0\) is the specific (volumetric) surface of the carbon fibers [3]. Therefore, if \(r_0\) and \(\epsilon _{s,0}\) are the initial radius and the initial solid volume fraction, tracking the change in \(\epsilon _s\) the recession of the fibers due to oxidation can be directly computed through a geometrical procedure.

An extension to charring ablators was later added to model pyrolysis and it is briefly described in the following.

2.3 Model for Pyrolysis

The thermal decomposition of charring ablators was modeled and implemented within argo by Coheur et al. [5]. A scheme of the model is shown in Fig. 3. The virgin material, a carbon-phenolic TPM, is characterized by a structure of cylindrical carbon fibers filled with a phenolic resin. Given the presence of two solid components, the average solid density was re-defined as follows [5]:

$$\begin{aligned} \langle \rho _s \rangle = \langle \rho _f \rangle + \langle \rho _m \rangle , \end{aligned}$$
(11)

where \(\langle \rho _f \rangle\) is the average solid density of the fibers, while \(\langle \rho _m \rangle\) is the one of the resin matrix. In terms of solid volume fractions [5]:

$$\begin{aligned} \epsilon _s {\langle \rho _s \rangle }_s = \epsilon _f {\langle \rho _f \rangle }_f + \epsilon _m {\langle \rho _m \rangle }_m, \end{aligned}$$
(12)

where \(\epsilon _f\) and \(\epsilon _m\) are, respectively, the volume fractions of the fibers and the resin.

Fig. 3
figure 3

Model for pyrolysis implemented within argo, to treat carbon-phenolic ablators. Figure taken from [5]

Full size image

The production rate of pyrolysis is expressed through a number \(N_p\) of pyrolysis reactions of the resin matrix [5, 34]:

$$\begin{aligned} \langle \rho _m \rangle = \sum _{I=A}^{N_p}\langle \rho _I \rangle , \end{aligned}$$
(13)

where \(\langle \rho _I \rangle\) is the average solid density of the resin compound I. The decomposition rate of the compound I can thus be described by an Arrhenius law [5]:

$$\begin{aligned} \frac{\partial }{\partial t}\langle \rho _I \rangle = -A_{0,I}\langle \rho _I^v \rangle \exp {\Big (\frac{-E_{a,I}}{\mathcal {R}T}\Big )} {\Big ( \frac{\langle \rho _I \rangle -\langle \rho _I^c \rangle }{\langle \rho _I^v \rangle }\Big )}^{n_I}. \end{aligned}$$
(14)

Furthermore, a progress variable \(\xi _I\) is defined to describe each pyrolysis reaction, i.e. the local decomposition state of the material:

$$\begin{aligned} \xi _I=\frac{\langle \rho _I^v \rangle -\langle \rho _I \rangle }{\langle \rho _I^v \rangle -\langle \rho _I^c \rangle }, \quad \quad \xi =\sum _IF_I^v\xi _I . \end{aligned}$$
(15)

The source term due to pyrolysis \(\langle \dot{\omega }^{\text {pyro}}\rangle\) is thus computed by considering all the pyrolysis reactions of each resin compound [5]:

$$\begin{aligned} \langle \dot{\omega }^{\text {pyro}}\rangle = \sum _{I}^{N_p} \langle \dot{\omega }^{\text {pyro}}_I\rangle = \sum _{I}^{N_p}\frac{\partial }{\partial t}\langle \rho _I \rangle . \end{aligned}$$
(16)

When pyrolysis occurs, a carbonaceous residue is left, so a model of char surrounding the cylindrical carbon fibers was implemented [5], as shown in Fig. 3. Hence, the oxidation of carbon fibers takes place only once the char has been totally removed. An equivalent radius \(r_e\) is defined [5]:

$$\begin{aligned} r_e=r_{f,0}+e_c = r_{f,0} \sqrt{\frac{\epsilon _s}{\epsilon _{f,0}}}, \end{aligned}$$
(17)

where \(r_{f,0}\) is the initial radius of the fibers, while \(e_c\) is the additional thickness due to the formation of char, which simply depends on the amount of carbonaceous residue that one decides to leave after pyrolysis.

The system of VANS equations is thus obtained by specifying the vectors of Eq. (1) as follows [5]:

$$\begin{aligned} \varvec{{U}}=&\begin{pmatrix} \epsilon _g {\langle \rho _i \rangle }_g \\ {\langle \rho \varvec{{u}}\rangle }_g \\ \langle \rho E_{\text {tot}} \rangle \\ \langle \rho _f \rangle + \sum _{I=1}^{N_p}\langle \rho _I \rangle \end{pmatrix}\\ \varvec{{F}}^c=&\begin{pmatrix} \epsilon _g {\langle \rho _i \rangle }_g {\langle \varvec{{u}}\rangle }_g \\ {\langle \rho \rangle }_g {\langle \varvec{{u}}\rangle }_g {\langle \varvec{{u}}\rangle }_g + P \\ \epsilon _g{\langle \rho \rangle }_g {\langle H \rangle }_g {\langle \varvec{{u}}\rangle }_g \\ 0 \end{pmatrix} \\ \varvec{{F}}^d=&\begin{pmatrix} -{\langle \varvec{{J}}\rangle }_i \\ {\langle \varvec{{\tau }}\rangle }_g \\ \langle \varvec{{\tau }} \cdot \varvec{{u}}\rangle +\lambda _{\text{eff}}\nabla \langle T \rangle -\sum _{i=1}^{N_s}h_i{\langle \varvec{{J}}\rangle }_i\\ 0 \end{pmatrix} \\ \varvec{{S}}=&\begin{pmatrix} \epsilon _g {\langle \dot{\omega }_i^{\text{hom}}\rangle }_g + \langle \dot{\omega }_i^{\text {het}} \rangle + \sum _{I=1}^{N_p} m_{i,I} \langle \dot{\omega }^{\text {pyro}}_I\rangle \\ {{\varvec{F}_{\varvec{gs}}}} \\ -\sum _{i=1}^{N_s}\Big (\epsilon _g {\langle \dot{\omega }_i^{\text {hom}}\rangle }_g + \langle \dot{\omega }_i^{\text {het}} \rangle + \sum _{I=1}^{N_p} m_{i,I} \langle \dot{\omega }^{\text {pyro}}_I\rangle \Big )h_{f,i}^0 \\ -\sum _{i=1}^{N_s} \langle \dot{\omega }_i^{\text {het}} \rangle - \sum _{I=1}^{N_p} m_{i,I} \langle \dot{\omega }^{\text {pyro}}_I\rangle . \end{pmatrix} \end{aligned}$$
(18)

They are numerically solved by means of a Discontinuous Galerkin Method (DGM), a numerical technique combining the Finite Volume (FVM) and the Finite Element (FEM) methods. The advantages of both of these approaches are merged together, to offer a modern numerical method characterized by high order of accuracy on unstructured grids, computational efficiency, robustness, compactness and scalability [3, 35].

The implementation of these equations made argo capable of treating charring carbon-phenolic TPMs, like PICA. Concerning cork-phenolic ablators such as the cork P50, a further development is required because the P50 undergoes thermal degradation of both cork and phenolic resin. This process leads to the formation of carbon fibers (not present in the virgin material) and the carbonaceous residue. The implementation of a new model requires a considerable effort and it is beyond the scope of this work. For this reason, the main contribution to pyrolysis modeling of this work consists in the definition of an accurate method to compute the pyrolysis production rate \(\pi _i\) for each chemical species [5]:

$$\begin{aligned} \pi _i = m_{i,I} \ \langle \dot{\omega }^{\text {pyro}}_I\rangle . \end{aligned}$$
(19)

The species mass fractions \(m_{i,I}\) are unknown and they should be determined from experimental data, since they are not available in literature [5]. To date, the species mass fractions \(m_{i,I}\) were pre-fixed and hard-coded, such that the chemical composition of pyrolysis gas has been treated as known and constant so far. This is a strong assumption, as the composition of pyrolysis gases actually is a function of the local thermodynamic conditions and elemental composition. Considering that pyrolysis gases flow at relatively low speeds inside the porous medium [36], a very common assumption in the literature is to impose the production of volatile compounds of pyrolysis at thermochemical equilibrium. Therefore, a new routine was implemented within argo, to provide mutation++ the local temperature and pressure so that, starting from the elemental composition of pyrolysis gases, mutation++ is able to compute \(m_{i,I}\) at the local thermochemical equilibrium (Fig. 4). The elemental mass conservation is applied to compute the composition of the mixture depending on temperature, pressure and elemental composition [3]:

$$\begin{aligned} Y_i=Y_i(P,T,\upchi _j), \end{aligned}$$
(20)

where \(\upchi _j\) is the elemental mass fraction, \(j=1,... , N_e\) and \(N_e\) is the number of chemical elements.

Fig. 4
figure 4

Scheme of the new routine for the computation of pyrolysis production rate

Full size image

This procedure shifts the problem towards the evaluation of the elemental composition \(\upchi _j\) of pyrolysis gases, which should be determined experimentally.

2.4 Model for Swelling

The research of a physical model capable of predicting the swelling behavior of cork-phenolic TPMs drives this part of the work. The method investigated here should have certain features which make it suitable for the implementation in argo, as a future task. In particular, it should be based on a continuum approach, to be representable through equations valid over the whole domain of computation. A simplified strategy is now devised, based on an a priori assumption on the velocity profile. The starting point is the mass conservation equation for the solid phase:

$$\begin{aligned} \frac{\partial {\langle \rho _s\rangle }}{\partial t}+{\nabla \cdot \langle \rho _s\varvec{{u}}_s\rangle }= -{\langle \dot{\omega }^{\text {het}}\rangle }-{\langle \dot{\omega }^{\text {pyro}}\rangle }, \end{aligned}$$
(21)

where \({\langle \rho _s\rangle }\) is the average density of the solid phase, connected to the intrinsic density \({\langle \rho _s\rangle }_s\) (assumed to be constant) through the solid volume fraction \(\epsilon _s\):

$$\begin{aligned} {\langle \rho _s\rangle }=\epsilon _s {\langle \rho _s\rangle }_s. \end{aligned}$$
(22)

In the current model of argo, the solid matrix is considered as rigid and stationary so that the convective term is equal to zero. Actually, a velocity for the solid phase must be now defined to treat the swelling mechanism. For this reason, the chemical production terms can be neglected, to focus on the convective transport mechanism, which is what actually needs to be modeled:

$$\begin{aligned} \frac{\partial {\langle \rho _s\rangle }}{\partial t}+\underbrace{\nabla \cdot \langle \rho _s\varvec{{u}}_s\rangle }_{\text {Convective term}}= 0. \end{aligned}$$
(23)

Normalizing \({\langle \rho _s\rangle }\) by the nominal value:

$$\begin{aligned} U = \frac{\langle \rho _s \rangle }{[{\langle \rho _s \rangle }]_n}, \end{aligned}$$
(24)

Eq. (23) can be rewritten as

$$\begin{aligned} \frac{\partial U}{\partial t}+\nabla \cdot (U\varvec{{u}}_s) = 0. \end{aligned}$$
(25)

Equation (25) is an advection equation describing the transport of the variable U (normalized average solid density), operated by a flow moving at the transport velocity \(\varvec{{u}}_s = (u_s , v_s, w_s)\). For simplicity, the assumption of one dimensional flow in the y-direction is adopted, which leads to

$$\begin{aligned} \frac{\partial U}{\partial t}+U\frac{\partial v_s}{\partial y}+v_s\frac{\partial U}{\partial y}=0. \end{aligned}$$
(26)

The boundary conditions are a consequence of the normalization, since U may vary between 0 and 1:

$$\begin{aligned} \left\{ \begin{aligned}&y=0 \quad \quad \longrightarrow \quad U(0,t)=1 \\&y=2L_i \quad \longrightarrow \quad U(2L_i,t)=0 \end{aligned} \right. , \end{aligned}$$
(27)

where \(L_i\) is the initial length of the porous material. Adopting the same philosophy of argo, the initial condition has to describe the transition from a pure fluid region to a porous medium, as sketched in Fig. 5. Furthermore, the interface should be enough smoothed to prevent the formation of a discontinuity. For these reasons, the initial condition can be expressed through a hyperbolic tangent function:

$$\begin{aligned} U(y,t=0) = \frac{1}{2}[1-\tanh {(y-L_i)}]. \end{aligned}$$
(28)
Fig. 5
figure 5

Sketch of the initial condition, in analogy with the current model in argo

Full size image

The swelling velocity \(v_s\) was modeled by physical insights: a positive velocity gradient should be imposed at the interface (where the heat load triggers the swelling mechanism) between the porous medium and the pure fluid region, as sketched in Fig. 6. During swelling phenomenon, the region close to the interface on the side of the gas will see an increase in \({\langle \rho _s \rangle }\), due to the injection of solid mass where an instant before there was a pure fluid. At the same time, on the other side of the interface, \({\langle \rho _s \rangle }\) has to decrease because the solid mass has been convected over a bigger volume. This method also solves the issue highlighted by Martinez [30]: the solid mass conservation is guaranteed, since the area under the curve (volume integral of density) does not change in time.

Fig. 6
figure 6

Velocity profile imposed to model the swelling mechanism and ensuring the solid mass conservation. U is the normalized average solid density, \(L_i\) is the initial length of the porous medium and \(v_s\) is the swelling velocity, normalized by a mean value \(\bar{v}_s\) and modeled using a sigmoid function S(y)

Full size image

The velocity gradient was modeled using a sigmoid function:

$$\begin{aligned} S(y)=\frac{1}{1+e^{(L_i-y)}}. \end{aligned}$$
(29)

Moreover, considering that the swelling mechanism consists in a thermal expansion, it is expected to automatically stop when the temperature gradients decrease below a minimum value. To evaluate the effect of thermal gradients, the 1D heat equation can be solved, as a first approximation, for the virgin material (denoted with the subscript v):

$$\begin{aligned} \frac{\partial T_v}{\partial t}= \frac{k_v}{\rho _v c_v} \frac{\partial ^2 T_v}{\partial y_v^2} , \end{aligned}$$
(30)

where \(k_v\), \(\rho _v\) and \(c_v\) are the thermal conductivity, density and specific heat capacity of the virgin material, respectively. For the purpose of reproducing the test in the VKI Plasmatron facility performed by Sakraker [8], the boundary conditions can be defined as follows:

$$\begin{aligned} \left\{ \begin{aligned}&y=0 \quad \quad \ \longrightarrow \quad k_v \frac{\partial T_v}{\partial y_v}=0 \\&y=L_i \quad \quad \longrightarrow \quad k_v \frac{\partial T_v}{\partial y_v}=\dot{q}_{\text {ext}}-\varepsilon _v \sigma T_w^4 \end{aligned} \right. , \end{aligned}$$
(31)

where \(\varepsilon _v\) is the emissivity of the virgin material, \(\dot{q}_{\text {ext}}\) is the external heat flux, \(\sigma\) is the Stefan–Boltzmann constant and \(T_w\) is the wall temperature.

Assuming a linear thermal expansion, the general definition for the expansion coefficient \(\alpha\) is given by

$$\begin{aligned} \alpha =\frac{1}{L}\frac{\mathrm {d}L}{\mathrm {d}T}. \end{aligned}$$
(32)

The local strain \(\epsilon\) is defined as

$$\begin{aligned} \epsilon =\frac{\mathrm {d}L}{L}=\alpha \ \mathrm {d}T. \end{aligned}$$
(33)

A relation between the strain and the displacement also exists:

$$\begin{aligned} \epsilon =\frac{\mathrm {d}s}{\mathrm {d}y}. \end{aligned}$$
(34)

The displacement field can thus be found as:

$$\begin{aligned} s=\int _{0}^{L}{\epsilon \ \mathrm {d}y}=\int _{0}^{L}{\alpha \ \mathrm {d}T\ \mathrm {d}y}. \end{aligned}$$
(35)

In an evolution problem, s and T are function of time too. Therefore, computing the time derivative and assuming \(\alpha\) to be constant, it is possible to define a velocity related to the effect of thermal gradients:

$$\begin{aligned} \hat{v}_s(t)=\frac{\partial s}{\partial t}=\alpha \int _{0}^{L}{\frac{\partial T}{\partial t}\ \mathrm {d}y}, \end{aligned}$$
(36)

where the temperature gradient is computed solving the 1D heat Eq. (30). Hence, the final definition for the swelling velocity is the following:

$$\begin{aligned} v_s(y,t)=\hat{v}_s(t)S(y). \end{aligned}$$
(37)

The spatial distribution of velocity is thus modeled by the sigmoid function S(y), whilst its evolution in time is described in terms of a decreasing velocity, namely the strain rate \(\hat{v}_s(t)\), which is driven by the temporal variation of thermal gradients. Therefore, the swelling mechanism automatically stops as \(\hat{v}_s(t)\rightarrow 0\) or, in other terms, when \(\partial T/\partial t \rightarrow 0\).

In argo, when pyrolysis is included, the local decomposition state of the material is taken into account, by means of the progress variable \(\xi\) introduced in Eq. (15). The virgin layer is denoted with \(\xi =0\), while the totally charred region is identified by \(\xi =1\). The transitional zone, i.e. the pyrolysis layer, is characterized by \(0<\xi <1\). The same philosophy was thought for the current physical model, to increase the degree of compatibility with argo. In this case, the only available parameter capable of reflecting the decomposition state of the material is the local temperature. Therefore, a pyrolysis temperature \(T_p\) is used to locate the border (\(\xi =0\)) between the virgin zone and the pyrolysis layer, while a char temperature \(T_c\) is chosen to identify the edge (\(\xi =1\)) between the pyrolysis layer and the totally charred zone, as shown in Fig. 7.

Fig. 7
figure 7

Two characteristic temperatures are tracked to locate pyrolysis and char fronts

Full size image

Both pyrolysis and char fronts are expected to travel along the material. Hence, the velocity profile defined by Eq. (37) is shifted down at each time step to track the pyrolysis front. Furthermore, since the pyrolysis front is expected to move faster than the char front, the pyrolysis layer will see an increase in its thickness \(\varDelta y_{\xi _{1,0}}(t)=y_{\xi =1}(t)-y_{\xi =0}(t)>0\). The sigmoid function S(y) was thus manipulated to change its slope, i.e. smoothing the velocity gradient at the interface to simulate the increase in thickness of the pyrolysis layer. The final definition for the swelling velocity is

$$\begin{aligned} v_s(y,t)=\hat{v}_s(t)\frac{1}{1+e^{\{(L_i-y)-[L_i-y_{\xi =0}(t)] \}/\varDelta y_{\xi _{1,0}}(t)}}. \end{aligned}$$
(38)

All these aspects will be clarified in Sect. 3.3 by analyzing the results provided by the matlab simulations, in which Eqs. (26) and (30) are numerically solved by means of a Finite Difference Method (FDM).

3 Numerical Simulations

In this section, the results of numerical simulations are presented, serving a dual purpose of testing the new routine implemented within argo for the computation of pyrolysis gases at equilibrium (Sects. 3.1 and 3.2) and analyzing the physical model developed for the simulation of swelling materials (Sect. 3.3). Hence, a first series of test cases and ablation simulations were performed by means of argo, followed by a simulation of the swelling mechanism coded in matlab.

3.1 Adiabatic 0D Reactor: Pyrolysis of TACOT

A first simple test case was studied by means of the ReactorZeroD solver of argo, to verify the new implemented tool: only the evolution of the species is solved, assuming adiabatic conditions, no convection and no diffusion [3]. Therefore, the only heat source comes from pyrolysis. An unsteady simulation was performed, using an explicit scheme for the temporal discretization and a time step equal to \(\varDelta t=10^{-4}\) s. A total time of 0.1 seconds was simulated, since a preliminary analysis showed that is sufficient to reach the steady state.

Fig. 8
figure 8

Adiabatic 0D reactor: domain of computation (left) and mesh (right)

Full size image

The domain of computation is a square containing the porous medium, discretized into 9 square elements (Fig. 8) and all the boundaries are treated as adiabatic walls. As regards the solid phase, the TACOT [27,28,29] material was simulated, that is a fictitious TPM created from literature data to mimic low-density carbon-phenolic charring ablators, such as PICA.

TACOT is characterized by a virgin density of 280 kg m\(^{-3}\), with a porosity equal to 0.8. The permeability starts from \(1.60\cdot 10^{-11}\) m\(^2\) and it evolves with porosity according to the Carman–Kozeny model. The tortuosity of the virgin material is equal to 1.2, while the initial radius of the carbon fibers is \(r_0=5\ \mu\)m. As regards the thermal properties, heat capacity and thermal conductivity are fitted as functions of temperature using the NASA-9 polynomial interpolation and they are shown in Fig. 9 for the virgin and charred materials.

Fig. 9
figure 9

Thermal properties of TACOT, expressed as a function of temperature

Full size image

For the fluid phase, a list of seven species was considered: \({\mathrm {CO}_2}\), \(\mathrm {CO}\), \(\mathrm {C}_6\mathrm {H}_6\), \(\mathrm {C}_6\mathrm {H}_5\mathrm {OH}\), \(\mathrm {CH}_4\), \(\mathrm {H}_2\mathrm {O}\), \(\mathrm {H}_2\). The thermal degradation of two fictitious compounds is described by means of an Arrhenius type law, expressed by Eq. (14). The coefficients are listed in Table 1.

Table 1 Arrhenius law coefficients for the description of pyrolysis
Full size table
Table 2 Elemental composition of pyrolysis gases
Full size table

As initial condition, a uniform field was set, with an initial pressure of 101, 325 Pa and a temperature of 1500 K, that is enough high to activate pyrolysis. Furthermore, the chemical composition of the mixture was initialized at thermochemical equilibrium, computed by mutation++.

Two simulations were performed: in the first one, a pre-fixed composition was set for the pyrolysis gas while, in the second one, the new implemented routine was tested calling mutation++ to compute the pyrolysis gas composition at equilibrium conditions, starting from its elemental composition specified in Table 2. A probe was located in the middle of the domain, as shown in Fig. 8, to track the time evolution of the quantities. The results are plotted in Figs. 10 and 11.

Fig. 10
figure 10

Results of the pyrolysis of TACOT, simulated by means of the adiabatic 0D reactor solver

Full size image
Fig. 11
figure 11

Comparison between pre-fixed and equilibrium mole fractions of each chemical species, during pyrolysis of TACOT

Full size image

The comparison shows that the main difference is in terms of temperature: the pre-fixed composition produced an underestimation of the temperature reached at the steady state. Another interesting result is in the discrepancy of chemical composition of the mixture in terms of species mole fractions, as can be observed in Fig. 11, where the main chemical species are shown. As expected, the new routine allowed to compute the composition of pyrolysis gases on the basis of local temperature and pressure (at equilibrium) rather than fixing the same composition for the whole simulation. Therefore, this is a more reasonable way of treating the production of pyrolysis gases and represents a further step towards the improvement of the numerical simulations of charring ablators.

3.2 Charring Ablator in Plasmatron Conditions

The previous test case was studied through a simplified solver, neglecting convection and diffusion and analyzing only the thermal decomposition. To include all the transport phenomena, a simulation was performed using the Navier–Stokes solver of argo to study ablation of a charring TPM in Plasmatron conditions. Due to the unavailability of data of cork-based ablators and considering also that only carbon-based materials can be treated at the moment in argo, the TACOT material was again selected. Moreover, considering that the inclusion of pyrolysis phenomenon implies the resolution of a stiff problem, the usage of extremely small time steps results in a very high computational cost. Therefore, a total time of 1 s was simulated (through an implicit time discretization), which is enough large to study the thermal decomposition but it is not sufficient to reach the quasi-steady state in terms of material recession. A sketch of the simulation is illustrated in Fig. 12.

Fig. 12
figure 12

Scheme of the simulation of TACOT in Plasmatron conditions

Full size image

The domain of computation is shown in Fig. 13. The hemispherical sample has a diameter equal to 25 mm and it is located at a distance of 15 cm from the subsonic inlet. According to Schrooyen et al. [25], a previous analysis had proved that just 13 cm are sufficient to correctly solve the flow field. The slip wall is far enough too, to avoid the blockage effect. Finally, the adiabatic walls of the holder extend to 25 mm from the sample up to the subsonic outlet.

The mesh consists of 4925 nodes and 6003 elements. A 1st order Lagrangian polynomial interpolation (\(p=1\)) is used inside each element, so that a second order of accuracy (\(p+1\)) is investigated using DGM. The computational grid is shown in Fig. 13 and the boundary conditions are listed in Table 3.

Fig. 13
figure 13

Computational grid and boundary conditions

Full size image
Table 3 Boundary conditions
Full size table

The elemental composition of pyrolysis gases is in Table 4. It was estimated for cork P50 through a statistical survey based on literature data and proposed by Başkaya [37].

Table 4 Elemental composition of pyrolysis gases, for cork P50
Full size table

A total amount of 11 chemical species was included: \(\mathrm {N}\), \(\mathrm {O}\), \(\mathrm {NO}\), \(\mathrm {N}_2\), \(\mathrm {O}_2\), \(\mathrm {CH}_4\), \(\mathrm {CO}\), \(\mathrm {CO}_2\), \(\mathrm {H}_2\), \(\mathrm {H}_2\mathrm {O}\), \(\mathrm {OH}\). Once produced, some of these species are frozen, while \(\mathrm {CO}\), \(\mathrm {CO}_2\), \(\mathrm {O}\) and \(\mathrm {O}_2\) are able to react with oxygen, according to the homogeneous reactions shown in Table 5. In particular, the generation of \(\mathrm {CO}\) and \(\mathrm {CO}_2\) comes from oxidation, pyrolysis and the homogeneous reaction too. In any case, all the chemical species are able to diffuse according to a Schmidt number \(\text {Sc}=1\).

Table 5 Homogeneous reactions included in the reaction mechanisms database of mutation++
Full size table
Table 6 Heterogeneous reactions included in the input file of argo to describe the oxidation of the carbon fibers
Full size table

As regards oxidation reactions, they are listed in Table 6. Their backward reaction rates are so small that the reverse reactions do not need to be considered [38]. Moreover, in TACOT material the carbon fibers are coated by char, therefore they begin to undergo oxidation only once the char has been totally removed. In addition, the charred material is able to react faster than the carbon fibers, therefore a factor 10 was applied to the pre-exponential coefficient A of char. The physical explanation behind this behaviour lies in the structure of the char layer: its cracks and defects make the charred zone more vulnerable to the attack of oxygen, so that the chain of carbon undergoes a faster reaction.

Concerning pyrolysis, two decomposition reactions were taken into account. The coefficients of the Arrhenius type law are listed in Table 7 and they were computed by Sakraker [8] for the cork P50, by means of a TGA analysis.

Table 7 Arrhenius law coefficients for the description of pyrolysis (data from Sakraker [8])
Full size table

The evolution of the species mass fractions along the stagnation line can be observed in Fig. 14. The initial composition was computed by mutation++ at equilibrium (Fig. 14a). At \(t=0.005\) s, traces of \(\mathrm {CO}\), associated to oxidation reactions, are detected at the interface (Fig. 14b). After \(t=0.5\) s, the production of several species can be observed (Fig. 14c), so this is an indication that pyrolysis has started and a thermal decomposition is affecting the porous material from the inside. The gas production especially involves \(\mathrm {H}_2\mathrm {O}\), \(\mathrm {H}_2\), \(\mathrm {CO}_2\) and \(\mathrm {CO}\), accompanied by very small trace amounts of \(\mathrm {CH}_4\) and \(\mathrm {OH}\). At \(t=1.0\) s (Fig. 14d) even the deepest layers of the material show the presence of pyrolysis gases, also because of convection and diffusion mechanisms. Moreover, the chemical boundary layer is clearly changing too.

Fig. 14
figure 14

Evolution of the species mass fractions along the stagnation line

Full size image

Figure 15 shows the mass loss due to both oxidation and pyrolysis. A mass loss of 1.2% was registered after 1 s, corresponding to a loss of 0.28 grams and a mass loss rate equal to 280 mg/s.

Fig. 15
figure 15

Mass loss due to oxidation and pyrolysis

Full size image

The thermal degradation of the phenolic resin can be analyzed in Fig. 16. The full profile is given by the sum of the density of each solid compound, i.e. carbon fibers (160 kg/m\(^3\)), two resins (40 kg/m\(^3\) each) and char (40 kg/m\(^3\)). After 1 s, the presence close to the interface of a point where the tangent line is horizontal means that the phenolic resin is almost completely decomposed there. The same observation can be clearly derived from Fig. 17, where the density contour of the two resin compounds is compared with a picture of a P50 sample taken by Sakraker [8]. Naturally, a sufficiently long simulation would provide results closer to the experiments.

Fig. 16
figure 16

Solid density profile along the stagnation line, as sum of the contributions of each compound

Full size image
Fig. 17
figure 17

Decomposition of the two resin compounds, compared with a P50 sample tested in the VKI Plasmatron facility

Full size image

Figure 18 shows the axial velocity along the stagnation line after one second. The negative velocity close to the gas-surface interface reached an absolute value of 10 m/s, that is considerably high and attributable to the severe blowing effect, which requires longer periods before disappearing. Finally, the maximum velocity computed at \(t=1.0\) s within the porous medium is approximately equal to 0.4 m/s (Fig. 19).

Fig. 18
figure 18

Axial velocity along the stagnation line, after \(t=1.0\) s

Full size image
Fig. 19
figure 19

Temperature and velocity fields at \(t=1.0\) s

Full size image

3.3 Swelling

The development of a matlab code based on the FDM allowed to test the physical model presented in Sect. 2.4. A one-dimensional domain was first considered, extending along the y-direction, up to twice the initial length of the sample, \(L_i\). The computational grid consists of 201 nodes and a time step equal to 5e-4 seconds was set, to satisfy the Courant–Friedrichs–Lewy (CFL) condition. A forward Euler explicit scheme is indeed used for the time discretization.

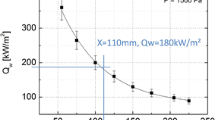
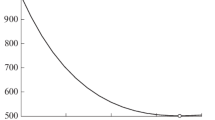
The model devised to simulate the thermal expansion is based on an appropriate (a priori) definition for the swelling velocity profile, \(v_s\). A sigmoid function is used to define the spatial distribution of \(v_s\). This approach allows to conserve the solid mass, as shown in Fig. 25a, where the area under the curve does not change with time. The mass conservation is indeed evaluated at each time step (Fig. 25c) by computing an approximation of the integral of U through the Simpson’s quadrature rule. As expressed by Eq. (37), the sigmoid function is also multiplied by a strain-rate \(\hat{v}_s(t)\), to make \(v_s\) a function of time too. In fact, the swelling velocity is expected to vanish as the thermal gradients drop sufficiently. For this reason, the 1D heat equation was solved (Fig. 20): starting from an initial condition of 298 K, a heat flux \(\dot{q}_{\text {ext}}= 251.77\) kW/m\(^2\) was imposed at a boundary, to reproduce the experiment performed by Sakraker [8] in the VKI Plasmatron facility and a wall temperature \(T_w=1560.51\) K was computed. Hence, the strain-rate \(\hat{v}_s(t)\) is obtained from Eq. (36): its decrease over time is driven by thermal gradients (Fig. 22). As a result, the \(v_s\) profile decreases with time too, governed by the evolution of temperature gradients, until it collapses on the straight line \(v_s(y,t)=0\), as shown in Fig. 21. This provides a relation between the swelling mechanism and the temperature field, so that the thermal expansion is free to automatically stop as the temperature gradients become small enough (Fig. 22).

Fig. 20
figure 20

Solution of the 1D heat equation in Plasmatron conditions. Pyrolysis and char fronts are tracked by means of two characteristic values of temperature

Full size image
Fig. 21
figure 21

The velocity profile is shifted at each time step, governed by the evolution of thermal gradients

Full size image
Fig. 22
figure 22

Evolution in time of the strain-rate \(\hat{v}_s\), governed by thermal gradients

Full size image

The effect of the decomposition state of the material was included too: during the resolution of the 1D heat equation, both pyrolysis and char fronts are tracked by means of two characteristic temperatures, provided by Sakraker [8], as shown in Fig. 20. The two fronts travel along the material at different velocities, so the thickness of the pyrolysis layer is expected to increase, as can be deduced from Fig. 23.

Fig. 23
figure 23

Modeling of the decomposition state of the material. Traveling at different velocities, pyrolysis (\(\xi =0\)) and char (\(\xi =1\)) fronts increase their distance along the length of the sample, which results in a greater thickness of the pyrolysis layer

Full size image

These effects were directly modeled in the expression of the swelling velocity and can be better understood looking at Fig. 24, where they are analyzed separately: the velocity profile \(v_s\) is shifted down at each time step to simulate the pyrolysis front consuming the virgin layer. At the same time, the slope of the velocity profile is increased at each step to simulate the increase in thickness of the pyrolysis layer. Both pyrolysis and char fronts (respectively, identified by \(\xi =0\) and \(\xi =1\)) indeed travel deep within the material increasing their distance, since the pyrolysis front is faster than the char front.

Finally, the various effects were combined together, getting the result given in Fig. 25a: as expected, during swelling the average solid density increases on the side of the gas and decreases on the side of the porous material, such that the solid mass is conserved.

Fig. 24
figure 24

Scheme of the further physical mechanisms which were modeled to increase the level of compatibility with argo

Full size image
Fig. 25
figure 25

Simulation of swelling on a 1D domain. A total time equal to 132 s was simulated, to reproduce the experiment of Sakraker [8]

Full size image

For a better visualization purpose, the same model was extended to a two-dimensional domain, although a zero velocity was imposed along the x-direction. The results of the final simulation are given in Fig. 26. Instead, Fig. 27a shows the evolution of some characteristic values of the U contour near the interface; the contour \(U=0.3\) evolves along the y-direction towards the external gas (Fig. 27b), while the contours \(U=0.5\) and \(U=0.7\) shift down along the material, proving that the solid mass has been spread on a bigger volume, as one would expect from an expansion mechanism. For these reasons, the developed model showed the capability to predict the swelling behavior and provide an answer to the question about how to model this physical phenomenon.

Fig. 26
figure 26

Simulation of swelling on a 2D domain

Full size image
Fig. 27
figure 27

Swelling: evolution of the U contour with time

Full size image

4 Conclusions

This work focused on the numerical modeling of a new class of cork-based ablative materials with thermal protection purposes. Their excellent mechanical and thermal properties make them appealing in the framework of atmospheric re-entry. At the same time, the atypical response of such materials requires further efforts and, for this reason, it is currently object of study by ablation community. Most of modern ablation simulation tools are indeed not capable of predicting ablation and swelling together, therefore some methodologies to treat both pyrolysis and thermal expansion of cork-phenolic ablators were explored and tested in this work.

Concerning pyrolysis, actually only carbon-phenolic ablators can be simulated in argo, so a further modeling effort is required to include the treatment of cork-phenolic ablators. However, the development of such a complex model was beyond the scope of this work. Hence, this paper focused on the improvement of the way in which the thermal decomposition is taken into account within argo, providing an accurate method to compute the pyrolysis production rate at thermochemical equilibrium, by implementing a function to call the VKI mutation++ library. The test case performed using the adiabatic 0D reactor solver of argo showed that the previous strategy, based on the pre-fixed composition, led to an underestimation of temperature due to pyrolysis of about 130 K. A simulation of a charring ablator was then performed through the Navier–Stokes solver. Data of TACOT were used, whereas the elemental composition of pyrolysis gases was estimated from literature. A total time of 1 s was simulated, which is enough large to study the thermal decomposition but not the material recession due to oxidation. For the future, it could be also interesting to repeat the analysis using a second-order Lagrangian polynomial interpolation (\(p=2\)), to take advantage of the high-order accuracy offered by the DG method. In the light of this, even though argo is not ready to treat cork-based ablators yet, the new implementation represents one more step to better simulate charring ablators.

As regards the physical model of swelling, a one dimensional model was developed, based on a 1D nonlinear advection equation and assuming a proper swelling velocity profile derived from physical insights. Great attention was reserved to ensure the mass conservation and the governing equation was also combined with the 1D heat equation, to take into account the effect of thermal gradients in the swelling phenomenon. Finally, the decomposition state of the material was considered too for the purpose of changing the velocity distribution along the material depending on the temperature evolution. However, it is also worth pointing out the simplified assumptions of the model, for future improvements. The hypothesis of one dimensional flow was necessary due to the lack of experimental evidences about swelling along the other directions, but the thermal expansion actually might imply an anisotropic response. Moreover, the heat equation was solved for the pure virgin material, as if its properties did not change during heating. Nevertheless, despite these simplifications, the physical model developed and tested in matlab revealed promising results and offered a better understanding of the swelling phenomenon, opening the way towards further developments. Since the results fulfilled expectations, the aim for the future is to implement this physical model within argo, to perform a complete simulation of a cork-phenolic ablator.