FEM Benchmark Problems for Cracks with Spring Boundary Conditions Under Antiplane Shear Loadings

Abstract

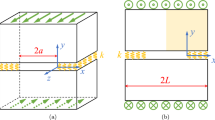
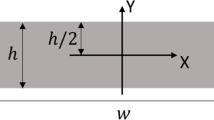
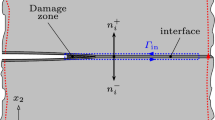
A new analytical solution in the form of asymptotic series is proposed and studied for Mode III crack problems with spring boundary conditions, which are, in the mathematically-oriented literature, referred to as Robin boundary conditions. Under the assumption of antiplane shear loading, the corresponding elastic problem reduces to the Laplace equation for the out-of-plane displacement. Numerical solutions for benchmark problems are obtained, applying the Finite Element Method, to verify this asymptotic approximation. In particular, two problems are studied, Neumann–Robin and Dirichlet–Robin. Both are used to define a partially damaged adhesive interface in which the Linear Elastic Interface Model is applied. The numerical solution is obtained using the software FEniCS, for which the variational formulation of the problem is developed. Then, it is compared to the analytical expressions proposed for the problem, computing a normalized error. Finally, a convergence analysis is presented. Several parameters, such as the stress singularity or another error measure, are used to analyse two different ways to refine the mesh.

Appendix

The recursive problems for obtaining N–R and D–R solutions are the following, for N–R

$$\begin{aligned} \varDelta u_{j}^{(k)}&= 0 \quad \text {in } \quad \varOmega , \end{aligned}$$

(36)

$$\begin{aligned} \quad \frac{\partial u_{j}^{(k)}}{\partial \theta }&=0 \quad \text {on } \quad \varGamma _{{\text {N}}}, \end{aligned}$$

(37)

$$\begin{aligned} \frac{1}{r}\frac{\partial u_{j}^{(k)}}{\partial \theta }&=-\gamma u_{j}^{(k-1)} \quad \text {on } \quad \varGamma _{{\text {R}}}. \end{aligned}$$

(38)

whereas for the D–R

$$\begin{aligned} \varDelta u_{j}^{(k)}&= 0 \quad \text {in } \quad \varOmega , \end{aligned}$$

(39)

$$\begin{aligned} \quad u_{j}^{(k)}&=0 \quad \text {on } \quad \varGamma _{{\text {D}}}, \end{aligned}$$

(40)

$$\begin{aligned} \frac{1}{r}\frac{\partial u_{j}^{(k)}}{\partial \theta }&=-\gamma u_{j}^{(k-1)} \quad \text {on } \quad \varGamma _{{\text {R}}}. \end{aligned}$$

(41)