Abstract
By accelerating the overcoming of space on certain relations, transport systems alter the accessibility of places and distort geographical time–space. Particularly in the case of discontinuous and tiered transport systems such as (high-speed) rail networks, effects on time–space can be highly selective and difficult to visualise. This paper compares different methods of operationalisation and visualisation of the effects of new transport systems (infrastructures and services) on time–space, and examines their strengths and weaknesses, using the example of the evolution of the German rail network between 1990 and 2020. The methods are well-known ones such as isochrones, choropleths using measures from network theory, anamorphosis (cartograms) and less-known ones as spring maps and the shrivelling model. For the examination of the readability of the methods, we present relevant properties for time–space maps. The results suggest that conventional methods are simpler to interpret, but fail to convey certain properties, while less frequently used methods may be better at incorporating the properties at the cost of being more difficult to read.
Zusammenfassung
Durch die Beschleunigung der Raumüberwindung auf konkreten Relationen können Transportsysteme die Erreichbarkeit von Orten und somit insgesamt das geografische Raum-Zeit-Gefüge verändern. Insbesondere im Falle hierarchischer und unstetiger Transportsysteme wie Hochgeschwindigkeitsbahnnetze sind Effekte auf das Raum-Zeit-Gefüge oftmals trennscharf und somit herausfordernd für deren Visualisierung. Die vorliegende Studie vergleicht verschiedene Methoden der Operationalisierung und Visualisierung von durch Veränderungen in der Infrastruktur oder im Betrieb von Transportsystemen ausgelösten Effekten auf das Raum-Zeit-Gefüge. Die Stärken und Schwächen der Methoden werden anhand des Beispiels der Entwicklung des deutschen Eisenbahnnetzwerks zwischen 1990 und 2020 untersucht und beleuchtet. Unter den Methoden sind bewährte Ansätze wie Isochronen, netzwerktheoretische Maße visualisierende Choroplethenkarten, Anamorphosen (Kartogramme), sowie weniger bekannte wie Federkarten (Spring Maps) oder Schrumpfkarten (Shrivelling Maps). Wir präsentieren relevante Eigenschaften für die Untersuchung der Lesbarkeit von Raum-Zeit-Karten. Die Ergebnisse vermitteln, dass konventionelle Methoden zwar leichter zu interpretieren sind, aber wichtige Eigenschaften nicht darstellen können. Seltener genutzte Methoden setzen die Eigenschaften in der Visualisierung besser um, sind allerdings schwieriger zu lesen.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Distances in space can be covered at different speeds, depending particularly on the presence of transport infrastructures and services. The physical, and geographical distances between places and their actual or perceived distances in time differ. These differences and their accelerating development have long led to thinking about creative cartographic solutions that visualise the time-based proximity between places and reveal their accessibility.
Recent innovations in transport technology have again altered the dynamics of differential distortions of time–space geography. Particularly, the development of high-speed rail (HSR) systems in the last decades mainly throughout Asia and Europe has transformed temporal proximities by land-based transport systems, by dramatically and abruptly reducing travel times on selected origin–destination pairs. At the same time, travel times between regions not connected to the new transport system remained stable or even increased, as other rail services were sometimes discontinued. However, often-used cartographic renderings of travel-time effects, like isochrone maps or anamorphoses, do not always show these differential effects on varying scales. In this paper, we undertake a comparison of a range of methods of visualisation of the structure and dynamics of such time-spatial geographies, using the evolution of the German rail network in the last decades as a case study.
The paper is structured as follows: after the theoretical background, we introduce our case study and five types of maps usable for time–space effects of transport infrastructure systems: isochrone maps, choropleth maps using accessibility indicators such as closeness centrality, anamorphoses, spring maps, and the shrivelling map. First, we describe the methodical background for each visualisation type, followed by an application of the methods using our case study. We then systematically compare the techniques in the evaluation section, before concluding.
2 Theoretical Background
A mode of transport that allows one to travel with almost equal speed in all directions and between all places, with no need for heavy infrastructure, e.g. walking, does not distort geographical time–space. Physical and time-based distances are identical. However, from early times on, waterways and highways served as a means to cover certain relations faster than others. The nineteenth century brought the development of precise topographic maps on the one hand, but also the emergence of new modes of travelling such as rail and steamship, which led to a shrinking world (Janelle 1973), that is, an ever-increasing distortion of geographical time–space as part of globalisation. The visualisation of such shifts within time–space geography is of particular interest. However, this shrinking process occurs unevenly across space (Knowles 2006): on certain relations, travel times are reduced drastically, while travel times in other relations remain unchanged or even increase. Place A and B along such transport routes can be closer to each other in temporal-relational terms than A and C offside them, although the geographical distance between A and C may be shorter (L’Hostis 2016). The result is a new landscape of proximities and peripheries, of accessibility and inaccessibility, that differs from the conventional cartographic representations of space we know and requires innovative approaches to visualisation. Such visualisations may reveal more than just the convenience a certain transport system provides: inherently, they can shed light on power relations in a world system (Friedman 1986; Sassen 1994) that increasingly relies on flows between dominant nodes (Castells 1996).
The task to map this nexus has occupied geography not only since the discovery of the category "time" for the subject (Hägerstrand 1970). Among the most widespread attempts for visualisation are isochrone maps, anamorphoses, and accessibility maps, which were all already in use in the nineteenth century (Letaconnoux 1907). Recently, GIScience has simplified the rendering of such visualisations, and made new visualisation techniques possible, such as shrivelling maps. However, a number of particularities make the task a challenging one, inter alia:
-
Both complex indicators and unconventional cartographic techniques can aggravate readability and interpretability, particularly for lay users,
-
the spatially selective nature of time–space compression typically requires more than two dimensions for precise mapping,
-
spatial inversion can occur, in the sense that a significant detour, involving a sequence in the opposite direction, can be faster than a direct route (Tobler 1961; Bunge 1962)
L’Hostis and Abdou (2021) argue that methods for the production of cartographic time–space maps can be subdivided into two categories: (a) methods where points are moved, and (b) those where edges are drawn in a special way.Footnote 1 We extend this categorisation by a third group, in which (c) points or surfaces are drawn in a way that accounts for their accessibility.
In the following, we compare five visualisation techniques: isochrone maps using surfaces, choropleth maps using closeness centrality as an indicator (usually done by colouring the areas of administrative boundaries, i.e. surfaces), anamorphoses (points are moved), spring maps (edges drawn in a special way), and the shrivelling model (three-dimensional surfaces).
The evaluation of, explicitly, time–space maps, according to L’Hostis and Abdou (2021), needs to incorporate four properties of time–space. The first property relates to the acceleration of speeds after the introduction of new transport means on certain transport links that lead to geographical time–space shrinkage. This property allows us to compare two states of the network over time. The second property examines whether maps display the transport networks on which alterations of time–space occur. Thus, this property makes intelligible the reasons why a change in time–space appeared, that is on which components of the transport infrastructure the acceleration of speeds takes place. The third property deals with the challenge of the simultaneous depiction of multiple co-existing transport modes that are each characterised by different speeds. This refers to the trade-off between presenting all transport connections or only those of higher hierarchy (fast connections). Omission of too many lower-hierarchy (slow) connections bears the risk of rendering biased or incomprehensible representations. The fourth property is associated with spatial inversion (Tobler 1961; Bunge 1962), which deals with those connections that first go in the opposite direction to reach a distant destination. This is directly related to the third property because often passengers have to reach a high-speed transport means with a slower local or regional transport mode, which leads to actual physical detours in space. Finally, we synthesize these four properties into a fifth overall property “readability” to theoretically assess the overall readability and intepretability of time–space maps. Table 1 summarises the five properties. Other earlier studies provide further considerations as regards time–space visualisations (Avelar and Hurni 2006; Ahmed and Miller 2007; Ficzere et al. 2014; Wu et al. 2020).
The assessment of the readability or usability of cartographic visualisations is a contentious point (Field and Demaj 2012). There are criteria, such as famous Bertin’s semiology (1983), that guide cartographers, as well as laypersons, applying easy-to-use software today, on how to create high-quality maps, which is the task that constitutes the core of the art of cartography (Mackinlay 1986; Harvey and Losang 2019; MacEachren 2019; Brath and Banissi 2019; Morita 2019). To validate whether maps resulting from the application of the guiding criteria actually convey the intended cartographic message, researchers have developed methods that evaluate the quality of maps outside the realm of the map-maker’s own subjective judgement. Three broad categories of such map evaluation designs should be mentioned. Although all three categories are concerned with the evaluation of the readability of a map, they all serve different tasks and are complements rather than substitutes for each other.
First, expert cartographic assessments are one way of improving maps as experts are trained in the field and can give valuable feedback. However, maps are often designed for non-cartographer users, who, without formal training, may analyse maps from different perspectives. Therefore, this approach is more catered to the exploratory, stimulating and idea-generating exchange between cartographers at more fundamental levels of research. In later stages of the research process, other evaluation designs have higher chances to produce constructive evaluative feedback.
The second map evaluation design category involves all approaches that can be subsumed under the term user studies. Within cartographic contexts, user studies aim at generating insights about (lay) map users’ understanding and interpretation of maps, while for psychological or cognitive researchers, user studies about maps allow them to reconstruct the brain’s processing of visual information absorption (Roth et al. 2017). User studies have various design options as they could be conducted in or outside of laboratories, as well as be of qualitative or quantitative kind. Possible methods include interviews, questionnaires, surveys, focus group discussions, inter alia (Schiewe 2022). One of the most popular methods is called eye-tracking, which, with the help of machines, records the test person’s eye movements across a projected map (Krassanakis and Cybulski 2019, 2021; Fairbairn and Hepburn 2023). The tracked eye movements facilitate inferences on the map content, i.e. where salient or unobtrusive features are located; as well as the eye itinerary across the map, which helps to establish a map user’s train of thought. Subsequently, the information obtained lets map-makers evaluate whether their map design effectuated the intended map-reading behaviour. Eye-tracking is associated with the risk of the inability to generate external validity for especially two reasons. On the one hand, test persons in the user studies are often university students who are not representative of the target audiences of some particular maps. On the other hand, a user study is not a real-world scenario, which introduces biases in the estimation of how map users read and interpret maps. Careful design of the user study is therefore indispensable.
While the first two map evaluation designs are based on human assessments, the third one rests on principles of computational utomatization. The main idea is to devise a set of statistical properties according to which a map-generating algorithm computes and draws map features. This evaluation design stems from the map generalisation literature, which focuses on developing schematised and simplified maps that abstract from highly detailed reality while still remaining legible (Stigmar and Harrie 2011; Stoter et al. 2014; Touya et al. 2016; Raposo et al. 2020; Cheng et al. 2021). A comprehensive survey on the state of the art in map generalisation by Hogräfer et al. (2020) gives valuable insights into the schematization of maps. The trade-off is to display as much information as possible without producing clutter, which would inhibit a map’s legibility. Clutter arises when an excessive amount of disorganized information appears on a map (Touya et al. 2016).
For this study, we use the expert evaluation design by synchronising the distinct assessments of the three authors. As the intention of this study is to provide a collection and discussion of fundamental time–space mapping techniques, expert evaluations are the appropriate design choice.
3 Materials and Methods
In this section, we first briefly introduce the evolution of German rail time–space and our used materials. Then, we present different time–space mapping techniques and provide applications to our data set, and finally, give short assessments of the applications.
3.1 Materials: Evolution of Rail Time–Space in Germany
While a common European HSR network is slowly emerging, up to now, rail infrastructure development has remained largely a national affair in the last 30 years. A plethora of studies exist on the accessibility effects of the pioneering network of France (L’Hostis 1996) and Japan (Shimizu 1992), and the fast-growing networks of Spain (Moyano et al. 2018) and China (Cao et al. 2013). However, the evolution of rail time–space in Germany has not been studied in detail in the last decades. This is unfortunate, as the German case is characterised by conditions that make a comparison with other countries worthwhile:
-
Germany is a polycentric country with a federal political system, which has led to a less radial and more grid-like, but also "patchy" implementation of HSR.
-
Due to the federal political system, the comparably high bargaining power of local and regional governments has led to the inclusion of more stations in smaller and mid-sized towns in the network.
-
The German HSR network is fully interconnected with the conventional network, such that HSR, intercity, regional as well as freight trains can and do interchangeably use conventional and most HS tracks.
-
The similar timing of the inauguration of the first HSR lines in June 1991 and the German reunification in October 1990 led to a double transformation of time–space.
Wenner and Thierstein (2020, 2021) analysed the spatial distribution of regional rail accessibility in Germany between 1990 and 2030 by measuring the potential accessibility of the population and degree centrality. Furthermore, Wenner and Moser (2020) show closeness centrality, betweenness centrality and daily accessibility, which are all displayed as choropleth maps. They also produce time–space analyses in the form of anamorphosis maps. These studies show that there have been a ‘shrinkage’ of time–space relations along the axes of HSR, but the effects of refurbishment and reconnection of the Eastern German rail network had far stronger overall effects. At the same time, with the abandonment of many regional and local connections, the periphery became disintegrated with the loss of long-distance connections. These results are in light with Spiekermann and Wegener (1994), who predict a shrinking of space across regions in overall but warn of precisely this kind of polarisation.
However, these studies have not yet harnessed the strengths of spring and shrivelling maps. A new synthesis of these methods and a more advanced version of the underlying data will help to understand the actual development of regional rail accessibility and the change in inter-regional travel times from 1990 to 2020 in Germany, as well as demonstrate the weaknesses and strengths of the various mapping methods.
For the analyses in this article, we constructed a rail network database for Germany and a 4-h buffer zone around the country by semi-automatically digitising historical and current timetable data. For the historical timetable, we used data provided by Grahnert (2020). The 2020 data was gathered from the website of the German rail operator, Deutsche Bahn, at the time of its application.
As a spatial base unit, we used the centres of functional city regions as defined by the German Federal Institute for Research on Building, Urban Affairs and Spatial Development (BBSR), and NUTS-3 regions in the buffer zone. When destination weights were used, these refer to the residing population.
3.2 Methods: Time–Space Mapping Techniques
Time–space mapping methods are associated with two different types of visualisations. The first one aims to visualise actual tracked movements of one or many individuals over time in space, which is often done using a time–space cube (Kraak 2003). These visualisations are beyond the scope of this paper. Instead, we want to visualise how differing speeds of transport means across different origin–destination pairs in a region, resulting in distinct travel times, shape the travel time distance relations of one, some or all points or areas to all others points or areas in the region. Time–space maps can be used for many different goals as they present techniques that communicate either:
-
how fast transport means can travel from an origin point to any other point (“Origin-Specificity”),
-
how (relatively) accessible a point or a region is compared to other points or regions (“Accessibility”),
-
what the underlying network structure for travel routes is (“Transport infrastructure”),
-
how fast connections between origin–destination pairs are compared to others (“Relative Distances”),
-
in what directions in which chronological and spatial order specific routes develop. (“Routing”, this resembles the time–space cube idea)
-
how the use of space distortion and thereby generated geographical discontinuities can increase awareness of differences in time–space relations in a map (“Continuity”)
-
how weighting of some features in the map can shift the map-reader’s visual impression, i.e. including population weights in an accessibility indicator. (“Weighting”)
Time–space thus subsumes a multitude of aspects related to transport networks. We chose the techniques portrayed in the following sections as they can be considered the most often used techniques (like isochrones, choropleth maps, and anamorphoses), which we extend with the adaptation of lesser-known ones (like spring maps and the shrivelling model), that are in overall capable of visualising the most relevant characteristics of geographical time–space.
Our innovation in this paper is to collect and display the most important characteristics of geographical time–space, explain what methods can be used to address the characteristics, show examples of applications and discuss their strengths and weaknesses.
3.2.1 Isochrone Maps
Isochrone maps are one of the oldest forms of representing travel times on a 2-dimensional map, with the first examples dating from the nineteenth century (Letaconnoux 1907). They show the area(s) one can reach within (a) certain time threshold(s) from a given starting point as "travel time budget indicator" (Schwarze 2005). The representation of the earth's surface remains topographic. Isochrone maps are relatively easy to comprehend, also due to their widespread use (O’Sullivan et al. 2000). However, a major limitation consists in the necessity to select a single reference location, increasing the effort for spatial and temporal comparisons.
The need to select an origin can be mitigated by overlapping the isochrones for a given time threshold on a map for a set of origins, which effectively highlights those places that are within the most isochrones of other locations. Such a process can be combined with the application of a time-geographical framework (Hägerstrand 1970), i.e. typical framework conditions of specific travel purposes, such as business travel for meetings. An application example would be a map that shows places that can be reached with a return journey during one day, with the condition that a certain number of hours is spent at the destination ("daily accessibility"). Such information can then be displayed point-wise, network wise (L’Hostis et al. 2017), or using regional areal choropleths, i.e. colours for differentiation.
3.2.1.1 Isochrone Maps from Frankfurt am Main
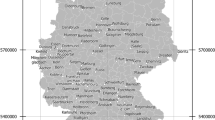
Figure 1 shows as isochrone maps the destinations that can be reached within certain time thresholds by rail, starting from Frankfurt am Main central station (as the busiest railway station in Germany by passenger numbers) on a typical weekday, for the years 1990 and 2020. Generally, an expansion of the reachable area, with less time needed, can be seen in most directions. The colours in the figure respond to the minutes needed to reach the areas, as indicated in the legend. The expansion is particularly articulated along the axes of HSR infrastructure that have been constructed radially around Frankfurt and the HSR line in France between Paris and Strasbourg that is also used for services from and to Frankfurt. Another marked change is the strong expansion eastwards, which corresponds to the refurbishment and reopening of conventional rail routes across the former inner-German border and between Germany and its eastern neighbours. Interestingly, little change can be observed towards the south, i.e. towards Switzerland and Italy.
Isochrone maps are relatively easy to interpret also for lay people, however, the necessity to select one origin location restricts its use for more complex analyses of entire networks and regarding inner peripheries. A challenge posed by isochrone maps is the degree of detail: are all locations that make up the areas between access points of long-distance transport means reachable? In Figs. 1a) and 1b), this is not always true. Instead, the method was chosen to convey the information on how far away transport technology allows passengers to travel. Technically, the isochrone maps in our use case should only colour the stations reachable within the respective time budgets to avoid assumptions about further transport possibilities to the hinterland of HSR stations. Isochrones are usually used in local contexts, where detailed mappings are the goal. We follow this approach also to discuss the features of this conventional method.
3.2.2 Choropleth Maps Using Closeness Centrality
Having their roots in urban and transport planning (Kansky 1963), complex accessibility indicators have been developed that can be used to visualise time–space compression. The simplest forms of accessibility indicators are counts per territorial unit, such as the number of stations, the length of track, or the number of departures or lines at a certain stop. Such simple indicators neglect the networked and differential effects of transport infrastructure systems. Advanced indicators are based on networks of nodes and edges, and consider travel time and destinations. In fact, isochrone maps can be considered as a special case of an accessibility map. Finally, complex accessibility indicators show, for all nodes in a given network, the cumulative effort necessary to reach (all or a defined set of) other nodes, i.e. 'Closeness Centrality'. The consideration of destination weights is an important difference from the other forms of visualisation presented in this article. In addition, the effort to reach destinations can be inversely weighted using functions (e.g. exponential or gaussian) together with the inclusion of a buffer zone (for a detailed description of accessibility measurements see Song (1996) and Geurs and van Wee (2004).
Other graph-theoretical measurements, such as betweenness and degree centrality, can also be employed as accessibility indicators. However, we do not include them in our comparison here, as we focus on travel times as the main factor of time–space compression rather than (non-)directness of connections between nodes.
For this paper, we employ a closeness centrality indicator with weighted nodes but unweighted travel times. Closeness centrality is usually denoted as an inverse value (Erath et al. 2009): the shorter the average travel time to all other regions, the higher the closeness centrality. We consider the non-inverse travel time to other nodes as easier to interpret and hence use the non-inverse values, which could be better termed as ‘farness’. Hence, lower values represent a shorter average travel time to all other regions and hence a higher accessibility level. The equation is expressed below in Eq. (1),
where \({W}_{j}\) is the weight of destination region j (residing population) and \({d}_{i,j}\) is the travel time between regions i and j by rail. As accessibility indicators typically yield values for single stations or areas, they can be displayed using point or area symbols (choropleths).
3.2.2.1 Choropleth Maps: Closeness Centrality of German Regions
Figure 2 shows the absolute closeness centrality values for German city regions for 1990 and 2020. Clearly visible is the bias towards centrally located regions like Hannover, which always exhibit shorter average travel times to other regions. However, Fig. 2b) shows that with new infrastructure development, cities further away from the core, like Frankfurt am Main, can also take a central position with regard to closeness. East Germany shows the largest aggregate improvements concerning closeness.
Choropleth maps have the advantage that they usually exhibit administrative regions that readers know and who are thus able to interpret the transmitted values of the mapped metric through the colouring scheme, especially in political and economic contexts with statistical variables such as income. However, they only present aggregated values by adding values of many smaller areas from the bottom up or just assign one value from the top down to all smaller parts of the region. They also neglect the visualisation of transport network characteristics, which in the context of time–space maps might be problematic.
3.2.3 Anamorphoses
Anamorphic maps, also called cartograms, use advanced computational methods of multidimensional scaling to rearrange a topographic network according to temporal distance in two-dimensional space, thereby creating 'distorted' maps. Consequentially, the resulting maps have a time scale instead of a distance scale. They are a vivid method to illustrate the effects of transport infrastructure, which is represented as a “shrinkage” of space (Spiekermann and Wegener 1994) and have been employed in geography early on (Tobler 1961; Bunge 1962). An exact representation of the time distances between all points would, however, require a higher-dimensional coordinate space. Thus, two-dimensional anamorphoses are always only approximate solutions. As a result, they can hide peripheral(ising) and unconnected areas, particularly when they are surrounded by other, well-connected areas (L’Hostis 1996; L’Hostis 2009). Acceleration is rendered by combining different maps in a single graphic, with usually the same time–space scale, as in Spiekermann and Wegener (1994). A detailed description on the mathematical background can be found in Spiekermann and Wegener (1993, 1994).
To generate time–space maps, we employed a non-metric multidimensional scaling algorithm coded in R. The non-distorted base map is premised on an equal speed of 60 km/h in all directions, the same as in Spiekermann and Wegener (1994), but using more nodes, with Frankfurt am Main as the map centre.
3.2.3.1 Anamorphoses of German Rail Time–Space
Figure 3 shows time-distance as a spatial distance by means of a map distortion. They allow comparing visually the temporal distance in the rail network with the actual topographical distance.
In 1990, the year of German reunification, particularly the strong differences in travel time between East and West become obvious, resulting mainly from the deterioration of the infrastructure in the former German Democratic Republic (GDR), and the lack of connections across the inner German border. The two economic systems have not only resulted in differences in economic productivity, but effectively in different spatio-temporal regimes and landscapes. This is already observed by Spiekermann and Wegener (1994) in their time–space maps of German rail accessibility. They highlight the particularly slow connections between Bavaria and the former GDR. But also in West Germany several “blobs” of remoteness become visible, i.e. to the south of Köln.
The change between 1990 and 2020 is most drastic with respect to the former inner-German border, which is hardly discernible anymore. The major metropolitan cores move closer together, hiding the fact that the space in between does not always participate in this development. Geographically peripheral regions with high travel times to the cores become visible as “spikes” that radiate outwards from the core area of high integration, i.e. the region northwest of Berlin in Fig. 3b). On the opposite, peripheral metropolitan cores that benefit from faster access generate "troughs" in the geographical shape, pointing inwards, that express the relative improvement of their accessibility, as is the case for Köln, Frankfurt am Main, München and Berlin.
3.2.4 Spring Maps
Spring map were invented independently at the same time in France and the USA (Plassard and Routhier 1987; Tobler 1997), despite Tobler publishing them ten years later. A spring map shows a transport network where locations remain fixed, while edges take the form of 'springs', i.e. 'zig-zag' lines. The visual length of the spring expresses the length of the edge measured empirically, usually in hours. Recent developments of the model explored the use of sinusoid curves (Buchin et al. 2014) instead of broken lines, to improve the readability. For the automatic generation of the sinusoid curves, we use the ratios of distance-to-time and time-to-distance for the amplitude and frequency of the curves. Higher frequencies and higher amplitudes represent worse transport infrastructures, that is, slower average speeds and longer travel times on a relation. The intuition is that an elastic spring with less total length is needed to cover a distance, thereby indicating efficiency.
3.2.4.1 Spring Maps of German Rail Network
Spring maps are more network diagrams than proper geographical space representations, using accurate topographic positions of cities as nodes and springs for the network edges connecting cities. This method allows for an analysis of the network edges properties and presents a creative alternative to a plain network depiction using colours for values of edge properties, i.e. travel times.
Figure 1 displays the most important major long-distance connections spanning Germany's rail network in 1990 and 2020. It shows in which relations the biggest travel time reductions have been facilitated between 1990 and 2020, with East Germany standing out again, where the total lengths of springs, that is travel times, have reduced on almost all links (Fig. 4).
This method functions well to point out network links that have extreme values and thus to shift attention toward components of the network that might need improvements more urgently than others. Spring maps are appropriate when the focus is on one small network because displaying more than one network or a large network with many nodes and edges quickly becomes challenging. For large areas such as Germany as a whole, spring maps are inappropriate for analysing spaces between the included nodes, since the diagrammed higher-tier transport modes such as HSR do not allow for disembarking along the edges without a station.
3.2.5 The Shrivelling Model
The shrivelling model, conceptualised by Mathis (1990) and implemented by L’Hostis (1996, 2009), keeps cities fixed at their geographical position, and draws connections between cities with length proportional to travel time, by using the third dimension. The slower road network is attached to the geographical surface, which is then subject to a complex deformation. Recent developments use the cone as the basic shape for describing terrestrial time–space (L’Hostis and Abdou 2021).
The model can be developed further by including more modes and different speeds, represented by different cone heights. This would resolve the current 'in-or-out' logic regarding the choice of entry points to the fast transport systems, which are represented by cones with equal height, even if their locational and service characteristics differ. By design, the height of cones depends on the density of nodes; the really significant visual variable being the slope of cones, determined by the ratio of speed on roads versus the highest available speed.
3.2.5.1 The Shrivelling Model of German Rail Time–Space
We based the implementation of the shrivelling model of Germany as depicted in Fig. 5 on a list of 21 major cities. In 1990, conventional rail is the fastest terrestrial speed considered at 90 kph, contrasting with the lower speed on the road at 80 kph. Following the shrivelling time–space principle, the ratio for conventional rail and road speed defines the slope of the cones in the representation. In the shrivelling model, the maximum available speed of conventional rail generates the straight line of reference. The terrestrial surface, where road transport occurs, is formed by the assemblage of cones generated from the 21 cities, and cut at the borders of the country. The shrivelled map of 1990, almost flat, exhibits very gentle slopes because the difference between the fastest transport mode and the road is low. By contrast, the German terrestrial time space of 2020 shows a very pronounced relief, where HSR at 170 kph deforms the road surface at 80 kph. We draw the slower classical train connections above the surface where cities are located, with lengths of curves proportional to the timescale.
As opposed to the conventional cartographic view from the top of sub-Fig. 6a), the angle of view in sub-Fig. 6b) reveals the shape of the German time–space. The performance of HSR becomes visible with the long connections between Berlin and Hamburg and Hannover. These long and fast lines crossing spaces with no major intermediary cities generate a marked relief expressing the relative peripheralisation of this intermediate space, despite being located in between the most accessible cities of the country. This feature of the shrivelling map is rendered on no other cartographic representation shown in the paper. While the anamorphosis map generates "blobs" in the periphery, the shrivelled map pushes non-metropolitan spaces below the surface. The area north of Berlin belongs to the 'deepest' parts of German time–space, a position that expresses its relatively low accessibility, as it is expressed as a "blob" similarly on sub-Fig. 3b). Despite enjoying a favourable intermediate position in German geography, the region between Berlin and Hannover lacks direct access to the HSR network and experiences the same fate. Sub-Fig. 6c) shows the same time–space from an unconventional west position, to further underscore the three-dimensional nature of the representation, and to reveal the effect of north–south HSR connections.
4 Evaluation
We assess the maps presented in the previous section according to four properties pertaining to the readability of maps by using the approach suggested by L’Hostis and Abdou (2021), which was introduced in the section "Theoretical Background”. The evaluation leads to an overall readability assessment. A summary of the evaluation results can be found in Table 2.
The first property of time–space, “Acceleration”, requires the ability to display different travel times between distinct parts of time–space maps. By juxtaposition of the same technique for different points in time, i.e. years 1990 and 2020, acceleration can be visualised for all techniques. This is what Spiekermann and Wegener (1994) did in an early paper on time–space. It is generally a challenge to visualise different values in time in just one map and we do not focus on techniques trying to solve this problem.
Isochrone maps show by definition how far in space human movements are possible within specific time intervals, thus meeting the first property. It is possible to retrace transport networks (second property) in isochrone maps, although this depends on the scale of the map, where small-scale maps are advantageous in this regard. On large-scale maps, the used network links can get lost. At the same time, large-scale isochrone maps can visualise impressively disparities of transport networks.
The third property, the co-existence of modes, is possible to be displayed, using different colours for each mode. If multiple time thresholds are to be included in the map, this gets trickier as more creative cartographic solutions are needed. The literature on Bertin’s semiology (1983) may be of avail.
The final property, spatial inversion, is impossible to be mapped explicitly. Implicitly, using topographic knowledge, it could be derived. The overall readability of isochrone maps is high, meaning it is easily readable and not error-prone. For detailed routing visualisation tasks, static isochrones might be the wrong choice. Interactive or dynamic isochrones, however, would allow for spatial inversion and routing. Choropleth maps using accessibility indicators allow for acceleration only via juxtaposition of two maps with different points in time. The mapped accessibility indicators show transformed and indirect acceleration, but not directly on specific origin–destination pairs. Transport networks cannot be drawn into the choropleths as part of the accessibility indicators. A transport network per se can be drawn on top of the choropleth maps and therefore be suggestive of underlying values/colours in the choropleth map. Co-existence of modes is nearly impossible to be mapped. Again, the alternative would be to draw separate items on the map that are not directly related to choropleths. As for spatial inversion, since mapped values in choropleths are only the final results of some computations, they do not show how they were derived geographically. Thus, the fourth property cannot be displayed. In general maps not related to time–space, choropleths are very readable as users are often familiar with the mapped areas (administrative boundaries) and only have to look up the meaning of colours of individual areas in the legend. The same is not true for time–space maps. Regional accessibilities as transformers of acceleration can be displayed, but all other properties are barely or not met. Combining the general high readability with the failure to meet time–space properties leads to medium overall readability for choropleth maps.
Anamorphosis maps are frequently used time–space maps as they are intended to convey the intuition that two points in space connected by shorter travel times than other pairs of points should shrink in perceived distance. They are creative, impressive and intellectually stimulating. The first property, acceleration, is well possible to be mapped. This is true because maps with administrative boundaries are the reference benchmark with the base scenario that travel times are equal in all dimensions and therefore remain undistorted. Comparing anamorphosis maps against the benchmark yields time–space acceleration. All other three properties are not met by anamorphosis maps. Anamorphosis maps are discontinuous space representations, where the real order of proximities is lost. Movements and routing in real space therefore cannot be reenacted. A challenging solution for the co-existence of modes would be to lay on top of each other the anamorphosis maps for each mode, by using monotonically decreasing degrees of transparency for each layer nearer to the top. The overall readability is low as three time–space properties are neglected. Also, knowledge of the geographic space is required to understand the anamorphosis map.
Spring maps are a special case of network representations by drawing edges in an unorthodox fashion, therefore, the second property is satisfied. Acceleration is the primary reason for the invention of spring maps. The longer the distance along all jags of the spring between two points, the slower is the connection. By comparing all springs on a map, acceleration becomes evident. However, this may strike some users as counter-intuitive because they expect that with higher levels of amplitude and frequency of a spring, something “positive”, instead of augmented travel times, has to follow. Co-existence of modes could be depicted by using different colours for each mode if the networks of the modes are sufficiently small. Legibility metrics from the generalisation literature (Stoter et al. 2014) could be used for this task. Still, it is challenging as visualisations may become surcharged quickly. Spatial inversion is difficult or impossible on spring maps for two reasons. First, many springs would have to be drawn, which quickly surcharges the map. Second, it would be difficult to find the fastest route with too many network links involved. The overall readability of spring maps is medium. With sufficiently sparse networks, spring maps should not be overwhelming and therefore easier to read than other visualisations. Spring maps are helpful to understand acceleration and the core network structure, which makes them valuable. Nevertheless, their design is simplistic, the frequency and amplitude are prone to be misunderstood and exact values cannot be extracted from springs visually. Two properties are either not or only partially met. Consequently, their readability is not as high as could be suspected.
Shrivelling maps inherently visualise acceleration on three-dimensional surfaces. Higher peaks and lower troughs convey greater discrepancies of time–space in the case study. Flat terrain represents the absence of fast connections disrupting time–space. The higher the peak, the larger this point’s importance in time–space becomes. When fewer peaks surround a high peak, this shows the high peak’s large sphere of influence. Transport networks are drawn in the shape of arcs on top of the map, thus this property is satisfied. Multiple modes of transport are included in shrivelling maps: first, they are drawn as arcs in parallel and second, they also condition each other by determining the slope of the cones. Spatial inversion is comprehensible for shrivelling maps. For any position on the map, it can be determined in what direction an individual will travel to embark on a faster long-distance mode. In this regard, shrivelling maps resemble time–space cubes. The following is a paradox: despite all four properties of time–space being met, the overall readability of shrivelling maps is low due to the high complexity. It takes time to understand all aspects, which renders the maps impractical in many cases. It is difficult to extract exact travel time distances from the maps. However, shrivelling maps serve different purposes than other techniques and stand out by incorporating spatial inversion, which helps to understand the affiliation of hinterlands to central transport hubs.
In summary, the frequently used isochrone maps have the highest readability but are restrained by their origin-specificity. Choropleth maps are usually highly readable but fail to convey the time–space properties and are restricted to visualising more general value distributions of metrics across space. Anamorphosis maps are very creative and impressive in dynamic live presentations, yet they require detailed study and knowledge of the undistorted space to be intelligible. Spring maps are best suited for presenting transport network edge values out of the suggested methods. Finally, the shrivelling model is catered specifically to time–space visualisations by allowing for a depiction of multiple transport modes and making intelligible the spatial inversion on a map. However, it is designed for advanced use cases and therefore difficult to read.
5 Conclusion
From the thematic point of view, the reunion of five different types of cartographic representations applied to a single dataset, Germany from 1990 to 2020, provides both a comprehensive and an unprecedented view of the transformation of German time–space over the period. Dramatic point-to-point improvements between major metropolises, as in the example of Berlin and Hamburg, are expressed by most representations, each with its own unique flavour. The relative time–space disintegration process experienced by several peripheral or more central regions of the country such as Mecklenburg-Vorpommern (north of Berlin) and Saxony-Anhalt (between Berlin and Hannover) is only expressed by the time–space blobs of the anamorphosis image and by the deep valleys of the shrivelled map. This thematic analysis underlines the benefits of applying truly different points of views on the same geographical object.
From a methodological point of view, no visualisation technique is perfect, all have their advantages and disadvantages. Isochrones are the most popular in travel time visualisations, especially in browser-based interactive tools. Accessibility indicators such as closeness centrality on choropleths remain powerful and frequently used, because they are relatively easily understood. Anamorphoses have the appeal of exposing inaccessible places, but they hide important aspects and cannot deal with multiple modes and spatial inversion. Spring maps are most useful for presenting values on edges of transport networks. Shrivelling maps incorporate the third dimension and are thus more flexible, but require vast efforts both to produce and interpret them.
Visualisations result from a tradeoff between readability, their functionality—comparing places, the possibility of routing—, and their ability to convey the major properties of geographical time–space. A comprehensive and comparative assessment of the readability of these cartographic representations, by means of user tests, still remains to be done.
Data Availability
All data is available upon request.
Notes
A practical tool visualising actual technical maximum speeds on rail tracks is: www.openrailwaymap.org.
References
Ahmed N, Miller H (2007) Time–space transformations of geographic space for exploring, analyzing and visualizing transportation systems. J Transp Geogr 15(1):2–17
Avelar S, Hurni L (2006) On the design of schematic transport maps. Cartographica Int J Geograph Inf Geovis 41(3):217–228
Bertin J (1983) Semiology of graphics. University of Wisconsin Press, Madison
Brath R, Banissi E (2019) Bertin’s forgotten typographic variables and new typographic visualization. Cartogr Geogr Inf Sci 46(2):119–139
Buchin K, van Goethem A, Hoffmann M, van Kreveld M, Speckmann B (2014) Travel-time maps: linear cartograms with fixed vertex locations. In: Duckham M, Pebesma E, Stewart K, Frank AU (eds) Geographic information science, Lecture notes in computer science. Springer International Publishing, Cham, pp 18–33
Bunge W (1962) Theoretical geography. (seconde éd. augmentée 1966 ed.). Gleerup, Lund
Cao J, Liu XC, Wang Y, Li Q (2013) Accessibility impacts of China’s high-speed rail network. J Transp Geogr 28:12–21
Castells M (1996) The information age: economy, society, and culture, volume 1: the rise of the Network Society, vol 1. Blackwell, Cambridge
Cheng X, Liu Z, Zhang Q (2021) MSLF: multi-scale legibility function to estimate the legible scale of individual line features. Cartogr Geogr Inf Sci 48(2):151–168
Erath A, Löchl M, Axhausen KW (2009) Graph-theoretical analysis of the Swiss road and railway networks over time. Netw Spat Econ 9(3):379–400
Fairbairn D, Hepburn J (2023) Eye-tracking in map use, map user and map usability research: what are we looking for? Int J Cartogr 9(2):231–254
Ficzere P, Ultmann Z, Török A (2014) Time–space analysis of transport system using different mapping methods. Transport 29(3):278–284
Field K, Demaj D (2012) Reasserting design relevance in cartography: some concepts. Cartogr J 49(1):70–76
Friedmann J (1986) The world city hypothesis. Dev Chang 17:69–83
Geurs K, van Wee B (2004) Accessibility evaluation of land-use and transport strategies: review and research directions. J Transp Geogr 12:127–140
Grahnert M (2020) Datenbank Fernverkehr—Archiv zum Fernverkehr der Deutschen Bahnen seit 1987
Hägerstrand T (1970) What about people in regional science? Pap Region Sci Assoc 24:7–21
Harvey F, Losang E (2019) Bertin’s matrix concepts reconsidered: transformations of semantics and semiotics to support geovisualization use. Cartogr Geogr Inf Sci 46(2):152–162
Hogräfer M, Heitzler M, Schulz HJ (2020) The state of the art in map-like visualization. Comput Graph Forum 39(2):647–674
Janelle DG (1973) Measuring human extensibility in a shrinking world. J Geogr 72(5):8–15
Kansky K (1963) Structure of transportation networks: relationships between network geometry and regional characteristics. University of Chicago, Chicago
Knowles RD (2006) Transport shaping space: differential collapse in time–space. J Transp Geogr 14(6):407–425
Kraak M (2003) The space–time cube revisited from a geovisualization perspective. In: Proc. 21st international cartographic conference, 1988–96
Krassanakis V, Cybulski P (2019) A review on eye movement analysis in map reading process: the status of the last decade. Geodesy Cartogr 68(1):191–209
Krassanakis V, Cybulski P (2021) Eye tracking research in cartography: looking into the future. ISPRS Int J Geo Inf 10(6):411
L’Hostis A (1996) Transports et Aménagement du territoire: Cartographie par images de synthèse d’une métrique réseau. Mappemonde 3:37–43
L’Hostis A (2009) The shrivelled USA: representing time-space in the context of metropolitanization and the development of high-speed transport. J Transp Geogr 17(6):433–439
L’Hostis A (2016) Misunderstanding geographical distances: two errors and an issue in the interpretation of violations of the triangle inequality. Cybergeo Eur J Geogr (793)
L’Hostis A, Abdou F (2021) What is the shape of geographical time–space? A three-dimensional model made of curves and cones. ISPRS Int J Geo Inf 10(5):340
L’Hostis A, Liu L, Leysens T (2017) Using contact potential measurements to analyse future intercity links made possible by the Tours–Bordeaux High-Speed Rail line. Belgeo. Revue belge de géographie (1)
Letaconnoux J (1907) Note comparative sur la distance en temps entre l’intérieur de la Bretagne et la mer, au XVIIIe, XIXe et XXe si`ecle. Annales De Bretagne 23(3):305–321
MacEachren A (2019) (re)Considering Bertin in the age of big data and visual analytics. Cartogr Geogr Inf Sci 46(2):101–118
Mackinlay J (1986) Automating the design of graphical presentations of relational information. ACM Trans Graph (TOG) 5(2):110–141
Mathis P (1990) Espace et graphe, le p-graphe t-modal 1-planaire. In: Table ronde ASRDLF “Distance et analyse spatiale”, Chamonix. ASRDLF, p 10
Morita T (2019) Reflection on the development of the tool kits of Bertin’s methods. Cartogr Geogr Inf Sci 46(2):140–151
Moyano A, Martínez HS, Coronado JM (2018) From network to services: a comparative accessibility analysis of the Spanish High-Speed Rail System. Transp Policy 63:51–60
O’Sullivan D, Morrison A, Shearer J (2000) Using desktop GIS for the investigation of accessibility by public transport: an isochrone approach. Int J Geogr Inf Sci 14(1):85–104
Plassard F, Routhier JL (1987) Sémiologie Graphique et Evaluation. A.R.T.U.R., Lyon
Raposo P, Touya G, Bereuter P (2020) A change of theme: the role of generalization in thematic mapping. ISPRS Int J Geo Inf 9(6):371
Roth RE, Çöltekin A, Delazari L, Filho HF, Griffin A, Hall A, Korpi J, Lokka I, Mendonça A, Ooms K, van Elzakker CP (2017) User studies in cartography: opportunities for empirical research on interactive maps and visualizations. Int J Cartogr 3:61–68
Sassen S (1994) Cities in a world economy. Pine Forge Press, Thousand Oaks
Schiewe J (2022) Studien zur Gebrauchstauglichkeit. In: Ddd V (ed) Kartographie. Springer Spektrum, Berlin, Heidelberg
Schwarze B (2005) Erreichbarkeitsindikatoren in der Nahverkehrsplanung. Institut für Raumplanung - Universität Dortmund, Dortmund, Arbeitspapier
Shimizu E (1992) Time–space mapping based on topological transformation of physical map. In: W.C.T.R. “Sixième Conférence Mondiale Sur La Recherche Dans Les Transports”, Lyon
Song S (1996) Some tests of alternative accessibility measures: a population density approach. Land Econ 72(4):474–482
Spiekermann K, Wegener M (1993) New time–space maps of Europe. In: Premières Rencontres de Théo Quant, Besancon, p 25
Spiekermann K, Wegener M (1994) The shrinking continent: new time–space maps of Europe. Environ Plan B Plan Design 21:653–673
Stigmar H, Harrie L (2011) Evaluation of analytical measures of map legibility. Cartogr J 48(1):41–53
Stoter J, Zhang X, Stigmar H, Harrie L (2014) Evaluation in generalisation. Abstracting geographic information in a data rich world: methodologies and applications of map generalisation. Springer International Publishing, Cham, pp 259–297
Tobler WR (1961) Map transformation of geographic space. Geography. University of Washington, Washington
Tobler WR (1997) Visualizing the impact of transportation on spatial relations. In: Western Regional Science Association Meeting, Hawaii. Western Regional Science Association, p 7
Touya D, Guillaume HC, Sidonie C (2016) Clutter and map legibility in automated cartography: a research agenda. Cartographica Int J Geogr Inf Geovis 51(4):198–207
Wenner F, Moser J (2020) Which regions benefit from rail accessibility? Germany 1990–2030. Technical report, Chair of Urban Development, Technical University of Munich, München
Wenner F, Thierstein A (2020) Which regions benefit from new rail accessibility? Germany in 2030. disP Plan Rev 56(3):59–76
Wenner F, Thierstein A (2021) Rail accessibility in Germany: changing regional disparities between 1990 and 2020. Spat Res Plann 79(2):95–115
Wu HY, Niedermann B, Takahashi S, Roberts MJ, Nöllenburg M (2020) A survey on transit map layout—from design, machine and human perspectives. Comput Graph Forum 39(3):619–646
Acknowledgements
This paper is supported by project no. 437850433 of the German Research Foundation (Deutsche Forschungsgemeinschaft): "Brain Train?—High-Speed Rail Stations as focal points for the knowledge economy". The support is highly appreciated.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moser, J., Wenner, F. & L’Hostis, A. Visualising Transformations of Geographical Time–Space by Transport Systems. The Case of Germany, 1990–2020. KN J. Cartogr. Geogr. Inf. 73, 301–315 (2023). https://doi.org/10.1007/s42489-023-00151-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42489-023-00151-9