Abstract
In this paper, experimental and numerical investigations on cord–elastomer composites are presented. A finite-element model is introduced, which was developed within the framework of an industrial project. The model is able to simulate an elastomer matrix with inserted cords as load bearing elements and to predict the strains and stresses in cord and elastomer sections. The inelastic material behavior of the elastomer matrix and the yarns is described by corresponding material models suitable for large deformation processes. With the help of a specially developed demonstrator bellows, which is similar to an air spring, the simulation results are compared with experiments. For this purpose, the digital image correlation method is used to determine the deformations on the outer surface of the demonstrator bellows and to calculate the strains on and between the cords. The comparison of the results shows that the employed simulation method is very well suited to predict the strains in these cord–elastomer composites.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Cord-rubber composites nowadays are indispensable in many engineering fields and are essential for the efficient development of many components, e.g., driving belts, tires, or air suspension bellows [5]. These components typically consist of an elastomer, which is reinforced with cords to bear loads. The mechanical properties of these composites are characterized by a high tensile stiffness and a comparatively low stiffness against shear and bending. An important component of these composites are the cords, which consist of at least two yarns of the same or different filament materials. Therefore, the yarn materials determine the field of application of the cord–elastomer composites. The combination of an elastomer matrix with inserted reinforcing material results in an extremely complex mechanical behavior. On one hand, the inelastic and non-linear behavior of the rubber material must be taken into account. On the other hand, the directional dependent and also non-linear and inelastic behavior of the cords have to be regarded.
The calculation methods for cord–elastomer composites can be divided into macroscopic and microscopic approaches. In macroscopic approaches, the structural properties of the composite are homogenized, because the resulting properties of the component are of interest. First, analytical methods were based on the rule of mixtures, with which first important results have been achieved [1, 11, 29, 31]. With the development of the rebar technique, a simple procedure for separate modeling of the cords and the elastomer was found. The basic idea of the rebar technique is inspired by the structure of reinforced concrete. Namely, the concrete is reinforced by inserting steel bars or grids. Transferred to FEM, this means that special bar elements are inserted into elements that should be strengthened. These bar elements have their own material properties, usually with a higher compressive and tensile strength than the host element. This technique quickly became a standard tool of commercial FEM programs. Therefore, a number of works have been published about the simulation of entire cord–elastomer composites with the help of this technique [14, 20, 26, 32]. Macroscopic approaches are typically applied to investigate the global deformation and load behavior of cord–rubber composites. If, however, local quantities, like stresses at the interfaces between cord and elastomer, should be calculated, then microscopic models have to be used. In this context, the level of detail, in which the cords are modeled and the type of material model used, plays a significant role. If, instead of considering the cords as isotropic bodies, the structure of multifilament yarns should also be considered, the modeling effort increases. First approaches for this can be found in [17, 25]. With these approaches, it is possible to describe the filament trajectories analytically. However, the cross-sectional shape of the cord can only be varied slightly, which makes an extension to hybrid cords (i.e., cord consisting of yarns of different materials) and the performance of parameter studies difficult. Another approach by Donner [4] describes the geometry of the cord from a combination of Fourier and Taylor series. Their free coefficients are determined by the help of a finite-element simulation of the cord twisting process and allow a more precise description of the cross-sectional area of the twisted cord. For the validation of cord–rubber composite simulations, experimental tests are performed, which include the measurement of global values like forces, displacements, and rotations of a loading device or the outer contour of loaded bellows, see, e.g., [14]. However, local analyses of strains can significantly extend and improve the database for the comparison with numerical results. Since loaded cord–rubber composite components can show strong inhomogeneous stress and strain fields due to the inhomogeneous material distribution and behavior, a high-performance measuring method for the analyses of deformations on the specimen surface is required. The optical non-contact field measuring method 3D digital image correlation (DIC) is suitable for these local strain analyses. The basics and examples of applications are given in [30]. For strain evaluation based on measured coordinate or displacement fields, various methods are known, like, e.g., local calculations on the basis of on the measured coordinates of adjacent points [10]. Furthermore, a global procedure of strain calculation based on smoothing DIC displacement data using the FEM is given in [2, 30]. Another way is strain calculation based on global functions obtained by approximation using, e.g., polynomials [19, 27] or B-splines (approximation method—see [15], strain calculation on the basis of this method—see [22,23,24]).
In this paper a calculation method is presented, which is based on the microscopic modeling of the cord–elastomer composite by Donner [5]. This method is applied on two demonstrator bellows similar to an air spring with different cord angles in each case, since the cord angle largely determines the mechanical properties of the component. On one hand, this allows the material model and the simulation process to be tested for different configurations, and on the other hand, the results of the simulations are compared with experimentally measured values. Two different material models are used in the simulation, which are introduced in “Material Models”. For the calculation of the elastomer matrix, the Model of Rubber Phenomenology (MOPRH) material by Ihlemann [16] is used in a modified version. For the calculation of the yarns of the cords, a constitutive model is used, which is based on the additive decomposition of the yarn deformation rate [8] into the friction between the filaments of the yarn and the actual elastoplastic filament deformation. Both material models are implemented in Abaqus by the help of the user-subroutine UMAT. “Experimental setup and procedure” then deals with a demonstrator bellows and an experimental setup to analyze cord–rubber composites. The obtained database is used for validation of the numerical results. In this contribution, 3D DIC is used for deformation analysis. Furthermore, a special strain evaluation method regarding tangential directions on the specimen surface is used, which is based on B-spline approximation of the 3D coordinates. Measured global loading test values complement the validation database. Fundamental descriptions of the performed experiments with the material presented in this paper can also be found in [22].
Furthermore, the structure of the simulation model and the procedure for the simulation is shown in “Simulation strategy”. Due to the cyclic symmetry of the demonstrator bellows, the simulation model only comprises a small section and is exactly modeled according to the test specimen. An important point is that the geometry of the cords is determined with a twisting simulation, which is then transferred to the simulation model of the demonstrator bellows via subroutines. Finally, in “Comparison of simulation and experiment”, the comparison of experimental and simulation results is given. In addition to the course of the compressive forces of the demonstrator bellows, a special attention is paid to the comparison of the Hencky strains in the cord and in the elastomer. This area between cord and elastomer is particularly important to make statements about the stresses in the composite component, which are in turn the basis for drawing conclusions about its durability.
Material models
Notation and basic tensorial quantities
The constitutive models to simulate the mechanical behavior of the elastomer matrix and the multifilament yarns are formulated in a large strain framework. Thereby, a tensor notation is employed, where the order of a tensor is denoted by its number of underlines. Based on the deformation gradient  , with its coefficients \(F_{ab}\) with respect to a Cartesian basis vector system
, with its coefficients \(F_{ab}\) with respect to a Cartesian basis vector system  , the local volume ratio J, the left Cauchy–Green tensor
, the local volume ratio J, the left Cauchy–Green tensor  , and the velocity gradient
, and the velocity gradient  are given by:
are given by:

Therein,  is the Lagrangian (material) time derivative. Moreover,
is the Lagrangian (material) time derivative. Moreover,  and \((\bullet )^\mathrm{T}\) are the inverse and the transpose of a second-order tensor, respectively. The deformation rate tensor
and \((\bullet )^\mathrm{T}\) are the inverse and the transpose of a second-order tensor, respectively. The deformation rate tensor  and the spin tensor
and the spin tensor  are defined by:
are defined by:

where \((\bullet )^S\) and \((\bullet )^A\) represent the symmetric part and the antisymmetric part of a second-order tensor, respectively. The isochoric part of the left Cauchy–Green tensor is defined via:

The Zaremba–Jaumann rate \(\overset{*}{(\bullet )}\) of this quantity is defined by (see for example [13]):

This can be reformulated by the help of the subsequent steps. First, the Lagrangian time derivative of Eq. (3) is calculated by:

Next, the identities:

and the time derivative of the volume ratio:

with  being the first principal invariant of a second-order tensor, are substituted into Eq. (5), resulting in:
being the first principal invariant of a second-order tensor, are substituted into Eq. (5), resulting in:

Taking into account the relation  , the substitution of Eq. (8) into Eq. (4) then yields:
, the substitution of Eq. (8) into Eq. (4) then yields:

Finally, the deviatoric part of a second-order tensor

is applied to reformulate Eq. (9), what gives the Zaramba–Jaumann rate of the isochoric left Cauchy–Green tensor:

The Frobenius norm of a second-order tensor  is defined by:
is defined by:

with the double contraction  . Moreover, the \(4^{\mathrm {th}}\)-order isotropic tensor
. Moreover, the \(4^{\mathrm {th}}\)-order isotropic tensor  is introduced by:
is introduced by:

Its application in a double contraction with a second-order tensor  yields the symmetric part
yields the symmetric part  as follows:
as follows:

Material model for elastomer matrix
The mechanical behavior of the elastomer matrix is described by MORPH model, which is able to simulate the non-linear and inelastic material behavior of rubber materials at large strains [3]. In particular, the non-linear stress–strain behavior, the Mullins effect, hysteresis, and permanent set can be captured by this model. The Kirchhoff stress tensor  of the MORPH model is composed out of three contributions according to Eq. (15). Therein, the first term represents a neo-Hookean like contribution,
of the MORPH model is composed out of three contributions according to Eq. (15). Therein, the first term represents a neo-Hookean like contribution,  is an additional stress defined by the ordinary differential equation (16), and the last term is a volumetric contribution according to [12] with the bulk modulus \(K_M\):
is an additional stress defined by the ordinary differential equation (16), and the last term is a volumetric contribution according to [12] with the bulk modulus \(K_M\):


The Zaremba–Jaumann rate of the additional stress  is controlled by a limiting stress
is controlled by a limiting stress  defined by:
defined by:

where the factor  is the maximum value of the Frobenius norm of
is the maximum value of the Frobenius norm of  in the time span \({0\le s \le t}\) of a considered deformation process with current time t. The factors \(\alpha \), \(\beta \) and \(\gamma \) appearing in Eqs. (15)–(17) are parameter functions defined by:
in the time span \({0\le s \le t}\) of a considered deformation process with current time t. The factors \(\alpha \), \(\beta \) and \(\gamma \) appearing in Eqs. (15)–(17) are parameter functions defined by:
Therein, the function \(f(x,y) = \big (x^2 + y^2\big )^{-1/2}\) is employed. Moreover, the factors \(p_1 - p_6\) are additional material parameters. Thus, altogether, the MORPH model includes nine material parameters that have to be defined: the bulk modulus \(K_M\) and the parameters \(p_1 - p_8\). Further information on their physical significance can be found in [16, 21]. A representative stress–strain curve of the MORPH model with the identified parameters listed in Table 1 is presented in Fig. 1.
Therein, the \(1{\mathrm {st}}\) Piola–Kirchhoff stress tensor  (more specifically, the stress component \(T_{xx}\)) is plotted over the stretch \(\lambda _x\) for the case of a uniaxial tension test with multiple loads up to different prescribed maximum stretch values. Therein, the typical phenomena, like hysteresis, Mullins effect, and permanent set can be observed.
(more specifically, the stress component \(T_{xx}\)) is plotted over the stretch \(\lambda _x\) for the case of a uniaxial tension test with multiple loads up to different prescribed maximum stretch values. Therein, the typical phenomena, like hysteresis, Mullins effect, and permanent set can be observed.
Material model for multifilament yarns
The multifilament yarns are simulated by an elastoplastic model with two different plastic yield mechanisms. The first plastic yield mechanism results from the elastoplastic material behavior of the filaments. The second source of plastic yielding is due to frictional sliding between different filaments.
The model is formulated in the framework of large strains using the additive decomposition of the deformation rate tensor (see [7, 8]). Thereby, the total deformation rate of the filaments is denoted by  . Its elastic and plastic contributions are described by
. Its elastic and plastic contributions are described by  and
and  , respectively, such that
, respectively, such that  . The deformation rate of the second plastic yield mechanism, i.e., frictional sliding between different filaments, is denoted by
. The deformation rate of the second plastic yield mechanism, i.e., frictional sliding between different filaments, is denoted by  . Together with a term representing the volumetric deformation rateFootnote 1, the following decomposition of the total deformation rate applies:
. Together with a term representing the volumetric deformation rateFootnote 1, the following decomposition of the total deformation rate applies:

Stresses may only result from elastic deformations, represented by the elastic deformation of the filaments  and volumetric deformations. To calculate the corresponding stress contributions based on a free energy function, the corresponding deformations have to be calculated first. If the deformation gradient is given at any point of time, the volume ratio J and the total deformation rate
and volumetric deformations. To calculate the corresponding stress contributions based on a free energy function, the corresponding deformations have to be calculated first. If the deformation gradient is given at any point of time, the volume ratio J and the total deformation rate  can directly be calculated according to Eq. (2). However, elastic deformations
can directly be calculated according to Eq. (2). However, elastic deformations  can only be calculated if the plastic contributions
can only be calculated if the plastic contributions  and
and  are known. Once they are calculated (see below), the elastic left Cauchy–Green tensor
are known. Once they are calculated (see below), the elastic left Cauchy–Green tensor  can be calculated according to Eq. (11) by the ordinary differential equation:
can be calculated according to Eq. (11) by the ordinary differential equation:

with corresponding initial conditions, for example  for an initially undeformed elastic part. Based on the elastic deformation, a free energy function is introduced by:
for an initially undeformed elastic part. Based on the elastic deformation, a free energy function is introduced by:

Here, \(G_\mathrm{el}\) is the shear modulus, n is an exponent enabling a stiffness increase, and K is the bulk modulus. The corresponding Kirchhoff stress tensor results from the evaluation of the Clausius–Duhem inequality (see for example [13]) as follows:

Plastic yielding of the filaments is described by a von Mises yield function \(\varPhi _\mathrm{pl}\) with a yield stress formulated as a polynomial function with parameters \(a_i\):

Therein,  is the maximum value of the Frobenius norm of the elastic Eulerian Hencky tensor
is the maximum value of the Frobenius norm of the elastic Eulerian Hencky tensor  in the time span \(0\le s\le t\). The Eulerian Hencky tensor
in the time span \(0\le s\le t\). The Eulerian Hencky tensor  thereby results from the solution of the ordinary differential equation
thereby results from the solution of the ordinary differential equation  according to Eq. (11) and subsequent calculation of the tensor function
according to Eq. (11) and subsequent calculation of the tensor function  . The definition of plastic yielding is completed by the flow rule:
. The definition of plastic yielding is completed by the flow rule:

with the plastic multiplier  and the Karush–Kuhn–Tucker conditions:
and the Karush–Kuhn–Tucker conditions:

The second plastic yielding mechanism, i.e., frictional sliding between different filaments, is based on the formulation of the orientation of filaments. To this end, a unit-length tangent vector  representing the current orientation of filaments is employed to define the structural tensor:
representing the current orientation of filaments is employed to define the structural tensor:

If a stress  acts on the filaments, then only a portion of it contributes to friction-relevant shear stresses that lead to frictional sliding between filaments. The corresponding friction-relevant stress tensor
acts on the filaments, then only a portion of it contributes to friction-relevant shear stresses that lead to frictional sliding between filaments. The corresponding friction-relevant stress tensor  is calculated by:
is calculated by:

In particular, frictional sliding should neither be initiated by normal stresses in filament direction nor under equibiaxial stress perpendicular to the filament direction. Thus, these two contributions are filtered out of the total stress tensor  by the help of the last two terms in Eq. (27). Moreover, it follows that the hydrostatic part of the friction-relevant stress tensor
by the help of the last two terms in Eq. (27). Moreover, it follows that the hydrostatic part of the friction-relevant stress tensor  vanishes (i.e.,
vanishes (i.e.,  ).
).
Next, a frictional yield condition \(\varPhi _\mathrm{fric}\) is formulated by the help of the norm of the effective stress  and a term representing the limit between static friction and frictional sliding:
and a term representing the limit between static friction and frictional sliding:

The frictional limit is thereby formulated by a constant minimum threshold \(\tau _{y0}\) and a second contribution that depends on the equibiaxial pressure \(p_\bot \) acting on the filaments and a corresponding parameter \(\mu \) that can be interpreted as the classical Coulomb friction coefficient. The equibiaxial pressure is calculated by:

However, only positive values of \(p_\bot \) (i.e., equibiaxial compression on the filaments) should have an impact on the limit between static friction and frictional sliding. In Eq. (28), this is regarded by the help of the Macauley bracket \({<x> = \mathrm {max}(0,x)}\). Finally, the effective stress  is employed to formulate the flow rule for frictional sliding:
is employed to formulate the flow rule for frictional sliding:

Thereby, the deformation rate tensor  changes neither the filament’s length or their volume nor cross-section. The corresponding inelastic multiplier \(\dot{\chi }_\mathrm{fric}\) appearing in Eq. (30) has to be determined in such a way that the Karush–Kuhn–Tucker conditions:
changes neither the filament’s length or their volume nor cross-section. The corresponding inelastic multiplier \(\dot{\chi }_\mathrm{fric}\) appearing in Eq. (30) has to be determined in such a way that the Karush–Kuhn–Tucker conditions:
are satisfied. Altogether, the constitutive model for multifilament yarns includes 12 material parameters, which are summarized in Table 2. The phenomenological behavior is exemplified in Fig. 9 in “Material parameters”. It shows the resulting behavior based on a tensile test on a twisted standard cord.
Experimental setup and procedure
Specimen and specimen preparation
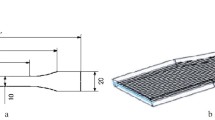
A special demonstrator bellows (sleeve specimen see also in [22]) was designed considering the aim to validate numerical results of load sequences. The fundamental design of the specimen is based on an air spring and consists of an elastomer matrix (special composition) with two embedded cord layers, which are arranged in a cross position. Cord reinforcement of the investigated material presented in this paper is given by polyamide (PA) with cord angles \(\alpha _\mathrm{C}\) of \(10^{\circ }\) and \(35^{\circ }\). To obtain maximum strain differences on the specimen surface, a configuration without elastomer cover layer was used. An illustration of a demonstrator bellows section is given in Fig. 2. The nominal dimensions of the demonstrator are: inner diameter 95 mm, sleeve thickness 1.5 mm, and length 100 mm.
For high-resolution strain analyses on the specimen surface using DIC, fine speckle patterns (stochastic grey scale distributions) are required. These patterns are typically generated by coating. In the present case, the speckles were produced by white paint. High contrast of the coating to the given dark surface (elastomer and cord sections) enabled a speckle production without using a black paint grounding. An example of a demonstrator bellows with coating is given in Fig. 3.
Load case, test setup, and procedure
The tests (see also descriptions in [22]) were performed by means of a servohydraulic test rig, which can be used for tension, compression, and torsion loading, see Fig. 4. Special clamping devices enable fixation of the demonstrator bellows at the top and bottom sides. Furthermore, an internal pressure can be applied to the specimen using the clamping devices.
To analyze different stress states and stress levels, a load sequence was arranged, which includes the following:
-
Adjustment of the initial state with approximately circular cylindrical surface of the specimen and an initial length \(l_0\) (length between the clamping devices, see Fig. 5, nominal value 75 mm)
-
Application of internal pressure (\(p=1 \hbox { bar})\), which is kept constant during the test to prevent the bellows from bulging inward during compression (a higher pressure could loosen the specimen from the clamping device)
-
Loading by axial compression increments of \({{\Delta }s=10 \hbox { mm}}\) (nominal value) with subsequent torsion by \({\beta _T= \pm 1^{\circ }}\) in every compression step
-
Repetition of incremental loading (compression, torsion) until an axial compression of \({s_\mathrm{max}=50 \hbox { mm}}\) (nominal value) is reached.
An example of an unloaded and loaded specimen illustrates already the large amount of deformation occurring in the tests, see Fig. 5.
The deformation analyses on the specimen surface were performed using the 3D DIC system GOM Aramis 4M (4 Megapixel resolution of the two cameras). To this end, image acquisition was carried out in all load steps. To achieve a high-resolution analysis of a surface section, a small measuring volume with horizontal and vertical dimensions of \(25 \hbox { mm}\times 18 \hbox { mm}\) (nominal values) was applied. Additionally, global test rig values (e.g., axial compression, axial force, and torsion angle) were measured and synchronized with the Aramis system via analogue voltage signals. Furthermore, an out-of-plane tracking of the cameras was performed to consider the significant displacements of the analyzed section in out-of-plane direction and the limited depth of field of the used small measuring volume. This out-of-plane tracking and an adaption of the vertical position of the cameras to the middle height position were carried out in the respective loading steps. Since rigid body motions do not influence the strain calculation, these alignments are admissible for strain evaluation.
Evaluation method
The principle of DIC analyses is based on a matching algorithm to identify subsets (called facets in Aramis) representing small surrounding pixel arrays of identification points in the grey scale images, see [30]. To obtain high spatial resolution of the strain analysis, besides the small measuring volume, a small subset (facet) size of 15 pixels (0.18 mm) and a particularly small step size (distance of the identification points) of 4 pixels (0.05 mm, 21 points from cord to cord) were used. Based on the DIC algorithm, the 3D coordinates of the specimen surface in the measuring section are determined as primary results of the DIC analysis.
For the strain determination, a special evaluation method was developed using MATLAB, which is also described in [22]. The reasons for this approach are the increased flexibility and more diverse evaluation possibilities. With this method, various tangential strain measurements (2D) can be calculated from the 3D coordinates in the reference and deformed state determined by DIC. Furthermore, for comparison purposes, the evaluation method can be applied to FE data, as well. The coordinates measured by DIC are approximated using B-spline surfaces (for basic principle, see [15]). Using this procedure, functions for the 3D coordinates are obtained, which enable strain calculation and smoothing of noise given by the measurement data. Based on the tangential directions \({\tilde{u}}\), \({\tilde{v}}\) (for the reference state), and u, v (for the deformed state), the 2D deformation gradient  is calculated. Its coefficients are denoted by:
is calculated. Its coefficients are denoted by:

An illustration in principle of the local \(\tilde{u}\)- and \(\tilde{v}\)-directions on a cylindrical specimen is given in Fig. 6a.
As an appropriate strain measure for large deformations, the Lagrangian Hencky tensor (true strain tensor, based on the deformation gradient) is introduced, given by:

Furthermore, the Green–Lagrange strain tensor is calculated by:

For an arbitrarily rotated \({\tilde{\xi }}\)–\({\tilde{\eta }}\) coordinate system (this could, for example, be oriented in the direction of cord reinforcement), the shear angle \(\theta _{\xi \eta }\) is defined as follows using the coefficients of the Green–Lagrange strain tensor:
The orientation of the evaluation directions \({\tilde{\xi }}\) and \({\tilde{\eta }}\) aligned to the cord angle \(\alpha _\mathrm{C}\) is depicted in principle in Fig. 6b.
Simulation strategy
In this section, a strategy for the simulation of loading scenarios on the demonstration bellows is introduced. Thereby, the FE software Abaqus is used. First of all, the geometry and the properties of the cords have to be determined. To this, an FE simulation of the cord twisting process has to be performed (see “Cord twisting simulation”). Based on the model of the twisted cord, the material parameters of the multifilament yarn model introduced in “Material model for multifilament yarns” are identified. The corresponding identification strategy is presented in “Material parameters”. The model for the simulation of the demonstration bellows and measures to stabilize the simulation model numerically are presented in “Simulation model for the demonstrator bellows”. Finally, two different load sequences on the demonstration bellows are compared in “Load sequence”. The final comparison of simulation results with experimental can be found in “Comparison of simulation and experiment”.
Cord twisting simulation
In the here used microscopic method to simulate cord–elastomer composites, the geometry, the frictional sliding, and the elastoplastic material behavior of the cords are explicitly considered and modeled. To determine the geometry of the twisted cord, a so-called twisting simulation is performed at first. Starting point of this simulation are two or more parallel cylindrical yarns, which are modeled as separate bodies. These yarns consist of an almost infinite number of filaments, whose helical structure is determined by a continuum mechanical material by Donner [5]. The filaments are already twisted with the pre-twist \(v_\mathrm{G}\). In a second step, the yarns of the cord are twisted with a cord twist \(v_\mathrm{C}\) under a constant tensile force in the opposite direction of the pre-twist. Finally, the yarns undergo a thermal shrinkage. This simulation includes all relevant manufacturing steps of the twisting process. The length of the yarns in the twisting simulation is reduced to representative size and the necessary loads are applied to the yarns with non-linear constraints from Jing [18]. The advantage of using these constraints is that surface effects of the yarns are avoided, thus reducing the model size. Nevertheless, a certain number of elements are still necessary to calculate the contact between the yarns. Additional and more complex documentation about the simulation of the twisting process can be found in [5,6,7, 9]. Figure 7 shows the comparison between a simulated cord-cross-section, resulting from the twisting simulation, and a cut surface view from an electron microscope image.
Comparison between a cord-cross-section from an electron microscope (a) [28] and twisting simulation (b)
After completing the twisting simulation, the geometry parameters of the cord are transferred to the simulation model of the demonstrator bellows introduced in Sect. “Simulation model for the demonstrator bellows”. Depending on the position of the FEM integration points, the respective material model, i.e., cord or elastomer, is assigned. Figure 8 shows the resulting material distribution on a cut view of the cross-section of the demonstrator bellows model. Therein, the red and green elements show the distribution of the cord material. It can be seen that the material distribution is different for each cord, as the cords run through the bellows wall in different orientations. Furthermore, the cross ply of the cords is clearly visible.
Material parameters
The material model introduced in “Material model for multifilament yarns” enables the simulation of multifilament yarns. Thereby, the final properties of the yarns are not only determined by the material behavior of the fibres and the frictional properties between the fibres, but also strongly rely on the twisting properties. The adaptation of the free parameters of the material model for multifilament yarns is performed in several steps. For this study, it was carried out for the case of a standard cord with two yarns made of polyamide filaments. First of all, the plastic parameters \(a_1\)...\(a_6\) are adjusted with a simple untwisted cord model on a tensile test. As a second step, the elastic parameters \(G_\mathrm{el}\) and n are adjusted on the same test using a the twisted cord FE model from “Cord twisting simulation”, while the hardening parameters \(a_1\)...\(a_6\) remain fixed. The bulk modulus K is calculated from the initial Poisson ratio \(\nu \) and the shear modulus \(G_\mathrm{el}\):
The parameters of the material model for considering the filament friction \(\tau _{\text {Y}}^0\) and \(\mu \) are set manually. In Table 3, the determined parameters are summarized.
The corresponding material behavior is shown in Fig. 9. Note that the load curve used for this figure does not reflect the load curve used during the parameter adjustment.
Simulation model for the demonstrator bellows
Since the demonstrator bellows has a cyclic symmetry, only 1/296 of the bellows is simulated using cyclic boundary conditions. The width of this section corresponds to the laying length of the cord, which describes the length of the periodic helical structure of the cord. According to the demonstrator bellows presented in “Experimental setup and procedure”, the resulting FE model consists of 4 layers, as shown in Fig. 10. As already mentioned, a cover layer is neglected in comparison to an air spring bellows. This enables the measurement of deformations on the cords and on the elastomer with the DIC method.
However, the simulation model is not suitable for evaluating the local stresses in the elastomer and in the cord, because the selected mesh resolution is too coarse. A suitable method for evaluating the stresses is the use of RVEs (representative volume elements). A detailed explanation of how these RVEs can be used to evaluate stresses in cord–elastomer composites can be found in [9].
Figure 11 shows the boundary conditions which are used. Both top and bottom of the bellows are fixed permanently to the clamp over a defined area of the bellows wall. The upper clamping is movable in vertical direction and is used to apply axial compression loading. Like in the experiment, the inner side of the bellows is additionally loaded with a constant pressure p during the simulation. The clamping of the bellows at the top and bottom is additionally supported by contact conditions between the bellows wall and the clamps to consider the rolling of the bellows over the clamping radius.
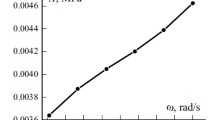
Due to the small bending radii of the cords and the contact near the clamping, some numerical problems were noted. Therefore, the model had to be modified to stabilize the numerical behavior of the simulation. Basically, different mesh resolutions can be used at different regions in the strip model. As already shown in Fig. 10, the cord–elastomer layers are meshed with the double mesh resolution, which improves the accuracy of the evaluation quantities in these layers. However, the doubling of the mesh fineness is only applied to the center of the bellows. An optimization of the mesh has shown that a coarser meshing of the cord–elastomer layers in the near of the clamping can significantly reduce numerical problems, without altering the results of the simulation too much. This stabilization method significantly improves the numerical stability, as can be seen in Fig. 12. A complete convergence of the simulation model can be achieved for both model variants with different cord angles (\(10^{\circ }\) and \(35^{\circ }\)).
Of course, the coarse mesh near the clamps influences the simulation results. However, the effects are small, so that they can be neglected. To demonstrate this, the Eulerian Hencky tensor, based on the left Cauchy–Green tensor  from Eq. (1), is considered, which is given by:
from Eq. (1), is considered, which is given by:

and the strains in circumferential direction \(h_{\varphi \varphi }\) at the surface in the center of the bellows are compared with and without stabilization methods (see Fig. 13). The Hencky strains for the elastomer and the cord are clearly visible in the graph. Since the cord is many times stiffer than the elastomer, the logarithmic strains of the cords are much lower than those of the elastomer. Therefore, maximum values in the diagram belong to the elastomer. Furthermore, it can be seen that the Hencky strains for both model variants do not differ significantly. This holds regardless of the cord angle, which shows that the stabilization methods have almost no influence on the simulation result.
Load sequence
The load sequence used during the simulation differs slightly from these from the experiment according to “Load case, test setup, and procedure”. For the simulation, cyclic torsion between the individual loading steps is not considered. The reasons are, on one hand, that the numerical stability of the simulation model is increased without considering the torsion, and on the other hand, that there are no significant differences for the Hencky strains for cords and elastomer if the torsion is neglected (see Fig. 14). Beside this exception, the load sequence is the same. In the first second of the simulation, the bellows is pressurized with a linearly increasing internal pressure up to \(p = 1 \hbox { bar}\). After the end of this process, the bellows is axially compressed in several stages to approximately \(s_{\text {max}} = 50 \hbox { mm}\) (cf. “Load case, test setup, and procedure”).
Comparison of simulation and experiment
In this section, the experimental results from “Experimental setup and procedure” are compared with the simulation results based on the simulation model described in “Simulation strategy”. For this, the reaction forces at a pilot node and strains are determined in the circumferential direction in the center of the bellows on its outer surface. Due to manufacturing deviations, the cords in the real demonstrator (specimen without cover elastomer layer) protrude slightly from the rubber layer in the initial state (see Fig. 15a). This amplifies the strain differences between cord and elastomer sections, which were analyzed by DIC. Furthermore, the protrusion of the cord sections increases during loading of the demonstrator. In the simulation model, the surface of the bellows is perfect, and therefore, the cords are only visible with very few elements on the outer surface. To achieve comparable results between measurement and simulation, it is necessary to adjust the evaluation depth in the simulation. For this purpose, the evaluation path is shifted inwards by the thickness of an element from the surface (see Fig. 15b). Thus, in the experiment, the strains are determined at the cord surface. In the simulation, approximately, the same position is used.
Force
First of all, force–displacement curves are evaluated. To record the force applied on the demonstrator bellows during the compression process, a pilot node is defined. Since only 1/296 of the bellows circumference is simulated, the force applied on the pilot node is integrated over the entire circumference. In Fig.16, the compressive force for both cord angles can be seen.
Due to the internal pressure, tensile forces act on the clamping at the beginning (i.e., \(s=0 \hbox { mm}\), see Fig. 16). The reason for this is that the clamping is locked, but the bellows wall bulges due to the internal pressure, which leads to initial tensile forces. With the beginning of the axial compression, these tensile forces decrease until a reversal point is reached. From then on, only compressive forces appear. The comparison between simulation and experimental results demonstrates that the force curve of the experiment can be reproduced very accurately.
Strains
The strains were determined using the method described in “Evaluation method”. For adequate comparison, the strains based on simulation data (3D coordinates in undeformed and deformed state) were evaluated using this method, as well. Due to the cyclic symmetry, the evaluation was reduced to a bellows section of \(2\hbox { mm} \times 15\hbox { mm}\) (nominal values, including a 2x1/296 section of the bellows circumference in the FE model for comparison purposes) in the center (regarding axial direction) of the specimen. Strain evaluations presented in this paper are carried out for the maximum compression step (\(s_\mathrm{max}=50 \hbox { mm}\), see “Load case, test setup, and procedure”). Experimental strain field results can also be found in [22].
When comparing experimental and numerical results, the material with cord angle \(10^\circ \) shows qualitatively similar distributions of the Hencky strain \(H_{uu}\) with higher maximum strain values in the simulation, see Fig. 17a. Due to the stiffness differences between the cord and elastomer, large strain differences occur. The deformation is concentrated in the elastomer sections, while the cord sections are almost undeformed. An evaluation along paths in \(\tilde{u}\)- (path 1) and \(\tilde{v}\)-direction (path 2) enables the comparison of the deformation analysis in more detail. The \(\tilde{u}\)-path is defined slightly differing from the middle position of the height, considering an insufficient speckle quality in the middle position. Following path 1, the strain levels of experiment and simulation are nearly the same, see Fig. 17b. Larger maximum FE values occur near the beginning and the end of path 2, see Fig. 17c. Additionally, the cord and elastomer distances in \(\tilde{v}\)-direction show differences between experiment and simulation. An explanation of these deviation can be found in a larger cord angle of \(12.5^{\circ }\) (in contrast to the nominal value of \(10^{\circ }\)) used for evaluation, which was determined experimentally.
The material with cord angle \(35^{\circ }\) shows qualitative similar experimental and numerical \(H_{uu}\)-distributions, see Fig. 18a. The characteristic of large strain differences between cord and elastomer sections, as it already could be observed in the variant with cord angle \(10^{\circ }\) (see, Fig. 17), also occur in the demonstrator bellows with \(35^{\circ }\) cord angle. Higher strain peaks are observed in the experiment, which is confirmed by the path evaluations of \(H_{uu}\) along \(\tilde{u}\)- and \(\tilde{v}\)-directions, see Fig. 18b and Fig. 18c, respectively.
For the analysis of shear deformation, the shear angle \(\theta _{\xi \eta }\) according to Eq. (35) is determined considering evaluation directions aligned to the cord angle \(\alpha _C = 35^{\circ }\) cf. Fig. 6b. In Fig. 19, qualitatively similar distributions with higher magnitudes of the experimental absolute shear angle values compared to simulation are confirmed according to the Hencky strain evaluations.
Generally, for both cord angles, it can be concluded that the experimental and simulation results are in a good agreement.
Conclusion
In this paper, a calculation method is presented, which is based on the microscopic modeling of a cord–elastomer composite. For this purpose, a material model is used for the cords, which takes into account the elastoplastic behavior of the filaments and the frictional sliding between different filaments. The geometry of the twisted cord is described by a combination of Taylor and Fourier series according to [4]. To determine the geometry of the twisted cord, a twisting simulation was carried out. The obtained geometry information was transferred to a demonstrator bellows model, which is similar to an air spring. In contrast to real air springs, the demonstrator bellows is characterized by a simpler geometry and the cover layer was omitted. Loading tests with demonstrator specimens were carried out for validation of the numerical simulations. Thereby, the special demonstrator geometry enabled optical accessibility of a surface with material inhomogeneities. The deformations on the demonstrator surface could be analyzed by means of DIC. Based on the DIC data, strains were analyzed by a special evaluation procedure using Matlab. The occurring large strain differences between cord and elastomer sections on the surface could successfully be determined and provided a suitable database for validation of the simulation results. The comparison of experimental and simulation results shows good agreement, which demonstrates the suitability of the employed simulation strategy, including corresponding material models as well as simulation methods and models.
Notes
The ansatz for the volumetric deformation rate results from the definition of a pure volumetric deformation with the deformation gradient
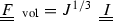 and the calculation of the corresponding deformation rate according to
and the calculation of the corresponding deformation rate according to  .
.
References
Akasaka T, Hirano M (1972) Approximate elastic constants of fiber reinforced rubber sheet and its composite laminate. Compos Mater Struct 1:70–76
Avril S, Feissel P, Pierron F, Villon P (2008) Estimation of the strain field from full-field displacement noisy data. Eur J Comput Mech 17:857–868. https://doi.org/10.3166/remn.17.857-868
Besdo D, Ihlemann J (2003) A phenomenological constitutive model for rubberlike materials and its numerical applications. Int J Plast 19(7):1019–1036. https://doi.org/10.1016/S0749-6419(02)00091-8
Donner H (2011) Anwendungsorientierte modellierung anisotroper struktureigenschaften von Cord-Gummi-Kompositen. Diplomarbeit, Technische Universität Chemnitz
Donner H (2017) FEM-basierte Modellierung stark anisotroper Hybridcord-Elastomer-Verbunde. Ph.D. thesis, Technische Universität Chemnitz
Donner H, Ihlemann J (2013) On the efficient finite element modelling of cord-rubber composites. In: Gil-Negrete N, Alonso A (eds) Constitutive models for rubber VIII. CRC Press, London, pp 149–155
Donner H, Ihlemann J (2014) An anisotropic large strain plasticity model for multifilament yarns. PAMM 14(1):373–374. https://doi.org/10.1002/pamm.201410174
Donner H, Ihlemann J (2016) A numerical framework for rheological models based on the decomposition of the deformation rate tensor. PAMM 16(1):319–320. https://doi.org/10.1002/pamm.201610148
Donner H, Ihlemann J (2017) FE analysis of hybrid cord rubber composites. In: Lion A, Johlitz M (eds) Constitutive models for rubber X. CRC Press, London, pp 437–443
GOM: Aramis tutorial: DIC strain computation basics (2016)
Gough VE (1968) Stiffness of cord and rubber constructions. Rubber Chem Technol 41:988–1021. https://doi.org/10.5254/1.3547240
Hartmann S, Neff P (2003) Polyconvexity of generalized polynomial-type hyperelastic strain energy functions for near-incompressibility. Int J Solids Struct 40(11):2767–2791
Haupt P (2002) Continuum mechanics and theory of materials, 2nd edn. Springer, Berlin
Hohmann F (2017) Vergleich von Simulationsansätzen in der FEM von Luftfedern mit Axialbalg hinsichtlich Fadenhaftung und Submodelltechnik. Masterthesis, Hochschule für Angewandte Wissenschaften Hamburg
Hoschek J, Lasser D (2012) Grundlagen der geometrischen Datenverarbeitung. Teubner, Stuttgart
Ihlemann J (2003) Kontinuumsmechanische Nachbildung hochbelasteter technischer Gummiwerkstoffe. VDI-Verlag, Duesseldorf
Jacob HG (2006) Ein Beitrag zur Berechnung von Faserverbunden aus Elastomeren mit Polyamidfaserverstärkungen. Habilitation, Hochschule für Angewandte Wissenschaften Hamburg
Jiang WG, Yao M, Walton JM (1999) A concise finite element model for simple straight wire rope strand. Int J Mech Sci 41(2):143–161. https://doi.org/10.1016/S0020-7403(98)00039-3
Kirbach C, Lehmann T, Stockmann M, Ihlemann J (2015) Digital image correlation used for experimental investigations of Al/Mg compounds. Strain 51:223–234. https://doi.org/10.1111/str.12135
Kondé AK, Rosu I, Lebon F, Brardo O, Devésa B (2013) On the modeling of aircraft tire. Aerosp Sci Technol 27(1):67–75. https://doi.org/10.1016/j.ast.2012.06.008
Landgraf R, Ihlemann J (2017) Application and extension of the MORPH model to represent curing phenomena in a PU based adhesive. In: Lion A, Johlitz M (eds) Constitutive models for rubber X. CRC Press, London, pp 137–143
Lehmann T, Ihlemann J (2020) Strain analysis of cord-rubber composites using DIC. Mater Today Proc. https://doi.org/10.1016/j.matpr.2020.04.537
Lehmann T, Müller J, Ihlemann J (2018) DIC deformation analyses of Mg specimens at elevated temperatures. Mater Today Proc 5(13):26778–26783. https://doi.org/10.1016/j.matpr.2018.08.151
Lehmann T, Stockmann M, Ihlemann J (2019) A method for strain analyses of surfaces with curved boundaries based on measured displacement fields. Mater Today Proc 12:200–206. https://doi.org/10.1016/j.matpr.2019.03.114
Massmann C (1995) Simulation des Verhaltens von textilen Festigkeitsträgern in Cord-Gummi-Kompositen. Ph.D. thesis, Universität Hannover
Oman S, Nagode M (2013) On the influence of the cord angle on air-spring fatigue life. Eng Fail Anal 27:61–73. https://doi.org/10.1016/j.engfailanal.2012.09.002
Pierron F, Green B, Wisnom MR (2007) Full-field assessment of the damage process of laminated composite open-hole tensile specimens. part i: Methodology. Compos A 38:2307–2320. https://doi.org/10.1016/j.compositesa.2007.01.010
Polley A (2000) Zur Korrelation von Simulationsrechnungen und Ausfallphänomenen bei Rollbalgluftfedern. Ph.D. thesis, Hannover: Universität
Shield CK, Costello GA (1994) Bending of cord composite plates. J Eng Mech 120(4):876–892. https://doi.org/10.1061/(ASCE)0733-9399(1994)120:4(876)
Sutton MA, Orteu JJ, Schreier HW (2009) Image correlation for shape, motion and deformation measurements. Springer, US, New York. https://doi.org/10.1007/978-0-387-78747-3
Walter JD (1978) Cord-rubber tire composites: theory and applications. Rubber Chem Technol 51(3):524–576. https://doi.org/10.5254/1.3535749
Wang W, Yan S, Zhao S (2013) Experimental verification and finite element modeling of radial truck tire under static loading. J Reinf Plastic Compos 32(7):490–498. https://doi.org/10.1177/0731684412474998
Acknowledgements
The authors gratefully acknowledge the financial support from ContiTech AG, Goodyear S.A., Mehler Engineered Products GmbH, and Vibracoustic AG & Co. KG. A special elastomer composition of Vibracoustic AG & Co. KG was used. The demonstrator tests were carried out at Helmut-Schmidt-Universität/Universität der Bundeswehr Hamburg.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Dr Michael Johlitz, Guest Editor of this Special Issue [New Challenges and Methods in Experimental Investigations and Modelling of Elastomers] confirms that where he was co-author of a research article in this Special Issue, he was not involved in either the peer review or the decision-making process of that particular article.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weiser, S., Lehmann, T., Landgraf, R. et al. Experimental and numerical analysis of cord–elastomer composites. J Rubber Res 24, 211–225 (2021). https://doi.org/10.1007/s42464-021-00091-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42464-021-00091-x






















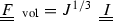 and the calculation of the corresponding deformation rate according to
and the calculation of the corresponding deformation rate according to  .
.