Numerical investigation of mixed convection boundary layer flow for nanofluids under quasilinearization technique

Abstract

The study of boundary layer flow under mixed convection has been investigated numerically for various nanofluids over a semi-infinite flat plate which has been placed vertically upward for both buoyancy-induced assisting and buoyancy-induced opposing flow cases. To facilitate numerical calculations, a suitable transformation has been made for the governing partial differential equations (PDEs). Then, similarity method has been applied locally to approximate the nonlinear PDEs into a coupled nonlinear ordinary differential equations (ODEs). Then, quasilinearization method has been taken for linearizing the nonlinear terms which are present in the governing equations. Thereafter, implicit trapezoidal rule has been taken for integration numerically along with principle of superposition. The effect of physical parameters which are involved in the study are analyzed on the flow and heat transfer characteristics. This study reveals the presence of dual solutions in case of opposing flow. Further, this study shows that with increasing $\phi$ and Pr, the range of existence of dual solutions becomes wider. Also, it has been noted that nanofluids enhance the process of heat transfer for buoyancy assisting flow and it delays the separation point in case of opposing flow.

1 Introduction

Boundary layer flow under mixed convection with heated or cooled surface is a topic of synchronous studies in fluid and thermal sciences. Therefore, to understand the transport phenomena, the study on boundary layer flow is an important concept. There are considerable amount of research works ([1,2,3,4,5, 8] and so on) have been found on the classical theory of boundary layer flow under mixed convection. Merkin [1] studied the boundary layer problem for both buoyancy-induced assisting and opposing flow under mixed convection over a vertical plate. Probably he was the first who gave the idea of flow separation for buoyancy opposing case and Wilks and Bramley [5] first observed the presence of dual solutions for mixed convection buoyancy-induced opposing flow. Then, Merkin [6] also found the dual solutions in a porous medium. Ishak et al. [7] extended the work of Wilks and Bramley for a vertical permeable plate. Thereafter, many investigators (Mahmood and Merkin [8], Ramachandran et al. [9], Ridha [10], Weidman et al. [11], Xu and Liao [12], Ishak et al. [13], Afzal et al. [14]) noticed the presence of dual solutions for different types of boundary layer flow problems.

The common heat transfer fluids are not much effective as expected for the enhancement in heat transfer process for their lower thermal conductivity. With the pioneer invention of ”nanofluid” which is a combination of nano-size particle and a heat transfer fluid, invented by Choi [15] in the year 1995, the study on nanofluids has attracted the attention of researchers for their higher thermal conductivities. In many thermal applications, it has been used potentially. The field of applications of nanofluids are energy storage [16], microbial fuel cell [17], space and defense [18], nuclear reactors cooling [19], heating buildings and reducing pollution [20], industrial cooling [21], nano-drug delivery [22], friction reduction [23], solar absorption [24] and so on.

A review on heat transfer enhancement for nanofluids has been published by Wang and Mujumdar [25], Das et al. [26], and a comprehensive study on heat transfer under convection has been made by Buongiorno [27] in order to analyze the enhancement in heat transfer for nanofluids. It can be inferred that only very few studies have been made for finding dual solutions for nanofluids in case of opposing flow over a flat plate. Bachok et al. [28] were probably the first who observed the presence of dual solutions in their numerical simulation for a vertical plate which was moving in the opposite directions of free stream velocity for a steady-state boundary layer flow problem for nanofluids. However, the effect of $\phi$ was not clearly mentioned on the heat transfer. Rana and Bhargava [29] studied the effect of $\phi$ for various nanofluids on boundary layer flow problem with heated source/sink over a vertical plate which was temperature dependent. They observed that the cooling performance for the vertical plate was highest for the nanofluid having nanoparticle with higher thermal conductivity. However, they did not report about the dual solutions. The boundary layer flow under mixed convection for nanofluid past a thin vertical cylinder was studied by Grosan and Pop [30] by considering the flow as axisymmetric. They observed that the enhancement in heat transfer was also a function of particle concentration and with the changes in small volume fraction of nanoparticles, significant changes had been observed for Nusselt number and skin friction coefficient. Also, they showed that in case of buoyancy opposing flow dual solutions were found. Zaimi et al. [31] showed the presence of dual solutions for the cases of shrinking and stretching in their study of heat transfer past a nonlinear permeable stretching and shrinking sheet. In case of suction, they noticed that the range for dual solutions became wider and temperature reduction was much faster with the increase in particle concentration in nanofluids for a particular range of stretching/shrinking parameter. Patrulescu et al. [32] found the possible range of dual solutions in case of opposing flow when they studied boundary layer flow problem under the mixed convection for nanofluids on a vertical impermeable frustum of a cone. The boundary layer flow under the effects of magneto-hydrodynamic (MHD) through a permeable wedge was studied by Xu et al. [33]. They pointed out that the dual solutions were existed for negative pressure gradient and also observed the small variation in viscosity. Flow separation was delayed in case of suction. In most of the aforementioned works on nanofluids, the researchers have taken Prandlt number (Pr) for small range (0.7-10) in their studies. Due to its highly nonlinearity, the differential equations behave as stiff differential equations for higher Pr. The stiffness can be removed by applying suitable implicit method.

Thus, in the present work, a numerical investigation has been made for boundary layer flow under mixed convection for different nanofluids over a flat plate which has been placed vertically and also both the buoyancy-induced assisting and opposing flow cases are considered in the present work. The main aim of the study is to obtain dual solutions by using an efficient numerical method and then to study the effects of various nanofluids for different parameters on the enhancement of heat transfer. For numerical simulation, an implicit trapezoidal method has been incorporated for numerical integration along with quasilinearization method to overcome the stiffness of higher Pr. Quasilinearization method is a powerful technique to find the dual solutions from a set of nonlinear ODEs and for numerical integration trapezoidal method is a stable method. The detailed discussion on the numerical method has been discussed in the subsequent sections.

1.1 Mathematical formulation

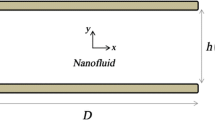
In the present work, we consider an incompressible, two-dimensional, steady-state laminar boundary layer flow under mixed convection for nanofluids over a flat plate which is directed vertically upward as shown in Fig. 1. With the following assumptions on nanofluids, (i) nanofluids are assumed to be Newtonian, (ii) size and shape of the nanoparticles are uniform and well dispersed in the base fluid, (iii) nanoparticles and base fluid are considered to be in thermal equilibrium.

By considering the Boussinesq approximation along with the assumptions, the governing equations for nanofluid can be written as [29]:

$$\begin{aligned}&\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}=0 \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y} =\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^2 u}{\partial y^2}+ \frac{\rho _{s}\beta _{s}+(1-\phi )\rho _{f}\beta _{f} }{\rho _{nf}} g(T-T_{\infty }) \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha _{nf}\frac{\partial ^2 T}{\partial y^2} \end{aligned}$$

(3)

and the boundary conditions along with the

$$\begin{aligned} u(x,0)=0,v(x,0)=0,u(x,\infty )=U_{\infty }, T(x,0)=T_w\,\, \text{ and }\,\, T(x, \infty )=T_{\infty } \end{aligned}$$

(4)

where x and y are along and perpendicular to the semi-infinite vertical flat plate, respectively. u and v are the velocities along x and y directions. $U_\infty$ represents the free stream velocity. Further, viscosity, density, thermal diffusivity, thermal conductivity, and specific heat for nanofluids are given as follows [34]:

$$\begin{aligned} \mu _{nf}= & {} \frac{\mu _{f}}{(1-\phi )^{2.5}}\nonumber \\ \rho _{nf}= & {} (1-\phi )\rho _{f}+\phi \rho _{s}\nonumber \\ \alpha _{nf}= & {} \frac{k_{nf}}{(\rho C_{p})_{nf}}\nonumber \\ \frac{k_{nf}}{k_f}= & {} \frac{(k_s+2k_f)-2\phi (k_f-k_s)}{(k_s+2k_f)+\phi (k_f-k_s)}\nonumber \\ (\rho C_{p})_{nf}= & {} (1-\phi )(\rho C_{p})_{f}+\phi (\rho C_{p})_{s} \end{aligned}$$

(5)

In order to facilitate the numerical computations, equations (1)-(3) have been transformed into another co-ordinate system ($\xi$, $\eta$) by using the relation as follows:

$$\begin{aligned} \eta =y \sqrt{\frac{U_{\infty }}{\nu _{f} x}} , \,\,\, \xi =\frac{x}{L} \end{aligned}$$

along with the stream function and the non-dimensional temperature profile as given by

$$\begin{aligned} \psi =\sqrt{U_{\infty } \nu _{f}x}f(\xi ,\eta ) \end{aligned}$$

and

$$\begin{aligned} \theta (\xi ,\eta )=\frac{T-T_{\infty }}{T_{w}-T_\infty } \end{aligned}$$

where the stream function $\psi$ is related to the variable u and v as $u=\frac{\partial \psi }{\partial y}$ and $v=-\frac{\partial \psi }{\partial x}$. Equations (1)–(3) with the above transformation reduce to

$$\frac{1}{{1 - \phi + \phi \frac{{\rho_{s}}}{{\rho_{f}}}}}\left[ {\frac{1}{{(1 - \phi )^{{2.5}} }}f''' + \left( {(1 - \phi ) + \phi \frac{{(\rho \beta )_{s} }}{{(\rho \beta )_{f} }})} \right)\lambda \theta } \right] + \frac{1}{2}ff'' = \xi \left( {f'\frac{{\partial f'}}{{\partial \xi }} - f''\frac{{\partial f}}{{\partial \xi }}} \right)$$

(6)

$$\begin{aligned}&\frac{1}{(1-\phi )+ \phi \frac{(\rho C_{p})_{s}}{(\rho C_{p})_{f}}}\left[ \frac{1}{Pr}(\frac{k_{nf}}{k_{s}})\theta \;''\right] \nonumber \\&\quad +\frac{1}{2}f\theta \;'=\xi \,\,\,(f\;'\,\,\,\frac{\partial \theta }{\partial \xi }-\theta \;'\,\,\,\frac{\partial f}{\partial \xi }) \end{aligned}$$

(7)

along with

$$\begin{aligned} f(\xi ,0)=0,\,\,\theta (\xi ,0)=1,\,\,f\;'(\xi ,0)=0,\,\,\,f\;'(\xi ,\infty )=1,\,\, \theta (\xi ,\infty )=0. \end{aligned}$$

(8)

as boundary conditions. Here $\lambda$=$R_i \xi$, where $R_{i}=\frac{Gr}{Re^{2}}$, the Richardson number, and $Pr=\frac{\nu _{f}}{\alpha _{f}}$, the Prandtl number, where $Gr=\frac{g\beta _{f}(T_{w}-T_{\infty })L^{3}}{\nu _{f}^{2}}$, the Grashof number and $Re=\frac{U_{\infty }L}{\nu _{f}}$, the Reynolds number.

To solve the nonlinear coupled PDEs (6) and (7), similarity method has been used locally. In this method, the variations with respect to the variable $\xi$ are very small. Thus, equations (6) and (7) become

$$\begin{aligned}&\frac{1}{1-\phi +\phi \frac{\rho _{s}}{\rho _{f}}}\left[ \frac{1}{(1-\phi )^{2.5}}f\;'''+ \left( (1-\phi )+\phi \frac{(\rho \beta )_{s}}{(\rho \beta )_{f}})\right) \lambda \theta \right] \nonumber \\&\quad +\frac{1}{2}ff\;''= 0 \end{aligned}$$

(9)

$$\begin{aligned}&\frac{1}{(1-\phi )+ \phi \frac{(\rho C_{p})_{s}}{(\rho C_{p})_{f}}}\left[ \frac{1}{Pr}(\frac{k_{nf}}{k_{s}})\theta \;''\right] +\frac{1}{2}f\theta \;'=0 \end{aligned}$$

(10)

The physical quantities, the skin friction coefficient $C_{f}$, and the local Nusselt number $Nu_{x}$ are defined as

$$\begin{aligned} C_{f}=\frac{\tau _w}{\frac{1}{2}\rho _{nf}U_{\infty }^2}\,,\ Nu_{x}=-\frac{q_w x}{k_{f}(T_w-T_{\infty })} \end{aligned}$$

(11)

where the shear stress at the wall, $\tau _{w}=\mu _{nf}(\frac{\partial u}{\partial y})_{y=0}$ and the heat flux from plate surface, $q_w=-k_{nf}(\frac{\partial T}{\partial y})_{y=0}$. Thus, after simplification, reduced skin friction coefficient ($C_{f_{rd}}$) and reduced local Nusselt number($Nu_{rd}$) for nanofluids can be written as

$$\begin{aligned} C_{f}[Re]^{0.5}=2\frac{f\;''(\xi ,0)}{(1-\phi )^{2.5}}\,,\,\,\,\,\,\,\, Nu_{x}[Re]^{-0.5}=-\frac{k_{nf}}{k_{f}}\theta \;'(\xi ,0) \end{aligned}$$

(12)

Table 1 Properties for water and nanoparticles [34, 39]

Table 2 Results validation with the previous studies for $(-\theta \;'(0,0))$ with $\lambda =0$ and $\phi =0$ for different Pr

Fig. 1

Buoyancy-induced a assisting and b opposing flow

Fig. 2

Velocity profile for different $\eta _\infty$

Fig. 3

Temperature profile for different $\eta _\infty$

Fig. 4

Profiles for $f\;''(\xi ,0)$ for $\phi =0,0.02,0.05,0.08$ and 0.1 with fixed $Pr=6.7$ for $\lambda < 0$

Fig. 5

Profiles for $-\theta '(\xi ,0)$ for $\phi =0,0.02,0.05,0.08$ and 0.1 with fixed $Pr=6.7$ for $\lambda < 0$

Fig. 6

Profiles for $f\;''(\xi ,0)$ for $Pr=0.1,1,10$ and 100 for buoyancy opposing flow ($\lambda < 0$) for fixed $\phi =0.05$

Fig. 7

Profiles for $\theta '(\xi ,0)$ for $Pr=0.1,1,10$ and 100 for buoyancy opposing flow ($\lambda < 0$) for fixed $\phi =0.05$

Fig. 8

Profiles for $f\;'(-0.1,\eta )$ for different $\phi =0.05$ for buoyancy opposing flow ($\lambda < 0$) for fixed $Pr=6.7$

Fig. 9

Profiles for $\theta (-0.1,\eta )$ for different $\phi =0.05$ for buoyancy opposing flow ($\lambda < 0$) for fixed $Pr=6.7$

Fig. 10

Profiles for $f\;'(-0.15,\eta )$ for different $\phi =0.05$ for buoyancy opposing flow ($\lambda < 0$) for fixed $Pr=6.7$

Fig. 11

Profiles for $\theta (-0.15,\eta )$ for different $\phi =0.05$ for buoyancy opposing flow ($\lambda < 0$) for fixed $Pr=6.7$

2 Numerical method

We introduce local similarity method for approximating nonlinear PDEs (1)-(3) into a set of nonlinear ODEs. Then, quasilinearization technique (Appendix I) has been introduced to linearized the coupled nonlinear ODEs (9)-(10). In this quasilinearization technique, the nonlinear terms are linearizes around a solution profile satisfying the boundary conditions (8). Then, for the solutions, linearized equations are then integrated numerically by introducing a implicit trapezoidal rule which is numerically stable [35] along with the method of principle of superposition. It has been noted that there are no significant changes on the predicted numerical results for η(>10). Thus, $\eta _{\infty }=10$ has been taken for computational purpose. Also, we have found dual solutions for different nominal profiles.

Table 3 For different Pr the values of $f\;''(\xi ,0)$ with $\lambda$=1

Table 4 For different Pr the values of $-\theta \,'(\xi ,0)$ with $\lambda$=1

Fig. 12

Velocity profile with different $\phi$ and $\xi$= 0.2, 0.5, 1 for $Al_{2}O_{3}$-water nanofluid

Fig. 13

Temperature profile with different $\phi$ and $\xi$= 0.2, 0.5, 1 for $Al_{2}O_{3}$-water nanofluid

3 Results and discussion

In the study of boundary layer flow under mixed convection, a numerical study has been made to investigate the behavior of flow variables for buoyancy-induced assisting and buoyancy-induced opposing flow cases for a semi-infinite flat vertically upward plate for different nanofluids. Seven different water-based nanofluids with nanoparticles such as alumina ($Al_{2}O_{3}$), silver (Ag), silica ($SiO_{2}$), copper (Cu), titanate ($TiO_{2}$), zinc oxide (ZnO), and copper oxide (CuO) are taken to analyze the behavior of different nanofluids. The properties of water and solid nanoparticles are illustrated in Table 1. The predicted values $f\;''$($\xi$,0) and -$\theta \;'$($\xi$,0) are plotted for different $\eta _\infty$ in Figs 2 and  3. The step size $\Delta \eta$=0.1 has been taken for numerical computations as it gives the grid independent solutions for $\eta _\infty =10$. The effect of physical parameters involved in the problem such as $\lambda$, $\phi$, $R_i$, Pr, and $\xi$ has been analyzed in the study. After the simulation, the predicted numerical results are displayed in tabular and graphical forms. Table 2 gives the code validation results for $\lambda$= 0 (forced convection) and it is compared with the existing results. It is observed that there is excellent agreement of our present study with previous existing results. Further, we have validated our code with the results of stagnation flow problem with constant temperature over a vertical surface by adding the terms $(1-f'^2)$ and -$f\theta '$ in the governing equations (9) and (10), respectively, for $\phi =0$. The results for $f''(\xi$,0) and $\theta '$($\xi$,0) are validated with previous work of Lok et al. [36], Ramachandran et al. [9], Hassanien and Gorla [37], Ishak et al. [13] as shown in Tables 3 and 4. It seems to be a good agreement with those previous results. Therefore, our developed in-house code can confidently used for numerical computations for our studies.

Figures 4, 5, 6 and 7 display the variation in $C_{f_{rd}}$ and $Nu_{rd}$ with the variation in $\lambda$ for different $\phi$ and Pr. These figures showed the existence of dual solutions, and the dual solutions exist for $\lambda _{cr}<\lambda <0$ only for opposing flows ($\lambda < 0$) for the parameters $\phi$ and Pr, where $\lambda _{cr}$ being the critical values of $\lambda$ and beyond $\lambda _{cr}$, the dual solutions do not exist, whereas, for buoyancy-induced assisting flow ($\lambda \ge 0$), the present numerical method also gives unique solution.

Further, the values of $\lambda _{cr}$ decrease with increasing $\phi$ and such computed values of $\lambda _{cr}$ are $-0.315,\,-0.331$, $\,-0.357$,$\,-0.382,\,-0.402$ for different $\phi =$ $0.0,\, 0.02$, $0.05,\, 0.08, \, 0.1$, respectively (Fig. 4), and for different $Pr=$ $0.1,\,1.0$, $10,\,100$ such values are $-0.143,\, -0.211$, $\, -0.413,\, -0.858$, respectively (Fig. 6). Thus, the predicted range of $\lambda _{cr}$ gradually increases with increasing $\phi$ and Pr. Also, it is observed that the upper solutions (solid lines) are stable and give realistic predictions, whereas the lower solutions (dotted lines) are very much sensitive with initial nominal solution profiles. Further, the nature of dual solutions for both velocity and thermal profiles are plotted for different $\phi$ in Figs. 8, 9, 10 and 11. It has been observed that for upper solution, velocity profiles are increased, whereas they are decreased for the lower solution with increasing $\phi$ and the temperature profiles are increased for both the solutions with the increase in $\phi$.

The effects of $\phi$, Pr, $R_i$ and $\xi$ on the dimensionless velocity profile $f\;'(\xi ,\eta )$ and temperature profile $\theta (\xi ,\eta )$ are plotted in Figs. 12, 13, 14, 15, 16 and 17 for the Ag-water nanofluid for buoyancy assisting flow ($\lambda > 0$). Figure 12 displays the velocity profiles $f\;'(\xi ,\eta )$ for different $\phi$ and $\xi$. It is observed that with the increase in $\phi$, $f\;'(\xi ,\eta )$ decreases and it increases with increasing $\xi$, whereas $\theta (\xi ,\eta )$ is increased for increasing $\phi$ and it decreases when $\xi$ increases (Fig. 13).

In the mixed convection phenomena, the significant effect of buoyancy is characterized by the parameter $\lambda$ where $\lambda =R_i \xi$. $R_i$, the Richardson number, a non-dimensional parameter is defined in terms of the ratio between two non-dimensional parameters, i.e., Grashof number (Gr) and Reynolds number (Re), respectively. Therefore, when $R_i$ increases, then there is an decrements in Re, i.e., it causes the less viscous effect which results the dominance in rising fluid. Thus, with the increase in $R_i$, there is a increment in velocity boundary layer and reduction in temperature in the boundary layer. The same phenomena have been observed in the predicted results as shown in Figs 14 and  15.

Figures 16 and  17 are plotted to see the effect of another non-dimensional parameter, Prandtl number, Pr on $f\;'(\xi ,\eta )$ and $\theta (\xi ,\eta )$, respectively. The Prandtl number is defined between the ratio of momentum diffusivity and thermal diffusivity. Therefore, with increasing Pr, viscosity will be dominant over the thermal diffusivity. Thus, for higher Pr, both velocity and thermal boundary layer thicknesses decrease. Thus, the local Nusselt number gives a significantly higher values. Thus, Prandtl number plays a significant role for enhancing the process of heat transfer. In our study, the predicted results for higher values of Pr have followed same observations as shown in the velocity and temperature profiles (Figs. 16 and 17).

The velocity and temperature distributions for various nanofluids (with nanoparticle $Al_{2}O_{3}$, Cu, CuO, Ag, ZnO, $TiO_{2}$ and $SiO_{2}$ and base fluid as water has been considered) are plotted in Figs. 18 and  19 for fixed $\xi =0.5$ and $\phi =0.05$. It has been observed that velocity and temperature distribution are faster for Ag-water nanofluid, whereas it is lower for $SiO_{2}$-water nanofluid. The order of increasing in velocities has been maintained with the increasing order in thermal conductivities of solid nanoparticles. The temperature reduction for Ag-water nanofluid is faster and lower for $SiO_{2}$-water nanofluid (Fig. 19). Figures 20 and 21 illustrate the variation in $C_{f_{rd}}$ and $Nu_{rd}$ for all nanofluids at $\xi =0.5$ and for fixed $\phi =0.05$. The increment for both the parameters is much faster for Ag-water nanofluid, whereas for $SiO_{2}$-water nanofluid these are lower for both the cases. However, Nusselt number decreases slightly for $SiO_{2}$-water nanofluid with the increase of $\phi$ (Fig. 21).

The variation in the predicted results for $C_{f_{rd}}$ and $Nu_{rd}$ is displayed in Table 5 and 6. In the tables, the behavior of $C_{f_{rd}}$ and $Nu_{rd}$ has shown for the solutions of opposing flow case ($\lambda<$0). It observes that the predicted values of $C_{f_{rd}}$ in case of upper solutions are decreased with the increase in $\xi$, whereas $C_{f_{rd}}$ increases with increasing $\phi$ and Pr. Further, for lower solution, $C_{f_{rd}}$ increases first, and it then decreases with increasing $\xi$. Further, it increases with increasing $\phi$ and decreases for increasing Pr.

In case of $Nu_{rd}$, it increases for upper solutions with increasing $\xi$ and decreases with increasing $\phi$ and Pr . For lower solution, with the increase in $\xi$, $Nu_{rd}$ increases and it decreases for increasing in both $\phi$ and Pr. However, for higher Pr, $Nu_{rd}$ is increased for both the solutions. Further, the effect of different values of $\phi$ and Pr on the $f\;''(\xi ,0)$ has been discussed near separation point (wall shear stress is zero for opposing flow($\lambda <0$)) as given in Tables 7 and 8, respectively. It has also been noted that with the increase in both $\phi$ and Pr, the range of the separation points is also increased. Thus, it can be concluded that separation has been delayed with the increase in $\phi$ and Pr.

Table 5 Results for $C_{f_{rd}}$ and $Nu_{rd}$ for various $\phi$, $\xi$ for buoyancy-induced opposing flow ($\lambda$ 0) for fixed Pr=6.7

Table 6 Results for $C_{f_{rd}}$ and $Nu_{rd}$ for various Pr, $\xi$ for buoyancy-induced opposing flow ($\lambda < 0$) for fixed $\phi$=0.05

Table 7 Effect of $\phi$ and $\xi$ on $f\,''(\xi ,0)$ profile near separation point ($\lambda <0$) for fixed Pr=6.7

Table 8 Effect of Pr and $\xi$ on $f\,''(\xi ,0)$ profile near separation point ($\lambda <0$) for $\phi$=0.05

Fig. 14

Velocity Profile with different $R_i$ with fixed $\xi =0.5$ and $\phi =0.05$ for $Al_{2}O_{3}$-water nanofluids

Fig. 15

Temperature Profile with different $R_i$ with fixed $\xi =0.5$ and $\phi =0.05$ for $Al_{2}O_{3}$-water nanofluids

Fig. 16

Velocity Profile with various Pr with fixed $\xi =0.5$ and $\phi =0.05$ for $Al_{2}O_{3}$-water nanofluids

Fig. 17

Temperature Profile with various Pr with fixed $\xi =0.5$ and $\phi =0.05$ for $Al_{2}O_{3}$-water nanofluids

Fig. 18

Velocity profile for various nanofluids with $\xi =0.5$ and $\phi =0.05$

Fig. 19

Temperature profile for various nanofluids with fixed $\xi =0.5$ and $\phi =0.05$

Fig. 20

Variation on $C{f_{rd}}$ with $\xi =0.5$ and $\phi =0.05$ for various nanofluids

Fig. 21

Variation on $Nu_{rd}$ for various nanofluids with fixed $\xi =0.5$ and $\phi =0.05$

4 Conclusions

Under steady-state condition, a numerical study has been made for boundary layer flow under mixed convection for different nanofluids over a flat plate which has been placed vertically. In this work, both buoyancy-induced assisting and opposing flow cases are considered. To analyze the effect of different physical parameters which are involved in the study, are presented through the figures and tables. The following conclusions are made:

• 1. The existence of dual solutions is found for buoyancy-induced opposing flow case. For increasing $\phi$ and Pr, the existing range of dual solutions is increased. Moreover, this study says that the existing range of solutions gradually increases for increasing Pr as compared to increasing $\phi$.

• 2. $f\;'(\xi ,\eta )$ decreases and $\theta (\xi ,\eta )$ increases with increasing $\phi$ for both the flow cases. Thus, with the inclusion of nanoparticles, enhancement occurs in heat transfer process.

• 3. It has been found that Ag-water nanofluid shows the highest cooling performance where $SiO_{2}$ water nanofluid is the lowest. This observation is followed as the thermal conductivity of Ag is higher, and for $SiO_{2}$, it is lower.

• 4. The $C_{f_{rd}}$ and $Nu_{rd}$ are increased in both the flow cases with the inclusion of nanoparticles. The behavior shows that nanofluids delay the point of separation for opposing flow.

Appendix. quasilinearization method

In quasilinearization technique [38], the nonlinear terms are linearizes around a nominal solution through Taylor’s series expansion by considering only first-order terms. The nominal profile satisfies the boundary conditions (11). After applying the quasilinearization technique to equations (9) and (10) for the $(i+1)$th step in terms of ith step and then simplifying, we obtain the linear ODEs as follows

$$\begin{aligned} { f\;'''_{i+1} +A_if\;''_{i+1}+B_if\;'_{i+1}+C_if_{i+1} +D_if\theta _{i+1}=E_i} \end{aligned}$$

(A.1)

and

$$\begin{aligned} { \theta \;''_{i+1} +P_i\theta \;'_{i+1}+ Q_{i} \, \theta_{i+1}+R_{i} f_{i+1}=F_i} \end{aligned}$$

(A.2)

where ${A_i=-\frac{1}{2}(1-\phi )^{2.5}\,\left( (1-\phi )+\phi \frac{\rho _{s}}{\rho _{f}} \right) \,f_i}$,     $B_i=0$,

$C_i=\frac{1}{2}(1-\phi )^{2.5} \left( (1-\phi )+\phi \frac{\rho _{s}}{\rho _{f}} \right) f\;''_i,$

$D_i=(1-\phi )^{2.5}\, \left( (1-\phi )+\phi \frac{(\rho \beta )_{s}}{(\rho \beta )_{f}})\right) \,\xi \left( \frac{Gr}{Re^2} \right)$,

$E_i=(1-\phi )^{2.5} \left( (1-\phi )+\phi \frac{\rho _{s}}{\rho _{f}} \right) \frac{1}{2}f_if\;''_i$

and

$P_i=-\frac{1}{2} Pr \left( (1-\phi )+\phi \frac{(\rho C_P)_{s}}{(\rho C_P)_{f}} \right) f_i$,     $Q_i=0$,

$R_i=\frac{1}{2} Pr \left( (1-\phi )+\phi \frac{(\rho C_P)_{s}}{(\rho C_P)_{f}} \right) \theta \;'$,

$F_i=\frac{1}{2}Pr \left( (1-\phi )+\phi \frac{(\rho C_P)_{s}}{(\rho C_P)_{f}} \right) f_i\theta \;'_i$

Now, from equations (A.1) and (A.2), a set of first-order ODEs can be obtained by using shooting method and this can be written as

$$\begin{aligned} { \mathbf{y }\;'_{i+1}=\mathbf{A }_i\mathbf{y }_{i+1}+\mathbf{B }_i} \end{aligned}$$

(A.3)

where $\mathbf{A }_i$ is a $5\times 5$ coefficient matrix; $\mathbf{y }= \left[ f,f\;',\;f\;'',\theta ,\theta \;' \right] ^t$ is a solution matrix of order $5\times 1$.