1 Introduction

The ground accelerations applied at the base of structures to carry out dynamic analysis are conventionally assumed to be uniform. However, in large structures -that have an extensive interface with the foundation -this assumption does not coincide with what happens and may give rise to imprecise results. Piping systems, long bridges and dams are examples of such structures.

Many researchers have studied the response of such structures subject to spatially varying ground motions. For this purpose, various numerical methods have been developed, compared and evaluated [1]. For the piping systems, when the variation of input spectra for support points is significant, this approach can be considered as a standard analysis procedure [2].

In the case of long-span bridges, seismic analyses show that the omission of wave passage effects in the conventional response spectrum method brings about incredible results. Since these effects can be included in other methods like random vibration and time history methods, they can predict the structure's response more precisely [3].

For some arch dams, an array of accelerometers has been placed at different locations of the dam to investigate the non-uniform nature of earthquake ground motions at the contact area. Recorded motions of Pacoima Dam show that because of the finite speed, there is a time delay in the earthquake wave propagation from the base to the abutments [4]. Besides, a topographic amplification was recognized at the higher elevations of the abutment relative to the base.

Hall and Alves investigated the time delay and the topographical amplification for 1994 and 2001 earthquakes at Pacoima Dam. The finite element analysis indicated that applying the accelerations recorded at the base of the dam as uniform input leads to a less severe response comparing to the non-uniform input [5, 6]. Chopra and Wang (2010) investigated the seismic responses of Mauvoisin and Pacoima Dams. Results showed that non-uniform excitations could have a notable effect on the dam responses. For the Pacoima Dam, results could recognize the location of actual cracks after the 1994 Northridge Earthquake [7].

Developing of NSAD-DRI program to consider the non-uniform nature of excitations in seismic analysis of arch dams, Sohrabi and Ghaemian investigate the dynamic responses of Karun III and Pacoima Dams [8,9,10]. Comparing computed and recorded displacements of the dams, it was illustrated that in spite of a general agreement between computed and recorded displacements, there were some disconformities. Furthermore, pseudo-static displacement was the predominant part of the response, particularly near the abutment. In this regard, the domination of pseudo-static displacement was more remarkable in vertical and cross-stream directions.

The strong-motion instrumentations of Ertan Dam in Southwestern China recorded some seismic accelerations from 2002 to 2008. In 2017, Jian Yang et al. used five significant recorded motions for system identification of the structure by three various methods. The dynamic response of the dam was computed by linear and nonlinear finite element models considering contraction joints. The comparisons showed that the nonlinear model could lead to more accurate results [11].

In this paper, the dynamic responses of the Karun III dam subjected to the non-uniform seismic accelerations during the earthquake of November 20, 2007, are studied. The EACD-3D-2008 and ABAQUS are used for the finite element analyses. Foremost, recorded displacement during the event is compared with computed ones obtained from the analysis. This comparison is implemented for both uniform and non-uniform input accelerations. In addition, for both assumptions, dynamic tensile stress values during the earthquake are computed by the ABAQUS model. By comparing these data, the effect of non-uniformity on the response of the dam would be evaluated.

2 Karun III dam and ground motions

Karun III Dam is a concrete double arch dam located in the Khuzestan Province, South West of Iran. Its maximum height is 205 m from the foundation and its thickness varies from 29 m at the foundation to 5.5 m at its crest level. The construction phase of the dam finished in 2005. Figure 1 shows a view of Karun III Dam.

Fig. 1
figure 1

View of Karun III dam

Full size image

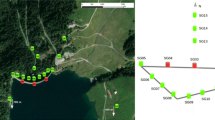
For recording seismic ground motions, an array of 15 accelerometers were placed on several positions of the dam. As can be seen in Fig. 2, seven of them have been placed at the dam foundation interface and the others within the dam body. These accelerometers can record earthquake motions in three directions simultaneously.

Fig. 2
figure 2

Location of accelerometers installed on Karun III dam [9]

Full size image

This array of accelerometers has recorded two earthquakes on November 20 and 21 of 2007. The first one with the PGA of 0.312 g is used in this study. The stream component of this records at various stations is indicated in Fig. 3. The non-uniform nature of ground accelerations along the abutment has already been investigated via these recorded information [12]. This spatial non-uniformity has two aspects, which are called topographic amplification and phase delay. Topographic amplification refers to the higher amplitude of seismic accelerations at higher elevations of the abutment, which is caused by the canyon's topography. Phase delay as the second aspect of the non-uniformity is related to the travel time of incident seismic waves. Since the seismic waves have a limited speed, the travel time along the abutment makes a phase delay between acceleration time-histories at the top and base of the abutment.

Fig. 3
figure 3

Stream component of November 20, 2007 earthquake at S1, S3, S6 and S15 stations

Full size image

In this study, these recorded accelerations are used to define the input ground motions at the dam foundation interface. All of the three components of the earthquake are used after the correction process. These records are filtered through the Butter-Worth approach and the baseline correction is performed by the quadratic method.

3 Governing equations

3.1 The EACD-3D-2008 model

The EACD-3D-2008 is a finite element program for analyzing arch dams which has been developed to take non-uniform input excitations at the dam-foundation interface into account. This program solves the governing equations in the frequency domain and uses the substructure method for numerical modeling. Thus, it includes three substructures: dam, foundation and fluid domain.

For the dam substructure, the equation of motion can be written as:

$$\left[\begin{array}{cc}m& 0\\ 0& {m}_{gg}\end{array}\right]\left\{\genfrac{}{}{0pt}{}{{\ddot{u}}^{t}}{{\ddot{u}}_{g}^{t}}\right\}+\left[\begin{array}{cc}c& {c}_{g}\\ {c}_{g}^{T}& {c}_{gg}\end{array}\right]\left\{\genfrac{}{}{0pt}{}{{\dot{u}}^{t}}{{\dot{u}}_{g}^{t}}\right\}+\left[\begin{array}{cc}k& {k}_{g}\\ {k}_{g}^{T}& {k}_{gg}\end{array}\right]\left\{\genfrac{}{}{0pt}{}{{u}^{t}}{{u}_{g}^{t}}\right\}=\left\{\genfrac{}{}{0pt}{}{{F}_{h}(\omega )}{{F}_{g}(\omega )}\right\}$$
(1)

In this equation, m, c and k are mass, damping and stiffness matrices for unsupported degrees of freedom (DOF). Similarly, mgg, cgg and kgg are the same matrices for supported DOF. In addition, cgand kg are the coupling matrices of damping and stiffness.

The total displacement for unsupported and supported DOF are depicted by \({u}^{t}\) and \({u}_{g}^{t}\), respectively. In the same way, \({\dot{u}}^{t}\), \({\dot{u}}_{g}^{t}\), \({\ddot{u}}^{t}\) and \({\ddot{u}}_{g}^{t}\) indicate velocity and acceleration of unsupported and supported DOF.

Further, Fh and Fg are the hydrodynamic forces from the reservoir and the interaction forces at the dam-foundation rock interface, respectively [7]. The displacements can be divided into pseudo-static and dynamic displacement parts:

$$\left\{\genfrac{}{}{0pt}{}{{u}^{t}}{{u}_{g}^{t}}\right\}=\left\{\genfrac{}{}{0pt}{}{{u}^{s}}{{u}_{g}^{f}}\right\}+\left\{\genfrac{}{}{0pt}{}{u}{{u}_{g}}\right\}$$
(2)

where ufg is defined as free-field displacements by which application pseudo-static displacements (us) are induced. Besides, u can be defined as the dynamic displacement at unsupported DOF which is the result of the remained displacements (ug) at supported DOF. The dependence between \({u}^{s}\) and \({u}_{g}^{f}\) parameters can be indicated as:

$$\left[\begin{array}{cc}k& {k}_{g}\end{array}\right]\left\{\genfrac{}{}{0pt}{}{{u}^{s}}{{u}_{g}^{f}}\right\}=0$$
(3)

Therefore, the pseudo-static displacements can be computed as:

$${u}^{s}=-{k}^{-1}{k}_{g}{u}_{g}^{f}$$
(4)

For the foundation substructure, only dam-foundation interaction is considered and reservoir-foundation interaction is neglected because of its small effects [13]. Boundary elements and a complex-valued impedance matrix (specified in the frequency domain) define the foundation rock area. Equation (5) expresses how the impedance matrix connects interaction forces and relative displacements:

$${S}_{g}\left(\omega \right)\left[{\widehat{u}}_{g}^{t}\left(\omega \right)-{\widehat{u}}_{g}^{f}\left(\omega \right)\right]={\widehat{F}}_{f}\left(\omega \right)=-{\widehat{F}}_{g}\left(\omega \right)$$
(5)

in which Sg(ω) is the impedance matrix and ^ symbol refers to Fourier transform. Ff(ω) is the interaction forces vector at the foundation rock substructure. It is equal and in the opposite direction of Fg(ω), the interaction forces vector at the dam substructure.

In the reservoir substructure, the wave absorption at the lateral and bottom boundaries and the compressibility of water are considered. At the fluid domain the wave equation is the governed:

$$\frac{{\partial }^{2}p}{\partial {t}^{2}} ={c}^{2} {\nabla }^{2}p$$
(6)

in which c and p are the wave velocity in water and the hydrodynamic pressure, respectively. The reservoir substructure includes two parts as the irregular region adjacent to the dam and the regular region in which the shape of the canyon is taken to be similar for an infinite length along with the upstream.

3.2 The ABAQUS model

Governing equations of the model provided by ABAQUS, for the dam and reservoir are the same as EACD-3D-2008 model, considering the equations in ABAQUS are solved in time domain by the implicit method. The foundation rock in ABAQUS, however, is modeled by solid infinite elements [14]. When an unbounded or infinite medium is needed to be defined, using infinite elements is an approach to avoid extending the finite element mesh to a far distance. In this way, by decreasing the number of elements, the time of calculations will be reduced.

Infinite elements define a semi-infinite domain utilizing appropriate decay functions. When these elements are subjected to dynamic loads, plane body waves are considered to travel orthogonally to the boundary. It is assumed that the response of the foundation medium is isotropic and linear elastic. The equilibrium equation can be written as:

$$-\rho \ddot{u}+\frac{\partial }{\partial x} \sigma =0$$
(7)

in which ρ is the density of the foundation material, \(\ddot{u}\) is the material’s particle acceleration, σ is the stress and x is position. For a boundary which is perpendicular to the x axis, plane longitudinal waves can be described as:

$${u}_{x}=f\left(x\pm {c}_{p}t\right)$$
(8)
$${u}_{y}={u}_{z}=0$$
(9)

In Eq. 8, \({c}_{p}\) is the propagation velocity of longitudinal waves and is obtained from the following equation:

$${c}_{p}=\sqrt{\frac{\lambda +2G}{\rho }}$$
(10)

where λ and G are Lamé's constants. In another solution, shear waves can be defined as:

$${u}_{y}=f\left(x\pm {c}_{s}t\right)$$
(11)
$${u}_{x}={u}_{z}=0$$
(12)

or:

$${u}_{z}=f\left(x\pm {c}_{s}t\right)$$
(13)
$${u}_{x}={u}_{y}=0$$
(14)

In these equations, \({c}_{s}\) represent the propagation velocity of shear waves which can be computed by the following equation:

$${c}_{s}=\sqrt{\frac{G}{\rho }}$$
(15)

To prevent longitudinal and shear waves return to the foundation domain, following damping equations are applied at the boundary:

$${\sigma }_{xx}=-{d}_{p}{\dot{u}}_{x}$$
(16)
$${\sigma }_{xy}=-{d}_{s}{\dot{u}}_{y}$$
(17)
$${\sigma }_{xz}=-{d}_{s}{\dot{u}}_{z}$$
(18)

in which dp and ds are damping constants for avoiding the reflection of longitudinal and shear waves. It is shown that for satisfying these equations these constants should be taken as [14]:

$${d}_{p}=\sqrt{\rho (\lambda +2G)}$$
(19)
$${d}_{s}=\sqrt{\rho G}$$
(20)

4 Finite element model

4.1 The EACD-3D-2008 model

The model of meshes for the EACD-3D-2008 program consists of 181 thick-shell elements and 420 nodes for dam body and 805 prismatic elements and 1080 nodes for the reservoir domain. The three dimensional model of the dam body and irregular partition of the reservoir are shown in Fig. 4. Each thick shell element used for the dam substructure has a rectangular form and 8 mid-surface nodes. Mid-surface nodes have five DOFs: x, y and z translations and two rotations of the “normal” which connects the upstream and downstream auxiliary nodes.

Fig. 4
figure 4

The EACD-3D-2008 meshing models of Karun III dam and irregular partition of reservoir

Full size image

The reservoir height is taken to be 180 m, which corresponds to the elevation of the reservoir during the event. According to the experiments, the elastic modulus of the concrete is considered 30 GPa. The Poisson ratio for concrete and foundation rock is considered to be 0.2 and 0.25. Besides, the unit mass of water and concrete is assumed 1000 and 2400 kg/m3, respectively [8].

The computer program's analytical procedure assumes linear behavior for the concrete dam, impounded water and foundation rock. Thus concrete cracking, contraction joints opening during the vibration, or water cavitation are not considered.

In this model, the canyon is assumed to have a uniform cross-section along the stream direction. The impedance matrix (Eq. 5) is obtained by using a direct boundary element method, which reduces the three-dimensional problem at the foundation domain to an infinite series of two-dimensional problems. For this, 38 boundary elements are used at the dam-foundation interface.

4.2 The ABAQUS model.

In the model provided by ABAQUS, physical parameters of the dam, reservoir and foundation are the same as those considered in the EACD-3D-2008 model. In this model dam has 118 continuum solid shell elements and 292 nodes (Fig. 5). Continuum solid shell elements in ABAQUS have only displacement degrees of freedom and use full integration.

Fig. 5
figure 5

The ABAQUS model of meshes for the dam, reservoir and foundation

Full size image

The reservoir is modeled by 480 acoustic elements and 714 nodes. The boundary condition considered for the upstream side of the modeled reservoir (far-end boundary condition) is of the nonreflecting-planar type. At the bottom and sides of the reservoir, boundaries are defined so that the waves are fully absorbed into the materials without reflection.

The model of meshes for the foundation consist of 273 solid elements and 261 infinite elements. As infinite elements are considered, the earthquake waves travel orthogonally to the boundaries. By this, defining the density of the foundation rock does not lead to common inaccuracies which are caused by the return waves. In addition, modeling of the foundation with an enormous number of elements is not necessary.

5 Interpolation of non-uniform excitations

Non-uniform accelerations applied to nodes at the dam-foundation interface has generated by interpolation of recorded accelerations near abutments (S1, S2, S3, S6, S11 and S15). Therefore, recorded accelerations of each accelerometer have assigned to the closest node whereby accelerations of other nodes have been specified by interpolation. For this purpose, to determine Ai (t) which is the acceleration at node i, the following equation has been used based on two recorded accelerations at the stations m and n:

$${A}_{i}\left(t\right)=\frac{{y}_{i}-{y}_{m}}{{y}_{n}-{y}_{m}}\cdot {A}_{n}\left(t+\frac{{y}_{n}-{y}_{i}}{{y}_{n}-{y}_{m}}\cdot {\tau }_{m.n}\right)+\frac{{y}_{n}-{y}_{i}}{{y}_{n}-{y}_{m}}\cdot {A}_{m}\left(t-\frac{{y}_{i}-{y}_{m}}{{y}_{n}-{y}_{m}}\cdot {\tau }_{\mathrm{m}.\mathrm{n}}\right)$$
(21)

where An and Am are acceleration time histories and yn and ym are the corresponding elevations. \({{\varvec{\tau}}}_{{\varvec{m}}.{\varvec{n}}}\) represents propagation time delay of seismic waves between the two accelerometers. This parameter is determined so that the cross-correlation between two acceleration time histories, obtained from the following equation is maximized [5, 13]:

$${C}_{m.n}={\int }_{0}^{T}{A}_{n}\left(t+{\tau }_{m.n}\right){A}_{m}\left(t\right)dt$$
(22)

In this equation T is the duration of the records. Figure 6, shows non-uniform accelerations produced between S2 and S11 accelerometers for the stream, cross-stream and vertical components of the earthquake.

Fig. 6
figure 6

Accelerations produced between S2 and S11 accelerometers for (a) Stream, (b) Cross stream and (c) vertical directions of 20 Nov 2007 earthquake

Full size image

6 Results

6.1 Comparing recorded displacement with computed displacement obtained from EACD analysis.

Applying interpolated accelerations in the EACD-3D-2008 computer program, seismic responses of the dam due to non-uniform excitations are determined. For evaluating the results, computed displacements at the node near to the S12 accelerometer are compared to the recorded displacements. For comparison, computed displacements corresponding to uniform input accelerations are determined and compared, as well. Figure 7 compares the recorded and computed displacements at the crest center (station 12) for the stream, cross-stream and vertical directions.

Fig. 7
figure 7

Recorded and computed displacements at the crest center (S12 station) obtained from the EACD-3D-2008 model in (a) stream, (b) cross stream and (c) vertical directions

Full size image

As can be seen, computed displacements due to non-uniform input accelerations are more coincident in time variation and peak values with recorded displacements. This agreement is outstanding for cross-stream and vertical directions. For better detection, the root mean squared deviation (RMSD) of recorded and computed displacements is presented in the Table 1. According to the table, the non-uniform excitation assumption can reduce RMSD from 13.4 to 28.6 percent.

Table 1 The root-mean-square deviation (RMSD) between recorded and computed displacements at the crest center (S12 station) subjected to uniform ground motions (UGM) and non-uniform ground motions (NGM)
Full size table

Based on Eq. (2), seismic response of the dam due to non-uniform ground motions can be divided into two parts called pseudo-static and dynamic responses. The pseudo-static component indeed is the response of the dam to the static application of spatially varying excitations at abutment nodes. Therefore, the pseudo-static component ratio indicates how much non-uniform excitations affect the response of the dam. Figure 8 shows total and pseudo-static displacements in the stream, cross-stream and vertical directions at crest (station 12). The ratio of the peak values of the pseudo-static component and the total displacement at station 12 is shown in the Table 2.

Fig. 8
figure 8

Total and pseudo-static displacements for non-uniform excitation and in (a) stream, (b) cross stream and (c) vertical directions at crest (station 12)

Full size image
Table 2 The ratio of the pseudo-static to total displacement at station 12 (from EACD-3D-2008 model)
Full size table

6.2 Comparing recorded displacement with computed displacement obtained from ABAQUS analysis

Applying interpolated non-uniform accelerations in the model provided by ABAQUS software is the same as what is explained in the previous section. For evaluating the results, the computed displacements of the crest center for both non-uniform and uniform analyses are compared to the recorded information. Figure 9 shows that, the model subjected to the non-uniform ground motions can reasonably predict the actual displacements. As it can be seen in the Table. 1, in all directions the analysis applying non-uniform ground motions (NGM) can significantly improve the results compared to the analysis which applies uniform ground motions (UGM). This improvement is 15.0, 38.5 and 38.0 percent for the stream, cross stream and vertical directions, respectively. In addition, when non-uniform ground motions are applied, the RMSD between recorded and computed displacements obtained from the analysis of the ABAQUS model, is lower than that of the EACD-3D-2008 model in stream and cross stream directions.

Fig. 9
figure 9

Recorded and computed displacements at the crest center (S12 station) obtained from the ABAQUS model in (a) stream, (b) cross stream and (c) vertical directions

Full size image

6.3 The effect of non-uniformity on tensile stress contours.

The effect of non-uniformity on tensile stress contours can be revealed by the comparison of these contours for the both analyses considering uniform and non-uniform accelerations. Figure 10 depicts peak values of tensile principle stress at upstream and downstream faces for the analysis assuming uniform ground motions. According to the resulted contours, the maximum tensile principle stress at the upstream and downstream faces are 123.5 and 243.2 kPa, respectively. For the analysis considering non-uniform ground motions, the same contours are illustrated in Fig. 11. As it is shown, for this case, the maximum tensile principle stress at the upstream and downstream faces are 529.8 and 539.2 kPa, which is considerably higher than those obtained from the previous analysis. This comparison demonstrates that non-uniformity can dramatically increase tensile principle stress values.

Fig. 10
figure 10

Peak values of tensile principle stress (Pa) at (a) upstream and (b) downstream faces, obtained from the ABAQUS model due to uniform ground motions

Full size image
Fig. 11
figure 11

Peak values of tensile principle stress (Pa) at (a) upstream and (b) downstream faces, obtained from the ABAQUS model due to non-uniform ground motions

Full size image

7 Discussion

According to the results, if the seismic accelerations applied to the dam-foundation interface are spatially uniform, the analysis underestimates the tensile stress values at both upstream and downstream faces. It has been shown that principal tensile stress values due to the interpolated accelerations can be about three times larger than those when ground motion is considered to be uniform. It should be noticed the tensile stress created by both dynamic and static loads can lead to cracking in concrete. Thus, dynamic tensile stress values should be computed as accurate as possible. In spite of values, results demonstrate that if the non-uniformity is neglected, the pattern of stress contours might be affected, so that the location of maximum stress values and accordingly possible cracks cannot be predicted.

Two different programs (ABAQUS and EACD-3D-2008) are used to compute crest center displacements. There are major differences between these programs which are mentioned in Table 1. In the ABAQUS analysis, the equations are solved in the time domain, the dam is modeled by continuum solid shell elements which have only displacement DOFs and the foundation is modeled by a combination of finite and infinite solid elements. In the EACD-3D-2008 analysis, the equations are solved in the frequency domain, the dam is modeled by thick-shell elements which have transitional and rotational DOFs and the foundation is modeled using boundary elements and a complex-valued impedance matrix. As results show, both analysis can appropriately estimate occurred displacements at the crest center. However, displacement time histories obtained from the ABAQUS model in horizontal directions are slightly more consistent than those obtained from the EACD model. Since for simplification of the geometry, spillway openings are neglected, slight differences between recorded and computed displacements seem normal.

The comparison of recorded and computed displacements (obtained from both ABAQUS and EACD models) subjected to uniform and non-uniform input accelerations illustrates that taking non-uniform excitations into account leads to a reduction in the root mean square deviation (RMSD) of recorded and computed displacements at the crest center. Therefore, the estimated displacements of the dam using non-uniform ground motions are more in agreement with the actual recorded responses compared with that of uniform ground motions. Besides, this assumption improves the prediction of peak values of displacements which are an indication of the critical loads that are applied to the dam during the earthquake.

Finally, the pseudo-static component (computed by the EACD analysis) has a considerable proportion of total displacements, especially in cross-stream and vertical directions (where these ratios are 71% and 40%, respectively). This statement demonstrates that the seismic response of the dam is significantly affected by the non-uniformity of earthquake accelerations.

8 Conclusions

In this paper, recorded non-uniform ground motions that shacked Karun III dam on 20 November 2007 are used to study the dam’s response. Dynamic analysis is implemented by two programs (EACD-3D-2008 and ABAQUS) which use different approaches.

It is demonstrated that when non-uniform ground motions are taken into account, both approaches can appropriately estimate time variation and peak values of the recorded displacements near the crest center. On the other hand, neglecting the non-uniformity of input accelerations leads to less accurate computed displacements and a significant increase in RMSD between computed and recorded data.

Based on the total and pseudo-static computed displacements, the pseudo-static component, which is related to the non-uniformity of ground motions, is a remarkable part of total displacements for all directions and it is the dominant part for the cross-stream direction.

By the ABAQUS model, stress values of all elements at every time interval are computed. The maximum tensile stress envelopes for both uniform and non-uniform input ground motions are compared. Results depict that non-uniform ground motions have a major impact on both the pattern and values of the tensile stress contours.