1 Introduction

Earthquakes are one among the most disastrous events known to humanity that has both socioeconomic and environmental impact. A million earthquakes occur in the world every year, accounting for nearly 60% of all disaster-related mortality. The collapse of buildings causes disastrous damage to humans during earthquakes. Due to high-density populations in metropolitan cities, people are constructing multi-story buildings, metro railways, roadways, long bridges, pipelines for their needs. The occurrence of low-intensity events will produce a massive amount of effects in structural, property damages of human lives. The engineers as well have a concern about the methods to reinforce buildings to withstand such earthquakes.

The attenuation zones (AZs) [1, 2] are unique property of the propagation of elastic waves in periodic structures for the last two decades. The noise control and seismic isolation [3,4,5] are some application which is conducted by this feature (AZ). The surface waves propagate near the free surface of a homogenous solid medium. When surface waves propagate in the periodic system, it produces AZs. The theoretical and experimental concept was provided by [6,7,8]. The discussion about the dispersion relation of surface waves propagating in periodic structures has been provided by [9]. They investigated the propagation of surface waves in one- and two-dimensional periodic structures. The numerical simulation of the responses of a finite regular pile-soil system to a surface-wave insert is simulated to show the effectiveness of the attenuation zone. A theoretical and numerical study by Kim and Das [10] proposed a seismic waveguide consisting of shell-type hollow boxes with holes in their sides based on Helmholtz resonators. The so-called meta-cylinders and meta-boxes can be placed side-by-side to convert seismic energy into sound or heat by the resonance of the air in the cavity. A popular way of realizing deep foundations in geotechnical engineering is by driving a series of piles into the ground to a required depth. These piles can now be considered as cylindrical arranged in the soil to behave like a seismic barrier. The surface-wave propagation in two-dimensional steel periodic structures is suggested by Sun and Wu [11] using a finite difference time domain (FDTD) method. A new wavelet-based way has been provided by Yan et al. [12] to detect the dispersion curves of surface waves in two-dimensional periodic structures of fluid–solid and solid–solid systems. Three different types of fabrics, i.e., fluid–solid, solid–solid and air-connected stubbed substrate, respectively, were taken by [13] to analyze the surface-wave propagation in two-dimensional periodic structures. For the first time, Sue et al. [4] discussed the numerical analysis of both surface and guided waves on the problem of seismic waves based on large-scale mechanical metamaterials to check the probability of a passive isolation strategy. Du et al. [14] proposed a two-dimensional elastic metamaterial with periodically square wood-filled steel piles embedded in soil shield for guided surface waves to achieve a seismic guard. It has been investigated numerically by using finite element method. The first time a complete bandgap was observed for Lamb waves in a periodic composite with cylindrical piles. Chen et al. [15] suggest a new design methodology to create seismic metamaterials that can attenuate surface waves below 10 Hz. Pu et al. [16] proposed the work is to explore surface-wave isolation by periodic piles from the perspective of attenuation zones. They described the dispersion relation to calculate the attenuation zones for surface waves by considering a periodic pile and layered soil system by using the finite element method. Pu et al. [17] is considered the problem Single in-filled trench barriers have been widely investigated to mitigate ground vibrations. This type of application with multi rows of in-filled trenches are very restricted. The examined the surface waves attenuation zone by using this single in filled trench barriers. Pu et al. [9] solved the problem of the propagation of surface waves in both one- and two-dimensional periodic structures. The 3D numerical model and the dispersion relation of surface waves have been examined for the two-dimensional periodic pile-soil system by applying the finite element method.

In this work, we propose an elastic metamaterial-based seismic barrier for surface waves propagating in dissipative soil. A main goal in this work is to stop potentially destructive seismic surface waves in their tracks. It attempts to tackle the ground vibration problem for civil engineering structures and ground-borne noise for sensitive installations using the principles of seismic metamaterials. This metamaterial-based pile-soil system with the periodic structure and easy presentation can attenuate the propagation of surface waves within a wide range of frequency. The main advantages of this seismic metamaterial are easy implementation and to obtain the wide bandgaps. We execute a detailed study of the influence of geometrical and mechanical parameters of the feasible soil-wood unit cell on the attenuation potential. Therefore, this study provides a new perspective for surface waves (SWs) isolation by periodic structures in practical engineering. We conclude that this metamaterial pile barrier is appropriate for possible applications of protecting all types of infrastructure from earthquakes damages.

2 Dispersion relation

Without considering the body force, we have taken a homogeneous linear elastic medium. The governing equation can be expressed in the following form.

$$\rho \frac{{\partial^{2} {\mathbf{u}}}}{{\partial \varvec{t}^{2} }} - \varvec{ }\nabla .{\text{c}}\nabla {\mathbf{u}} = 0$$
(1)

where ∇ is the differential operator, ρ is the mass density, u is the displacement vector, the notation t is time parameter, and c is the elastic constant. We can write the displacement field by using Floquet–Bloch theory of solid-state physics for periodic structures

$$\varvec{ }{\mathbf{u}}\left( {{\mathbf{r}},{\mathbf{t}}} \right) = {\text{e}}^{{{\text{i}}\left( {{\mathbf{k}} \cdot {\mathbf{r}} -\upomega{\text{t}}} \right)}} {\mathbf{u}}_{{\mathbf{k}}} \left( {\mathbf{r}} \right)$$
(2)

where r denotes the coordinate vector; k = \(\sqrt {{\mathbf{k}}_{{\mathbf{x}}}^{2} + {\mathbf{k}}_{{\mathbf{y}}}^{2} } \varvec{ }\) is the reduced wave vector; ω is angular frequency; and \({\mathbf{u}}_{{\mathbf{k}}}\)(r) is a periodic function. For periodicity, we express the function \({\mathbf{u}}_{{\mathbf{k}}}\)(r) as follows

$${\mathbf{u}}_{{\mathbf{k}}} \left( {{\mathbf{r}} + {\mathbf{R}}} \right) = {\mathbf{u}}_{{\mathbf{k}}} \left( {\mathbf{r}} \right)$$
(3)

where R is the periodic constant.

By using relation (3) in (2), we obtained the following relation

$${\mathbf{u}}_{{\mathbf{k}}} \left( {{\mathbf{r}} + {\mathbf{R}},{\text{t}}} \right) = {\text{e}}^{{{\text{i}}{\mathbf{k}}.{\mathbf{R}}}} {\mathbf{u}}_{{\mathbf{k}}} \left( {\mathbf{r}} \right)$$
(4)

A unit cell can replace a periodic structure with the periodic boundary condition of Eq. (4). In the case of free boundary conditions, a semi-infinite system deals with surface-wave problems. In [13], the authors have considered a fixed boundary condition at the bottom of the unit cell with large parameter depth (h) as the displacement of surface waves downfalls quickly along with the depth. Here unit cell can be expressed in the form of the eigenvalue equation

$$({\mathbf{\Omega }}({\mathbf{k}}) - \omega ^{2} {\mathbf{M}}) \cdot {\mathbf{u}} = {\mathbf{0}}$$
(5)

where the wave vector is k, and the stiffness and mass matrices are Ω(k) and M. The eigenvalues equation has been obtained by using periodic boundary condition Eq. (4) and fixed boundary condition of the unit cell (i.e., u = 0) into account. The software COMSOL Multiphysics 5.3 has been used to analyze Eq. (5) for all given reduced wave vector k. At the top surface of the unit, the cell is traction free and the bottom surface is adopted by Dirichlet’s boundary condition. So, the stress components will be zero on those surfaces. Here we add a thin layer to the pile structure to difference the surface waves in every surface of the unit cell. The wave vector k of a periodic structure has been scanned in the first Brillouin zone, so we can get the corresponding eigenfrequency x. In this way, the dispersion relation of the periodic structure can be obtained. It is sufficient to scan the wave vector along with the first boundary irreducible Brillouin zone for the reason of uniformity of the first Brillouin zone. We can get both wave modes and other modes for periodic pile-soil systems from Eq. (5). A postprocessing program needs to be implemented to obtain pure surface-wave dispersion relation. The details have been discussed in [18].

3 Model analysis

The eigenvalue problem in Eq. 5 can be solved using a numerical approach based on the finite element method. Specifically, we choose COMSOL Multiphysics [19], a commercially available FEA tool. Boundary conditions with Floquet periodicity can be readily implemented in COMSOL using the Solid Mechanics Module, which is the reason why it has been preferred over other software. The unit-cell geometry is meshed using Lagrange quadratic tetrahedral mesh elements. The linear system of equations in the ‘eigenfrequency’ analysis mode is solved by a direct solver PARDISO, which is also the fastest among the available direct solvers. For each given wave number k, a corresponding eigenfrequency and eigenmodes are obtained.

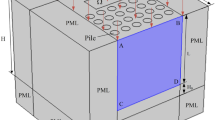
The unit cell has a periodicity ‘a’ in the physical space, and thus, \(2\pi /{\text{a}}\) is periodic in the reciprocal space, i.e., ω (\(k_{x}\)) = ω (\(k_{x}\) + 2π/ax) and similarly ω (ky) = ω (ky + 2π/ay). The unit cell is defined in the extent [− π/ax, π/ax] and [− π/ay, π/ay] in x and y directions, respectively, as shown in Fig. 1. The range consisted of \({\text{k}}_{\text{x}}\) and ky is the well-known first Brillouin zone, as depicted by dashed line in Fig. 2.

Fig. 1
figure 1

Configuration of unit cell a with the square lattice constant a = 4 m, height h = 50 m and cylinder diameter = 2 m, b Rayleigh wave mode shape

Full size image
Fig. 2
figure 2

The first irreducible Brillouin zone for the periodic composites with square lattice: M = (π/ax, π/ay), Γ = (0,0), X = (π/ax,0)

Full size image

For sweeping the k-vector along the boundary Γ-X-M-Γ of the irreducible Brillion zone, a parametric sweep is defined for each subsweep, i.e., ΓX, XM and MΓ separately. Each step in the parametric sweep is solved by an iterative solver. More details for Brillouin zone have been discussed in Ref. [18], and it was proved that the first Brillouin zone can be further reduced as the triangle ΓXM by showing in this work’s Fig. 2 due to the symmetry, which is called as the first irreducible Brillouin zone, so that we can obtain the whole dispersion relations. A set of dispersion curves is then plotted for each wave mode. The dispersion curves are plotted either using MATLAB or Microsoft Excel by exporting the COMSOL output.

4 Parametric study

In this study, we have discussed three major parameters, each parameter produces different results according to their changes of parameters, and such major parameters are: First, variation of geometrical parameters includes four cases, such as unit-cell depth, pile depth, periodic constant and pile diameter. Second, variation of material properties includes wood and soil parameters such as density and shear-wave velocity. We choose soil as a host medium and the standard building materials as the composite materials. In our work, we assume the materials are linear elastic, homogeneous and isotropic. The fixed geometrical parameters and materials properties are taken from following Table 1.

Table 1 Parametric values
Full size table

4.1 Geometrical parameters

The primary goal of this exercise is to maximize the bandgap width while simultaneously minimizing its central frequency, thereby leading to a wide low-frequency bandgap. In all the cases we individually vary one parameter of the unit cell while maintaining all the initial values given in Table 1 for other parameters. First, we study two key parameters corresponding to the unit-cell dimensions: pile spacing and pile height, to see how they affect the bandgap. Placing the pile very close to each other or considerably apart does make a difference as seen in Fig. 3a–c. This is because the bandgaps are driven due to pile rather than the wave scattering due to their periodic arrangement. The pile being away to each other opens a scope for wider bandgaps (periodic constant in Table 2). Thus, space can be optimized when the piles are placed with the highest packing density. We now vary the pile height starting from 15 up to 50 m height. It is to be noted that the total height of the pile is varied, but the thickness is not scaled with the total height. Only the core height is varied as it is not rational to scale the dimensions of the other components. We see that after a height of 15 m there is a sudden drop in the bandgap width (pile depth in Table 2). Thus, a pile height of 15 m is optimal for the desired bandgap.

Fig. 3
figure 3

Dispersion curves of pile inclusion with pile space in a 4 m, b 8 m and c 12 m and pile depth in d 15 m, e 20 m and f 25 m

Full size image
Table 2 The bandgaps for surface waves in different geometrical parameters
Full size table

For cylindrical core of 50 m height and spacing of 2 m the pile diameter is varied, respectively, 2 m, 3 m, 4 m, and the zero frequency bandgaps are becoming wide (Fig. 4 (a), (b), (c)). The unit-cell depth is important as they are providing wide bandgap. We varied the unit-cell depth of 10 m, 30 m and 50 m (Fig. 4d–f) as other all parameters (see in Table 1) fixed. For depth 10 m of the unit cell, first, complete zero frequency bandgap (ZFBG) is found in the frequency range (0–10.5 Hz). Second complete bandgap (CBG) has obtained a frequency range between 94.3 and 123.1 Hz. For depths 30 m and 50 m of the unit cell, only ZFBGs have observed between the frequency ranges 0 Hz and 4.78 Hz and 0 to 2.87 Hz. The bandgap values have shown in following Table 2.

Fig. 4
figure 4

Dispersion curves of pile inclusion with pile diameter in a 2 m, b 3 m and c 4 m and unit-cell depth in d 15 m, e 20 m and f 25 m

Full size image

4.1.1 Influence of geometrical parameters on bandgap

The influence of the unit-cell depth, pile depth, lattice constant and pile diameter was defined to study on the dispersion relationship. The LBF (lower-bound frequency) and UBF (upper-bound frequency) are defined as the lower-bound frequency and upper-bound frequency on the following figure to analyze the surface waves attenuation zone. Figure 5a, b shows the influence of the unit-cell depth and pile depth on the first surface waves attenuation zone. It shows that the lower-bound frequency is fixed and upper-bound frequency decreases gradually and the width of AZ is decreased. The AZs are produced by wave interference and reflection performed at frequencies related to the unit-cell depth and pile depth. So, we can conclude that the bandgap will be wide for low depth of unit cell and low depth pile inclusion into the soil.

Fig. 5
figure 5

Effect of geometrical parameters a unit-cell depth, b pile depth, c lattice constant, d pile side

Full size image

Figure 5c, d shows the effect of periodic constant and pile diameter on the attenuation zone. The lower-bound frequency is fixed for both graphs. The upper-bound frequency of Fig. 5c is increased by increasing the value of periodic constant values. With increasing the value of periodic constant the bandgap width is slightly increasing; after sudden drop, it is increased very high. We can conclude that the more the pile spacing is given, the more the wide bandgap is more effective in the attenuation zone. With increasing the pile diameter, the UBF is linearly increased where LBF is fixed. The goal of this occurrence is that an increase of the pile diameter helps the damaging interference of surface waves.

4.2 Mechanical material parameters

A parametric study is done considering the material properties for the bearing and the host medium which is soil and wood being standard material. After the dimensions of the unit cell are finalized, the material properties can be iterated to find the ones which give us the best band characteristics. The bearing material chosen here has properties similar to [20], which give very wide bandgaps for surface waves. It is observed that when the density of the host material (soil) varies independently within the practical limits, it does not much more influence on the bandgap (Tables 2, 3). The host material in which the waves propagate also plays an important role in deciding the bandgap width and placement. When the shear-wave velocity of the soil is beyond a certain value (Vs > 600 m/s), it positively affects the bandgap as can be seen in Fig. 6b. The high-density wood is suitable to use for the bearing as it performs well. High-density wood is known to provide better durability and thus preferred over the low-density kind which can degrade faster. Besides the density, the shear-wave velocity of wood is also a key parameter to observe the attenuation zone. We took various shear-wave velocity of wood generally varying in the range of 1000–1400 m/s by increasing the scale of 200 m/s, so that we can analyze the result for the range of 1000 m/s, 1200 m/s and 1400 m/s. By using these above values, the CBGs were observed for selecting the shear-wave velocities.

Table 3 The bandgaps for surface waves in different mechanical material parameters
Full size table
Fig. 6
figure 6

Effect of mechanical material parameters a soil density, b soil shear-wave velocity, c wood density, d wood shear-wave velocity

Full size image

These results help in optimizing the geometry and the chosen material properties by permutation over several parameters. Apart from this, in case of discrepancies in the manufacturing (geometry) and variation in material properties, sensitivity analysis helps assess the effect on the dispersion properties of the system. Based on the site on which a structure is constructed, the ground motion which the structures may experience is calculated and would need to be accordingly designed for that demand.

4.2.1 Influence of mechanical material parameters on bandgap

The effect of soil density is shown in Fig. 6a on band structures. The graph of lower-bound frequency is in parallel with the x-axis when the soil density is increased. The upper-bound frequency is decreased. The bandgap width is decreased with increasing soil density. The effectiveness of low soil density on the band structure is high. Figure 6b displays the influence of shear-wave velocity in soil on bandgap. The lower-bound frequency is constant with increasing the shear-wave velocity, but the upper-bound frequency is increased. The bandgap width is becoming wide with high values of soil shear wave. We can conclude that the shear-wave velocity is more effective than soil density on the bandgaps.

Figure 6c, d shows the influence of the wood density and shear-wave velocity. It can be seen that the lower-bound frequency is fixed with increasing the value of wood density and shear-wave velocity in wood, but the upper-bound frequency is increased gradually. So, the bandgap width is increased for both cases. The higher density of wood and shear-wave velocity are more effected on the surface waves attenuation zone.

5 Conclusions

In this work, we have investigated the Rayleigh wave isolation by periodic pile shield from the opinion of periodic Floquet-Bloch theory of solid-state physics. We construct an elastic metamaterial with complete bandgaps (CBG) to separate a region around a protected building from seismic waves. These results show the dispersion analysis, which delivers the information for Rayleigh wave using the infinite number of piles, including band structure. The geometrical and material properties of the architecture play a crucial role in the evolution of CBGs. To conclude the best choice of metamaterial parameters, we report the dependence of BGs on the geometrical parameters of piles and also dependency on material properties of soil and wood. The summarized conclusions and understandings from this study are as follows: The periodic theory of solid-state physics gives a new perception for low-frequency bandgap analysis using an infinite number of piles. When the frequency falls within the attenuation zone, the incident Rayleigh wave decays exponentially along the direction of propagation in pile barriers. The proposed metamaterial concepts and metamaterial structures can be further improved and optimized in the application of interest. Nevertheless, this research tested and demonstrated the feasibility of the suggested new seismic metamaterials strategy, which will be economically considerable in order to achieve a very minimal or no seismic damage to the infrastructure, greatly reducing the socioeconomic loses in the great earthquake events. This work demonstrates not only the promising potential applications as seismic shields but also provides guidelines in the earthquake-resistant design of infrastructures.

6 Data availability

The parametric (soil density, shear-wave velocity, p-wave velocity, wood density, shear-wave velocity, p-wave velocity) values of materials (soil, wood) are taken from Andrea Colombi et al. [20].