1 Introduction

In the recent years, the interest in robotic systems has increased in many application fields [1,2,3,4]. Since these systems are always affected by the environmental disturbances, simple traditional control methods cannot be efficient. Therefore, it is necessary to develop robust controller to suppress the effects of them. To overcome nonlinearities and uncertainties, many robust approaches have been proposed [5,6,7,8,9,10,11,12].

Sliding Mode Control (SMC) is frequently used for controlling systems with uncertainties because of its robustness. Thus, SMC is one of the best choices for robotic systems. The main disadvantage of SMC is the chattering, which may cause damages to the system [13,14,15,16]. In order to decrease the chattering, a dynamic sliding mode control (DSMC) scheme has been presented in [14,15,16]. In this approach, the chattering can be reduced due to the integration method in obtaining the control signal. Meanwhile, Like SMC, the uncertainty bound should be known in the design of DSMC. In this study, to solve this problem, the uncertainty is estimated using various uncertainty estimators such as the Fourier series expansion, Legendre polynomials and adaptive fuzzy systems.

Function approximation methods have been explored to overcome uncertainties in robust control of nonlinear systems [17,18,19,20,21,22,23,24]. In [25], an adaptive dynamic sliding-mode control system (ADSMCS) with recurrent radial basis function network (RRBFN) for indirect field-orientation control induction motor (IM) drive which guarantees the robustness in the presence of parameter uncertainties and load disturbances has been proposed. The ADSMCS includes a dynamic sliding-mode controller (DSMC), an RRBFN uncertainty observer and a robust controller. In [26], a robust adaptive second-order sliding mode control approach has been presented for the tracking control of uncertain linear systems with matched and unmatched disturbances. Excellent mathematical features of fuzzy systems such as universal approximation property and linear parameterization make them very attractive and efficient. According to the universal approximation theorem [27], fuzzy systems can approximate many nonlinear functions with arbitrary accuracy. Recently, some other uncertainty estimators such as Fourier series and Legendre polynomials have been applied to robotic systems [1, 28,29,30,31,32,33]. This paper aims to compare the performances of these estimators.

In this paper, an adaptive DSMC is developed for robust control of robot manipulators. In order to eliminate the need for uncertainty bound, adaptive uncertainty estimators are designed to estimate the lumped uncertainty. Moreover, the robust control term that compensates the reconstruction error is designed so that improves the tracking performance considerably. Simulation studies indicate that increasing the convergence rate plays an important role in reducing the tracking error. In [1, 7, 11, 17, 29, 31, 34], a constant convergence rate is utilized to control robotic systems. However, it may result in initial high control effort if there is an initial tracking error. In order to have a satisfactory control effort at initial times and small steady state tracking error, the convergence rate is increased slowly using a positive exponential function.

The remainder of this paper is organized as follows. Section 2 introduces the dynamic model of the robotic system. Function approximation techniques are summarized in Sect. 3. In Sect. 4, the proposed control law is designed. Section 5 provides the stability analysis. Section 6 illustrates the simulation results. Our conclusions are given in Sect. 7.

2 Modeling

The dynamics of a robotic system driven by DC motors can be presented as [35]

$$D\left( q \right)\ddot{q} + C\left( {q,\dot{q}} \right)\dot{q} + G\left( q \right) = \tau_{l}$$
(1)
$$J_{m} r^{ - 1} \ddot{q} + B_{m} r^{ - 1} \dot{q} + r\tau_{l} = K_{m} I_{a}$$
(2)
$$RI_{a} + L\dot{I}_{a} + K_{b} r^{ - 1} \dot{q} + d = v$$
(3)

The state-space equation of the robotic system can be derived by the use of (1)–(3) as

$$\dot{X} = F\left( X \right) + bv - bd$$
(4)

where

$$X = \left[ {\begin{array}{*{20}c} q \\ {\dot{q}} \\ {I_{a} } \\ \end{array} } \right], b = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {L^{ - 1} } \\ \end{array} } \right], F\left( X \right) = \left[ {\begin{array}{*{20}c} {f_{1} \left( X \right)} \\ {f_{2} \left( X \right)} \\ {f_{3} \left( X \right)} \\ \end{array} } \right]$$
(5)

In which

$$\begin{aligned} & f_{1} \left( X \right) = X_{2} , \\ & f_{2} \left( X \right) = \left( { J_{m} r^{ - 1} + rD} \right)^{ - 1} \left( { - \left( {B_{m} r^{ - 1} + rC} \right)X_{2} - rG + K_{m} X_{3} } \right), \\ & f_{3} \left( X \right) = - L^{ - 1} \left( {K_{b} r^{ - 1} X_{2} + RX_{3} } \right) \\ \end{aligned}$$
(6)

where the vectors \(q \in R^{n }\), \(v \in R^{n}\), \(I_{a} \in R^{n}\) and \(d \in R^{n}\) are the joint positions, motor voltages, motor currents and external disturbances, respectively. The details are completely presented in [29].

Substituting (1) in (2), it follows that

$$I_{a} = K_{m}^{ - 1} \left( {\left( { J_{m} r^{ - 1} + rD} \right)\ddot{q} + \left( {B_{m} r^{ - 1} + rC} \right)\dot{q} + rG} \right)$$
(7)

Now, (3) is rewritten as

$$RI_{a} + K_{b} r^{ - 1} \dot{q} + \varphi \left( t \right) = v$$
(8)

where \(\varphi = L\dot{I}_{a} + d\). Substituting (7) into (8) yields

$$v = RK_{m}^{ - 1} \left( {\left( { J_{m} r^{ - 1} + rD} \right)\ddot{q} + \left( {B_{m} r^{ - 1} + rC} \right)\dot{q} + rG} \right) + K_{b} r^{ - 1} \dot{q} + \varphi$$
(9)

One can easily rewrite (9) as

$$v = \bar{D}\ddot{q} + \bar{C}\dot{q} + \bar{G} + \varphi$$
(10)

In which

$$\begin{aligned} \bar{D} & = RK_{m}^{ - 1} \left( { J_{m} r^{ - 1} + rD} \right) \\ \bar{C} & = RK_{m}^{ - 1} \left( {B_{m} r^{ - 1} + rC} \right) + K_{b} r^{ - 1} \\ \bar{G} & = RK_{m}^{ - 1} rG \\ \end{aligned}$$
(11)

Equation (10) can be rewritten as

$$\begin{aligned} & v = \ddot{q} + f \\ & f = \bar{D}\ddot{q} + \bar{C}\dot{q} + \bar{G} + \varphi - \ddot{q} \\ \end{aligned}$$
(12)

3 Function approximation techniques

In this section, we explain three well-known techniques which can approximate nonlinear functions with arbitrary small approximation error, namely, the Fourier series expansion, Legendre polynomials and adaptive fuzzy systems.

3.1 The Fourier series expansion

Consider a function \(g\left( t \right)\) defined on \(\left[ {t_{1} ,t_{2} } \right]\). According to [1, 29], \(g\left( t \right)\) can be expressed as

$$g\left( t \right) = a_{0} + \mathop \sum \limits_{n = 1}^{\infty } a_{n} \cos \left( {w_{n} t} \right) + b_{n} { \sin }\left( {w_{n} t} \right)$$
(13)

where \(w_{n} = 2n\pi /T\) and \(T = t_{2} - t_{1}\). The approximation error is

$$\varepsilon_{m} \left( t \right) = g\left( t \right) - g_{m} \left( t \right)$$
(14)

where \(g_{m} \left( t \right) = a_{0} + \mathop \sum \nolimits_{n = 1}^{m} a_{n} \cos \left( {w_{n} t} \right) + b_{n} { \sin }\left( {w_{n} t} \right)\) is the approximated value using the Fourier series. It is clear that \(g_{m} \left( t \right)\) can be written as

$$g_{m} \left( t \right) = P^{T} \xi \left( t \right)$$
(15)

where

$$P = \left[ {a_{0} \quad a_{1} \quad b_{1} \quad \ldots \quad a_{m} \quad b_{m} } \right]^{T}$$
$$\begin{aligned} & P = \left[ {a_{0} \quad a_{1} \quad b_{1} \quad \ldots \quad a_{m} \quad b_{m} } \right]^{T} \\ & \xi \left( t \right) = \left[ {1\quad \cos \left( {w_{1} t} \right)\quad { \sin }\left( {w_{1} t} \right)\quad \ldots \quad \cos \left( {w_{m} t} \right)\quad { \sin }\left( {w_{m} t} \right)} \right]^{T} \\ \end{aligned}$$
(16)

3.2 Legendre polynomials

A typical inner product can be expressed as

$$\langle f,g \rangle= \int f^{*} \left( x \right)g\left( x \right)dx$$
(17)

where \(f^{*} \left( x \right)\) is the complex conjugate of the \(f\left( x \right)\). If (17) takes the value of zero, two functions \(f\) and \(g\) are orthogonal. It has been shown in [28, 31] that a function \(h\left( x \right)\) defined on the interval \(\left[ {x_{1} x_{2} } \right]\) can be expressed as

$$h\left( x \right) = \mathop \sum \limits_{i = 1}^{m} a_{i} \xi_{i} \left( x \right) + \varepsilon_{m} \left( x \right)$$
(18)

where the set \(\left\{ {\begin{array}{*{20}c} {\xi_{1} \left( x \right)} & \cdots & {\xi_{m} \left( x \right)} \\ \end{array} } \right\}\) forms an orthogonal basis and \(\varepsilon_{m} \left( x \right)\) is the approximation error or truncation error.

Considering the interval \(\left[ {\begin{array}{*{20}c} { - \,1} & 1 \\ \end{array} } \right]\) and the inner product (17), the Legendre polynomials can be written as

$$\xi_{0} \left( x \right) = 1, \xi_{1} \left( x \right) = x, \left( {i + 1} \right)\xi_{i + 1} \left( x \right) = \left( {2i + 1} \right)x\xi_{i} \left( x \right) - i\xi_{i - 1} \left( x \right)\quad i = 1, \ldots ,m - 1$$
(19)

These polynomials form an orthogonal basis [28, 31, 36]. As a result, a function \(h\left( x \right)\) defined on the interval \(\left[ { - \,1 \quad 1} \right]\) can be approximated using Legendre polynomials in the form of

$$h_{LP} \left( x \right) = \mathop \sum \limits_{i = 1}^{m} a_{i} \xi_{i} \left( x \right) = P^{T} \xi$$
(20)

where

$$\begin{aligned} P & = \left[ {a_{0} \quad a_{1} \quad \ldots \quad a_{m} } \right]^{T} \\ \xi & = \left[ {\xi_{0} \quad \xi_{1} \quad \ldots \quad \xi_{m} } \right]^{T} \\ \end{aligned}$$
(21)

3.3 Adaptive fuzzy systems

Generally, the fuzzy rule has the following IF–THEN form,

$$R^{l} {:}\;IF\; x_{1} \;is\;A_{1}^{l} \; and \ldots x_{n} is A_{n}^{l} , THEN\;y\;is\;B^{l}$$
(22)

where \(x = \left[ {x_{1} , x_{2} , \ldots , x_{n} } \right]^{T}\) and y are the inputs and output of the fuzzy system, respectively; \(l = 1,2, \ldots ,M\) is the number of fuzzy rules, M is the total number of rules; \(A_{i}^{l}\) and \(B^{l}\) are the fuzzy sets described by fuzzy membership functions \(\mu_{{A_{i}^{l} }} \left( {x_{i} } \right)\) and \(\mu_{{B^{l} }} \left( y \right)\) respectively.

When the inputs \(x = \left[ {x_{1} , x_{2} , \ldots , x_{n} } \right]^{T}\) are given, the output y of the fuzzy inference system with singleton fuzzifier, product inference engine and center average defuzzifier can be expressed as [17, 37]

$$y\left( x \right) = \frac{{\mathop \sum \nolimits_{l = 1}^{M} \bar{y}^{l} \left( {\mathop \prod \nolimits_{i = 1}^{n} \mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} \right)}}{{\mathop \sum \nolimits_{l = 1}^{M} \left( {\mathop \prod \nolimits_{i = 1}^{n} \mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} \right)}} = P^{T} \xi \left( x \right)$$
(23)

where \(P = \left[ {\bar{y}^{1} ,\bar{y}^{2} , \ldots ,\bar{y}^{M} } \right]^{T}\) is the adjustable parameter vector of the fuzzy system, and \(\xi \left( x \right) = \left[ {\xi_{1} \left( x \right),\xi_{2} \left( x \right), \ldots ,\xi_{M} \left( x \right)} \right]^{T}\) is the vector of fuzzy basis functions defined as below:

$$\xi_{l} \left( x \right) = \frac{{\mathop \prod \nolimits_{i = 1}^{n} \mu_{{A_{i}^{l} }} \left( {x_{i} } \right)}}{{\mathop \sum \nolimits_{l = 1}^{M} \left( {\mathop \prod \nolimits_{i = 1}^{n} \mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} \right)}}$$
(24)

According to the approximation property of adaptive fuzzy systems [37, 38], a continuous nonlinear function \(F\left( x \right)\) can be represented by adaptive fuzzy systems, i.e.,

$$F\left( {x,P} \right) = P^{T} \xi \left( x \right) + \varepsilon_{m}$$
(25)

where \(\varepsilon_{m}\) is the fuzzy approximation error.

4 The proposed controller

With the use of the independent joint method, the stability analysis becomes simpler [35]. Let us define the tracking error as \(e = q_{d} - q\). Using (12), we have

$$\ddot{e} = \ddot{q}_{d} - v + f$$
(26)

Now, define a sliding surface as

$$s\left( t \right) = \dot{e} + a_{1} e + a_{2} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau$$
(27)

In which \(a_{1}\) and \(a_{2}\) are positive constants. Taking the time derivative of (27), the following equation can be obtained

$$\dot{s}\left( t \right) = \ddot{e} + a_{1} \dot{e} + a_{2} e$$
(28)

Using (26), (28) can be expressed as

$$\dot{s}\left( t \right) = \ddot{q}_{d} - v + f\left( t \right) + a_{1} \dot{e} + a_{2} e$$
(29)

The secondary sliding surface is considered as

$$\sigma \left( t \right) = \dot{s} + c_{1} s + c_{2} \mathop \int \limits_{0}^{t} s\left( \tau \right)d\tau$$
(30)

In which \(c_{1}\) and \(c_{2}\) are positive constants. The time derivative of (30) becomes

$$\dot{\sigma }\left( t \right) = \ddot{s} + c_{1} \dot{s} + c_{2} s$$
(31)

Using (27) and (29), (31) can be written as

$$\dot{\sigma }\left( t \right) = (\dddot q_{d} - \dot{v} + \dot{f}\left( t \right) + a_{1} \ddot{e} + a_{2} \dot{e}) + c_{1} \left( {\ddot{q}_{d} - v + f\left( t \right) + a_{1} \dot{e} + a_{2} e} \right) + c_{2} \left( {\dot{e} + a_{1} e + a_{2} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau } \right)$$
(32)

Substitution of (26) into (32) yields

$$\begin{aligned} \dot{\sigma }\left( t \right) & = \dddot q_{d} - \dot{v} + \dot{f}\left( t \right) + a_{1} \left( {\ddot{q}_{d} - v + f} \right) + a_{2} \dot{e} + c_{1} \ddot{q}_{d} - c_{1} v + c_{1} f\left( t \right) + a_{1} c_{1} \dot{e} \\ & \quad + \,a_{2} c_{1} e + c_{2} \dot{e} + a_{1} c_{2} e + a_{2} c_{2} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau \\ & = \dddot q_{d} - \dot{v} + \left( {a_{1} + c_{1} } \right)\left( {\ddot{q}_{d} - v} \right) + \dot{f}\left( t \right) + \left( {a_{1} + c_{1} } \right)f\left( t \right) + (a_{2} + a_{1} c_{1} + c_{2} )\dot{e} \\ & \quad + \,\left( {a_{2} c_{1} + a_{1} c_{2} } \right)e + a_{2} c_{2} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau \\ \end{aligned}$$
(33)

We can rewrite (33) as

$$\dot{\sigma }\left( t \right) = \dddot q_{d} - \dot{v} + \lambda_{1} \varPsi \left( t \right) + g + \lambda_{2} \dot{e} + \lambda_{3} e + \lambda_{4} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau$$
(34)

where \(\varPsi \left( t \right) = \ddot{q}_{d} - v, g = \dot{f} + \lambda_{1} f, \lambda_{1} = a_{1} + c_{1} , \lambda_{2} = a_{2} + a_{1} c_{1} + c_{2} , \lambda_{3} = a_{2} c_{1} + a_{1} c_{2}\) and \(\lambda_{4} = a_{2} c_{2}\). The controller \(v\) is designed such that \(\dot{\sigma }\left( t \right) = 0\), then \(\ddot{s} + c_{1} \dot{s} + c_{2} s = 0\). Thus, \(s\left( t \right)\) converges to zero. By \(\dot{\sigma }\left( t \right) = 0\) and (34), we have [16]

$$\begin{aligned} & \dot{v}_{DSMC} = \dddot q_{d} + \lambda_{1} \varPsi \left( t \right) + \lambda_{2} \dot{e} + \lambda_{3} e + \lambda_{4} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau + \rho_{DSMC} sgn\left( {\sigma \left( t \right)} \right) \\ & v_{DSMC} \left( t \right) = \mathop \int \limits_{0}^{t} \dot{v}_{DSMC} \left( \tau \right)d\tau \\ & \left| g \right| < \rho_{DMSC} \\ \end{aligned}$$
(35)

Like conventional SMC, a trial and error technique is usually utilized to obtain the control gain \(\rho_{DSMC}\). In order to eliminate the term \(\rho_{DSMC} sgn\left( {\sigma \left( t \right)} \right)\) from (35), an adaptive dynamic sliding mode control (ADSMC) is proposed to replace \(\rho_{DSMC} sgn\left( {\sigma \left( t \right)} \right)\) by the uncertainty estimation \(\hat{g}\). This estimation can be obtained by fuzzy systems, Legendre polynomials or Fourier series. In this paper, their performances will be compared. Thus, the control law in ADSMC is given by

$$\begin{aligned} & \dot{v}_{ADSMC} = \dddot q_{d} + \lambda_{1} \varPsi \left( t \right) + \lambda_{2} \dot{e} + \lambda_{3} e + \lambda_{4} \mathop \int \limits_{0}^{t} e\left( \tau \right)d\tau + \hat{g} + v_{r} \\ & v_{ADSMC} \left( t \right) = \mathop \int \limits_{0}^{t} \dot{v}_{ADMSC} \left( \tau \right)d\tau \\ \end{aligned}$$
(36)

where \(\hat{g}\) is estimated value of \(g\) using fuzzy systems, Legendre polynomials or Fourier series and \(v_{r}\) is the continuous robust control term to compensate the approximation error. One can represent \(g\left( t \right)\) as linear combinations of basis functions \(\xi\) as

$$g\left( t \right) = P^{T} \xi + \varepsilon$$
(37)

where \(P\) is weighting vector, and \(\varepsilon\) is the approximation error. Now, making use of the same set of basis functions, we propose

$$\hat{g}\left( t \right) = \hat{P}^{T} \xi$$
(38)

The basis functions can be fuzzy basis functions, Legendre polynomials or sinusoidal functions in Fourier series. Also, the weighting vector can be the adjustable parameters of the fuzzy system in the consequent part of the fuzzy rules, Legendre coefficients or the Fourier series coefficients. It follows from (34) and (36) that

$$\dot{\sigma } = g - \hat{g} - v_{r}$$
(39)

Using (37) and (38), we can write

$$\tilde{g} = g - \hat{g} = P^{T} \xi + \varepsilon - \hat{P}^{T} \xi = \left( {P - \hat{P}} \right)^{T} \xi + \varepsilon_{m} = \tilde{P}^{T} \xi + \varepsilon_{m}$$
(40)

As a result, (40) can be rewritten as

$$\dot{\sigma } = \tilde{P}^{T} \xi + \varepsilon_{m} - v_{r}$$
(41)

The sampling interval in the experiment is short enough as compared with the variation of \(\varepsilon_{m}\), thus, the term \(\varepsilon_{m}\) is assumed to be a constant during the estimation (i.e.\(\tilde{\varepsilon }_{m} = \varepsilon_{m} - \hat{\varepsilon }_{m} \to \dot{\tilde{\varepsilon }}_{m} = - \dot{\hat{\varepsilon }}_{m}\)) [39,40,41].

5 Stability analysis

Usually, the adaptation laws for online adjustment of \(\hat{P}\), include a constant parameter, for instance \(\gamma\), called as convergence rate which plays an important role in reducing the tracking error. However, increasing \(\gamma\) may result in initial high control effort if there is an initial tracking error. To solve this problem, it has been assumed that \(\gamma\) is given by an increasing time-varying function.

Assumption 1

The convergence rate \(\gamma\) is given by

$$\gamma \left( t \right) = \left( {\gamma_{0} - \gamma_{f} } \right)exp \left( { - \beta t} \right) + \gamma_{f} , \gamma_{f} > \gamma_{0} > 0$$
(42)

where \(\gamma_{0}\) and \(\gamma_{f}\) are initial and final values of \(\gamma \left( t \right)\) and \(\beta\) is a positive constant parameter.

Theorem 1

If the following rules are applied to the system (12) and the control law (36), then the closed loop signals are bounded and the tracking error asymptotically converges to zero.

$$\dot{\hat{P}} = \gamma \left( t \right)\sigma \left( t \right)\xi$$
(43)
$$v_{r} = k_{p} \sigma \left( t \right) + \hat{\varepsilon }_{m}$$
(44)
$$\dot{\hat{\varepsilon }} = k_{I} \sigma \left( t \right)$$
(45)

where \(k_{p}\) and \(k_{I}\) are positive scalars and \(\gamma \left( t \right)\) is given by (42).

Proof

Consider the following positive definite function

$$V = \frac{{\sigma^{2} \left( t \right) }}{2} + \frac{{\tilde{P}^{T} \tilde{P}}}{2\gamma \left( t \right)} + \frac{{\tilde{\varepsilon }_{m}^{2} }}{{2k_{I} }}$$
(46)

where \(\tilde{\varepsilon }_{m} = \varepsilon_{m} - \hat{\varepsilon }_{m}\) and \(\tilde{P} = P - \hat{P}\). Differentiating \(V\) with respect to time, we have

$$\dot{V} = \sigma \dot{\sigma } - \frac{{\tilde{P}^{T} \dot{\hat{P}}}}{\gamma \left( t \right)} - \frac{{\dot{\gamma }\left( {\tilde{P}^{T} \tilde{P}} \right)}}{{2\gamma^{2} \left( t \right)}} - \frac{{\tilde{\varepsilon }_{m} \dot{\hat{\varepsilon }}_{m} }}{{k_{I} }}$$
(47)

Using (41), we can write

$$\dot{V} = \sigma \left( {\tilde{P}^{T} \xi + \varepsilon_{m} - v_{r} } \right) - \frac{{\tilde{P}^{T} \dot{\hat{P}}}}{\gamma \left( t \right)} - \frac{{\dot{\gamma }\left( {\tilde{P}^{T} \tilde{P}} \right)}}{{2\gamma^{2} \left( t \right)}} - \frac{{\tilde{\varepsilon }_{m} \dot{\hat{\varepsilon }}_{m} }}{{k_{I} }}$$
(48)

Using (44), we can write

$$\dot{V} = \sigma \left( {\tilde{P}^{T} \xi + \tilde{\varepsilon }_{m} - k_{p} \sigma \left( t \right)} \right) - \frac{{\tilde{P}^{T} \dot{\hat{P}}}}{\gamma \left( t \right)} - \frac{{\dot{\gamma }\left( {\tilde{P}^{T} \tilde{P}} \right)}}{{2\gamma^{2} \left( t \right)}} - \frac{{\tilde{\varepsilon }_{m} \dot{\hat{\varepsilon }}_{m} }}{{k_{I} }}$$
(49)

Using (43), (49) is simplified to

$$\dot{V} = \sigma \left( {\tilde{\varepsilon }_{m} - k_{p} \sigma \left( t \right)} \right) - \frac{{\dot{\gamma }\left( {\tilde{P}^{T} \tilde{P}} \right)}}{{2\gamma^{2} \left( t \right)}} - \frac{{\tilde{\varepsilon }_{m} \dot{\hat{\varepsilon }}_{m} }}{{k_{I} }}$$
(50)

Also, using (45), (50) is simplified to

$$\dot{V} = - k_{p} \sigma^{2} \left( t \right) - \frac{{\dot{\gamma }\left( {\tilde{P}^{T} \tilde{P}} \right)}}{{2\gamma^{2} \left( t \right)}}$$
(51)

According to (42), \(\dot{\gamma }\) is calculated as

$$\dot{\gamma } = - \beta \left( {\gamma_{0} - \gamma_{f} } \right)exp \left( { - \beta t} \right)$$
(52)

Using Assumption 1, it follows that \(\dot{\gamma }\) is positive and consequently \(\dot{V}\) in (51) is negative semidefinite. Therefore, \(V\left( {\sigma \left( t \right),\tilde{P}\left( t \right),\tilde{\varepsilon }_{m} \left( t \right)} \right) \le V\left( {\sigma \left( 0 \right),\tilde{P}\left( 0 \right),\tilde{\varepsilon }_{m} \left( 0 \right)} \right)\) [42] which implies that \(\sigma\), \(\tilde{p}\) and \(\tilde{\varepsilon }_{m}\) are bounded. Define \(\varOmega \left( t \right) = k_{p} \sigma^{2} \left( t \right) \le - \dot{V}\). Integrating \(\varOmega \left( t \right)\) with respect to time yields

$$\mathop \int \limits_{0}^{t} \varOmega \left( \tau \right)d\tau \le V\left( {\sigma \left( 0 \right),\tilde{P}\left( 0 \right),\tilde{\varepsilon }_{m} \left( 0 \right)} \right) - V\left( {\sigma \left( t \right),\tilde{P}\left( t \right),\tilde{\varepsilon }_{m} \left( t \right)} \right)$$
(53)

Because \(V\left( {\sigma \left( 0 \right),\tilde{P}\left( 0 \right),\tilde{\varepsilon }_{m} \left( 0 \right)} \right)\) is bounded, and \(V\left( {\sigma \left( t \right),\tilde{P}\left( t \right),\tilde{\varepsilon }_{m} \left( t \right)} \right)\) is nonincreasing and bounded, the following result is obtained:

$$lim_{t \to \infty } \mathop \int \limits_{0}^{t} \varOmega \left( \tau \right)d\tau < \infty$$
(54)

By utilizing Barbalat’s lemma [42], we obtain \(lim_{t \to \infty } \varOmega \left( t \right) = 0\). As a result, \(\sigma \left( t \right)\) will converge to zero which implies that \(s\left( t \right)\) and consequently the tracking error \(e\left( t \right)\) converge to zero. According to a proof presented in [5], the motor voltage is bounded, i.e. \(\left| {v_{ADMSC} } \right| \le v_{max}\), thus, \(\dot{q}\) and \(I_{a}\) are bounded. Therefore, state variables \(X\) in (5) are bonded.

To summarize, Fig. 1 shows the overall approach of the adaptive dynamic sliding mode control proposed in this paper.

Fig. 1
figure 1

Overall approach of the proposed adaptive dynamic sliding mode controller

Full size image

6 Simulation results

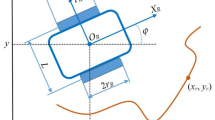
To show the effectiveness of the proposed method, it is applied to a SCARA robot driven by permanent magnet dc motors. The parameters of robotic system are given in [29]. A symbolic representation of the manipulator is illustrated in Fig. 2. The maximum voltage of each motor is set to \(v_{max} = 50 \,{\text{V}}\). The desired trajectory should be sufficiently smooth such that all its derivatives up to the required order are bounded. The desired position for every joint is given by

Fig. 2
figure 2

Symbolic representation of the SCARA manipulator

Full size image
$$q_{d} = 1 - \cos \left( {\pi t /10} \right)$$
(55)

The external disturbance is inserted to the inputs at \(t = 5 \,{\text{s}}\) as a step function with the amplitude of 3 V. The sliding surface parameters have been chosen as \(a_{1} = 20,a_{2} = 0.2, c_{1} = 10, c_{2} = 0.1\). The initial joint positions have been selected as \(q\left( 0 \right) = - 0.2\). The parameters \(k_{p}\) and \(k_{I}\) have been set to the values of 1 and 10, respectively. Simulation 1 investigates the influence of convergence rate on the tracking error and control efforts. It has been assumed that the lumped uncertainty is estimated using adaptive fuzzy system. The characteristics of the fuzzy system are the same as explained in [17]. In other words, in (37), the vector \(\xi\) is calculated based on fuzzy membership functions. Simulation 2, compares the performances of different uncertainty estimators.

6.1 Simulation 1: the effect of convergence rate on the controller performance

In this simulation, the effect of convergence rate is investigated. Three cases have been considered as

$${\text{Case}}\;1{:}\quad \gamma \left( t \right) = 10$$
(56)
$${\text{Case}}\;2{:}\quad \gamma \left( t \right) = 1000$$
(57)
$${\text{Case}}\;3{:}\quad \gamma \left( t \right) = \left( {10 - 1000} \right)e^{ - 0.2t} + 1000$$
(58)

As shown in Fig. 3, the tracking error for Case 1 is not acceptable, since \(\gamma \left( t \right)\) is small. Although, the tracking error for Case 2 in Fig. 4 is satisfactory, the control efforts at initial times are not acceptable as shown in Fig. 5. In fact, in case 2, due to large convergence rate, the tracking errors are good. Nevertheless, this large convergence rate results in actuator saturation and chattering phenomenon. The proposed convergence rate for Case 3 has solved the trade-off problem between accuracy and control effort. According to Fig. 6, the tracking error is acceptable. Also, as illustrated in Fig. 7, the control signal does not reach to saturation region at initial times. The proposed convergence rate is small at initial times to prevent from actuator saturation and the chattering phenomenon. To make the steady state tracking error as small as possible, the convergence rate is gradually increased.

Fig. 3
figure 3

The tracking errors in Simulation 1 for case 1

Full size image
Fig. 4
figure 4

The tracking errors in Simulation 1 for case 2

Full size image
Fig. 5
figure 5

The control signals in Simulation 1 for case 2

Full size image
Fig. 6
figure 6

The tracking errors in Simulation 1 for case 3

Full size image
Fig. 7
figure 7

The control efforts in Simulation 1 for case 3

Full size image

6.2 Simulation 2: comparison between different uncertainty estimators

Suppose that instead of fuzzy systems, the Fourier series is used for uncertainty estimation. In other words, the vector \(\xi\) is in the form of [1, 29, 30]

$$\xi = \left[ {\begin{array}{*{20}c} 1 & {\cos \left( {\pi t/10} \right)} & {\sin (\pi t/10} \\ \end{array} } \right]^{T}$$
(59)

In the case of using Legendre polynomials for uncertainty estimation, the vector \(\xi\) is in the form of [28, 31]

$$\xi = \left[ {\begin{array}{*{20}c} 1 & x & {\begin{array}{*{20}c} {\frac{1}{2}\left( {3x^{2} - 1} \right)} & {\frac{1}{2}\left( {5x^{3} - 3x} \right)} \\ \end{array} } \\ \end{array} } \right]^{T}$$
(60)

In which \(x = \sin \left( {\pi t/10} \right)\). In order to have a quantitative comparison, consider the criterion \(Fitness = \mathop \int \nolimits_{0}^{10} \left[ {\mathop \sum \nolimits_{i} e_{i}^{2} } \right]dt\) [43,44,45,46,47,48,49,50,51,52]. All the controller parameters are the same as those presented in simulation 1. The convergence rate given in Case 3 is selected in this simulation for all uncertainty estimators. The criterion for the fuzzy system, Fourier series and Legendre polynomials is 0.0368, 0.0251 and 0.0289, respectively. Thus, it seems that Fourier series outperforms the others. The tracking error for the Fourier series is illustrated in Fig. 8. As shown in this figure, tracking errors reduce as fast as possible and after the transient state is terminated at \(t = 2 \,{\text{s}}\), the tracking errors are around − 0.001. In addition, the effect of external disturbance is negligible on this controller. The control efforts using the Fourier series are presented in Fig. 9. In comparison with Fig. 7 (fuzzy system), although motor voltages are larger in the transient state, they do not exceed the permitted range. In fact, these larger voltages in the Fourier series expansion have resulted in smaller tracking errors.

Fig. 8
figure 8

The tracking errors in Simulation 2 using the Fourier series expansion

Full size image
Fig. 9
figure 9

The control signals in Simulation 2 using the Fourier series expansion

Full size image

The tracking error for Legendre polynomials is illustrated in Fig. 10. As shown in this figure, tracking errors reduce as fast as possible and after the transient state is terminated at \(t = 3 \,{\text{s}}\), the tracking errors are around − 0.001. In comparison with Fig. 8 (Fourier series expansion), it seems that the transient state for Legendre polynomials is longer. The effect of external disturbance on this controller is also small. The control efforts using Legendre polynomials are presented in Fig. 11. Motor voltages for Legendre polynomials in this figure are similar to those illustrated in Fig. 9. However, it seems that after applying the external disturbance at \(t = 5 sec\), the Fourier series expansion has a smoother performance.

Fig. 10
figure 10

The tracking errors in Simulation 2 using Legendre polynomials

Full size image
Fig. 11
figure 11

Control signals in Simulation 2 using Legendre polynomials

Full size image

Remark

It is obvious that increasing \(k_{p}\) will increase the amplitude of the control signal. For example, if \(k_{p} = 15\), actuator saturation will occur. Also, decreasing the parameter \(k_{I}\) will deteriorate the tracking performance and the performance criterion will increase. For the sliding surface parameters \(a_{1}\) and \(c_{1}\), small values such as 2 or 1 will result in poor tracking performance and the convergence of the tracking error will occur after even 10 s. Selecting large values for \(a_{2}\) and \(c_{2}\), will deteriorate the tracking performance and the control signal will increase.

Finally, the system performance in the presence of white noise is studied. It has been assumed that the position and velocity signals are contaminated by noise. The noise signal is presented in Fig. 12 [53]. The proposed estimator in this section is the Fourier series expansion with exponential convergence rate. The tracking errors and the voltage signals are plotted in Figs. 13 and 14, respectively. As shown in Fig. 13, the tracking error reduces to small values and its mean in the steady state is around zero. Also, the control signal illustrated in Fig. 14 is acceptable. In fact, the noisy signals cannot deteriorate the voltage signal profile considerably.

Fig. 12
figure 12

The profile of noise signal

Full size image
Fig. 13
figure 13

The tracking errors using the Fourier series expansion in the presence of noise

Full size image
Fig. 14
figure 14

The control signals using the Fourier series expansion in the presence of noise

Full size image

7 Conclusion

In this paper, an adaptive control scheme for robotic systems using uncertainty estimators with exponential convergence rate has been presented. For chattering eliminating in dynamic sliding mode control, the lumped uncertainty has been estimated using various estimators such as fuzzy systems, Legendre polynomials and Fourier series expansion. As a result, there is no need to obtain the upper bound of uncertainty using the tedious trial and error procedure. Moreover, the convergence rate of the estimators has been gradually increased in order to prevent from actuator saturation at initial times. In comparison with constant convergence rates, the proposed convergence rate results in a superior performance. Moreover, a comparison between fuzzy systems, Legendre polynomials and Fourier series expansion has been performed that verifies the superiority of Fourier series.

8 Future recommendation

Future works in this field can be designing observer for dynamic sliding mode control. Also, the performance of the proposed controller on flexible joint robots can be studied. In addition, optimization techniques can be examined for tuning the controller parameters to improve its performance.