A hierarchical threshold modeling approach for understanding phenological responses to climate change: when did North American lilacs start to bloom earlier?

Abstract

Prior to the recent upward climb, global average temperatures were relatively stable. This trend was described by Mann et al. [23] using a hockey-stick model consisting of two line segments (with the x-axis as time and temperature as the y-axis) meeting at a single changepoint. The line segment prior to the changepoint is flat (indicating a stable temperature), and the line after the changepoint has a positive slope (indicating increasing temperatures). Because the long-term average temperature change is a defining characteristic of climate change, researchers have shown that changes in many phenological variables over time can also be described by a hockey-stick model. For phenological variables, the changepoint and the slope of the line after the changepoint represent the timing of the onset and the effect of climate change. However, large annual variation often obscures the pattern when analyzed using data from a single location, whereas regional differences due to spatial variability of climate and weather patterns render pooling data from different locations impractical. We demonstrate that the Bayesian hierarchical modeling approach is effective in separating these two sources of variability by partially pooling data from multiple sites. Using the North American lilac first bloom dates, we show that the Bayesian approach can adequately separate the temporal and spatial variations, thereby quantify site-specific patterns of change as well as national/regional average trends. Our analysis, using the Bayesian hierarchical hockey-stick model, showed that the effects of climate change started as early as the 1970s and the lilacs in North America have been blooming on average one day earlier every three years since.

Introduction

Global average temperatures were relatively constant, with some annual variation, from the early 1800s to approximately the mid-twentieth century prior to a sharp increase after the mid-twentieth century (Intergovernmental Panel on Climate Change (IPCC), Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 2014 [19, 23]. The global average temperature has increased by 0.67 degrees Celsius since 1986, surpassing the recorded increase in the 59 year period prior to 1986 [17]. This pattern of global average temperature change was described by Mann et al. [23] using a hockey-stick graph. In this study, Mann et al. [23] depicted a recent changepoint, within the past century, in the increased occurrence of temperature anomalies. The hockey-stick model is characterized by a flat left line segment and a sloped right line segment that meet at a changepoint (Fig. 1).

Fig. 1

General graphical form of the hockey-stick model. The x-axis is year and the y-axis is the response, typically the ordinal day of the phenological trend, an example would be the day of year of the peak bloom of Washington D.C. cherry blossoms. The variable α is the left line segment y-intercept showing day of year of trend prior to the changepoint. For example, Washington D.C. cherry blossoms consistently have a peak bloom on day 95 or about April 5 prior to the changepoint. The variable β is the slope of the right line segment showing the rate of change in response after the changepoint, which would be about 1/7th of a day earlier each year in the case of Washington D.C. cherry blossom peak bloom dates. Lastly, ϕ is the changepoint where the two line segments meet indicating the onset of climate change effects, in the case of Washington D.C. cherry blossom peak bloom dates this is about 1965

Because temperature is a key feature of climate change, many phenological phenomena respond to climate change in a similar pattern that can also be represented by the hockey-stick model [11, 36]. For example, Qian [30] used the hockey-stick model to describe the temporal changes in the first bloom dates of North American lilacs, showing that lilacs have bloomed earlier in recent years based on multiple graphs with the day-of-the-year on the y-axis and year on the x-axis. Additionally, Dose and Menzel [11] applied three different models to the flowering dates of Cherry blossom, Snow drop blossom, and Lime tree blossoms. They concluded that the hockey-stick, or changepoint, model best represented the phenological data examined [11]. A similar analysis was conducted on common plant species located several parts of Europe by Schleip et al. [36]. This study found the comparable results to Does and Menzel [11], showing that a hockey-stick model explained the phenological phenomena more than any other model explored (Shleip et al. 2009). The research from Qian [30], Dose and Menzel [11], and Shleip et al. [36] shows that while the hockey-stick model is a simplification of complex processes, it resembles the pattern observed in data well and provides more useful information than a traditional linear model does. The hockey-stick trend observed in phenological phenomena is reasonable because the rise in global greenhouse gas concentrations, the mechanism that underlies the rise in global temperature, follows a pattern summarized by the hockey-stick model: a relatively constant trend rapidly transitioning to a steep rising trend (Supplemental Fig. 1 available at GitHub.com/StephAnnieNummer/Lilac_HockeyStick_BHM, [26]). This rise in global temperature in recent years can be attributed to the increase in greenhouse gasses from anthropogenic sources since the mid-1800s [26].

Other events also experience changes induced by the recent changes in temperature due to the increase in greenhouse gas concentrations in the atmosphere. Hayhoe et al. [17] reported changes in temperature extremes associated with the global temperature increase, including surges in heat and cold wave frequencies. Phenological events throughout the world are experiencing changes in association with the increase in global average temperature as well [1, 9, 43]. Ahas et al. [1] examined the phenological shifts of six different plant species in Europe in response to changes in climate and temperature and found that areas with snow coverages are presenting with the greatest change. Additionally, Walther et al. [43] compiled evidence of ecological response to climate change including shifts in bird breeding and migration, earlier butterfly appearances, changes in the spawning of amphibians, and earlier trends in plant phenology. Chen [9] examined and reviewed phenological events across different regions in China and found shifts including changes in green-up dates and first leaf unfolding dates.

Several examples of these phenological shifts and phenomena have been the subject of research. Bird populations are declining or are at risk of declining because food availability is peaking earlier than when the birds arrive due to the warming temperature [4]. This change in peak food availability is a potential driver for bird breeding season to shift earlier. Cherry blossom blooming is an iconic Washington D.C. event, and this city has an almost century-long record of cherry blossom peak bloom dates. This dataset illustrates a shift in the peak bloom dates of these cherry trees (Fig. 2). Furthermore, Mason et al. [24] found that the duration of Great Lakes ice coverage has decreased. Great Lakes ice cover duration, mismatch between bird migration and food availability, and the Washington D.C. cherry blossom peak bloom dates are just a few examples of a large body of evidence of phenological shifts [1, 5, 28, 35, 37, 43].

Fig. 2

Hockey-stick model developed by Qian [30] applied to Washington, D.C. cherry blossoms peak bloom dates from 1930 to 2016. The vertical indicates the changepoint of 1964.9 (1930.3, 1999.6). The slope after the changepoint is −0.13 (−0.001, −0.25) days earlier per year after 1964.9

North American lilacs first bloom dates are another phenological event that responds to the change in global average temperature. Schwartz [38] found that phenological data, including North American lilac first bloom dates, can be used as a missing link for satellite observations and thus adds to the need for cooperative research efforts to understand ecological questions. Schwartz et al. [40] used the North American lilac first bloom dates as an example of this cooperative research efforts because it is one of the first extensive phenological datasets in the USA. Schwartz and Reiter [41] and Wolfe et al. [44] analyzed portions of the North American lilac first bloom data using a linear model and found a shift of 0.14 and 0.092 days earlier each year in first bloom dates, respectively. Earlier blooming of North American lilacs was identified by Cayan et al. [8] using a linear model while Brunsdon and Comber [5] used a multilevel modeling to find a similar trend. Recently, Gerst et al. [16] evaluated Spring Indices applied to North American lilac and honeysuckle phenological data by Schwartz et al. [39] and concluded that these indices are generally a good proxy of observed phenological phenomena in North American lilacs and honeysuckle.

The typically used linear model for phenological studies (e.g., [1, 17] almost always underestimates the magnitude of change when the data include observations made before the onset of climate change effect [30]. Instead, research shows that a hockey-stick model explains phenological data better than a traditional linear regression by avoiding potential overestimation prior to the onset of climate change and underestimation after the onset of climate change [11, 28, 35]. A hockey stick model (or piecewise linear model) can be computationally challenging because of the discontinuity in its first derivatives. An early solution to the difficulty is to introduce smooth connection between the two intersecting line segments [2]. This approach is implemented in Qian [30]. However, using nonlinear regression requires appropriate starting values for all coefficients, a tedious trial and error process. Although Bayesian method is often computationally more intensive, the use of Markov chain Monte Carlo simulation made these computations trackable [32]. Consequently, we propose the use of the hockey-stick model as a modeling framework to describe the general pattern of temperature-sensitive phenomena or events in response to climate change.

Using a hockey-stick model, we can better describe the basal mechanisms, or forcing function, that led to the changes occurring in the phenological variable of interest, as well as the underlying pattern of long-term global average temperature change. The model provides two key parameters that can help us retrospectively estimate the time when the effect of climate change initiated and the magnitude of the change. These two key parameters are the changepoint which represents when the impacts of climate change on the phenological response began and the slope of the line after the changepoint which shows the rate at which the response is changing. We used Bayesian computational method to expand the model to include data from multiple locations.

The two key parameters of the hockey-stick model can lend more information to researchers and better describe phenological data than a traditional linear model [11, 28, 35]. Does and Menzel [11] found that the one-changepoint model (i.e., hockey-stick model) was the optimal model for the application to phenological data. A further understanding of this was provided by, Schleip et al. [35] who compared a constant, linear, and hockey-stick model. The hockey-stick model represented the pattern of phenological data the best. In addition, Pope et al. [28] found the hockey-stick model ideal for modeling the spring response of phenological data. Qian [30] developed an R function that easily fit the hockey-stick model. When applied to North American lilac first bloom dates from four Pacific Northwest locations, the estimated changepoints range from 1974 to 1983 [30]. The same model showed that the climate change effect on Washington, D.C. cherry blossom likely started as early as mid-1960 s and the peak bloom date has since moved about 6–7 days earlier (Fig. 2).

Phenological data, such as first bloom dates of the North American lilac, are inevitably location-specific because weather and climate patterns vary geographically [5]. As such, combining phenological data from different locations are unadvisable and we typically analyze these data by location. However, phenological data from a single location are almost always noisy because of the natural variation in weather. Due to this natural variation in day-to-day and year-to-year weather, we may not be able to see the hockey-stick pattern clearly, just as the long-term mean temperature signal [3]. Thus, accurately depicting the underlying pattern requires a long-term record at a single location. Even with the century-long Washington D.C. cherry blossom data, fitting a hockey-stick model is still unconvincing compared to a simple linear model. Brunsdon and Comber [5] proposed using the multilevel modeling approach that applies the intended model to each group, often geographic location, and partially pool all groups together to improve statistical power [15, 30]. The application of a multilevel, or Bayesian hierarchical, modeling approach provides a practical means to reduce site-specific estimation uncertainty through partially pooling the data from multiple locations [5, 15].

While research has documented when changes in global temperature began to impact phenological responses, this research typically follows one of two approaches: (1) employing a linear regression while using a multilevel model [5, 10] or (2) applying a hockey-stick model to the data from all locations together as one [35]. The goal of our research is to combine these two methods by developing a Bayesian hierarchical hockey-stick model for partially pooling phenological data from multiple locations to better differentiate region-specific patterns of response, as well as the aggregated response pattern.

The general premise of a Bayesian hierarchical modeling approach can be traced back to Stein’s paradox and empirical Bayes methods, which reduces overall estimation uncertainty by partially pooling information from similar observations made in multiple locations (see [12] for an extensive review and [33] for recent references). Although the computational complexity of applying the hockey-stick model [32] to data from a single location is no longer an issue [30], a stable maximum likelihood estimator of a multilevel hockey-stick model is still unavailable. Consequently, we opt to use the Bayesian computational method via Markov chain Monte Carlo simulation. The North American lilac phenological dataset, compiled by Schwartz and Reiter [41], includes annual first bloom and leaf dates for the common lilac (Syringa vulgaris) from 1956–2003 and collected at 1126 locations across North America. This well-studied dataset is ideal for our study because of its long-term records, availability, and large areal coverage [5, 8, 41]. The Bayesian hierarchical hockey-stick model in this study will bring together both the suggested model for phenological data and the need for a hierarchical structure to organize the data from different locations. By using this model, we can quantify when biological systems began to respond to the change in global average temperature and the rate at which they are responding, both at individual locations and at a continental scale.

Methods

Hockey-stick model

The hockey-stick model consists of two line segments that meet at a changepoint. On the left of the changepoint, the line is flat, indicating the stable trend prior to the change in phenological response. The line to right of the changepoint is characterized by a positive or negative slope that describes the phenological trend occurring in response to changes in global average temperature. These line segments meet at the changepoint, indicating when the system began to respond to climate change. The formula of the hockey-stick model applied in this study is

$$y_{i} = \left\{ {\begin{array}{*{20}c} {\alpha + \varepsilon _{1} ,\quad x_{i} < \phi } \\ {\alpha + ~\beta \left( {x_{i} - \phi } \right) + \varepsilon _{2} ,\quad x_{i} \ge \phi } \\ \end{array} } \right.$$

(1)

where y_i is the response measured in day of year, α is the intercept of the left line segment (representing the average response before the effect of climate change on the response can be detected through the model), β is the slope of the right line segment (representing the average annual change of the response since the effect of climate change on the response became detectable), x_i is the calendar year, ϕ is the changepoint where the two line segments meet (the year when climate change effect on the response become detectable), and ε₁ and ε₂ are the error terms associated with the model (representing the annual variability of the response variable) and assumed to be normal random variables with a constant variance ε₁ ~ N(0, σ₁²) and ε₂ ~ N(0, σ₂²). This model specification allows the two error terms, ε₁ and ε₂, to have different variances. While this is available, we assume that the two error terms share the same variance in our study. In the case of North American lilac first bloom dates, the intercept $\alpha$ is the average day of year of the first bloom before the effect of climate change can be detected. The slope β represents the average rate, that is, days per year that lilacs are blooming earlier. Finally, the changepoint, ϕ, is when lilacs first appeared to respond to the effect of climate change.

Bayesian hierarchical implementation

The Bayesian hierarchical hockey-stick model is a computational method we used to pool data from different locations to simultaneously fit location-specific models and an “average” model [15]. This method fits the hockey-stick model to all locations at the same times as opposed to one at a time, as is with Eq. 1. The functional form of the Bayesian hierarchical hockey-stick model is the same as the single-location hockey-stick model, but with location-specific model coefficients:

$$y_{{ij}} = \left\{ {\begin{array}{*{20}c} {\alpha _{j} + \varepsilon _{{1j}} ,~\quad x_{i} < \phi _{j} } \\ {\alpha _{j} + ~\beta _{j} \left( {x_{i} - \phi _{j} } \right) + \varepsilon _{{2j}} ,\quad ~x_{i} \ge \phi _{j} } \\ \end{array} } \right.$$

(2)

where the subscript j represents locations. The changepoint, ϕ, for each location is limited by the first and last year of monitoring for that group. As such, the changepoint cannot be outside the range of data when monitoring occurred for each location. If the change occurred before the first year or after the last year of the record, the estimated changepoint would be concentrated on one or the other end of the time record. The site-specific parameters are assumed to be exchangeable – these parameters vary by site and are otherwise uncertain. As a result, a common prior distribution is used:

$$\left( {\begin{array}{*{20}c} {\alpha_{j} } \\ {\beta_{j} } \\ {\varphi_{j} } \\ \end{array} } \right) \sim N\left( {\begin{array}{*{20}c} {\mu_{\alpha } } \\ {\begin{array}{*{20}c} {\mu_{\beta } } \\ {\mu_{\phi } } \\ \end{array} } \\ \end{array} , {\Sigma }} \right)$$

(3)

which is a multivariate normal distribution with mean μ_α, μ_β, μ_ϕ and variance–covariance matrix, Σ. These parameters are known as hyperparameters. Combining Eqs. (2) and (3), we estimate all model coefficients (site-specific intercept, slope, change-point, and the hyperparameters) simultaneously using Markov chain Monte Carlo simulation implemented in Stan [42] through R [34]. Computer code is available at GitHub.com/StephAnnieNummer/Lilac_HockeyStick_BHM.

Example data description

The North American lilac phenological dataset is a compilation of two separate observational studies performed by a network of volunteers ranging from 1956 to 2003 [41]. The first observational dataset began in the Western USA between 1956 and 1957 [6, 8]. Between 1961 and 1965 the second observational dataset began in the Eastern United States, with locations in Eastern Canada as well [40]. For both datasets, the first bloom and leaf dates are recorded as the ordinal day or day of the year, with January 1 being day 1. In this application, the response variable is the day of the year (ordinal date) of lilac first bloom date. Stations are assumed to be exchangeable with respect to model coefficients, thus allowing for the comparison between different stations and addressing the potential confounding factors due to location. Data from 53 stations with records of at least 30 years are used in our study (Fig. 3; the location of the 53 stations can be found in Supplemental Table 1), as we are interested in the long-term trends in response to the changes in temperature associated with the global rise in greenhouse gasses.

Fig. 3

Map of North America and the 53 stations that have at least 30 years’ worth of data in the North American lilac phenological dataset. The blue diamond is station 49,122 located near the South Cow Mountain OHV Recreation Area in California, USA. This station has the earliest changepoint and the steepest slope after the changepoint. Station 213,303 is the purple triangle and is located near Grand Rapids, Minnesota, USA, and has the shallowest slope of the right line segment and the latest changepoint

Results

The estimated hyperparameters for the entire dataset show a North American average changepoint (μ_ϕ) of 1972.9 (with a 95% credible interval of 1970.3, 1976.4), an average left line segment y-intercept (μ_α) of day 134.6 (129.8, 139.4) of the year, and an overall average right line segment slope (μ_β) of −0.37 (−0.46, −0.30) days per year (Fig. 4, Table 1). These estimated hyperparameters suggest that on average North American lilacs have started to bloom earlier since about 1973. Prior to 1973 North American lilacs typically bloomed on approximately day 135, or about May 15th, each year. Since 1973, North American lilac first bloom dates shift earlier by about one day for every three years. The estimated average rate of change is about double of the estimated rate of change found by Brunsdon and Comber [5] who used a linear multilevel model (−0.18 days per year).

Fig. 4

Bayesian hierarchical hockey-stick model for the 53 stations used from the North American lilac phenological dataset. The bold line represents the overall average and the model described by the hyperparameters. The light gray lines represent each station and the model described by station-level coefficients

Table 1 Hyperparameters and associated credible intervals for the 3 coefficients (ϕ – the time of climate change effect started, β – the rate of change since the onset of climate change effects, and α – average first bloom date before the onset of climate change effects) in the Bayesian hierarchical hockey-stick model

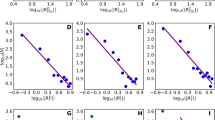
In addition to calculating the overall average for all stations, the Bayesian hierarchical model produced coefficients for each individual station (Fig. 4). All 53 stations included in this model have a changepoint that ranges between 1964.4 and 1976.4 and a right line segment slope between the range of −0.16 and −0.63 days per year (Fig. 5). While the credible intervals for each station show wide variation, we cannot directly compare the credible interval of individual stations to discern a significant difference because of the correlations among the estimated site-specific changepoints [29]. The earliest response was from station 49,122 which has a changepoint of 1964.4 (1957.8, 1973.2) and the steepest slope of the right line segment at −0.68 (−1.01, −0.38) days per year. Station 49,122 is located in California, USA, near South Cow Mountain OHV Recreation Area, while station 213,303 near Grand Rapids, Minnesota, USA, had the latest changepoint of 1976.4 (1973.1, 1986.3) and the shallowest slope of −0.16 (−0.40, −0.09) days per year.

Fig. 5

Changepoint, ϕ, and the right line segment slope, β, for each of the 53 stations used from the North American Lilac phenology dataset. The y-axis for each graph is organized to go from the most northern latitude at the top to the most southern latitude at the bottom. Each station had the estimated parameter as the bold dot with the 95% credible interval symbolized by the horizontal line

Discussion

Long-term change in average temperature is orders of magnitude smaller than the daily, seasonal, or year-to-year temperature variations. As a result, phenological signals often present with a weak or subtle trend e.g., changing fractions of a day per year, [41, 44] and can cause additional difficulties beyond those associated with the complex computations used in a multilevel model. In addition, large variation may be present in phenological data from a single location due to the noise associated with daily weather patterns. By pooling data from multiple locations, location-specific model coefficients are constrained by the overall average coefficients, thereby reducing overall estimation uncertainty [14] induced by large daily weather variations. The Bayesian hierarchical model is a shrinkage estimator, which always outperforms its non-shrinkage competitors [14, 25].

While the model used in this study was developed using the common lilac in North America, it is readily applicable for any long-term phenological data. For example, long-term crop yield data reported by Schlenker and Roberts [37] can be reanalyzed to examine the effect of climate change, in addition to the effect of temperature. Data presented by He et al. [18] can also be re-examined with the hockey-stick model to quantify the timing and magnitude of climate change because it is a long-term soybean phenology dataset shown to be influenced largely by temperature. Specifically, the soybean phenology examined by He et al. [18] include sowing, emergence, anthesis, and maturity. Applications studying the shift in the agricultural growing season can inform managers and farmers on how to better adapt for climate change.

Because the hierarchical model simultaneously estimates site-specific and overall average model parameters, the model is useful for both national and regional entities. At the local level, changes specific to the location (e.g., the rapid response to climate change in lilac first bloom dates near station 49,122) can inform managers to adjust monitoring schedule. At the national level, the estimated hyperparameters can inform government officials about the change and variation occurring at a national scale.

Although we fit the hockey-stick model by assuming the sites are exchangeable with respect to model coefficients, a scientifically meaningful question about the fitted model is whether we can explain the among-location variations in model parameters, especially the changepoint and the rate of change. To answer this question, we need additional location-specific variables that can be used to distinguish one site from another. Such variables are known as “group-level” predictors in multilevel model terminology [15]. Although we were unable to explain the changes of the changepoint, ϕ, and slope of the right line segment, β, using group-level predictors such as latitude, elevation, ecoregions, and USDA Plant Hardiness Zones, the capability of a hierarchical model to include group-level predictors is an important feature which can be easily incorporated in a causal analysis (Supplemental Fig. 2 available at GitHub.com/StephAnnieNummer/Lilac_HockeyStick_BHM, [15, 31]). Location-specific weather and climate data were not included as variables in the Bayesian hierarchical hockey-stick model because these data would introduce additional noise that we aim to reduce with the hierarchical method, and modeled climatic data can incorporate additional assumptions into the model. We note that lilacs are an introduced species which may explain the lack of geographic pattern in association with latitude, elevation, ecoregion, or USDA harshness zones. With lilacs blooming earlier in the year, a natural question is how this change in lilac first bloom dates translates through trophic levels. Previous research has found instances of trophic mismatch where interdependent populations are responding to the global average temperature at different rates, as well as significant differences between functional groups [4, 21, 22, 27]. For example, Both et al. [4] noted the potential difference in the peak of food availability for birds and the timing of birds breeding season as a result of the differential responses to climate change. Similarly, Parmesan [27] demonstrated contrasting degrees of advancements between butterflies and flowering herbs in response to climate change, which can be problematic because of the mutually dependent relationship between butterflies and flowering herbs in all life-stages. The mismatch between these two populations has the potential to grow further apart or converge depending on when the mismatch started for each population [27].

In our example, we modeled the response of a single species over multiple locations to summarize the impact of climate change on the species. The same model can be used to analyze patterns of change in multiple species at a single location to study the community response. Such an application is ideally suited for predicting potential mismatch of multiple co-dependent species, enhancing our understanding of the impact of climate change on biodiversity due to trophic mismatches.