Effects of multiple slip conditions on hydromagnetic flow of Jeffrey fluid over a deformable porous channel

Abstract

Present study numerical solution on hydromagnetic flow of Jeffrey fluid over a deformable porous channel with slip conditions is studied. The governing partial differential equations are converted to ordinary non-linear differential equations with the assistance of non-dimensional quantities. The governing differential equations are solved by using Runge–Kutta fourth order besides shooting technique with MATLAB package and also the mass flow rate is additionally studied. The influence of governing parameters on the fluid velocity, the solid displacement and also the concentration are shown with the assistance of graphs. The current results are sensible agreement with existing studies under some special cases. We have a tendency to discovered that the fluid velocity, solid displacements are decay for higher values of magnetic parameter and also the opposite nature discovered for the influence of Jeffrey parameter. The impact of slip boundary conditions on the fluid velocity, the temperature and also the concentration also are studied.

1 Introduction

In recent papers the study heat and mass transfer in fluid flows through porous media is the present space of analysis interest because of its intensive applications in engineering, biology and medicine. Magnetohydrodynamics applications are utilized in engineering and industrial areas like energy conversion, research and development for top potency and low emission electric power generation system, MHD acceleration and MHD thrusters, boundary layer control in aerodynamics. The viscous flow through porous media happens in several industrial things and possesses many necessary scientific and engineering applications like flow through packed beds and ion-exchange beds, energy extraction from the geothermal regions, solid filtration from liquids, extracting petroleum and other oils, from underground porous rocks and physiological systems like articular cartilage. Mathematical modeling of deformable porous media have fascinating applications in understanding the blood flow within the tissue region of the blood vessel, synovial fluid flow in erythrocyte deformability. In view of those applications Asghar et al. [1] studied flow and heat transfer analysis during a deformable channel. The magnetohydrodynamics effect is studied in exponentially stretching sheet and asymmetric porous channel were studied by the researchers [2,3,4,5]. In modern technology the researchers are interested to studied deformable porous medium in different channels (vertical, horizontal, inclination channel, and slips) were addressed by the researchers [6,7,8,9,10,11,12,13,14,15,16,17]. Numerical solutions for unsteady flows of a MHD Jeffrey fluid between parallel plates through a porous medium were discovered by Ramesh and Joshi [18]. Effects of thermal radiation and magnetohydrodynamics on Ree–Eyring fluids flows through porous medium with slip boundary conditions were developed by Ramesh and Eytoo [19]. Venkata Satya Narayana et al. [20] studied numerical study of a Jeffrey fluid over a porous stretching sheet with heat source/sink. The researcher analyzed on the nonmaterial’s through heat transfer were studied by Sheikholeslami et al. [21,22,23,24,25,26,27,28,29,30,31] and Rehman et al. [32, 33] developed on heat transfer in the presence of nano-sized particles suspended in a magnetized rotatory flow field and symmetry analysis on thermally magnetized fluid flow regime with heat source/sink. Aman et al. [34] reported on heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Vishnu Ganesh et al. [35] analyzed Riga-plate of $\gamma$ Al₂O₃ water/ethylene glycol with effective Prandtl number impacts. MHD flow of fractional Maxwell fluid in a porous medium with heat transfer and second order slip effect was developed by Aman et al. [36]. The nanofluids over a stretching sheet were examined by Vishnu Ganesh et al. [37,38,39].

Present paper analyzed numerical answer on hydromagnetic flow of Jeffrey fluid over a deformable porous channel with slip conditions. The governing equations are solved numerically with shooting technique. The impact of governing parameters on the fluid velocity, the solid displacement and also the concentrations are shown with the assistance of graphs. The mass flow rate is shown numerically in tabulated type.

2 Mathematical formulation of the problem

Combination of continuous mixture fluid and solid phases are one of the modeled in porous material where the fluid mixture is occupied both fluid and solid simultaneously and it is indicated by $\beta = s,f$.

Every phase in the density of the mixture is $\rho^{\beta } = \rho^{\beta } T\phi^{\beta }$ where $\rho^{\beta } T$ is the intrinsic density and $\phi^{\beta }$ the volume fraction of component $\beta$. For a binary system $\phi^{s} + \phi^{f} = 1$. The interactive force between the constituents are shown as

$$\pi^{f} = - \pi^{s} = K\left( {\upsilon^{s} - \upsilon^{f} } \right) = p\nabla \phi^{s}$$

(1)

where $K$ is the coefficient of drag.

Assumed that the deformation of the solid matrix are small then solid stress can be represented as

$$\sigma^{s} = \lambda tr(e)I + 2\mu e\quad {\text{with}}\quad e = \frac{1}{2}\left( {\nabla u + \nabla u^{T} } \right)$$

(2)

where $\lambda$ and $\mu$ are the Lame constants, $u$ is the solid displacement vector.

For the fluid

$$\sigma^{s} = \mu_{a} \left( {\nabla \vec{\upsilon }^{f} + \left( {\nabla \vec{\upsilon }^{f} } \right)^{T} } \right)$$

(3)

where $\mu_{a}$ is the fluid apparent viscosity in the porous material.

The continuity equation for each phase can be represented with the relation of Jain and Jayaraman [40].

$$\frac{{\partial \phi^{\beta } }}{\partial t} + \nabla \cdot \left( {\phi^{\beta } \upsilon^{\beta } } \right) = 0$$

(4)

where the solid velocity $\upsilon^{s} = \frac{\partial u}{\partial t}$ and $u$ is the solid displacement vector. The over all continuity equation is derived by adding the equations for both phases,

$$\nabla \cdot \left( {\phi^{s} \upsilon^{s} + \phi^{f} \upsilon^{f} } \right) = 0$$

(5)

Both the fluid and the solid phases for the momentum equation are as follows:

$$\rho^{\beta } \left( {\frac{{\partial \upsilon^{\beta } }}{\partial t} + \upsilon^{\beta } \cdot \nabla \upsilon^{\beta } } \right) = \nabla \cdot T^{\beta } + \pi^{\beta }$$

(6)

where $T^{\beta }$ is the stress tensor and $\pi^{\beta }$ is an internal interaction force between the constituents.

The stress tensors constitutive equations for an incompressible Jeffrey fluid are given by following equation

$$\begin{aligned} T^{\beta } & = - \phi^{\beta } pI + \sigma^{\beta } + \bar{S} - \sigma B_{0}^{2} \upsilon \\ \bar{S} & = \frac{{\mu_{a} }}{{1 + \lambda_{1} }}\left( {\dot{\gamma } + \lambda_{2} \ddot{\gamma }} \right) \\ \end{aligned}$$

(7)

The thermal energy and the mass diffusion equation are as follows:

$$\rho^{\beta } \left( {\frac{{\partial T^{\beta } }}{\partial t} + T^{\beta } \cdot \nabla T^{\beta } } \right) = k\nabla^{2} \cdot T^{\beta } + \frac{{\mu_{a} }}{{1 + \lambda_{1} }}\left( {\frac{\partial \upsilon }{\partial y}} \right)^{2} + Q_{0}$$

(8)

$$\left( {\frac{{\partial C^{\beta } }}{\partial t} + C^{\beta } \cdot \nabla C^{\beta } } \right) = D_{B} \nabla^{2} \cdot C^{\beta } - R\left( {C - C_{0} } \right)$$

(9)

3 Geometry flow of the problem

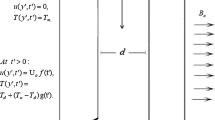
Consider, the steady hydromagnetic flow of Jeffrey fluid over a deformable porous channel with slip conditions. The physical model of the problem is shown in Fig. 1. The fluid flow direction is taken as on the $x$-axis and $y$-axis is perpendicular thereto. The subsequent assumptions square measure thought about to boost the mathematical model:

Fig. 1

Geometry of the problem

• 1. It is assumed that the inclined barring plates are moving with distinct velocities $U_{1}$ and $U_{2}$ respectively.

• 2. The applied transverse magnetic field strength is $B_{0}$ during which the electric field and magnetic Reynolds range are negligible.

• 3. The plates $T_{w} ,T_{0}$ are having distinct temperatures and also the distinct concentrations $C_{w} ,C_{0}$ respectively.

• 4. A pressure gradient $\frac{\partial p}{\partial x}$ is applied producing an axially directed flow. Due to the assumption of an infinite channel there is assumed to be no $x$ dependence in any of the terms except the pressure given by Barry et al. [14].

The governing equations of the momentum, the solid displacement, the temperature and the concentration equations are given by Sreenadh et al. [8, 14, 16, 41]:

$$\frac{{2\mu_{a} }}{{1 + \lambda_{1} }}\frac{{\partial^{2} \upsilon }}{{\partial y^{2} }} - \phi \frac{\partial p}{\partial x} - \sigma B_{0}^{2} \upsilon + \rho g\sin \theta - Kv = 0$$

(10)

$$\mu \frac{{\partial^{2} u}}{{\partial y^{2} }} - (1 - \phi )\frac{\partial p}{\partial x} + \rho g\sin \theta + Kv = 0$$

(11)

$$K_{0} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{2\mu_{a} }}{{1 + \lambda_{1} }}\left( {\frac{\partial \upsilon }{\partial y}} \right)^{2} + Q_{0} = 0$$

(12)

$$D_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} - R\left( {C - C_{0} } \right) = 0$$

(13)

The governing boundary conditions are given by Krishna Murthy et al. [3, 5]

$$\begin{aligned} \upsilon & = U_{1} + L_{1} \frac{\partial \upsilon }{\partial y},\;\;u = 0,\;\;T = T_{0} + L_{2} \frac{\partial T}{\partial y},\;\;C = C_{0} + L_{3} \frac{\partial C}{\partial y}\;at\;y = - h \\ \upsilon & = U_{2} ,\;\;u = 0,\;\;T = T_{1} ,\;\;C = C_{1} \;\;at\;\;y = h \\ \end{aligned}$$

(14)

Now introducing the non-dimensional quantities are as follows:

$$\begin{aligned} Fr & = \frac{U}{gh},\;\;U_{{_{1} }}^{*} = \frac{{U_{1} }}{U},\;\;U_{{_{2} }}^{*} = \frac{{U_{2} }}{U},\;\;y^{*} = \frac{y}{h},\;\;\upsilon^{*} = \frac{\upsilon }{U},\;\;x^{*} = \frac{x}{h},\;\;\gamma = \frac{{Rh^{2} }}{{D_{B} }} \\ T^{*} & = \frac{{T - T_{0} }}{{T_{w} - T_{0} }},\;\;C^{*} = \frac{{C - C_{0} }}{{C_{w} - C_{0} }}p^{*} = \frac{hp}{{2\mu_{a} U}},\;\;u^{*} = \frac{u\mu }{{2\mu_{a} U}},\;\;\frac{dp}{dx} = P,\;\;\delta = \frac{{Kh^{2} }}{{2\mu_{a} }} \\ Re & = \frac{\rho Uh}{{2\mu_{a} }},\;\;\beta = Q_{0} \left( {\frac{{h^{2} }}{{K_{0} \left( {T_{w} - T_{0} } \right)}}} \right),\;\;Br = \frac{{2\mu_{a} U^{2} }}{{K_{0} \left( {T_{w} - T_{0} } \right)}},\;\;M^{2} = \frac{{\sigma B_{0}^{2} h^{2} }}{\mu } \\ \end{aligned}$$

(15)

Using Eq. (15) in Eqs. (10)–(14) and after neglecting the asterisks (*) takes the following equations are:

$$\frac{1}{{1 + \lambda_{1} }}\frac{{d^{2} \upsilon }}{{dy^{2} }} - \phi P + \frac{Re}{Fr}\sin \theta - \left( {\delta + M^{2} } \right)\upsilon = 0$$

(16)

$$\frac{{d^{2} u}}{{dy^{2} }} - (1 - \phi )P + \frac{Re}{Fr}\sin \theta + \delta \upsilon = 0$$

(17)

$$\frac{{d^{2} \theta }}{{dy^{2} }} + \frac{Br}{{1 + \lambda_{1} }}\left( {\frac{d\upsilon }{dy}} \right)^{2} + \beta = 0$$

(18)

$$\frac{{d^{2} \phi }}{{dy^{2} }} - \gamma \phi = 0$$

(19)

The boundary conditions are

$$\begin{aligned} \upsilon & = U_{1} + \alpha_{1} \frac{d\upsilon }{dy},\;u = 0,\;\theta = \alpha_{2} \frac{d\theta }{dy},\;\phi = \alpha_{3} \frac{d\phi }{dy}\;at\;y = - 1 \\ \upsilon & = U_{2} ,\;u = 0,\;\theta = 1,\;\phi = 1\;at\;y = 1 \\ \end{aligned}$$

(20)

4 Mass flow rate

The non-dimensional mass flow rate $M_{1}$ per unit width of the channel as follows:

$$M_{1} = \int\limits_{0}^{1} {\upsilon dy}$$

(21)

We are interest to finding the Shear stress, the Nusselt number and the Sherwood number as follows:

$$\tau = \frac{1}{{1 + \lambda_{1} }}\left( {\frac{d\upsilon }{dy}} \right)_{at\;y = - 1} ,\quad Nu = - \left( {\frac{d\theta }{dy}} \right)_{at\;y = - 1} ,\quad Sh = - \left( {\frac{d\phi }{dy}} \right)_{at\;y = - 1}$$

(22)

5 Numerical method for the solution

The converted governing dimensionless equations in (16)–(19) with the corresponding boundary conditions (20) are solved using the Runge–Kutta fourth order methodology together with shooting technique. The boundary value problem is initially converted into associate degree an initial value problem and then solved it numerically by taking step size of $h = 0.01$ with 201 iterations then we get $y = 1$ it’s represent that the terminal value within the domain. The solutions are obtained with the convergence criterion of $10^{ - 8}$ in all cases. The accuracy of this numerical simulation results are valid with the previous result of Gopi Krishna et al. [41] and Nield et al. [42] see Table 1 are found sensible agreement with their results. During this methodology, the transformed non-linear differential equations to a primary order differential equation, by mistreatment the subsequent method:

$$\begin{aligned} f(1) & = \upsilon ,\;f(2) = \upsilon^{\prime } ,\;f(3) = u,\;f(4) = u^{\prime } ,\;f(4) = \theta ,\;f(5) = \theta^{\prime } \\ f(6) & = \phi ,\;f(7) = \phi^{\prime } \\ \end{aligned}$$

(23)

$$\begin{aligned} \upsilon^{\prime \prime } & = \left[ {\phi P - \frac{Re}{Fr}\sin \theta + \left( {\delta + M^{2} } \right)f(1)} \right]\left( {1 + \lambda_{1} } \right) \\ u^{\prime \prime } & = \left[ {(1 - \phi )P - \frac{Re}{Fr}\sin \theta - \delta f(1)} \right] \\ \theta^{\prime \prime } & = - \frac{Br}{{1 + \lambda_{1} }}f(2)^{2} - \beta \\ \phi^{\prime \prime } & = \gamma f(7) \\ \end{aligned}$$

(24)

with the boundary conditions are as follows:

$$\begin{aligned} f(1) & = U_{1} + \alpha_{1} f(2),\;f(3) = 0,\;f(5) = \alpha_{2} f(6),\;f(7) = \alpha_{3} f(8)\;at\;y = - 1 \\ f(1) & = U_{2} ,\;f(3) = 0,\;f(5) = 1,\;f(7) = 1\;at\;y = 1 \\ \end{aligned}$$

(25)

6 Results and discussion

In this paper Hydro magnetic flow of Jeffrey fluid over a deformable porous channel with slip conditions is studied. The solid displacement, the fluid velocity, the temperature and therefore the concentration are solved by making use with shooting technique. The impacts of governing parameters on the solid displacement, the fluid velocity, the temperature and therefore the concentration are shown with the assistance of the graphs whereas the mass flow rate is found numerically.

It is clearly see from Fig. 2a the results are good agreement with Gopi Krishna et al. [41] when the absence of magnetic parameter, Jeffrey parameter and the velocity slip parameter.

Fig. 2

a The impact of $\lambda_{1}$ on the fluid velocity $\upsilon (y)$, b the impact of $\delta$ on the fluid velocity $\upsilon (y)$

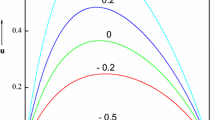
The result of viscous drag $\delta$ on the fluid velocity $\upsilon (y)$ and also the solid displacement $u(y)$ is shown in Figs. 2b and 3. We have seen that the fluid velocity reduces with enhancing viscous drag and also the opposite behavior on the solid displacement. These causes the drag forces are acquiring in reverse direction to the target relative motion which might be perpetually opposes the motion. Thus the fluid velocity decays for higher values of drag forces. The impact of angle of inclination $\theta$ on the fluid velocity $\upsilon (y)$ and also the solid displacement $u(y)$ are shown in Figs. 4 and 5. We have a tendency to detect the each fluid flow and also the solid displacement is decrease for higher values of angle of inclination. From Figs. 6, 7, 8 and 9 we have a tendency to detected that the fluid velocity $\upsilon (y)$ and also the solid displacement $u(y)$ are enhance for higher values of moving velocities $U_{1}$ and $U_{2}$. The influence of volume fraction of the fluid $\phi$ on the fluid velocity $\upsilon (y)$ and therefore the solid displacement $u(y)$ are portrayed in Figs. 10 and 11. We tend to ascertained that the fluid velocity increases with increasing volume fraction of the fluid and therefore the opposite nature ascertained within the solid displacement. The variation of magnetic parameter $M$ on the fluid velocity $\upsilon (y)$ and therefore the solid displacement $u(y)$ are elucidated in Figs. 12 and 13. We tend to reveals that each the fluid velocity and therefore the solid displacement are decrease for enhance magnetic parameter. This decreasing result within the fluid velocity and therefore the solid displacement are unit a longtime result as a result of the flux acts within the transversal direction to the flow and the magnetic attraction resists the flow. Figures 14 and 15 are represents the influence of Jeffrey parameter $\lambda_{1}$ on the fluid velocity $\upsilon (y)$ and the therefore solid displacement $u(y)$. We tend to found that each the fluid velocity and therefore the solid displacement are enhancing for higher values of Jeffrey parameter. The impacts of the fluid velocity slip parameter $\alpha_{1}$, the temperature slip parameter $\alpha_{2}$ and the concentration slip parameter $\alpha_{3}$ on the fluid velocity $\upsilon (y)$, the temperature $\theta (y)$ and the concentration $\phi (y)$ are portrayed in Figs. 16, 17 and 18. We reveal that the fluid velocity reduces with increasing the fluid velocity slip parameter and also the opposite behavior ascertained within the temperature and also the concentration for higher values of the temperature slip parameter and also the concentration slip parameter. The influence of Brinkman number $Br$ variety on the temperature $\theta (y)$ is delineated in Fig. 19. We’ve got seen that the temperature increases with increasing Brinkman variety. It is the numerous parameter in unchangeability. For Higher numerical values of $Br$ we tend to detected that a lower contribution in thermal physical phenomenon generated via viscous dissipation and larger elevation in temperature. So the temperature increases with increasing Brinkman range. The impact of heat source parameter $\beta$ on the temperature distribution $\theta (y)$ is shown in Fig. 20. We tend to detected that the temperature enhances with enhancing heat source parameter. The variation of chemical reaction parameter $\gamma$ on the concentration $\phi (y)$ is displayed in Fig. 21. We tend to examined that the concentration reduces for higher values of chemical reaction parameter. The impact of magnetic parameter $M$ on the shear stress at the lower wall $\tau ( - 1)$ is displayed in Fig. 22. We reveal that the shear stress decays for higher values of magnetic parameter. From Fig. 23 depicts that the effect of Jeffrey parameter $\lambda_{1}$ on the Nusselt number $- \theta^{\prime } ( - 1)$. We have seen that it is enhances with enhancing Jeffrey parameter. The impact of chemical reaction $\gamma$ on the Sherwood number is depicted in Fig. 24. We’ve seen that the Sherwood number enhance with increasing chemical reaction.

Fig. 3

The impact of $\delta$ on the solid displacement of $u(y)$

Fig. 4

The impact of $\theta$ on the fluid velocity $\upsilon (y)$

Fig. 5

The impact of $\theta$ on the solid displacement $u(y)$

Fig. 6

The impact of $U_{1}$ on the fluid velocity $\upsilon (y)$

Fig. 7

The impact of $U_{1}$ on the solid displacement $u(y)$

Fig. 8

The impact of $U_{2}$ on the fluid velocity $\upsilon (y)$

Fig. 9

The impact of $U_{2}$ on the solid displacement $u(y)$

Fig. 10

The impact of $\phi$ on the fluid velocity $\upsilon (y)$

Fig. 11

The impact of $\phi$ on the solid displacement $u(y)$

Fig. 12

The impact of $M$ on the fluid velocity $\upsilon (y)$

Fig. 13

The impact of $M$ on the solid displacement $u(y)$

Fig. 14

The impact of $\lambda_{1}$ on the fluid velocity $\upsilon (y)$

Fig. 15

The impact of $\lambda_{1}$ on the solid displacement $u(y)$

Fig. 16

The impact of $\alpha_{1}$ on the fluid velocity $\upsilon (y)$

Fig. 17

The impact of $\alpha_{2}$ on the temperature $\theta (y)$

Fig. 18

The impact of $\alpha_{3}$ on the concentration $\phi (y)$

Fig. 19

The impact of $Br$ on the temperature $\theta (y)$

Fig. 20

The impact of $\beta$ on the temperature $\theta (y)$

Fig. 21

The impact of $\gamma$ on the concentration $\phi (y)$

Fig. 22

The impact of $M$ on the Shear stress at the lower wall $\tau ( - 1)$

Fig. 23

The impact of $\lambda_{1}$ on the Nusselt number at the lower wall $- \theta^{\prime } ( - 1)$

Fig. 24

The impact of $\gamma$ on the Sherwood number at the lower wall $- \phi^{\prime } ( - 1)$

The numerical values of the mass flow rate $M_{1}$ with deformable porous medium and undeformable porous medium are shown in Table 1. We noticed that the volume flow rate $M_{1}$ with deformable porous medium reduces for higher worth of drag coefficient $\delta$ for fixed value of $\phi = 0.6$. The constant nature is noticed that within the case of mass flow rate $M_{1}$ with undeformable porous medium Nield et al. [42] for higher values of Darcy number $Da$. The Present results are sensible agreement with existing studies Nield et al. [42] once $M = 0,\;\lambda_{1} = 0,\;\theta = 0,\;\alpha_{1} = \alpha_{2} = \alpha_{3} = 0$ and drag parameter $\delta$ in deformable porous medium is adequate to the Darcy number $Da$ porous medium in a channel for the case of $\phi = 1$.

Table 1 Numerical values of mass flow rate $M_{1}$ with distinct values of $Da$ and $\delta$

7 Conclusions

In this paper we have to tendency to study Hydro magnetic flow of Jeffrey fluid over a deformable porous channel with slip conditions. The non-linear coupled differential equations are solved using shooting technique. The influences of Jeffrey parameter, magnetic parameter, Brinkmann number, viscous drag, volume fraction of the fluid, angle of inclination, heat source parameter, Upper and lower plate moving velocities, chemical reaction parameter, the fluid velocity slip parameter, the temperature and also the concentration slip parameters on the fluid velocity, the solid displacement and the temperature are shown in diagrammatically. The mass flow rate is calculated numerically and displayed in tabular form. The conclusions are as follows

• The fluid velocity and the solid displacement are enhancing with the effect of Jeffrey parameter, angle of inclination, lower and upper plate moving velocities.

• The temperature enhances with an impact of Brinkmann number and heat source parameters.

• The fluid velocity and the solid displacement are decreases with the influence of magnetic parameter.

• The variation of viscous drag the velocity reduces and the opposite nature observed in sold displacement. The fluid velocity and the solid displacement are having opposite behavior with the influence of volume fraction coefficient.

• An increasing the temperature slip parameter and the concentration slip parameter causes the temperature and the concentration are increase, The fluid velocity reduces with the impact of velocity slip parameter,

• The influence of chemical reaction parameter on the concentration displayed a decreasing nature.

• The shear stress suppress at the lower wall once increasing numerical values of magnetic parameter, the Nusselt number decays once increasing Jeffrey parameter and the Sherwood number enhances with enhancing chemical reaction.

• The present results are good agreement when compared with Gopi Krishna et al. [41] and Nield et al. [42] under some special cases.