Abstract
Improvement in some aspect of ecology and financial mathematics is strongly dependent on the analytical solution of Bagley-Torvik equations. The aim of this manuscript is to find the analytical solution of Bagley-Torvik equations which belongs to a class of fractional differential equation by the use of Sumudu transformation method (STM). Here the fractional derivatives are well-defined in Caputo sense. First, some fundamental properties of STM are given, and then STM is applied to the Bagley-Torvik equation which gives an exact solution. The proposed method is an easy, highly efficient and robust method for finding the exact solution.
Similar content being viewed by others
1 Introduction
In current years, fractional calculus (FC) has found to be important in various fields viz fluid dynamics, ecology, financial mathematics [1,2,3,4,5,6]. It is sometimes difficult to obtain the analytical solution of the fractional differential equations (FDEs). Various important research on FC has been deliberated in the past years, and a lot of books have been written by various authors namely Miller and Ross [7], Oldham and Spanier [8], Podlubny [9]. General ideas about FC are introduced in these books which may help the readers to understand the basic concepts of FC. Recently some analytical and numerical techniques have been developed for the solution of physical problems viz. homotopy perturbation method by Wu and He [10], modified homotopy perturbation method by Jena and Chakraverty [11], Adomian decomposition method by Momani and Odibat [12] and Yavuz and Ozdemir [13], and modified decomposition method by Edeki et al. [14].
In the above regard, STM has been found to be a novel method to handle FDEs. The STM was first introduced by Watugala in 1993. This method was implemented to solve various types of engineering control problems by Watugala [15, 16] too. Later, this method was extended to solve two-dimensional engineering problem by Watugala [17]. The significant applications to partial differential equations and inversion formulae were established in two papers by Weerakoon [18, 19] in 1994 and 1998. The Sumudu transform was also first defined by Weerakoon against Deakin’s definition who claimed that there is no difference between the Sumudu and the Laplace and who reminded Weerakoon that the Sumudu transform is really the S-multiplied transform disguised in Deakin [20] and Weerakoon [21]. The solutions of integral equations and discrete dynamical systems of convolution type using STM were later achieved by Asiru [22,23,24]. The Sumudu transform was also used to solve many ordinary differential equations with integer order and although Belgacem’s reasonable advantages for implementing to fractional differential equations commenced in 2008 with various teams of researchers in Katatbeh and Belgacem [25]. It is worth mentioning that novel STM has not been used in solving the Bagley-Torvik equation. So to the best of the present authors’ knowledge, this is the first time that STM has been implemented for solving fractional order Bagley-Torvik equation.
In this paper, the following type of Bagley-Torvik equation is considered
where m, c, k, f(x) and u(x) denote the mass, damping, stiffness coefficients, external force, and displacement function, respectively. \( \frac{{d^{\alpha } u}}{{dx^{\alpha } }} \) is the FD of order \( \alpha \in (0,2) \). Here \( \delta_{0} \) and \( \delta_{1} \) are real constants.
The rest of the manuscript are arranged as follows: some essential definitions related to fractional calculus are included in Sect. 2. Some basic features and theorems of STM are presented in Sect. 3. In Sect. 4, STM is applied to Bagley-Torvik Equation. Finally, a conclusion is illustrated in Sect. 6.
2 Basic features of fractional calculus
Definition 2.1
The operator \( D^{\alpha } \) of order \( \alpha \) in Abel–Riemann (A–R) sense is defined by Podlubny [9] as
where \( m \in Z^{ + } , \)\( \alpha \in R^{ + } \) and
Definition 2.2
The A–R fractional order integration operator \( J^{\alpha } \) is described as
following Podlubny [9] we may have
Definition 2.3
The operator \( D^{\alpha } \) of order \( \alpha \) in the Caputo sense is defined in Podlubny [9] and Chakraverty et al. [26] as
Definition 2.4
Podlubny [9]
-
(a)
$$ D_{t}^{\alpha } J_{t}^{\alpha } f\left( t \right) = f\left( t \right) $$(8)
-
(b)
$$ J_{t}^{\alpha } D_{t}^{\alpha } f\left( t \right) = f\left( t \right) - \sum\limits_{k = 0}^{m} {f^{\left( k \right)} \left( {0^{ + } } \right)} \frac{{t^{k} }}{k!},\;{\text{for}}\;t > 0\;{\text{and}}\;m - 1 < \alpha \le m,\;m \in N. $$
3 Basic properties of STM
Definition 3.1
If \( F\left( u \right) \) is the Sumudu transform (ST) of \( y\left( t \right) \), then the ST of \( y\left( t \right) \) for all real number \( t \ge 0, \) is defined in Weerakoon [18] as
Theorem 1
If \( F\left( u \right) \) is the ST of \( y\left( t \right) \), then the ST of \( n^{th} \) order derivative is defined in Belgacem et al. [27] as follows
By using Theorem 1, the ST of \( \frac{dy\left( t \right)}{dt} \) and \( \frac{{d^{2} y\left( t \right)}}{{dt^{2} }} \) are given by
Theorem 2
The ST of Caputo fractional derivative is well-defined in Chaurasia and Singh [28] as
4 STM implementation to Bagley-Torvik equations
In this section, STM is implemented to Bagley-Torvik equations of fractional order in the following examples.
Example 1
Let us take following Bagley-Torvik equation given by Pedas and Tamme [29]
First, by taking ST of both sides of Eq. (14), we get
which yields
Using initial condition to Eq. (15), we get
Applying inverse ST to Eq. (16) and the table presented by Belgacem and Karaballi in [30], we have
This is the analytical solution of Eq. (14).
Example 2
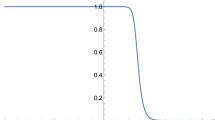
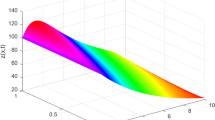
Let us now solve the following Bagley-Torvik equation given in Parisa and Yadollah [31] and (Figs. 1, 2) Mohammadi and Mohyud-Din [32] as
An inflexible plate of mass m dipped into a Newtonian fluid presented by Gülsu et al. [33]
Applying ST on both sides of Eq. (18) with the initial condition, we get
Taking inverse ST of Eq. (19) and from the table in Belgacem and Karaballi [30], we get
This is the analytical result of Eq. (18).
Example 3
Further, consider the following Bagley-Torvik equation in Ford and Connolly [34]
First, apply STM on both sides of Eq. (21) and initial condition to get
Applying inverse ST to Eq. (22) and using the table in Belgacem and Karaballi [30], we find the analytical solution of Eq. (22) as follows
Example 4
Finally, let us take the Bagley-Torvik equation in Ford and Connolly [34]
Taking ST on both sides of Eq. (24) and initial condition, the subsequent equation is obtained as
Applying inverse ST to Eq. (25) and from the table in Belgacem and Karaballi [30], we have
which is the exact solution of Eq. (24).
5 Conclusion
In this paper, STM is successfully applied to solve Bagley-Torvik equations. Four examples are solved by STM which show that it is a very useful and highly effective technique in term of yielding an analytical solution. Due to its properties, it is mostly used for solving a different kind of linear and nonlinear fractional differential equation for finding the exact solution.
References
Deng R, Davies P, Bajaj AK (2004) A case study on the use of fractional derivatives: the low frequency viscoelastic uni-directional behavior of polyurethane foam. Nonlinear Dyn 38:247–265
Rossikhin YA, Shitikova MV (2004) Analysis of the viscoelastic rod dynamics via models involving fractional derivatives or operators of two different orders. Shock Vib Dig 36(1):3–26
Agrawal OP (2004) Analytical solution for stochastic response of a fractionally damped beam. ASME J Vib Acoust 126(4):561–566
Jena RM, Chakraverty S (2019) A new iterative method based solution for fractional Black-Scholes option pricing equations (BSOPE). SN Appl Sci 1(1):95
Shah NA, Hajizadeh A, Zeb M, Ahmad S, Mahsud Y, Animasaun IL (2018) Effect of magnetic field on double convection flow of viscous fluid over a moving vertical plate with constant temperature and general concentration by using new trend of fractional derivative. Open J Math Sci 2:253–265
Shah NA, Elnaqeeb T, Animasaun IL, Mahsud Y (2018) Insight into the natural convection flow through a vertical cylinder using caputo time-fractional derivatives. Int J Appl Comput Math 4:80–99
Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York
Oldham KB, Spanier J (1974) The fractional calculus. Academic Press, New York
Podlubny I (1999) Fractional differential equations. Academic Press, New York
Wu Y, He JH (2018) Homotopy perturbation method for nonlinear oscillators with coordinate dependent mass. Results Phys 10:270–271
Jena RM, Chakraverty S (2019) Solving time-fractional Navier-Stokes equations using homotopy perturbation Elzaki transform. SN Appl Sci 1(1):16
Momani S, Odibat Z (2006) Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method. Appl Math Comput 177:488–494
Yavuz M, Ozdemir N (2018) A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J Math 6(1):102–109
Edeki SO, Motsepa T, Khalique CM, Akinlabi GO (2018) The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method. Open Phys 16:780–785
Watugala GK (1993) Sumudu transform: a new integral transform to solve differential equations and control engineering problems. Int J Math Educ Sci Technol 24(1):35–43
Watugala GK (1998) Sumudu transform—a new integral transform to solve differential equations and control engineering problems. Math Eng Ind 6(4):319–329
Watugala GK (2002) The Sumudu transform for functions of two variables. Math Eng Ind 8(4):293–302
Weerakoon S (1994) Application of Sumudu transform to partial differential equations. Int J Math Educ Sci Technol 25(2):277–283
Weerakoon S (1998) Complex inversion formula for Sumudu transform. Int J Math Educ Sci Technol 29(4):618–621
Deakin MAB (1997) The Sumudu transform” and the Laplace transform. Int J Math Educ Sci Technol 28(1):159–160
Weerakoon S (1997) The Sumudu transform and the Laplace transform—reply. Int J Math Educ Sci Technol 28(1):160
Asiru MA (2001) Sumudu transform and the solution of integral equations of convolution type. Int J Math Educ Sci Technol 32(6):906–910
Asiru MA (2002) Further properties of the Sumudu transform and its applications. Int J Math Educ Sci Technol 33(3):441–449
Asiru MA (2003) Application of the Sumudu transform to discrete dynamical systems. Int J Math Educ Sci Technol 34(6):944–949
Katatbeh QD, Belgacem FBM (2011) Applications of the Sumudu transform to fractional differential equations. Nonlinear Stud 18(1):99–112
Chakraverty S, Tapaswini S, Behera D (2016) Fuzzy arbitrary order system: fuzzy fractional differential equations and applications. Wiley, New York
Belgacem FBM, Karaballi AA, Kalla SL (2003) Analytical investigations of the Sumudu transform and applications to integral production equations. Math Probl Eng 2003(3):103–118
Chaurasia VBL, Singh J (2010) Application of Sumudu transform in Schödinger equation occurring in quantum mechanics. Appl Math Sci 4(57):2843–2850
Pedas A, Tamme E (2011) On the convergence of spline collocation methods for solving fractional differential equations. J Comput Appl Math 235:3502–3514
Belgacem FBM, Karaballi AA (2006) Sumudu transform fundamental properties investigations and applications. J Appl Math Stoch Anal 2006:23
Parisa R, Yadollah O (2018) Application of Müntz-Legendre polynomials for solving the Bagley-Torvik equation in a large interval. seMA 75:517–533
Mohammadi F, Mohyud-Din ST (2016) A fractional-order Legendre collocation method for solving the Bagley-Torvik equations. Adv Differ Equ 2016:269–283
Gülsu M, Öztürk Y, Anapali A (2017) Numerical solution the fractional Bagley-Torvik equation arising in fluid mechanics. Int J Comput Math 94(1):173–184
Ford NJ, Connolly JA (2009) Systems-based decomposition schemes for the approximate solution of multi-term fractional differential equations. J Comput Appl Math 229:382–391
Acknowledgements
The first author would like to thank Department of Science and Technology, Government of India for giving INSPIRE fellowship (IF170207) to carry out the present work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jena, R.M., Chakraverty, S. Analytical solution of Bagley-Torvik equations using Sumudu transformation method. SN Appl. Sci. 1, 246 (2019). https://doi.org/10.1007/s42452-019-0259-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-019-0259-0