Abstract
Proper management of municipal solid waste is one of the prime matters of concern for metropolitan cities. To be able to successfully manage the solid waste generated, we need to plan in advance. A very essential pre-requirement for an efficient solid waste management is an accurate prediction of the garbage generation. Accurate forecasting of the quantity of MSW generation will enable us to design and operate an effective waste collection system. The main objective of this paper is to compare different models of artificial intelligence, viz. artificial neural network (ANN), adaptive neuro-fuzzy inference system (ANFIS), discrete wavelet theory–artificial neural network (DWT-ANN), discrete wavelet theory–adaptive neuro-fuzzy inference system (DWT-ANFIS), genetic algorithm–artificial neural network (GA-ANN) and genetic algorithm–adaptive neuro-fuzzy inference system (GA-ANFIS) to examine and evaluate their capability in forecasting the amount of garbage being generated. A case example of the city of New Delhi, India, has been used for better understanding of different models. Root mean square error (RMSE), coefficient of determination (R2) and index of agreement (IA) values for every model were calculated, and the models were compared on the basis of it. The hybrid model of genetic algorithm and artificial neural network was found to have the lowest RMSE, the highest IA value and the highest R2 values, and hence is the most accurate of the above six models.
Similar content being viewed by others
1 Introduction and literature review
Error-free forecasting of the quantity of municipal solid waste (MSW) production is the prime requirement for the design as well as operation of an efficient system of waste management. Imprecise forecasting may be the cause of widespread inefficiencies in the waste management infrastructure such as excessive or insufficient disposal infrastructure (collection, landfill, incinerators or recycling units) [5]. The necessity of a correct forecast is even more in the case of a metropolitan city like New Delhi, India, so that a proper measure can be planned in advance. These measures not only include development as well as improvement in existing facilities but also sensitize the people so as to promote reduction, reutilization as well as recycling of the solid waste generated. If the waste generated cannot be managed properly, it may lead to devastating environmental as well as health hazards [9]. Because of the significant impact of waste management on the ecosystem, waste management systems having less universal and zonal environmental impacts need to be developed [17]. There are different methods of predicting solid waste generation which can be broadly classified into five main groups: descriptive statistical models, regression analysis, material flow method, time series analysis and artificial intelligence methods [1].
According to Navarro-Esbrı´ et al. [19], analysis of garbage generation which is dynamic in nature could be accomplished with the help of data in the form of a time series, containing the quantity of garbage being produced. This is because such data are dynamic in nature and provide us with a means to overcome the dearth of data regarding other parameters that may influence waste production [6]. As per Beigl et al. [4], quantity of waste generated cannot be determined directly at an individual level due to the presence of several parallel disposal channels (civic amenity sites for green waste, public kerbside collection, bulky waste, etc.). According to Rimaityte et al. [22], time series method is not dependent on other estimated economic or social parameters and hence has an advantage over the techniques based on regression as the analysis of the economic or the social parameters may also be inaccurate. Another advantage of time series analysis is the capability of forecasting seasonal variations in MSW generation. According to Kannangara et al. [13], artificial intelligence-based models have better prediction abilities than other regression-based models. Hence, in this study time series analysis using different artificial intelligence techniques has been done as these methods have the ability to cope with the historical data which are of nonlinear nature.
The models evaluated in this paper are: artificial neural network; discrete wavelet-based ANN; genetic algorithm optimized ANN; adaptive neuro-fuzzy inference system (ANFIS); discrete wavelet-based ANFIS; and genetic algorithm optimized ANFIS. Jalili et al. [11] have used ANN to forecast the quantity of waste being produced in the city of Mashhad for different seasons with the help of time series data of waste generation. Singh et al. [23] have used ANN for time series forecasting of waste generation for the city of Faridabad. Similarly ANN has been used by Sodanil et al. [26] for forecasting waste generation in the city of Bangkok. However, with a large and noisy data set the results of ANN may suffer. Hence, the data may need to be pre-processed by the wavelet method. Also, ANN may get stuck in a local minimum; hence, a hybrid model with GA has also been used in this study so that global minima can be obtained. Abbasi et al. [1] have used ANFIS to predict waste generation in the city of Logan, Australia, using time series data and have compared the model with SVM (support vector machine) and KNN (K nearest-neighbour) models. Noori et al. [20] have used support vector machine along with principal component analysis to model the waste generation in the city of Mashhad using weekly time series data. Fuzzy logic has been used to forecast solid waste for the Canary archipelago by Charles et al. [9]. However, not much work was found with hybrid ANFIS models. Hence, the performance of hybrid ANFIS models in waste prediction was also evaluated in this study. The time series data used were taken from Kumar [15]. The data used contain the yearly MSW generated in the city of New Delhi, India. The data were used with different models, and the different models were evaluated by calculating the RMSE and the IA values.
2 Artificial intelligence model overview
Artificial intelligence (AI) models have been successively used to forecast time series data in different field of studies such as hydrology [2, 18, 19, 27, 28], supply chain demand forecasting [10, 24], electricity price and load forecasting [16, 21], flood forecasting [14]. In the upcoming section, a brief description of the models that have been used in this study has been given. Time series data of waste generated in New Delhi from the period of 1993–2011 were used in this study, and it was assumed that the time series data contain all the patterns associated with waste generation.
2.1 Artificial neural network (ANN)
ANN derives its roots from the biological nervous system that consists of interconnected operational units referred to as neurons [3, 8]. ANN is frequently used due to its capability to inspect patterns in data sets [25]. A neural network learns on the basis of input provided and the output generated. The primary layer of an ANN consists of input neurons which transfer information on to the second layer (hidden layer), which then transfers the processed information to the output neurons of the third layer. The number of neurons in the hidden layer is selected by trial and error method.
ANN is trained using a gradient descent back-propagation algorithm. Any modification in input data is processed using connecting weights; it generates sum of modified value of “x”. It is then further modified by sigmoidal transfer function “f”. In the training phase, predicted output (Opi) and desired output (Dpi) are compared which forms the basis for mean square error (Ep). The last step includes back-propagation from output to input with further modification in weights, till the error minimizes and reaches its limiting value.
2.2 Adaptive neuro-fuzzy inference system
For this study, we have used the Sugeno-type fuzzy inference system. In this type of FIS (fuzzy inference system), the output membership function is either constant or linear. ANFIS incorporates the techniques followed in both ANN and fuzzy inference system [12]. For a FIS with two inputs a and b and one output o, rule base may look like
-
Rule 1 If a is U1 and b is V1, F1 = s1a + r1b + t1
-
Rule 2 If a is U2 and b is V2, F2 = s2a + r2b + t2
These rules represent the fuzzy inference rules. Here U1, U2, V1 and V2 are membership functions, and a and b are supplied parameters (inputs) to the system, with F1 and F2 being outputs acquired from the system.
The nodes present in the different layers perform the following functions:
Layer 1 nodes are the input nodes. Each node here establishes the degree of membership of the inputs on the basis of the suitable fuzzy set or membership function. The output from the node can be defined as:
Layer 2 has the rule nodes. These nodes output the firing strength of the rule by performing cross multiplication of all the incoming signals:
Layer 3 has the averaging nodes. The nodes of this layer output the normalized firing strength of each rule.
Layer 4 contains the consequent nodes. Nodes of this layer perform the computation of the contribution of the ith rule towards the output of the model.
\({\overline{W}}_{i}\) is the result of the third layer and si, ri and ti are the consequent parameters.
Layer 5 is constituted by the output node that performs the summation of all the input signals and computes the overall output,
2.3 Discrete wavelet theory
In wavelet analysis, an input signal is disintegrated into its constituent parts. In Fourier analysis, when a signal is transformed from time domain to frequency-based sinusoidal constituents, the time information of breakdown points, local trends, self-similarity and discontinuities gets lost [26]. In wavelet transform, the signal is decomposed into “wavelets” that are variations in the “mother wavelet”
here α is called scaling parameter, α > 0 and β is known as translation parameter, and t is finite. Ψ is the mother wavelet. The translation and scaling of the mother wavelet allow localization in time and frequency domain, respectively. In DWT, scaling and the translation parameters are dyadic (powers of two) in nature. For DWT, scale α = 2m and translation β = 2mn. In DWT, a signal is passed from two filters and one detail component and one approximation component is obtained. The low-frequency, high-scale components are known as approximations, while the high-frequency, low-scale components of the signal are known as details. Usually the most essential constituent of the signal is approximation as it contains the background information of the signal [2]. This breakdown is continued to reach the desired resolution level.
2.4 Genetic algorithm (GA)
GA is categorized under evolutionary algorithms, which is taken from the Darwin’s theory of evolution. Initially genetic algorithm contains a set of solutions (represented by chromosomes) called population [7]. Solutions from a population are selected which is processed to form a new population. Schematic generation of new population is motivated by a hope that the new population will perform better than the old one. Solutions selected to form new solutions (offspring) are selected by the measure of their fitness—the more suitable they are, the more capable they will be in passing their attributes to the next generation. It is repeated until a pre-defined condition (for example, number of populations or improvement in the best solution) is satisfied.
2.5 Data set
Data in this study were collected from two resources, namely primary and secondary. Secondary data were collected from governmental, semi-governmental and private publications, whereas primary data were recorded from the field survey. Data required and published work related to municipal solid waste management were collected from Municipal Corporation of Delhi (MCD), Central Pollution Control Board (CPCB), New Delhi Municipal Council (NDMC), Delhi Cantonment Board (DCB) and various departments of Government of National Capital Territory of Delhi (GNCTD). These data consist of yearly waste generation from the period of 1993–2011. Data to be fed into the system were formed by applying adjacent windowing technique on the time series data mentioned here, and intervals of windows are taken to be 2 and 4.
2.6 Description of models used
2.6.1 Pure ANN
For the analysis done in this paper, we have used a three-layered neural network containing an input layer, a hidden layer and an output layer. Different combinations with different number of delays (input neurons) and different number of hidden nodes were used to form a number of models.
-
No. of input neurons = 2, 4
-
No. of hidden layer neurons = 5, 10
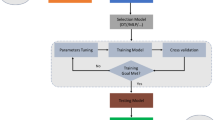
The network was trained with Levenberg–Marquardt back-propagation optimization method. Structure of the network is shown in Fig. 1. The activation function used in the hidden layer is tan-sigmoid, while the one used in the output layer is pure and linear. The model has been created to forecast the next one value, so the number of output nodes is 1. The accuracy of modelling of the different models in terms of RMSE and IA is given in Tables 1 and 2, respectively (Figs. 2, 3, 4).
2.6.2 DWT-ANN
In this hybrid model, discrete wavelet transformation is used to pre-process the input data to improve the forecast efficiency. Breakdown of input signal into simpler constituents is done with the help of DWT decomposition; this makes it easier for ANN to analyse the data. Schematic for this model is given in Fig. 5. First the initial time series signal is broken down into its constituent high- and low-frequency components (detail and approximation) up to the required resolution. In the subsequent step, the sub-series are fed into the ANN and the output of each sub-series is obtained. In the third step, the outputs obtained by passing each sub-series through the ANN are added to obtain the final output. In this study, Daubechies order 1(db1) mother wavelets are used to decompose input signal up to level 3.
2.6.3 GA-ANN
We have used genetic algorithm techniques to determine the optimal biases as well as the weights of the ANN, instead of using the back-propagation optimization technique. Similar to the approach used in pure ANN, different combinations of number of hidden nodes and number of input nodes were used to create the ANN models, which were then optimized using GA. The steps followed are:
-
1.
The architecture of the ANN was created by fixing the number of delays, hidden and output nodes.
-
2.
A population of 200 solutions was randomly generated.
-
3.
Each of the solution sets was used to obtain the biases and weights of the ANN, and output was obtained using each solution.
-
4.
The fittest individuals of the current generation were used to create the next generation by crossover method.
-
5.
Some of the individuals were mutated to obtain the next generation.
-
6.
Some migrations were also allowed between generations to increase diversity of the solutions.
-
7.
Steps (3) to (6) were repeated till the solutions stopped improving.
-
8.
The best solution was used to obtain the final output from the ANN.
2.6.4 Pure ANFIS
-
ANFIS models with the following parameters were created:
-
Number of inputs: 4
-
Number of input membership function: 2
-
The models made use of hybrid algorithm to use as optimization method
-
Input membership function types for grid partitioning FIS generation used were:
-
triangle-shaped (trimf)
-
trapezoid-shaped (trapmf)
-
Gaussian curve (gaussmf)
2.6.5 DWT-ANFIS
On the basis of results evaluated by ANFIS alone, it can be said that it fails to deal with dynamic time series data directly; therefore, pre-processing of data is required before giving to ANFIS. Here DWT plays an important role of improving the performance of this model. Initially data are decomposed by using Daubechies wavelet (DB1) at three levels. Then a check is performed for every signal for randomness. Signal containing random points that scale high in number is termed to be noisy signal which is unpredictable. This noisy signal is hence removed from analysis, because it creates inaccurate results.
2.6.6 GA-ANFIS
Genetic algorithm was implemented to optimize weights and biases of ANFIS. Similar to the approach used in pure ANFIS, a structure was created, which was then optimized using GA. The steps followed were:
-
1.
The architecture of the ANFIS was created by fixing the number of input membership function example 2.
-
2.
A population of 200 solutions was randomly generated.
-
3.
Each of the solution sets was used to evaluate the weights and biases of the ANFIS, and output was obtained using each solution.
-
4.
The fittest individuals of the current generation were used to create the next generation by crossover method.
-
5.
Some of the individuals were mutated to obtain the next generation.
-
6.
Some migrations were also allowed between generations to increase diversity of the solutions.
-
7.
Steps (3) to (6) were repeated till the solutions stopped improving.
The best solution from the pool of solutions was then used to obtain the final output from the ANFIS model.
3 Results and discussions
The six models developed were compared by determining the RMSE, R square and IA values of the forecasted data. The results of the different ANN-based models are given in Tables 1, 2 and 3. On the basis of the values obtained, it can be observed that when the number of input delays is less, the performance of pure ANN and GA-ANN is comparable. The performance of DWT-ANN model is poorer than the others. However, when the number of input delays is increased it can be observed that by using genetic algorithm to determine the optimal weights and biases of the neural network, a lower RMSE and a higher IA and R square values can be obtained. The results of wavelet-based hybrid ANN models were also better than pure ANN models. The RMSE, R square and IA values for different ANFIS-based models are given in Tables 4, 5 and 6. In the case of ANFIS-based models also it has been observed that the performance is improved when the data are pre-processed using wavelet-based signal processing technique. The best results of different ANN- and ANFIS-based hybrid models are given in Table 7. Table 7 shows that GA-ANN-based hybrid model has the lowest RMSE value, highest IA value and R square value. It is further observed that the overall performances of all the hybrid models in general are better than that of pure models. The authors in this paper have validated the usability of different AI models in time series prediction of waste generation. There are different methods to forecast waste generation such as regression analysis and material flow analysis; however, due to the dearth of the availability of such complex data, time series method becomes preferable. Though work has been done previously on the AI-based time series forecasting of waste generation, the hybrid ANFIS algorithms and the GA optimized ANN have been used for the first time.
4 Conclusion
A fundamental step in designing of an effective garbage management system is to predict the amount of waste that a city will generate. Determination of the volume of waste beforehand will result in the proper planning of landfill sites, recycling units, development as well as operation of garbage collection infrastructure. In a metropolitan city like New Delhi, it is of extreme importance to plan in advance, so that the handling of the waste generated can be properly managed and environmental and health hazards can be prevented. As this study presents, artificial intelligence-based techniques that can be successfully employed for forecasting the volume of the waste. In this paper, six models ANN ANFIS GA-ANN GA-ANFIS DWT-ANN and DWT-ANFIS were successfully evaluated to determine their effectiveness in MSW forecasting. If ranked in accordance with the performance of models, GA-ANN is found to be the most accurate one.
References
Abbasi M, El Hanandeh A (2016) Forecasting municipal solid waste generation using artificial intelligence modelling approaches. Waste Manag 56:13–22. https://doi.org/10.1016/j.wasman.2016.05.018
Badrzadeh H, Sarukkalige R, Jayawardena A (2013) Impact of multi-resolution analysis of artificial intelligence models inputs on multi-step ahead river flow forecasting. J Hydrol 507:75–85. https://doi.org/10.1016/j.jhydrol.2013.10.017
Beale MH, Hagan MT, Demuth MH (2010) Neural network toolbox TM 7, user’s guide. MathWorks Inc., Natick
Beigl P, Lebersorger S, Salhofer S (2008) Modelling municipal solid waste generation: a review. Waste Manag 28(1):200–214. https://doi.org/10.1016/j.wasman.2006.12.011
Buenrostro O, Bocco G, Vence J (2001) Forecasting generation of urban solid waste in developing countries—a case study in Mexico. J Air Waste Manag Assoc 51(1):86–93. https://doi.org/10.1080/10473289.2001.10464258
Chhay L, Reyad MAH, Suy R, Islam MR, Mian MM (2018) Municipal solid waste generation in China: influencing factor analysis and multi-model forecasting. J Mater Cycles Waste Manag 20:1–10
Conroy G (1991). Handbook of genetic algorithms by Lawrence Davis (ed), Chapman & Hall, London, pp 385, £32.50. Knowl Eng Rev, 6(04):363. https://doi.org/10.1017/s0269888900006068
Dixit M, Kumar H (2015). Tata McGraw Hill Education Private Limited. https://doi.org/10.4135/9781473974463
Estay-Ossandon C, Mena-Nieto A, Harsch N (2018) Using a fuzzy TOPSIS-based scenario analysis to improve municipal solid waste planning and forecasting: a case study of Canary archipelago (1999–2030). J Clean Prod 176:1198–1212
Jaipuria S, Mahapatra S (2014) An improved demand forecasting method to reduce bullwhip effect in supply chains. Expert Syst Appl 41(5):2395–2408. https://doi.org/10.1016/j.eswa.2013.09.038
Jalili M, Noori R (2008) Prediction of municipal solid waste generation by use of artificial neural network: a case study of Mashhad. Int J Environ Res 2:13–22
Jang J (1993) ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst Man Cybern 23(3):665–685. https://doi.org/10.1109/21.256541
Kannangara M, Dua R, Ahmadi L, Bensebaa F (2018) Modeling and prediction of regional municipal solid waste generation and diversion in Canada using machine learning approaches. Waste Manag 74:3–15
Kant A, Suman PK, Giri BK, Tiwari MK, Chatterjee C, Nayak PC, Kumar S (2013) Comparison of multi-objective evolutionary neural network, adaptive neuro-fuzzy inference system and bootstrap-based neural network for flood forecasting. Neural Comput Appl 23(S1):231–246. https://doi.org/10.1007/s00521-013-1344-8
Kumar A (2013) Existing Situation of Municipal Solid Waste Management in NCT of Delhi, India. Int J Soc Sci 1(1):324–338
Kuusisto S, Lehtokangas M, Saarinen J, Kaski K (1997) Short term electric load forecasting using a neural network with fuzzy hidden neurons. Neural Comput Appl 6(1):42–56. https://doi.org/10.1007/bf01670151
Nabavi-Pelesaraei A, Bayat R, Hosseinzadeh-Bandbafha H, Afrasyabi H, Chau KW (2017) Modeling of energy consumption and environmental life cycle assessment for incineration and landfill systems of municipal solid waste management-A case study in Tehran Metropolis of Iran. J Clean Prod 148:427–440
Navarro-Esbrı́ J, Diamadopoulos E, Ginestar D (2002) Time series analysis and forecasting techniques for municipal solid waste management. Resour Conserv Recycl 35(3):201–214. https://doi.org/10.1016/s0921-3449(02)00002-2
Nayak P, Sudheer K, Rangan D, Ramasastri K (2004) A neuro-fuzzy computing technique for modeling hydrological time series. J Hydrol 291(1–2):52–66. https://doi.org/10.1016/j.jhydrol.2003.12.010
Noori R, Abdoli M, Ghasrodashti AA, Jalili Ghazizade M (2009) Prediction of municipal solid waste generation with combination of support vector machine and principal component analysis: a case study of Mashhad. Environ Prog Sustain Energy 28(2):249–258. https://doi.org/10.1002/ep.10317
Pany PK, Ghoshal SP (2015) Dynamic electricity price forecasting using local linear wavelet neural network. Neural Comput Appl 26(8):2039–2047. https://doi.org/10.1007/s00521-015-1867-2
Rimaitytė I, Ruzgas T, Denafas G, Račys V, Martuzevicius D (2012) Application and evaluation of forecasting methods for municipal solid waste generation in an eastern-European city. Waste Manag Res 30(1):89–98. https://doi.org/10.1177/0734242x10396754
Singh D, Satija A (2016) Prediction of municipal solid waste generation for optimum planning and management with artificial neural network—case study: Faridabad City in Haryana State (India). Int J Syst Assur Eng Manag 9(1):91–97. https://doi.org/10.1007/s13198-016-0484-5
Singh LP, Challa RT (2015) Integrated Forecasting Using the Discrete Wavelet Theory and Artificial Intelligence Techniques to Reduce the Bullwhip Effect in a Supply Chain. Glob J Flex Syst Manag 17(2):157–169. https://doi.org/10.1007/s40171-015-0115-z
Siying W, Jinlong Z, Zhicheng Li (1997) A supplier-selecting system using a neural network. In: IEEE international conference on intelligent processing systems (Cat. No.97TH8335). https://doi.org/10.1109/icips.1997.672825
Sodanil, M, Chatthong P (2014) Artificial neural network-based time series analysis forecasting for the amount of solid waste in Bangkok.In: Ninth international conference on digital information management (ICDIM 2014). https://doi.org/10.1109/icdim.2014.6991427
Wang W, Chau K, Cheng C, Qiu L (2009) A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J Hydrol 374(3–4):294–306. https://doi.org/10.1016/j.jhydrol.2009.06.019
Wei S, Song J, Khan NI (2011) Simulating and predicting river discharge time series using a wavelet-neural network hybrid modelling approach. Hydrol Process 26(2):281–296. https://doi.org/10.1002/hyp.8227
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Soni, U., Roy, A., Verma, A. et al. Forecasting municipal solid waste generation using artificial intelligence models—a case study in India. SN Appl. Sci. 1, 162 (2019). https://doi.org/10.1007/s42452-018-0157-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-018-0157-x