An Innovative Approach in Inspecting a Damped Mathieu Cubic–Quintic Duffing Oscillator

Abstract

Purpose

The objective of the present study is to analyze a damped Mathieu–cubic quintic Duffing oscillator as a parametric nonlinear oscillatory dynamical system. This equation has multiple applications in diverse fields, including optics, quantum physics, and general relativity. There are multiple concerns related to periodic motion and the analysis of boundary-value problems with elliptic symmetries. The current effort aims to determine the frequency amplitude of parametric nonlinear issues.

Method

The non-perturbative approach (NPA) is employed to transform the nonlinear ordinary differential equation (ODE) into a linear equation. The derivation of the approximate solutions is achieved without relying on typical perturbation approaches, separate from the series expansion. Hence, the objective of this study is to depart from traditional perturbation methods and acquire approximated solutions for minor amplitude parametric components without imposing any limitations. Furthermore, the technique is extended to ascertain optimal solutions for the nonlinear large amplitude of fluctuation.

Results

The current approach allows for rapid estimation of the frequency-amplitude relationship in order to attain successive approximations of the solutions for parametric nonlinear fluctuations. A validation is obtained for the derived parametric equation, demonstrating a high level of agreement with the original equation. An analysis of stability behavior is conducted in multiple scenarios. In addition, the Floquet theory is used to examine the transition curves.

Conclusion

The current technique is characterized by its clear principles, making it practical, user-friendly, and capable of achieving exceptionally high numerical precision. The current approach is highly beneficial for addressing nonlinear parametric problems due to its ability to minimize algebraic complexity during implementation.

Introduction

The nonlinear or even linear parametric differential formulas of the Mathieu type have garnered a great deal of interest due to their abundant possible usages. Many properties of the Mathieu differential equation can be presumed from the general theory of ordinary differential equations (ODEs) with periodic coefficients, for example, the Floquet theory. Mathieu’s differential equations appear in a wide range of contexts in engineering, physics, and applied mathematics. This well-known equation requires careful consideration and in-depth research under various circumstances because it has numerous applications in physics and chemistry. The theory of ODEs with periodic coefficients, sometimes known as the flux theory, yields certain aspects of the Mathieu differential formula. There are several associations in practical mathematics, physics, and engineering of Mathieu's differential equations. Numerous characteristics of the Mathieu differential equation have been determined by means of the general theory of periodic coefficients in ODEs. For a long time, scientists have used several perturbation approaches to examine the analytical solutions associated with these equations [1,2,3,4]. Following the multiple scales method, the perturbation methodology is based on the idea of a minor parameter [5, 6]. Finding an accurate analytical solution to nonlinear issues has been a research area since solving nonlinear ODEs was more difficult than solving linear ones. Consequently, the perturbation technique is the only way to analyze any linear equation with periodic forces. Furthermore, the presence of a nonlinear state in ODEs poses numerous challenges, particularly when the periodic coefficients are included in the nonlinear state. Using a different way to achieve an estimated solution without consuming any of the existing perturbation approaches is one of the main objectives of this work. To find an approximation answer, the perturbation methods are difficult. Mathieu's nonlinear equation is the case examined here, with and without damping forces. Away from the consequences of the nonlinearity, it can be explained using perturbation systems, particularly because of the existence of periodic actions. Introducing a novel approach for obtaining a quasi-perfect answer is seen as a significant accomplishment that benefits both the technical and physical domains. As-well known, several mechanical systems, including suspension bridges, aircraft wings, and automotive suspensions, have non-linear oscillatory behavior. Comprehending the frequency correlation aids in the creation of systems that prevent resonance frequencies, this can result in structural collapse. Buildings and structures are designed to be able to survive earthquakes, which frequent cause nonlinear oscillations. The circulatory system in humans displays non-linear oscillating behavior. Examining these dynamics might enhance comprehension of cardiac problems and facilitate the advancement of medical apparatuses such as pacemakers, which are architectural structures and performance venues are specifically engineered to control the propagation of sound waves, which frequently entail non-linear vibrations. Thorough examination guarantees high-quality and minimizes noise pollution.

Although the nonlinearity appears to have numerous practical applications, it has been challenging for researchers and theoretical physicists to reach an exact solution or even one that is extremely close to the accurate one. They usually seem to have choices, even if their motivation comes from their own aims. Consequently, asymptotic explanations of different nonlinear ODEs have been the concern of several mathematicians. The smallest factor procedure and the averaging approach were used to demonstrate weak nonlinear equations [7]. The homotopy perturbation technique (HPM) is used for obtaining precise asymptotic calculations in the case of low-intensity sounds. The oscillation systems' solutions are also found by using the various time scales approach. Unfortunately, employing this low quantity in both techniques produced inconsistent outcomes [8]. In any asymptotic or perturbation procedure, determining the small parameter required to express the fundamental equations more practically and realistically is an essential initial step. Recently, there has been an increase in the attractiveness of many HPM-based techniques for predicting a variety of nonlinear ODEs and bringing them somewhat nearer to their answers [9]. If the initial guess did not match the technique used to answer the investigation, the method would deviate and fail to produce the desired outcomes. These methods relied on the preliminary estimate of the solution. The HPM is used in analyzing analytical approximations for magnetic spherical pendulums [10]. Even with the apparent numerous developments, the HPM proved to be challenging to run in the case of non-conservative oscillators. The extended HPM's analytical capability for nonlinear vibration theory is guaranteed [11]. It focused on linked damping nonlinear oscillators across many categories. The examples in each category might serve as heuristic explanations or as models for additional applications. He's frequency formulation (HFF) is an easy and effective way to construct a conservation nonlinear oscillator when working with nonlinear oscillator difficulties [12]. The inception of the HFF is attributed to Prof. He, a Chinese mathematician. An examination of the Duffing oscillator (DO) in vibration periodic behavior was carried out under generalized initial conditions [13]. The HFF is found to be mathematically straightforward, physiologically perceptive, and practically useful through numerical testing. Engineers may quickly and accurately analyze nonlinear vibration systems using the HFF by applying the unique method described in the study. To modify the HFF in a novel way, it is suggested to divide the oscillators into two extreme situations [14]. There is good agreement when the approximate and exact frequencies for different amplitudes are examined. The Hamiltonian function based on the HFF received remarkable interest since it simplified the computational understanding of a complicated nonlinear vibration system. As an example, the cubic–quintic DO was used to demonstrate how perfectly accurate and simple the calculation is. A straightforward method for solving the cubic–quintic DO is presented [15]. The technique offered a very effective and somewhat accurate way to calculate a nonlinear conservative oscillator's frequency. A presentation and demonstration of the streamlined HFF for nonlinear oscillators are offered [16]. It is advised to modify the HFF if there was any nonlinearity [17]. A straightforward frequency formula in fractal systems is published and derived from the HFF [18]. The straightforward computation and reliable outcomes combined to create a useful tool for in-depth research on fractal vibration phenomena. The non-Newtonian fluids were fundamental in many industries, such as technology and manufacturing. For this reason, research into these fluids is very interesting. The nonlinear stability analysis focused on a few non-Newtonian fluids. For the composition of some dynamical systems with a flat disrupted interface, an illustration was built. The primary objective of this theoretical examination is to use the NPA as a complement to our recent findings [19,20,21,22,23,24,25,26,27,28,29,30].

Electronic circuits containing elements such as diodes and transistors demonstrate non-linear characteristics. Utilizing nonlinear oscillatory analysis is beneficial for the purpose of building stable circuits and gaining insights into signal distortions in communication systems. MEMS [31] which include sensors and actuators frequently function in nonlinear oscillatory environments. Accurate determination of frequency and amplitude is essential for ensuring the dependability and effectiveness of the system. Wind turbines' blades undergo nonlinear oscillations as a result of fluctuating wind velocities. Gaining a comprehensive understanding of these dynamics is crucial for maximizing energy capture and guaranteeing the stability and strength of the structure. Control systems for spacecraft drones and robotic arms have to efficiently handle nonlinear dynamics. Nonlinear oscillation modeling guarantees the stability and precise performance of these systems, even when operational conditions change. Early diagnosis and maintenance of faults in structures, such as satellite antennas and robotic components, can be facilitated by identifying and forecasting their nonlinear dynamic behavior. Brain activity encompasses non-linear oscillations that can be analyzed to gain insights into neurological illnesses and improve brain-computer interface technologies. Buildings and bridges incorporate vibrations dampening devices to regulate oscillations resulting from wind or human activities [15, 32, 33]. In this work, we will demonstrate that the previously outlined approach can be used to find both the frequency and the phase space solutions of the parametric oscillation [17]. Therefore, the current study is an additional application of the NPA to analyze the nonlinear cubic–quintic Duffing Mathieu oscillator. The approach is useful and promising, and it can be used in a range of parameterized differential equation categories. The method puts forth an oscillator attempt solution that satisfies the initial requirements. The general frequency of the system is represented by an unidentified value in the solution, and it is possible to compute this frequency connection efficiently and straightforwardly. This approach has successfully converted the nonlinear formula into a fully resolvable linear formula in the lack of parameterized force. This method is primarily presented for solving the nonlinear Mathieu's formulation. The products were quite good when compared to the numerical solution of the nonlinear Mathieu's equation. This demonstrated the validity of the employed methodology. To clarify the presentation of the manuscript, the remainder of the paper is organized as follows; the damped Mathieu cubic–quintic DO is presented in “Damped Mathieu Cubic–Quintic DO”. This section also involves a special case. The analysis concerning arbitrary excited frequency is introduced in “Analysis of an Arbitrary Excited Frequency $\Omega$”. An enhancement approximate solution is provided in “Enhanced of the NPA”. The inclusion of the damping influence is given in “Frequency Formula Due to the Presence of the Damping Term”. The analysis of the transition curves is provided in “Transition Curves and Stability/Instability Zones”. Lastly, the key outcomes are summarized in “Conclusions”.

Damped Mathieu Cubic–Quintic DO

Noteworthy uses of parameterized excitation equations are found in oscillatory systems due to the application of external forces. The Mathieu equation is frequently applied to this objective in a variety of domains because it effectively expresses important aspects of the phenomenon. The linear Mathieu equation has been studied extensively for a long time, and many properties of its solutions have been fully understood [1, 5, 6, 8]. Often referred to as the cubic quintic DO, the parameterized damping nonlinear Mathieu equation is described simply as:

$$\ddot{y} + 2\mu \dot{y} + \left( {a - 2q\cos \Omega t} \right)y + Qy^{3} + Ry^{5} = 0,$$

(1)

where $\mu ,\,a,\,q,\,{\text{and}}\,\,\Omega$ are the damped coefficient, square of the natural frequency, excitation amplitude, and frequency, respectively. Additionally, the parameters $Q,\,{\text{and}}\,\,R$ characterize the cubic and quintic DO coefficients, respectively.

The suggested initial conditions (ICs) of Eq. (1) are usually considered as:

$$y(0) = A,\,\,{\text{and}}\,\,\dot{y}(0) = 0.$$

(2)

While looking for the correct reply, particular considerations must be given to the dampening forces in Eq. (1). Consequently, we will begin by examining the conservative situation, whereby the damping forces' influence vanishes. The Mathieu cubic–quintic DO without damping is expressed as follows:

$$\ddot{y} + \left( {a - 2q\cos \Omega t} \right)y + Qy^{3} + Ry^{5} = 0.$$

(3)

Equation (3) can be written as:

$$\ddot{y} - 2q\cos \Omega ty + f(y) = 0,$$

(4)

where $f(y) = ay + Qy^{3} + Ry^{5}$.

One seeks for the resolution of Eq. (3) as a sequence of $q$ in the standard perturbation theory. Using the Lindstedt–Poincare perturbation approach, the non-linear Mathieu formulation with quadratic and cubic non-linearity was solved with small amplitude [34]. A variational technique was used [35] to investigate the dampened linear or nonlinear Mathieu equation. To explain the Mathieu formula, a variational iteration approach, as specified in Eq. (3), was applied without a tiny parameter [36]. A two-variable expansion was used to study a system of nonlinear Mathieu equations [37]. In all of the previous articles, the smallness parameter made a restriction on the periodic coefficient. The fundamental idea of perturbation theory is to evaluate the approximate solution as a sequence of a small factor [5, 6, 38,39,41]. We often have no notice in the large factor domain of the model under investigation, which is a clear shortcoming in the perturbation approach. Several approaches have been proposed to overcome this problem: either to find an "artificial" expansion parameter to obtain additional information on the "physical" parameter, or to improve the sequence convergence by resuming (expending, for instance, Pada approximants). An attempt has been made to obtain an estimated answer for Eq. (3) with the NPA in this instance.

A trial solution of the DO is assumed, as given in Eq. (3) in the absence of the parametric coefficient $q$, in the following form:

$$u = A\cos \omega t,$$

(5)

where $\omega$ is the total frequency to be determined later.

An elementary frequency concept for nonlinear oscillators is presented, shown, and subsequently proposed for change. An introduction is made to a fractal vibration occurring in a porous medium, and its attribute of having a low frequency is explained using the frequency formulation. It demonstrates that the inertia force in a fractal space is equal to the combined effect of the inertia force and the damping impact in the conventional differential approach [32]. Following El-Dib [17] and Moatimid et al. [19,20,21,22,23,24,25,26,27,28,29,30], the HFF for the odd function $f(y)$ is given as follows:

$$\omega^{2} = \int\limits_{0}^{2\pi /\omega } {uf(u)\,dt/\int\limits_{0}^{2\pi /\omega } {u^{2} dt} } .$$

(6)

Combining Eq. (6) with the definition of the function $u(t)$, one gets

$$\omega^{2} = a + \frac{3}{4}QA^{2} + \frac{5}{8}RA^{4} .$$

(7)

Therefore, it is advantageous to linearly transform the Mathieu-DO as given in Eq. (3) because calculating nonlinear differential formulations is more difficult than computing linear ones. The procedure's basic idea is to substitute a linear differential formula with an explicitly reliant time component to obtain the usual linear Mathieu equation. Now, combining Eqs. (3) and (7), one gets

$$\ddot{y} + \left( {\omega^{2} - 2q\cos \Omega t} \right)y = 0.$$

(8)

The parameter $\omega^{2}$ may be addressed as the Duffing frequency of the considered system.

The oscillation of the non-parametric nonlinear frequency in the absence of the factor $q$ is suggested by the HFF [17, 19,20,21,22,23,24,25,26,27,28,29,30]. At this point, the linearized version of the nonlinear Mathieu Eq. (3) has been reduced to the nonlinear natural frequency, which is represented by frequency in Eq. (7). The properties of Mathieu equation Eq. (8) are well known [1, 39, 42]. As given in Eq. (5), the nonlinear natural frequency $\omega$ has been determined using the trial solution. As well known, Eq. (8) is a linear homogeneous ODE and its solution is very difficult because of the presence of the periodic term. Therefore, it has no exact solution and the perturbation technique is needed. In this instance, the frequency as given in Eq. (7) of the previous DO needs to be adjusted to account for the influence of the amplitude $q$. Subsequently, in the next subsection, an attempt has been made to analyze Eq. (8) along with the way of the HFF.

Frequency Formula Due to the Presence of the Parametric Excitation

It is preferable to extend the earlier technique to Eq. (8) which has periodic coefficients. Equation (8) may be rewritten as follows:

$$\ddot{y} + F(y,t) = 0,$$

(9)

such that the linear parametric function is given as

$$F(y,t) = \left( {\omega^{2} - 2q\cos \Omega t} \right)y.$$

(10)

The absence of the factor $q$ in Eq. (10) produces an analysis as previously given [17, 19,20,21,22,23,24,25,26,27,28,29,30]. Here, this technique will be lengthy to contain the influence of the parametric nonlinear oscillator. In the light of the conventional procedure, we aim to transform Eq. (8) to the following equation:

$$\ddot{y} + \varpi^{2} (\Omega )y = 0.$$

(11)

It should be mentioned that the whole frequency $\varpi$ concerning the parametric excitation $\Omega$ can be calculated by using the function provided in Eq. (10). It is important to remember that Eq. (11) shows that a straightforward linear simple harmonic oscillation, with constant frequency $\varpi^{2} (\Omega )$, can be used to analyze the nonlinear Mathieu-DO. Actually, the method accustomed to determining the whole oscillation in the absence of the factorial excitation differs from that used in its presence. Consequently, the following recommended solution may be provided to determine the required frequency:

Once more, it is required to achieve another simple harmonic motion as given in the following process:

$$v(t) = B\cos \varpi t,\,\,\,ICs\,\,\,\,\,v(0) = B,\,\,\,{\text{and}}\,\,\,\,\dot{v}(0) = 0,$$

(12)

where the oscillation amplitude is denoted by the constant $B$.

It should be noted that no approximation has been previously established. The procedure listed below can be used to determine the necessary frequency $\varpi^{2} (\Omega )$. When Eqs. (9) and (11) are compared, the following sort of error results in

$$E(\varpi^{2} ) = \left| {F(y,t) - \varpi^{2} (\Omega )y(t)} \right|.$$

(13)

The average squared error, as used in statistics, gives the average or mean of the square of the alteration concerning the expected and actual values. With this preparation, one gets

$$\overline{E}^{2} (\varpi^{2} ) = \int\limits_{0}^{2\pi /\varpi } {\left( {F(y,t) - \varpi^{2} (\Omega )y(t)} \right)^{2} } dt.$$

(14)

The minimal amount necessitates that

$$\frac{d}{{d\varpi^{2} }}\overline{E}^{2} (\varpi^{2} ) = \frac{d}{{d\varpi^{2} }}\int\limits_{0}^{2\pi /\varpi } {\left( {\varpi^{4} (\Omega )y^{2} (t) - 2\varpi^{2} (\Omega )y(t)F(y,t) + F(y,t)^{2} } \right)\,dt = 0} .$$

(15)

A proposal is made to incorporate a fractional alteration using the Riemann–Liouville time-fractional derivative in order to interpretation for the discontinuous period. The equation is then shortened to a fractional nonlinear Schrödinger equation using the wave-train explanation. Finally, the equation is transformed into a damping DO. A potential solution to address the damping term is to make effective modifications to the HPM as previously proposed [43]. The simplification of the preceding relation indicates that the formulation $F(y,t)$ is independent of the oscillation $\varpi$. Therefore, one gets

$$\varpi^{2} (\Omega )\int\limits_{0}^{2\pi /\varpi } {y^{2} (t)\,dt - \int\limits_{0}^{2\pi /\varpi } {y(t)F(y,t)\,dt = 0} } .$$

(16)

It follows that

$$\varpi^{2} (\Omega ) = \int\limits_{0}^{2\pi /\varpi } {y(t)F(y,t)\,dt/\int\limits_{0}^{2\pi /\varpi } {y^{2} (t)\,dt} } .$$

(17)

Remember that relation (17) is comparable to what was previously obtained without the excitation influence [17, 19,20,21,22,23,24,25,26,27,28,29,30]. The oscillation equivalent to the appropriate sample solution that matches the ICs can be found in carrying out the beforehand designated integrals. One benefit of this formulation is that it makes the frequency analysis possible within a specified time. The simplest and most effective method for uniquely determining the frequency is represented by the formula outlined above. The accuracy of the frequency formula is confirmed by the aforementioned analysis procedure.

Analysis of a Special Case

As a particular example of the stimulated frequency, one can assume that $\Omega = \omega$ in the present subsection. We may reduce the Mathieu provided in Eq. (8) to the following particular Mathieu equation according to these exceptional situations:

$$\ddot{y} + \left( {\omega^{2} - 2q\cos \omega t} \right)y = 0.$$

(18)

The resonance case is observed to arise from the special situation in the perturbation analysis [5, 6]. However, because the trial solution is established with a total frequency, the resonance case is not functional in the NPA. The resonant situation was addressed by using the pioneer perturbation technique, known as the multiple-time scales. Regrettably, the NPA prohibits us from engaging in a discussion regarding this subject. In a recent publication, the concept of multiple-time scales can be utilized to analyse the resonance scenario in a linear ODE of similar nature.

As previously supposed, the direction here is to consider a harmonic potential as follows:

$$\ddot{w} + \varphi^{2} (\omega )w = 0.$$

(19)

The ICs of Eq. (19) is usually considered as:

$$w(0) = C,\,\,{\text{and}}\,\,\dot{w}(0) = 0.$$

(20)

The following guessing solution, due to Eq. (19) with ICs (20), is recommended:

$$w(t) = C\cos \varphi t,$$

(21)

where $\varphi$ is an unknown constant, which represents the total frequency in this case.

By simply adding Eq. (20) to the frequency formula provided in Eq. (17), and $\varphi$ can be found with ease. Using the MS, the desired outcome is obtained in the following format:

$$\varphi^{2} = \frac{1}{8}\left( { - 8q + 5\omega^{2} + \sqrt {64q^{2} - 16q\omega^{2} + 9\omega^{4} } } \right).$$

(22)

Accordingly, the approximate answer is provided below:

$$w(t) = C\cos \sqrt {\frac{1}{8}\left( { - 8q + 5\omega^{2} + \sqrt {64q^{2} - 16q\omega^{2} + 9\omega^{4} } } \right)} \,t,$$

(23)

Equation (18) is a linear ODE with a periodic coefficient. Consequently, it lacks a precise solution. Fortunately, the NPA allows us to derive an alternate equation with constant coefficients, as shown in Eq. (19). Typically, it is essential to use the method of numerical computation for confirming the process. The MS has adopted this technique. Therefore, for greater convenience, the numerical evaluation of Eq. (18) is validated by the MS with the solution of Eq. (19) which is provided by Eq. (23) for an arrangement with a sample choosing system. Actually, Eq. (7) addresses the natural frequency. Consequently, the objective is represented by Fig. 1 with the following data:

Fig. 1

A comparative graph between the solutions of Eqs. (18) and (19)

$a = 3,Q = 0.1,R = 0.1,q = 0.01,\,\,{\text{and}}\,\,C = 1.0$.

It should be noted that, as shown from the MS, the absolute error is given by 0.177613. Since these analytical solutions are not limited to small amplitude standards, the evaluation of the numerical technique demonstrates that these findings are more precise.

As an improvement of the NPA, it enables us to inspect the stability examination of the given structure. Therefore, for further convenience, the stability diagrams are plotted for the comparative equation as given in Eq. (19). Figure 1 validates how this technique is a successful approach. Therefore, it is convenient to analyze the alternative linear ODE as given in Eq. (19) instead of the Mathieu cubic–quintic DO as given in Eq. (3) through the considered special case. The current model attempts to analyze nonlinear stability. As a result, this new technique is considered a skilful, simple, and successful process in this respect as opposed to the conventional ways. Many different kinds of nonlinear equations may be analyzed using this innovative method. Here, the stability criterion in the case of $\Omega = \omega$ maybe assumed in the form:

$$\varphi^{2} > 0.$$

(24)

In what follows, Figs. 2, 3, 4 and 5 are plotted to examine the stability diagram of condition (24), where $\varphi^{2}$ is drawn against the I.C. parameter as addressed as $C$. The constraint $\varphi^{2} > 0$ represents a transcendental inequality in the parameters $\,a,\,q,\,Q,R\,$, and $\,C$. The configuration of this circumstance is adopted with the aid of MS Version 12.0.0.0 to illustrate the stability shapes by scheming $\varphi^{2}$ against $C$ as exposed in Figs. 2, 3, 4 and 5 according to the data: $a = 3,Q = 0.1,R = 0.1,\,\,{\text{and}}\,\,q = 0.1$, which vary in each figure according to the studied parameter.

Fig. 2

Indicates the stability regions with the variation of $a$

Fig. 3

Indicates the stability regions with the variation of $q$

Fig. 4

Indicates the stability regions with the variation of $Q$

Fig. 5

Indicates the stability regions with the variation of $R$

The stable zones of a definite domain regarding the initial condition $C$ are shown in Figs. 2, 3, 4 and 5, where the stable regions are shown by the colored zones above the curves, whereas the white zone beneath the curves indicates the unstable area. In Fig. 2, the square of the natural frequency $a$ rises from 1.0 to 4.0, meanwhile the other parameters are kept fixed. Mechanical systems having periodic stiffness can have their vibrations modeled using the Mathieu equation. Examples include oscillating systems with regularly variable parameters, vibrations in rotating equipment, and stability study of structures subjected to periodic stresses. Regarding this, Fig. 2 illustrates the influence of the normal oscillation on the stability configuration. This graphic shows that when the natural frequency increases, the stable zones diminish significantly. Therefore, the small values of the initial natural frequency cause a more destabilizing influence.

The stable zones develop with the rise of the excitation factor $q$, as shown in Fig. 3. It is observed that when $q$ rises in a small range from 0.01 to 0.2, meanwhile the other parameters are retained fixed, the stable areas extend significantly. The intensity of the periodic excitation is closely related to this parameter. A larger excitation or periodic modulation is indicated by a greater value of $q$, which is in consistent with the stabilizing influence of this parameter. The excitation factor q and its impact on stability and resonance are significant in various applications, such as design and analysis of structures subject to periodic forces, Analysis of atomic and molecular systems under periodic fields, and Stability analysis of systems with periodically varying parameters.

Figures 4 and 5 are designed to illustrate the behavior of the system with the varying cubic and quintic Duffing coefficients $Q,\,{\text{and}}\,\,R$, respectively. The cubic and quintic Duffing coefficients extending the linear Mathieu equation to include the nonlinear terms and studying their effects on the system's dynamics. The Mathieu equation and its nonlinear extensions with Duffing coefficients are valuable in the analysis of systems exposed to periodic forces and nonlinear properties. Their applications cover many fields, providing critical insights into resonance, stability, and complex dynamical systems. It is seen from Figs. 4 and 5 that the stable regions are reduced with the rise of both $Q,\,{\text{and}}\,\,R$, which means that the nonlinear terms are considered unstable coefficients of the dynamical system. Such effect is logic due to the rising of the nonlinearity contribution.

Additionally, some PolarPlots graphs, which are obtained via the Command of MS, diagrams are graphed to guarantee the stability of the previously obtained solutions. Accordingly, Figs. 6 and 7 indicate the PolarPlot of the periodic solution as given in Eq. (23) through the time interval $\left[ {0,\,50\pi } \right]$ in light of the parameters $a$, and $q$ to demonstrate the function $w(t)$ in terms of the total frequency $\varphi$. Therefore, Fig. 6 are schemed according to the various values of the square of the natural frequency $a = 2.0,3.0,4.0$. It is shown from this figure that, along with the growth of $a$, the curvilinear loops get dispersed about the centre. This outcome is consistent with the destabilizing effect of this parameter.

Fig. 6

Displays the PolarPlot of $w(t)$ for different measures of the square of the natural frequency $a$

Fig. 7

Displays the PolarPlot of $w(t)$ for different measures of the square of the excitation amplitude $q$

Figures 7 is plotted according to the various measures of the excited amplitude $q = 0.01,\,0.05,\,0.1$, to determine the PolarPlot of the function $w(t)$ as denoted in Eq. (23) using the total frequency $\varphi$. The circular, linked curves in this simulation are symmetrically distributed around their centres. This dispersion gives an idea of the stable mode that these curves operate in. Depending on the impact of the influencing factors, the circulation of the intersecting plots grows or decreases. It is observed that the loops become more organized about the centre, which is in accordance with the stability impact of $q$ as shown in Fig. 3.

Analysis of an Arbitrary Excited Frequency $\Omega$

Now, the equivalent Eq. (9) of the cubic quintic Mathieu DO as given in Eq. (3) will be utilized once again to determine the full oscillation $\psi$ that enclosed the impact for any $\Omega$. The normalized procedure of the excited oscillation $\Omega$ is used by the periodic time $T$ to formulate this frequency as:

$$\Omega = \frac{\sigma }{T},$$

(25)

where the periodic time is addressed as: $T = \frac{2\pi }{\psi }$.

By using the same formula defined in Eq. (17), one can write

$$\psi^{2} (\Omega ) = \int\limits_{0}^{2\pi /\psi } {h(t)F(h,t)\,dt/\int\limits_{0}^{2\pi /\psi } {h^{2} (t)\,dt} } ,$$

(26)

where $h(t)$ is the trial solution of Eq. (9); in this general case, it can be evaluated from the equivalent equation:

$$\ddot{h} + \psi^{2} (\sigma )h = 0,\quad {\text{ICs}}\quad h(0) = D,\,\,{\text{and}}\,\,\dot{h}(0) = 0,$$

(27)

$$h(t) = D\cos \psi t.$$

(28)

Substituting from Eq. (28) into Eq. (26), one can get the total frequency in this general case as:

$$\psi^{2} (\sigma ) = - \frac{{4q( - 8 + \pi^{2} \sigma^{2} ){\text{Sin}} (\pi^{2} \sigma )}}{{\pi^{2} \sigma ( - 16 + \pi^{2} \sigma^{2} )}} + \omega^{2}$$

(29)

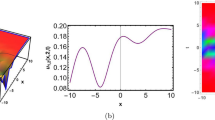
For more appropriateness, Fig. 8a is planned, utilizing the data $a = 3,Q = 0.1,$ $\sigma = 2,\,{\text{and}}\,\,D = 1.0$, $R = 0.1,q = 0.01,\,\,$ to compare the numerical solution of Eq. (9) (NS) with the approximate solution as given in Eq. (28) due to the NPA, concerning the formula (29) of $\psi^{2}$. One can observe the extreme congruency between the two solutions, where the absolute error equals 0.0865. Furthermore, Fig. 8b represents the intensified part of Fig. 8a in a very small range of time,$t = 10.0 \to 10.1$ to obtain the deviation between the NPA solution and the numerical solution of Eq. (9). This deviation does not appear unless a very small range of time is taken.

Fig. 8

a A comparative graph concerning the numerical evaluation of Eq. (9) and the NPA finding (26). b An intensified graph of Fig. 8a for a small interval of time from $t = 10.0$ to $t = 10.1$

An attempt is made to analyze the stability investigation. As said before, this new technique is considered a simple and successful process in this regard rather than the traditional ways. Here, the stability criterion for the case $\Omega = \frac{\sigma }{2\pi }\psi$ may be assumed in the form:

$$\psi^{2} > 0.$$

(30)

The configuration of the stable and unstable regions, in this case, is given by Figs. 9, 10, 11 and 12. These graphs are plotted to illustrate the stability criterion as given in (30), where $\psi^{2}$ is drawn against the initial amplitude $D$. Concerning the constraint $\psi^{2} > 0$, which is a transcendental inequality in the parameters $\,a,\,q,\,Q,R\,$, and $\,D$, the configuration of this circumstance is adopted with the aid of MS Version 12.0.0.0 to illustrate the stability shapes by scheming $\psi^{2}$ against $D$ as exposed in Figs. 9, 10, 11 and 12. The stable zones for a definite domain of the initial amplitude $D$ are exposed in Figs. 9, 10, 11 and 12, where the stable regions are shown by the colored zones above the curves, whereas the light zone beneath the curves indicates the unstable area.

Fig. 9

Indicates the stability regions with the difference of $q$

Fig. 10

Indicates the stability regions with the variation of $a$

Fig. 11

Indicates the stability regions with the variation of $Q$

Fig. 12

Indicates the stability regions with the variation of $R$

In Fig. 9, the stable zones develop with the rise of the excitation amplitude $q$, as shown by Fig. 9. One can observe that when $q$ rises in a small range from 0.01 to 0.2, meanwhile the other parameters are kept fixed, and the stable areas are slightly reduced. Moreover, Fig. 10 illustrates the impact of the square of the natural frequency $a$, which rises from 3.0 to 3.3, on the system’s stability. This figure proves that the augmentation of the natural frequency weakens the stability configuration. This figure indicates that when the natural frequency grows, the stable regions diminish considerably. It should be noted that the same mechanism, as shown in Figs. 2, and 3, in the previous special case gives the same behavior.

Figures 11 and 12 are designed to illustrate the behavior of the system with the varying cubic and quintic Duffing coefficients $Q$, and $\,R$, respectively. It is obtained that the stable regions are reduced with the rise of both $Q$, and $\,R$, which means that the nonlinear terms are considered unstable coefficients of the dynamical system. The same results are concluded in the special case $\Omega = \omega$ except with the impact of $q$, where the reverse happens. The identical mechanism, illustrated in Figs. 4 and 5 in the prior specific example, results in the same behavior.

Figures 13 and 14 indicate the PolarPlots of the periodic solution as given in Eq. (28) conclude the time interval $\left[ {0,\,50\pi } \right]$ according to the factors $a$, and $q$ to demonstrate the function $h(t)$ as defined according to Eq. (28) in terms of the total frequency $\psi$ that is defined in the form Eq. (29). Figure 13 is plotted according to the various values of the square of the natural frequency $a = 1.0,2.0,3.0$. It is shown from this figure that with the growth of $a$, the curved loops become more scattered and divided around the center. The destabilizing impact of this parameter is consistent with this result.

Fig. 13

Displays the PolarPlot of $h(t)$ for different measures of the square of the excited amplitude $q$

Fig. 14

Displays the PolarPlot of $h(t)$ for different measures of the square of the natural frequency $a$

Figure 14 is plotted according to the various measures of the excited amplitude $q = 0.01,\,0.05,\,0.1$, to determine the PolarPlot of the function $h(t)$ as given in Eq. (28) using the total frequency $\psi$. In this simulation, the circular connected curves have a symmetric distribution around their centers. An indication of the steady mode in which these curves work may be found in this dispersion. The circulation of the intersecting plots increases or decreases based on the influence of the affecting factors.

Enhanced of the NPA

The approximate solution that is given in Eq. (28) of the nonlinear Mathieu cubic quintic DO (9) is considered as a zero-order approximate solution. Now, to get an advanced more accurate approximate solution, the trial solution may be also enhanced to cover the first order for the same arbitrary case $\Omega = \frac{\sigma }{T}$, according to a small parameter $\varepsilon$, which will be evaluated later. This enhanced trail solution is assumed to improve the equivalent solution and the frequency, and could be formulated as [42]:

$$g(t) = E\cos \chi t + E\varepsilon (\cos 3\chi t - \cos \chi t).$$

(31)

One can easily find that this improved NPA still satisfies the initial conditions $g(0) = E$ and $\dot{g}(0) = 0$. Substituting from Eq. (31) into the previous formula (17), with the aid of MS, one can get the improved frequency $\chi (\sigma ,\varepsilon )$ as follows:

$$\begin{gathered} \chi^{2} (\sigma ,\varepsilon ) \hfill \\ = - \frac{{4q( - 73728(1 + 2( - 1 + \varepsilon )\varepsilon ) + 128\pi^{2} \sigma^{2} (85 + 16\varepsilon ( - 5 + 3\varepsilon )) + 8\pi^{4} \sigma^{4} ( - 5 + 3\varepsilon ) + \pi^{6} \sigma^{6} ){\text{Sin}} (\pi^{2} \sigma )}}{{\pi^{2} \sigma (1 + 2( - 1 + \varepsilon )\varepsilon )( - 144 + + \pi^{2} \sigma^{2} )( - 64 + \pi^{2} \sigma^{2} )( - 16 + \pi^{2} \sigma^{2} )}} + \omega^{2} \hfill \\ \end{gathered}$$

(32)

The unknown parameter $\varepsilon$ can be evaluated from the following minimization condition:

$$\frac{{d\chi^{2} }}{d\varepsilon } = 0,$$

(33)

which gives the value of $\varepsilon$ as a function of $\sigma$ as follows:

$$\varepsilon = - \frac{{ - 7808 + 216\pi^{2} \sigma^{2} - \pi^{4} \sigma^{4} + \sqrt {37371904 - 2250752\pi^{2} \sigma^{2} + 46400\pi^{4} \sigma^{4} - 368\pi^{6} \sigma^{6} + \pi^{8} \sigma^{8} } }}{{64( - 64 + \pi^{2} \sigma^{2} )}}.$$

(34)

Figure 15 is graphed to obtain the matching between the numerical evaluation of Eq. (9) (NS) and the approximate enhanced findings as given in Eq. (31) according to the NPA and concerning the formula (32) of $\chi^{2}$. One can notice the congruency between the two solutions, where the absolute error equals 0.073 with the usage data: $a = 3,Q = 0.1,R = 0.1,q = 0.01,\,\,\sigma = 2,\,{\text{and}}\,\,E = 1.0$.

Fig. 15

A comparative graph between the numerical evaluation of Eq. (9) and the enhanced NPA evaluation (31)

As shown in the previous cases, Figs. 16, 17, 18 and 19 are graphed to illustrate the stable zones for a specific domain of the starting amplitude $E$; the unstable area is indicated by the light zone under the curves, while the colored zones above the curves represent the stable regions.

Fig. 16

Indicates the stability regions in the enhanced case with the variation of $a$

Fig. 17

Indicates the stability regions in the enhanced case with the variation of $q$

Fig. 18

Indicates the stability regions in the enhanced case with the variation of $\sigma$

Fig. 19

Indicates the stability regions in the enhanced case with the variation of $Q$

Figure 16 shows the effect of the square of the natural frequency $a$, which increases from 1.0 to 4.0, while the other parameters are held constant in the stability of the system. This graph demonstrates how the stability configuration is weakened by increasing the natural frequency. This figure shows that the stable zones significantly decrease as the natural frequency increases, which ensures the destabilizing effect of this parameter. Moreover, Fig. 17 indicates that the stable zones diminish with the augmentation of the excitation amplitude $q$. One can notice that as $q$ rises from 0.01 to 0.4, meanwhile the other factors are kept immovable, and the stable areas are slightly reduced. It should be noticed that the preceding cases, depicted in Figs. 2, 3, 9, and 10, give the same behavior.

Figure 18 is plotted to demonstrate the influence of the feature $\sigma$, which replaces the excited frequency $\Omega$ as formulated in Eq. (25). From this figure one can notice that the stable regions grow with the rise of $\sigma$ from 1.0 to 4.0 as indicated through the figure. This means that the augmentation of this factor makes the system more stable concerning the value of $\chi^{2}$ defined by (32). Furthermore, Fig. 19 is designed to demonstrate the stability of the system with the varying cubic Duffing coefficient $Q$. It is obtained that the stable regions decrease with the rise of $Q$, which is consistent with the previous conclusions.

The PolarPlots of the periodic solution as given in the enhanced form (31) are indicated by Figs. 20 and 21 through the time interval $\left[ {0,\,50\pi } \right]$ with a varying of the parameters $a$, and $q$ to exhibit the function $g(t)$ as defined in Eq. (31) in terms of the total frequency $\chi$, which is deduced from the MS in the form Eq. (32). Figures 20 are designed according to the various values of the square of the natural frequency $a = 2.0,3.0,4.0$. It is shown from these figures that, with the growth of $a$, the curved loops distribution about the center are squeezed between accumulation and distraction in very amazing shapes. The destabilizing impact of this parameter is consistent with this result.

Fig. 20

Displays the polarplot of $g(t)$ for different measures of the square of the natural frequency $a$

Fig. 21

Displays the polarplot of $g(t)$ for different measures of the square of the excited amplitude $q$

Figures 21 are designed according to some measures of the excited amplitude $q = 0.01,\,0.05,\,0.1$, to display the PolarPlot of the function $g(t)$ as denoted in Eq. (31) using the total frequency $\chi$. The circular linked curves in this simulation exhibit a symmetric distribution around their centers. This dispersion may provide an indicator of the steady mode in which these curves operate. Depending on the impact of the contributing factors, the intersecting plots' circulation either rises or decreases.

Frequency Formula Due to the Presence of the Damping Term

In all of the above sections, the study tackles the case of non-damping Mathieu cubic quintic DO (3) and all its equivalent cases, as seen in "Damped Mathieu Cubic–Quintic DO", "Analysis of an Arbitrary Excited Frequency ", and "Enhanced of the NPA". Now, going back to the original damping Eq. (1), the current section is concerned with the existence of this term which was ignored previously. When the damping mechanism exists, the non-conventional oscillator structure involves energy waste. Since restraining is a fundamental component of the dynamic method of most real structures, which results in energy waste, these systems are not conservative. In addition to being more difficult to calculate and explain, the solution of a non-conservative oscillator sometimes involves complex consequences for which it might be difficult to formulate exact analytical solutions. The NPA, as examined in [44], represents a simple technique to examine some approximate analytical solutions for the nonlinear complicated equations like the damping Mathieu cubic quintic DO defined in Eq. (1).

The purpose of the current Section is to illustrate an equivalent solution of Eq. (1) by utilizing the same technique followed above with the suitable strategy. Equation (1) can be re-formulated in the form:

$$\ddot{y} + 2\mu \dot{y} + \left( {\omega^{2} - 2q\cos \Omega \,t} \right)y = 0,$$

(35)

where $\omega^{2}$ is the natural frequency that is defined in Eq. (7), and $\mu$ is the damping parameter.

In this case, Eq. (35) may be put into the standard normal form. Consequently, it is possible to propose the following transformation:

$$y = e^{ - \mu \,t} \lambda (t),$$

(36)

where $\lambda (t)$ is a required time periodic function to be evaluated.

Substituting from Eq. (36) into Eq. (35), one can get the differential equation that governs $\lambda (t)$ as:

$$\ddot{\lambda } + \left( {\delta^{2} - 2q\cos \Omega \,t} \right)\lambda = 0,$$

(37)

which is the ordinary Mathieu formulation with a natural oscillation $\delta$ that is produced by:

$$\delta^{2} = \omega^{2} - \mu^{2} .$$

(38)

Now, following NPA, one can suppose the solution of Eq. (37) as the basic form:

$$\lambda (t) = F\cos \gamma \,t.$$

(39)

By utilizing Eq. (17), the total frequency $\gamma$ is estimated and deduced in the form:

$$\gamma^{2} (\sigma ) = \omega^{2} - \mu^{2} - \frac{{4q( - 8 + \pi^{2} \sigma^{2} ){\text{Sin}} (\pi^{2} \sigma )}}{{\pi^{2} \sigma ( - 16 + \pi^{2} \sigma^{2} )}}.$$

(40)

Figures 22, 23, 24 and 25 are plotted to examine the compatibility between the numerical solutions of the original damping Mathieu Eq. (1) and the NPA solutions in different cases of the limit constant $F$, which equals $\lambda (0)$, with the data; $a = 3,Q = 0.1,R = 0.1,q = 0.01,\,\,\sigma = 5,\,\,\,{\text{and}}\,\,\mu = 0.1$. From Figs. 22, 23 and 24, one can observe that the convergence between the numerical evaluation of Eq. (1) and the NPA finding defined by Eq. (39) increases with the rise of $F$, where the absolute error when $F = 1$ equals 0.1273, as seen in Fig. 22. By contrast, the absolute error when $F = 2$ equals 0.0808, as seen in Fig. 23, and the absolute error when $F = 5$ equals 0.054, as seen in Fig. 24. Furthermore, Fig. 25 is graphed to examine the convergence between the numerical evaluation of the equivalent Mathieu formulation (35) and the NPA solution (39) with the same data used in Fig. 22. It is found that the convergence is bigger than the case discussed in Fig. 22, where the absolute error examined from Fig. 25 equals 0.066, which is a good result that indicates the significance of the NPA in this regard.

Fig. 22

A comparative graph among the numerical evaluation of Eq. (1) and the NPA result (36) for $F = 1$; error = 0.1273

Fig. 23

A comparative graph among the numerical evaluation of Eq. (1) and the NPA result (36) for $F = 2$; Error = 0.0808

Fig. 24

A comparative graph among the numerical evaluation of Eq. (1) and the NPA result (36) for $F = 5$; error = 0.054

Fig. 25

A comparative graph among the numerical evaluation of Eq. (35) and the NPA solution (36) for $F = 1$; error = 0.066

Transition Curves and Stability/Instability Zones

In mathematics and physics, a bifurcation is a qualitative shift in a system's behavior when one or more parameters are changed. Bifurcations frequently occur in the field of dynamical systems theory, which examines the temporal evolution of systems under differential equation control. They are essential to comprehend intricate occurrences like phase transitions, chaos, and pattern development [45]. Comprehending bifurcations is essential for forecasting and assessing dynamical system behavior. The study of the beginning of complex patterns and dynamics in a variety of domains, including physics, biology, chemistry, and economics, depends on them. They offer insights into how little changes in parameters may result in significant changes in the system behavior. The current Section examines this phenomenon and the stability regions of the nonlinear Mathieu cubic–quintic DO (9) utilizing the NPA again but using the two independent corresponding solutions:

$$y_{C} (t) = G\cos \omega_{C} t,$$

(41)

and

$$y_{S} (t) = H\sin \omega_{S} t,$$

(42)

where $\omega_{C}$, $\omega_{S}$ are the total frequencies, and $G$, $H$ are the amplitudes of the $\cos -$ frequency and $\sin -$ frequency, respectively.

Now, following the usual NPA as given in Eq. (17), one can get, with the aid of MS, the following two forms:

$$\omega_{C}^{2} = \frac{{ - 4q( - 8 + \pi^{2} \sigma^{2} )\sin (\pi^{2} \sigma )}}{{\pi^{2} \sigma ( - 16 + \pi^{2} \sigma^{2} )}} + a + \frac{3}{4}QG^{2} + \frac{5}{8}RG^{4} ,$$

(43)

and

$$\omega_{S}^{2} = \frac{{32q\sin (\pi^{2} \sigma )}}{{\pi^{4} \sigma^{3} - 16\pi^{2} \sigma }} + a + \frac{3}{4}QH^{2} + \frac{5}{8}RH^{4} .$$

(44)

As previously shown in Floquet theory [46], the transition curves are essential to the stability analysis, so Figs. 26, 27 and 28 are plotted to illustrate the stability configuration in the current case. The frequencies $\omega_{C}$, and $\omega_{S}$ are schemed in these figures against the excitation parameter $q$ as two transition curves to determine the stable and unstable regions in different cases with the data:

Fig. 26

Stability regions for the bifurcation system

Fig. 27

Stability regions with the difference of the normal oscillation $a$

Fig. 28

Stability regions with the difference of the amplitude $G$

$a = 0.5,Q = 0.1,R = 0.1,\sigma = 1.5,\,\,{\text{and}}\,\,G = H = 1$.

Figure 26 indicates that the two curves of $\omega_{C}$, and $\omega_{S}$ intersect at one point at $q = 0$, which is satisfied by the two formulae as given in Eqs. (43) and (44) when $G = H$. This point is called the resonant point. The stable regions are determined by the areas outside the curves [46], whereas the unstable regions are included between the curves.

Figure 27 illustrates the influence of the normal frequency $a$ on the stability distribution, where the letter “S” indicates the stable region and the letter “U” indicates the unstable one. One can observe that when $a$ increases, from 0.1 to 0.5, the resonant point rises on the $\omega$-axis.

Furthermore, Fig. 28 discusses the influence of the amplitude $G$, which is equal to the amplitude $H$, on the stability configuration. It is also found that the growth of $G$, from 0.5 to 2.0, enhances the resonant point on the $\omega$-axis.

Finally, Fig. 29 illustrates the impact of the constant $\sigma$, which is considered as an alternative to the excitation frequency $\Omega$, on the stability arrangement. It is observed that the intersection point is common in all of the transition curves when $\sigma$ rises from 1.2 to 1.5, and the resonant point is constant on the $\omega$-axis.

Fig. 29

Stability regions with the difference of the constant $\sigma$

Conclusions

In this work, the efficiency of the NPA has been adopted to analyze the parametric nonlinear oscillatory structure. The basic dynamical system is represented by the damped Mathieu-cubic quintic DO. The present work aims at obtaining the oscillation amplitude of factorial nonlinear subjects. The approximate solutions are derived apart from the series expansion. Consequently, this investigation aims to obtain estimated findings for small amplitude parametric factors without any limitations, thereby departing from traditional perturbation procedures. Additionally, the method has been extended to find precise answers for the nonlinear large oscillation amplitude. Accurately estimating the frequency–amplitude relationship is essential to get subsequent approximations of the solutions of the parametric non-linear frequency. The produced parametric equation has been validated using the MS, and it exhibits an excellent agreement with the original issue. In multiple examples, the stability behavior has been investigated. The method has produced an extremely high numerical accuracy, is appropriate, straightforward to use, and has simple foundations. The current method is suitable as a mathematical instrument for resolving non-linear parametric investigations since it reduces any mathematical complexities. As a conclusion, one can summarize the key points as follows:

• 1. The discussion is considered a comparative study between the nonlinear damped Mathieu–cubic quintic DO and its equivalent forms by NPA in several cases.

• 2. The convergence between the NPA and the numerical solution of the un-damped Mathieu–cubic quintic DO rises, starting from the special case $\Omega = \omega$ to the general case $\Omega = \sigma /T$, and ending with the enhanced NPA.

• 3. The stability configuration and some PolarPlots have been studied and discussed in the above cases.

• 4. With the existence of the damping term, the conjunction between the NPA and the numerical evaluation of the original formula is found to be enhanced with the rise of the amplitude constant of the equivalent suggested approach.

• 5. The transition curves of the two corresponding solutions, $\cos -$ oscillation and $\sin -$ oscillation, are considered and their conforming stability regions are displayed with the variation of the primary parameters.

• 6. The findings of the obtained results indicate that the approach given here is very straightforward, powerful, premise-based, and quite simple to use. It can be employed for various parameterized issues in the dynamical systems.

• 7. Concerning to the NPA, the following characteristics have been highlighted in relation to the distinctive methodology employed or remarkable outcomes achieved:

  • i. The present nonlinear ODE, with periodic coefficients, is identical to the alternative analogous linear ODE with constant coefficient.

  • ii. The two equations are identical when using the numerical approach.

  • iii. As well-known, Taylor expansion is employed in all conventional methods to mitigate the complexity of similar problems in the presence of restoring forces. The current NPA resolves this weakness.

  • iv. Unlike the other conventional approaches, the NPA allows us to examine the stability analysis of the problem.

  • v. The NPA seems to be a user-friendly, pragmatic, and captivating tool. It can be utilized to analyse many forms of nonlinear oscillators.

  • vi. Furthermore, the NPA is a valuable instrument in the domains of science, technology, and applied research due to its adaptability in addressing diverse nonlinear issues.

• 8. The above points are concerned with the strengths of NPA. Additionally, regarding to potential limitations; it should be noticed that the initial conditions in all previous conditions are the same, and the value of the initial amplitude must be small. Really, the smallness of the absolute error depends mainly on the value initial amplitude.

As a progress works, similar non dynamical system [47, 48] can be analyzed via the NPA.