Skip to main content
SpringerLink
Log in

Numerical Investigation of Broad Mid-Frequency Flexural Bandgap in Composite Sandwich Structures with Periodic Hollow-Shaped Core Geometry

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Objective

Periodic structures have been widely investigated in the past decade because of its potential for noise and vibration reduction. However, there is limited research applying the concept of periodic structures to composite sandwich structures. This paper proposes two lightweight types of periodic hollow-shaped cores in composite sandwich structures, which are simple geometries and able to generate wide flexural bandgap in mid-frequency range for broaden applications.

Methodology

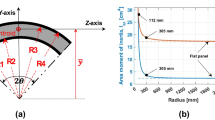
Floquet theory and wave finite element method are used to compute the bandgap behavior. The frequency response function (FRF) of the proposed structures is performed to demonstrate the performance of vibration attenuation by using the finite element simulation.

Results and Conclusions

The FRF shows that the low vibration transmissibility is observed within a certain frequency range, which is consistent with the predicted flexural bandgap. The effect of face–core delamination on the FRF is also examined. Our findings indicate that the proposed structures have higher performance of vibration attenuation than the pristine conventional sandwich structures, even when the proposed structures exhibit face–core delamination. Last, our study demonstrates that despite the simplicity of the core design, it is capable of achieving comparable bandgap behavior to more complex geometries.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Ampatzidis T, Leach RK, Tuck CJ, Chronopoulos D (2018) Band gap behaviour of optimal one-dimensional composite structures with an additive manufactured stiffener, Compos B Eng, vol. 153, pp. 26–35, Nov. https://doi.org/10.1016/j.compositesb.2018.07.012

  2. Valiya Valappil S, Aragón AM, Goosen H (Feb. 2023) Phononic crystals’ band gap manipulation via displacement modes. Solid State Commun 361:115061. https://doi.org/10.1016/j.ssc.2022.115061

  3. Chen Z, Wang G, Shi F, Lim CW (Jun. 2022) Analytical modeling and numerical analysis for tunable topological phase transition of flexural waves in active sandwiched phononic beam systems. Int J Mech Sci 223:107292. https://doi.org/10.1016/j.ijmecsci.2022.107292

  4. Cheng Y, Liu XJ, Wu DJ (2011) Band structures of phononic-crystal plates in the form of a sandwich-layered structure, J Acoust Soc Am, vol. 130, no. 5, pp. 2738–2745, Nov. https://doi.org/10.1121/1.3641365

  5. Guo Z, Sheng M, Pan J (Jul. 2017) Flexural wave attenuation in a sandwich beam with viscoelastic periodic cores. J Sound Vib 400:227–247. https://doi.org/10.1016/j.jsv.2017.04.016

  6. Hussein MI, Hulbert GM, Scott RA (2006) Dispersive elastodynamics of 1D banded materials and structures: analysis, J Sound Vib, vol. 289, no. 4–5, pp. 779–806, Feb. https://doi.org/10.1016/j.jsv.2005.02.030

  7. Hussein MI, Leamy MJ, Ruzzene M (2014) Dynamics of Phononic Materials and Structures: Historical Origins, Recent Progress, and Future Outlook, Appl Mech Rev, vol. 66, no. 4, Jul. https://doi.org/10.1115/1.4026911

  8. Pelat A, Gallot T, Gautier F (Apr. 2019) On the control of the first Bragg band gap in periodic continuously corrugated beam for flexural vibration. J Sound Vib 446:249–262. https://doi.org/10.1016/j.jsv.2019.01.029

  9. Yu K, Chen T, Wang X (May 2013) Band gaps in the low-frequency range based on the two-dimensional phononic crystal plates composed of rubber matrix with periodic steel stubs. Phys B Condens Matter 416:12–16. https://doi.org/10.1016/j.physb.2013.02.011

  10. Zhang Z, Han XK, Ji GM (2018) Mechanism for controlling the band gap and the flat band in three-component phononic crystals, Journal of Physics and Chemistry of Solids, vol. 123, pp. 235–241, Dec. https://doi.org/10.1016/j.jpcs.2018.08.012

  11. Moscatelli M, Ardito R, Driemeier L, Comi C (Aug. 2019) Band-gap structure in two- and three-dimensional cellular locally resonant materials. J Sound Vib 454:73–84. https://doi.org/10.1016/j.jsv.2019.04.027

  12. Mizukami K, Kawaguchi T, Ogi K, Koga Y (Jan. 2021) Three-dimensional printing of locally resonant carbon-fiber composite metastructures for attenuation of broadband vibration. Compos Struct 255:112949. https://doi.org/10.1016/j.compstruct.2020.112949

  13. Ding L, Ding B, Wu Q-Y, Zhu H-P (2023) Flexural Wave Propagation in a Double-Beam System Interconnected by Local Resonators with Two Degrees of Freedom, J Eng Mech, vol. 149, no. 2, Feb. https://doi.org/10.1061/JENMDT.EMENG-6762

  14. An X, Yuan X, Hou X, Fan H (Feb. 2023) Low frequency vibration attenuation of meta-orthogrid sandwich panel with high load-bearing capacity. Compos Struct 305:116560. https://doi.org/10.1016/j.compstruct.2022.116560

  15. Chen JS, Sharma B, Sun CT (2011) Dynamic behaviour of sandwich structure containing spring-mass resonators, Compos Struct, vol. 93, no. 8, pp. 2120–2125, Jul. https://doi.org/10.1016/j.compstruct.2011.02.007

  16. Domadiya PG, Manconi E, Vanali M, Andersen LV, Ricci A (2016) Numerical and experimental investigation of stop-bands in finite and infinite periodic one-dimensional structures, Journal of Vibration and Control, vol. 22, no. 4, pp. 920–931, Mar. https://doi.org/10.1177/1077546314537863

  17. Park S, Jeon W (May 2021) Ultra-wide low-frequency band gap in a tapered phononic beam. J Sound Vib 499:115977. https://doi.org/10.1016/j.jsv.2021.115977

  18. Acar G, Yilmaz C (2013) Experimental and numerical evidence for the existence of wide and deep phononic gaps induced by inertial amplification in two-dimensional solid structures, J Sound Vib, vol. 332, no. 24, pp. 6389–6404, Nov. https://doi.org/10.1016/j.jsv.2013.06.022

  19. Yuksel O, Yilmaz C (Oct. 2015) Shape optimization of phononic band gap structures incorporating inertial amplification mechanisms. J Sound Vib 355:232–245. https://doi.org/10.1016/j.jsv.2015.06.016

  20. Liang Y-J, Dávila CG, Iarve EV (Nov. 2021) A reduced-input cohesive zone model with regularized extended finite element method for fatigue analysis of laminated composites in Abaqus. Compos Struct 275:114494. https://doi.org/10.1016/j.compstruct.2021.114494

  21. Liang Y-J, McQuien JS, Iarve EV (May 2020) Implementation of the regularized extended finite element method in Abaqus framework for fracture modeling in laminated composites. Eng Fract Mech 230:106989. https://doi.org/10.1016/j.engfracmech.2020.106989

  22. Wu K-J, Young W-B (Aug. 2022) Internal characteristics analysis of woven/unidirectional composite angle part by VBO process. Compos Commun 33:101215. https://doi.org/10.1016/j.coco.2022.101215

  23. Wu K-J, Young W-B (2023) Complex angle part fabricated by vacuum bag only process with interleaved dry fiber and prepreg, J Compos Mater, vol. 57, no. 2, pp. 199–211, Jan. https://doi.org/10.1177/00219983221143229

  24. Karsandik Y, Sabuncuoglu B, Yildirim B, Silberschmidt VV (Jun. 2023) Impact behavior of sandwich composites for aviation applications: a review. Compos Struct 314:116941. https://doi.org/10.1016/j.compstruct.2023.116941

  25. Ampatzidis T, Chronopoulos D (Aug. 2019) Mid-frequency band gap performance of sandwich composites with unconventional core geometries. Compos Struct 222:110914. https://doi.org/10.1016/j.compstruct.2019.110914

  26. Kim H-Y, Hwang W (Jan. 2002) Effect of debonding on natural frequencies and frequency response functions of honeycomb sandwich beams. Compos Struct 55(1):51–62. https://doi.org/10.1016/S0263-8223(01)00136-2

  27. Tsai S-N, Taylor AC (Feb. 2019) Vibration behaviours of single/multi-debonded composite sandwich structures with nanoparticle-modified matrices. Compos Struct 210:590–598. https://doi.org/10.1016/j.compstruct.2018.11.071

  28. Mead DJ (1973) A general theory of harmonic wave propagation in linear periodic systems with multiple coupling, J Sound Vib, vol. 27, no. 2, pp. 235–260, Mar. https://doi.org/10.1016/0022-460X(73)90064-3

  29. Phani AS, Woodhouse J, Fleck NA (2006) Wave propagation in two-dimensional periodic lattices, J Acoust Soc Am, vol. 119, no. 4, pp. 1995–2005, Apr. https://doi.org/10.1121/1.2179748

  30. Mace BR, Manconi E (2008) Modelling wave propagation in two-dimensional structures using finite element analysis, J Sound Vib, vol. 318, no. 4–5, pp. 884–902, Dec. https://doi.org/10.1016/j.jsv.2008.04.039

  31. Zhao P, Zhang K, Deng Z (Sep. 2021) Size effects on the band gap of flexural wave propagation in one-dimensional periodic micro-beams. Compos Struct 271:114162. https://doi.org/10.1016/j.compstruct.2021.114162

  32. Liu L, Hussein MI (Jan. 2012) Wave Motion in Periodic Flexural beams and characterization of the transition between Bragg Scattering and local resonance. J Appl Mech 79(1). https://doi.org/10.1115/1.4004592

  33. Jensen JS (Oct. 2003) Phononic band gaps and vibrations in one- and two-dimensional mass–spring structures. J Sound Vib 266(5):1053–1078. https://doi.org/10.1016/S0022-460X(02)01629-2

Download references

Acknowledgements

This work is supported by National Science and Technology Council (NSTC) in Taiwan through the grant MOST 111-2222-E-006 -009 -MY2.

Author information

Authors and Affiliations

  1. Department of Aeronautics and Astronautics, National Cheng Kung University, Tainan, 701, Taiwan

    Te-Han Chu & Yu-Jui Liang

Authors
  1. Te-Han Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu-Jui Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu-Jui Liang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

Supplementary Material 1

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chu, TH., Liang, YJ. Numerical Investigation of Broad Mid-Frequency Flexural Bandgap in Composite Sandwich Structures with Periodic Hollow-Shaped Core Geometry. J. Vib. Eng. Technol. (2024). https://doi.org/10.1007/s42417-024-01420-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42417-024-01420-1

Keywords

Search

Navigation