Skip to main content
SpringerLink
Log in

Finite Element Analysis of Nonlinear Transient Responses of Sandwich Panel with Cut-Out

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

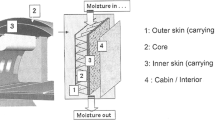
Development of finite element method and higher-order shear deformation based mathematical model of sandwich panel structure with cutout to investigate the nonlinear dynamic responses.

Methods

This work employed a higher-order shear deformation theory and a finite element-based approach to develop the said mathematical model. Geometrical nonlinearity is incorporated using Green–Lagrange’s strains. The dynamic governing equation accounting for geometrical nonlinearity is derived from Hamilton's principle. The nonlinear time-dependent deflection responses are computed utilizing Newmark’s time integration method.

Results

First of all, to check the accuracy of the mathematical model, a comparison study is performed by conducting the comparison between the current numerical and existing literature results. Additionally, the current model is employed to analyze the influence of various parameters such as cutout size, shape, and position, as well as the ratio of core-face thickness and end conditions on the nonlinear dynamic behavior of the sandwich panel with cutout.

Conclusions

Finally, a detailed discussion is presented based on the insights gained from the numerical response analysis. This structured approach ensures a comprehensive understanding of how these factors affect the panel’s behavior under loading conditions, thus contributing valuable information to the field of structural engineering and composite material design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data availability

All the data required are available within the manuscript.

References

  1. Tounsi A, Houari MSA, Benyoucef S, Adda Bedia EA (2013) A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aerosp Sci Technol 24:209–220. https://doi.org/10.1016/j.ast.2011.11.009

    Article  Google Scholar 

  2. Safaei B, Onyibo EC, Goren M, Kotrasova K, Yang Z, Arman S, Asmael M (2023) Free vibration investigation on rve of proposed honeycomb sandwich beam and material selection optimization. Series Mechanical Engineering 21:31–50. https://doi.org/10.22190/FUME220806042S

    Article  Google Scholar 

  3. Safaei B, Moradi-Dastjerdi R, Qin Z, Chu F (2019) Frequency-dependent forced vibration analysis of nanocomposite sandwich plate under thermo-mechanical loads. Compos B Eng 161:44–54. https://doi.org/10.1016/j.compositesb.2018.10.049

    Article  Google Scholar 

  4. Kumar R, Hirwani CK (2022) Investigation on nonlinear bending behavior of sandwich shell panel with cutout using HSDT and FE approach. Mech Based Des Struct Mach 52:1686–1704. https://doi.org/10.1080/15397734.2022.2158868

    Article  Google Scholar 

  5. Reddy JN (1982) Large amplitude flexural vibration of layered composite plates with cutouts. J Sound Vib 83:1–10. https://doi.org/10.1016/S0022-460X(82)80071-0

    Article  Google Scholar 

  6. Alhijazi M, Safaei B, Zeeshan Q, Arman S, Asmael M (2023) Prediction of elastic properties of thermoplastic composites with natural fibers. The Journal of The Textile Institute 114:1488–1496. https://doi.org/10.1080/00405000.2022.2131352

    Article  Google Scholar 

  7. Civalek Ö, Öztürk B, Yavaş A (2007) Nonlinear Transient Dynamic Response of Clamped Rectangular Plates on Two-Parameter Foundations by the Algorithm of the Singular Convolution. International Journal of Science & Technology 2:165–177

    Google Scholar 

  8. Kundu CK, Sinha PK (2006) Nonlinear transient analysis of laminated composite shells. J Reinf Plast Compos 25:1129–1147. https://doi.org/10.1177/0731684406065196

    Article  Google Scholar 

  9. Tornabene F, Fantuzzi N, Bacciocchi M, Dimitri R (2015) Dynamic analysis of thick and thin elliptic shell structures made of laminated composite materials. Compos Struct 133:278–299. https://doi.org/10.1016/j.compstruct.2015.06.052

    Article  Google Scholar 

  10. Wang Z, Yang G, Sun Y, Li Y, Wu F (2023) An improved bare-bones particle swarm algorithm for multi-objective optimization with application to the engineering structures. Facta Universitatis Series: Mechanical Engineering 0:1–23. https://doi.org/10.22190/fume220829004w

    Article  Google Scholar 

  11. Reddy JN (1983) Geometrically nonlinear transient analysis of laminated composite plates. AIAA J 21:621–629. https://doi.org/10.2514/3.8122

    Article  Google Scholar 

  12. Lee SJ, Reddy JN, Rostam-Abadi F (2004) Transient analysis of laminated composite plates with embedded smart-material layers. Finite Elem Anal Des 40:463–483. https://doi.org/10.1016/S0168-874X(03)00073-8

    Article  Google Scholar 

  13. Makhecha DP, Ganapathi M, Patel BP (2001) Dynamic analysis of laminated composite plates subjected to thermal/mechanical loads using an accurate theory. Compos Struct 51:221–236. https://doi.org/10.1016/S0263-8223(00)00133-1

    Article  Google Scholar 

  14. Nanda N, Bandyopadhyay JN (2009) Geometrically nonlinear transient analysis of laminated composite shells using the finite element method. J Sound Vib 325:174–185. https://doi.org/10.1016/j.jsv.2009.02.044

    Article  Google Scholar 

  15. Lee WH, Han SC, Yoon SH (1998) Transient analysis of partially supported laminated composite plates with cut-outs. J Korean Society Steel Const 10:667–676

    Google Scholar 

  16. Nayak CB, Khante SN (2021) Linear Transient Dynamic Analysis of Plates With and Without Cutout. Arab J Sci Eng 46:10681–10693. https://doi.org/10.1007/s13369-021-05523-9

    Article  Google Scholar 

  17. Lee SY, Hwang JG (2019) Finite element nonlinear transient modelling of carbon nanotubes reinforced fiber/polymer composite spherical shells with a cutout. Nanotechnol Rev 8:444–451. https://doi.org/10.1515/ntrev-2019-0039

    Article  Google Scholar 

  18. Chen J, Dawe DJ, Wang S (2000) Nonlinear transient analysis of rectangular composite laminated plates. Compos Struct 49:129–139. https://doi.org/10.1016/S0263-8223(99)00108-7

    Article  Google Scholar 

  19. Malekzadeh P, Fiouz AR, Razi H (2009) Three-dimensional dynamic analysis of laminated composite plates subjected to moving load. Compos Struct 90:105–114. https://doi.org/10.1016/j.compstruct.2009.02.008

    Article  Google Scholar 

  20. Botshekanan Dehkordi M, Khalili SMR, Carrera E (2016) Non-linear transient dynamic analysis of sandwich plate with composite face-sheets embedded with shape memory alloy wires and flexible core- based on the mixed LW (layer-wise)/ESL (equivalent single layer) models. Compos B Eng 87:59–74. https://doi.org/10.1016/j.compositesb.2015.10.008

    Article  Google Scholar 

  21. Karakoti A, Pandey S, Kar VR (2022) Nonlinear transient analysis of porous P-FGM and S-FGM sandwich plates and shell panels under blast loading and thermal environment. Thin-Walled Structures 173:108985. https://doi.org/10.1016/j.tws.2022.108985

    Article  Google Scholar 

  22. Burlayenko VN, Sadowski T (2012) Finite element nonlinear dynamic analysis of sandwich plates with partially detached facesheet and core. Finite Elem Anal Des 62:49–64. https://doi.org/10.1016/j.finel.2012.08.003

    Article  MathSciNet  Google Scholar 

  23. Zhang J, Zhu X, Yang X, Zhang W (2019) Transient nonlinear responses of an auxetic honeycomb sandwich plate under impact loads. Int J Impact Eng 134:103383. https://doi.org/10.1016/j.ijimpeng.2019.103383

    Article  Google Scholar 

  24. Burlayenko VN, Sadowski T (2014) Transient dynamic response of debonded sandwich plates predicted with finite element analysis. Meccanica 49:2617–2633. https://doi.org/10.1007/s11012-014-9924-y

    Article  MathSciNet  Google Scholar 

  25. Bui TQ, Khosravifard A, Zhang C, Hematiyan MR, Golub MV (2013) Dynamic analysis of sandwich beams with functionally graded core using a truly meshfree radial point interpolation method. Eng Struct 47:90–104. https://doi.org/10.1016/j.engstruct.2012.03.041

    Article  Google Scholar 

  26. Roque CMC, Ferreira AJM, Neves AMA, Soares CMM, Reddy JN, Jorge RMN (2011) Transient analysis of composite and sandwich plates by radial basis functions*. J Sandwich Struct Mater 13:681–704. https://doi.org/10.1177/1099636211419132

    Article  Google Scholar 

  27. Upadhyay AK, Shukla KK (2013) Non-linear static and dynamic analysis of skew sandwich plates. Compos Struct 105:141–148. https://doi.org/10.1016/j.compstruct.2013.05.007

    Article  Google Scholar 

  28. Nath Y, Shukla KK (2001) Non-linear transient analysis of moderately thick laminated composite plates. J Sound Vib 247:509–526. https://doi.org/10.1006/jsvi.2001.3752

    Article  Google Scholar 

  29. Reddy JN (2004) Mechanics of Laminated Composite Plates and Shells Theory and Analysis. CRC Press, New York

    Google Scholar 

  30. Hari Kishore MDV, Singh BN, Pandit MK (2011) Nonlinear static analysis of smart laminated composite plate. Aerosp Sci Technol 15:224–235. https://doi.org/10.1016/j.ast.2011.01.003

    Article  Google Scholar 

  31. Elmoghazy YH, Safaei B, Sahmani S (2023) Finite element analysis for dynamic response of viscoelastic sandwiched structures integrated with aluminum sheets. Facta Universitatis, Series: Mechanical Engineering 21:591. https://doi.org/10.22190/fume231004045e

    Article  Google Scholar 

  32. Cook RD, Malkus DS, Plesha ME (2000) Concepts and Applications of Finite Element Analysis. Willey, New York

    Google Scholar 

  33. Bathe K-J, Ramm E, Wilson EL (1975) Finite element formulations for large deformation dynamic analysis. Int J Numer Methods Eng 9:353–386. https://doi.org/10.1002/nme.1620090207

    Article  Google Scholar 

  34. Kumar R, Tiwari S, Kumar Hirwani C (2023) On transient responses of sandwich plate with cutout using FEM. Mater Today Proc. https://doi.org/10.1016/j.matpr.2023.05.409

    Article  Google Scholar 

  35. Marjanović M, Vuksanović D (2013) Linear Transient Analysis of Laminated Composite Plates using GLPT. Acta Technica Napocensis: Civil Engineering & Architecture 56:58–71

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology Patna, Bihar, 800005, India

    Ravi Kumar & Chetan Kumar Hirwani

Authors
  1. Ravi Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chetan Kumar Hirwani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chetan Kumar Hirwani.

Ethics declarations

Conflict of interest

All authors have no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, R., Hirwani, C.K. Finite Element Analysis of Nonlinear Transient Responses of Sandwich Panel with Cut-Out. J. Vib. Eng. Technol. (2024). https://doi.org/10.1007/s42417-024-01407-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42417-024-01407-y

Keywords

Search

Navigation