Vibrations of a Bridge with Random Structural Irregularities Under Random Traffic Load and a Probabilistic Structural Degradation Assessment Approach

Abstract

Purpose

Dynamic loads like traffic make bridges vibrate. Especially for bridges with a large span, vibrations have a significant impact on their structural stability and durability. Due to material defects, fatigue and other influences, a bridge typically has random structural irregularities, which affect its dynamic response. In this work, an effective mathematical approach is presented to study the dynamic response of a model single span slender beam bridge, in the presence of random structural irregularities. In addition, an approach to assess the structural degradation of a bridge is presented.

Methods

The slender beam bridge is modelled as an Euler-Bernoulli beam and the random structural irregularities are considered by random fields in the bending stiffness and the mass per unit length. As an illustrative example, the vibrations of a model road bridge are investigated for randomly crossing vehicles. After Monte Carlo experiments with and without random structural irregularities the vibrations and mechanical stresses of the bridge are determined and analysed.

Results

The study shows statistically significant variations in the most dominant frequencies with and without random structural irregularities.

Conclusion

The influence of the random irregularities on the structural stability status of a bridge may not be negligible. The probability of a serious structural degradation in the bridge can be assessed by means of a binomial logistic model. The developed approach enables a better understanding of the vibrations and structural status of bridges, taking into account random structural irregularities and random traffic.

Introduction

A bridge is a structure that spans a physical obstacle to make it easier to cross. An engineer’s job is to ensure the structural stability of a bridge and its durability with minimal maintenance. While a bridge’s response to the applied loads is well understood, the applied traffic loads are still the subject of research [40]. Traffic loads are dynamic loads and cause a bridge to vibrate. Especially for bridges with a large span, vibrations contribute to the stresses and have a significant impact on structural and material fatigue.

Vibration monitoring of a bridge is a useful and widespread technique for assessing the current condition of a bridge, in which damages or structural degradation can be detected, for example, by changes in the natural frequencies or in the frequency spectrum of the response due to ambient excitation.

A further issue is the presence of random material and structural irregularities. For example, beam bridges for road traffic are often made of reinforced concrete. Reinforced concrete is an inexpensive material in which reinforcing bars (rebars, e.g. made of steel) are usually embedded in concrete before the concrete sets. Due to material defects, influences during the construction process or material fatigue (e.g. cracks), a bridge made of reinforced concrete typically exhibits random irregularities [1].

The influence of the system’s response due to random structural irregularities in reinforced concrete have been investigated in static load settings for beams and columns in [44]. According to our literature search, such random structural irregularities were not yet taken into account in the existing investigations about the dynamic behaviour of bridges.

It is the purpose of this paper to combine the dynamic analysis of traffic induced vibrations with the effects arising from random material irregularities. This is a methodological study. It is based on a model slender single span beam bridge for road traffic. It will be shown that the presence of random structural irregularities changes the frequency spectrum of the response in a statistically significant way. Therefore, random imperfections of a bridge cannot be neglected in a probabilistic safety assessment. Apart from enabling a better understanding of bridge vibrations, the presented methodology allows one to predict the probability of serious structural degradation, based on changes of the most dominant frequency in the system response, conditional on knowledge of the bending stiffness curve.

There is a vast literature on vibration based condition monitoring. Standard methods have been reviewed in the paper [7], while [15] compare frequency-based methods with mode shape-based methods. Indirect bridge monitoring using passing vehicles is addressed in [34]. A comparative numerical and experimental study using forced and ambient vibrations can be found in [16]; a further case study of damage identification based on mode shape properties is given in [33], while [42] compare a larger number of modal techniques; both latter references use the Z24 bridge in Switzerland as the object of study. A more recent survey of damage identification methods for bridges is in [2], separating beam-, truss-, arch- and suspension bridges.

The dynamic response of beams that are subjected to moving loads has been studied extensively for railway tracks and bridges. The monograph [17] is a basic reference, while the monograph [53] is referred to for modelling random track irregularities, in addition. Especially the effects of high-speed trains have aroused interest; what concerns the induced soil-structure interaction, see [10]; for failure probabilities depending on track irregularities, ballast temperature and train velocity, see [24] and references therein.

Pioneering work on vibrations of structures under moving loads was done by [18], especially on beams and plates. One research direction concerns crack development in concrete structures [32] and crack detection in beams using a moving sensor method [30]. Another research direction addresses the dynamics of beams with viscoelastic [43] or nonlinear [26] boundary conditions. Further research concerns damping effects due to vehicle-bridge interaction [49], FE-modelling of bridge-vehicle interaction under stochastic road profile [21], or extracting bridge frequencies by observing the response of a passing vehicle [52]. Some of the references, such as [21] or [49], use sophisticated finite element models for studying the vehicle-bridge interaction; however, such models are computationally expensive. Therefore, the approach using moving loads on an Euler-Bernoulli beam is still frequently used for theoretical preliminary investigations of slender bridges.

Road traffic on a bridge is highly variable and usually a random process. For basic concepts, see [40, Section 2.3]. A review of statistical methods for load effects on bridges is given in [39], with emphasis on statistical headway models in [38]. For a survey of deterministic and stochastic traffic flow models, see [25]. For congestion models, car-following and lane-changing models, or more generally, intelligent-driver models, see [6]. For bridge-vehicle interaction models and random traffic generated by a cellular automaton, see [29]. Moving forces driven by an Erlang renewal process are employed in [28], while a compound Poisson process involving random loads with a continuous distribution is proposed in [20].

In this work, an effective mathematical approach of low computational cost is presented to study the dynamic response of a single span slender beam bridge (simply supported), in which its random structural irregularities are taken into account. The slender beam bridge is modelled as an Euler-Bernoulli beam and the random structural irregularities are introduced by considering the bending stiffness and the mass per unit length as Gaussian random fields. The random traffic load consists of different types of vehicles passing the bridge in random order, with random speeds, random masses and random distances between two consecutive vehicles.

Monte Carlo experiments are a useful numerical approach for investigating the response of a system under random input [13]. In this paper, Monte Carlo simulations are performed with and without random structural irregularities. The vibrations and bending stresses of the bridge under random traffic loads are determined and statistically analysed. In addition, a machine learning approach (a binomial logistic model) is formulated to assess the probability of a serious structural degradation in the bridge.

The main findings of the paper consist in a new Monte Carlo based methodology for assessing the joint effects of random traffic and random material irregularities. It is seen that the random material irregularities induce a change in the dominant frequency of the response of the system, which is proven to be statistically highly significant. Based on this observation, a method for predicting the probability of serious degradation is proposed. The latter application requires knowledge of the bending stiffness curve, which is a model input in this paper, but can be obtained efficiently from static deflection data [12].

A short explanation of the applied stochastic formulation of the beam’s random irregularities is in order. The random fields for the bending moment and the mass per unit length, respectively, are modelled as the sum of a deterministic mean field, which may depend on the longitudinal coordinate x, and a mean-zero stationary Gaussian random field. The random fields are characterized by their variances and correlation lengths, entered in an exponential autocorrelation function. These statistical hypotheses will be discussed and justified at the end of Section 4. In the numerical experiments of the present paper, the mean fields are taken constant for computational simplicity. In particular, the cross section is constant, that is, the beam is prismatic. However, the method applies equally well to beams with deterministic mean fields depending on the longitudinal variable x. Considering the mean field as a function of x could accommodate recent research on functionally graded, nonuniform beams as in [41] or [46]. At the expense of a more elaborate beam model, tapered beams as in [45] could be supplemented by a stochastic model, as well as the axially loaded beam-spring system that was designed for vibration control in [51].

The plan of the paper is as follows. Section 2 is devoted to the employed methods. It introduces the bridge model, the stochastic models of the structural irregularities as well as the traffic. The numerical solution technique is briefly described, with details shifted to the Appendix. Concepts of Monte Carlo simulation are mentioned. Finally, the statistical method for estimating the probability of serious structural degradation is presented. Section 3 contains the description of the data and the results of the Monte Carlo simulations with random traffic and with/without random structural irregularities. A discussion of the results is given in Section 4, while Section 5 is dedicated to the conclusions as well as an outlook for future research and applications.

Methods

Bridge Model

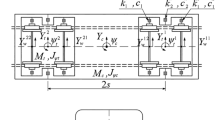
In this work we are focusing on a single span slender beam bridge. The time-dependent vertical deflections w(x, t) of a slender bridge are modelled as a damped Euler-Bernoulli beam of length L. Its vibrations are described by the equation of motion, see [14]

$$\begin{aligned}&\left( EI(x)w_{xx}\right) _{xx}+\rho A(x)w_{tt}\nonumber \\&\quad +\beta \left( EI(x)(w_t)_{xx}\right) _{xx}+\alpha \rho A(x)w_t=f(x,t). \end{aligned}$$

(1)

Here, x denotes the longitudinal coordinate, t the time, EI(x) the bending stiffness, $\rho A(x)$ the mass per unit length of the bridge, and f the line loads acting on the bridge (e.g. traffic). The bending stiffness EI(x) is the product of the elastic modulus E(x) and the moment of inertia I(x) of the bridge. The mass per unit length $\rho A(x)$ is the product of the mass density $\rho (x)$ and the the cross sectional area A(x) of the bridge. The coefficients $\beta$ and $\alpha$ stand for the internal and external damping coefficients. The lower indices $_x$ and $_t$ represent the derivatives with respect to x and t, respectively. The sub-index $_{xx}$ represents e.g. the second derivative with respect to x.

In this study a simply supported beam bridge is examined (see Fig. 1). The boundary conditions are given as follows:

$$\begin{aligned}&w(0,t)=0 ,\quad w_{xx}(x,t){\Big \vert }_{x=0}=0 \end{aligned}$$

(2)

$$\begin{aligned}&w(L,t)=0 ,\quad w_{xx}(x,t){\Big \vert }_{x=L}=0 \end{aligned}$$

(3)

Since the bridge is assumed to be at rest at $t=0$ the initial deflection and deflection speed are set to zero:

$$\begin{aligned}&w(x,0)=0 ,\quad w_t(x,t){\Big \vert }_{t=0}=0. \end{aligned}$$

(4)

Fig. 1

Bridge model: dynamics of a simply supported slender beam bridge, modelled as an Euler–Bernoulli beam (grey line)

Structural Irregularities

The random structural irregularities of a bridge are taken into account in the beam equation (1) by adding random fields. Random fields $r_{EI}(x)$ and $r_{\rho A}(x)$ are added to a mean bending stiffness $EI_0(x)$ and a mean mass per unit length $\rho A_0(x)$

$$\begin{aligned}&EI(x) = EI_0(x)+r_{EI}(x) \end{aligned}$$

(5)

$$\begin{aligned}&\rho A(x) = \rho A_0(x) + r_{\rho A}(x) \end{aligned}$$

(6)

A random field assigns a random variable at every point x. The random fields $r_{EI}(x)$ and $r_{\rho A}(x)$ are assumed Gaussian and stationary. Thus, they are completely specified by the constant mean value

$$\begin{aligned}&\mu _{r_{EI}} = {\mathbb {E}}(r_{EI}(x))= 0 \end{aligned}$$

(7)

$$\begin{aligned}&\mu _{r_{\rho A}} = {\mathbb {E}}(r_{\rho A}(x))= 0 , \end{aligned}$$

(8)

the field variance ($\sigma _{EI}^2$ and $\sigma _{\rho A}^2$) and an autocorrelation function

$$\begin{aligned}&c_{EI}(\Delta )=c_{EI}(x-{\hat{x}})\end{aligned}$$

(9)

$$\begin{aligned}&c_{\rho A}(\Delta )=c_{\rho A}(x-{\hat{x}}) \end{aligned}$$

(10)

for any two points x and ${\hat{x}}$ at distance $\Delta$, see [37]. We take for both random fields the autocorrelation function in the form of

$$\begin{aligned}&c_{\star }(\Delta )=\text {e}^{-\vert \Delta \vert /l_{\star }} \end{aligned}$$

(11)

with the so-called correlation length $l_{\star }$, see [11]. The symbol $\star$ is just a placeholder for EI and $\rho A$.

The standard method for simulating a random field $r_\star (x)$ is based on the Karhunen-Loève expansion [5]. It is obtained by solving the eigenvalue problem

$$\begin{aligned}&\sigma _\star ^2 \int \limits _0^L c_\star (x-{\hat{x}})\varphi _{\star ,k}({\hat{x}})\text {d}{\hat{x}}=\lambda _{\star ,k}\varphi _{\star ,k}(x). \end{aligned}$$

(12)

This eigenvalue problem results in a Fredholm integral equation of the second kind. It yields a sequence of positive eigenvalues $\lambda _{\star ,k}$ and orthonormal eigenfunctions $\varphi _{\star ,k}(x)$ [19]. Then the random field can be represented as

$$\begin{aligned}&r_\star (x)=\sum _{k=1}^{\infty }\sqrt{\lambda _{\star ,k}}\xi _{\star ,k} \varphi _{\star ,k}(x) \end{aligned}$$

(13)

where the $\xi _{\star ,k}$ are uncorrelated random variables with unit variance. If the process is Gaussian, the $\xi _{\star ,k}$ are independent and distributed according to the standard normal distribution ${\mathcal {N}}(0,1)$. Figure 2 shows the mean bending stiffness $EI_0(x)$ (black dashed line) and a realization of the random bending stiffness EI(x) (grey line). The plausibility of the local maximum variations in the realizations is explained in the discussion section (Section 4). Figure 3 shows the mean mass per unit length $\rho A_0(x)$ (black dashed line) and a realization of the random mass per unit length $\rho A(x)$ (grey line).

For the sake of simplicity, it is assumed in this work that the cross-section of the bridge is constant for all simulations (i.e. a prismatic beam). This means that not the bending stiffness EI(x) and the mass per unit length $\rho A(x)$ are generated as random fields, but rather the elastic modulus E(x) and the density $\rho (x)$. Because of the different orders of magnitude, small error rates of the modulus of elasticity E(x) and the density $\rho (x)$ are much more decisive than small error rates of the the geometric parameters for the bending stiffness EI(x) and the mass per unit length $\rho A(x)$, this assumption has no major impact on the generation of the random fields. A prismatic beam with random non-homogeneous material behavior is thus examined.

Fig. 2

Mean bending stiffness $EI_0(x)$ (black dashed line) and a realization of the random bending stiffness EI(x) (grey line)

Fig. 3

Mean mass per unit length $\rho A_0(x)$ (black dashed line) and a realization of the random mass per unit length $\rho A(x)$ (grey line)

Random Traffic

The vehicles that cross the bridge are modelled as randomly moving point masses. In this study, different types of vehicles are taken into account. Since heavy vehicles are more interesting for the load on the bridge than light ones, four different types of trucks are considered (see Table 1). These four different types of trucks pass the bridge in random order with random speeds, random masses and random distances between two consecutive trucks. The random moving point masses act as point loads on the bridge and are taken into account in the partial differential Eq. (1) in the line load

$$\begin{aligned} f(x,t)=&\sum _{i=1}^{N_a}P_i\delta (x-(v_it-s_i))[\sigma (v_it-s_i)\nonumber \\&-\sigma (v_it-(s_i+L))] \end{aligned}$$

(14)

Here, $N_a$ is the number of moving axles, $\delta (x)$ is the Dirac delta distribution and $\sigma (x)$ the Heaviside step function. The value $P_i$ is the axial load and $v_i$ the velocity of the vehicle axle i. The value $s_i$ is the distance of the axle i to the origin ($x=0$) in the entire vehicle convoy at time $t=0$ and is given by the sum of the previous axle distances $d_k$

$$\begin{aligned}&s_i = \sum _{k=1}^{i} d_k \quad \text {for } i = 1,...,N_a. \end{aligned}$$

(15)

Here, $d_k$ is the spatial distance between the axle $k-1$ and k. The value $d_1$ is the distance to the beginning of the bridge that the very first axle has at time $t=0$. The values $P_i$, $v_i$ and $d_k$ are supposed to be random values with certain restrictions described below.

The axial load $P_i$ is assumed to be random. The distribution depends on the type of vehicle and is different for each axle. While the axle loads are normally distributed for smaller vehicles (e.g. cars, vans), it looks different for large and heavy trucks. In particular, the distribution of the axle loads under the lorry bed depends on the cargo and is somewhat more complex (cf. Fig. 4). However, this distribution can be modelled as a Gaussian mixture model [3].

Fig. 4

Distribution of the axle loads of vehicle type 2: Normal distribution under the driver’s cab and a Gaussian mixture model under the lorry bed

The random value of the velocities $v_i$ is assumed to be normally distributed and the velocity for the axles within a vehicle remains constant during the entire bridge crossing. We assume the same distribution for all four vehicle types with mean value $v_0$ = 20 m/s and standard deviation $\sigma = 2$ m/s.

The spatial distance $d_i$ between the axle within the vehicle is constant and is given according to the type of vehicle. The random distance $d_i$ between two consecutive vehicles is given as

$$\begin{aligned} d_i = \Delta _i v_i \end{aligned}$$

(16)

where the time distance $\Delta _i$ between the two consecutive vehicles is assumed to be exponentially distributed with $\lambda = 60/16$ (i.e. 16 trucks cross the bridge on average in one minute) and is generated at $t=0$.

Since the traffic flow is a random process, overtaking manoeuvres are basically possible. A multi-lane bridge is therefore assumed for the simulation.

The random order of the vehicles is generated based on a discrete probability distribution $p_j$ for the four different vehicle types, which are taken from the literature [3] (see Table 1).

Table 1 Types of vehicles including number of axles and probability of occurrence $p_j$

Solution Method

In the following, we describe the solution of the differential Eq. (1) with a single realisation of the random bending stiffness EI(x). The differential Eq. (1) is solved by the spectral method [36]. The spectral method is a numerical technique for solving a class of partial differential equations. The idea of this method is to write the solution of the differential equation as a linear combination of appropriate basis functions that satisfy the differential equation as accurately as possible. In the case of time-dependent partial differential equations on a spatial domain, the appropriate basis functions are usually chosen for the spatial variables x and are defined so that the boundary conditions are fulfilled. The linear coefficients are time-dependent. Here, the appropriate basis functions $\varphi _k(x)$ are chosen as the normal modes of a homogeneous simply supported beam, so that the boundary conditions (2) are fulfilled (see [22]):

$$\begin{aligned} \varphi _k(x)=\sin \left( \frac{k\pi x}{L}\right) . \end{aligned}$$

(17)

After applying the spectral method to Eq. (1) (see Appendix A) we finally get the system of linear ordinary differential equations (ODE) of second order

$$\begin{aligned}&{\mathbf {M}} \cdot {\mathbf {{b}}}(t)_{tt}+\left( \beta {\mathbf {K}} +\alpha {\mathbf {M}} \right) \cdot \mathbf {{b}}(t)_{t} + {\mathbf {K}} \cdot {\mathbf {b}}(t)= {\mathbf {f}}(t) \end{aligned}$$

(18)

with mass matrix ${\mathbf {M}}$, matrix ${\mathbf {K}}$ and vector ${\mathbf {f}}(t)$ with entries ${\mathbf {M}}_{lk}$, ${\mathbf {K}}_{lk}$ and ${\mathbf {f}}_{l}(t)$ for $l = 1,...,N$ and $k = 1,...,N$. The resulting integrals in the entries are determined numerically with an adaptive quadrature [47].

Since the matrix ${\mathbf {M}}$ is regular, we can formulate the Eq. (18) as follows:

$$\begin{aligned} {\mathbf {b}}(t)_{tt}= -{\mathbf {M}}^{-1}\cdot {\mathbf {K}} \cdot {\mathbf {b}}(t)-(\beta \cdot {\mathbf {M}}^{-1}\cdot {\mathbf {K}} +\alpha \cdot {\mathbf {I}} )\cdot {\mathbf {b}}(t)_{t} \end{aligned}$$

(19)

where ${\mathbf {I}}$ is the identity matrix. Using the velocity components ${\mathbf {d}}(t)={\mathbf {b}}(t)_{t}$, we can rewrite the system of linear ordinary differential equations of second order (19) into a system of ordinary differential equation of first order:

$$\begin{aligned} {\mathbf {b}}(t)_{t}&={\mathbf {d}}(t)\nonumber \\ {\mathbf {d}}(t)_{t}&= -{\mathbf {M}}^{-1}\cdot {\mathbf {K}} \cdot {\mathbf {b}}(t)-(\beta \cdot {\mathbf {M}}^{-1}\cdot {\mathbf {K}} +\alpha \cdot {\mathbf {I}} )\cdot {\mathbf {d}}(t). \end{aligned}$$

(20)

This system can be written as a matrix differential equation of first order

$$\begin{aligned} \begin{pmatrix} {\mathbf {b}}(t)\\ {\mathbf {d}}(t) \end{pmatrix}_t = \begin{pmatrix} 0&{}{\mathbf {I}} \\ -{\mathbf {M}}^{-1}\cdot {\mathbf {K}} &{} -\beta \cdot {\mathbf {M}}^{-1}\cdot {\mathbf {K}} -\alpha \cdot {\mathbf {I}} \end{pmatrix} \cdot \begin{pmatrix} {\mathbf {b}}(t)\\ {\mathbf {d}}(t) \end{pmatrix} \end{aligned}$$

(21)

with initial coefficient ${\mathbf {b}}(0)$, which resulted from the initial bending and ${\mathbf {d}}(0)=0$, which resulted from the initial velocity (the bridge is at rest at the beginning). The matrix differential Eq. (21) is typically a stiff ordinary differential equation and is solved numerically in Matlab using a standard solver for stiff ordinary differential equations with step size control (ode23s, which is an embedded method using two linearly implicit Runge-Kutta methods of order 2 and 3 for the error estimation, for more details see [23, 48]).

Monte Carlo Experiments and Data Analysis

The simulation model is computed repeatedly with randomly generated inputs for the bending stiffness EI(x), mass per unit length $\rho A(x)$ and the traffic, as explained above (first Monte Carlo experiment). The system’s responses are determined for the time range $0<t<30$ sec and statistically analysed.

The mean values and standard deviations are calculated for the most dominant frequencies of the deflection and the acceleration in the middle of the bridge at $x = L/2$. The dominant frequencies of the system responses are determined by an amplitude spectrum using a fast Fourier transform (FFT). The most dominant frequency is identified as the frequency at which the maximum of the amplitude spectrum occurs. The distribution of the most dominant frequencies in all simulations is graphically represented by a histogram. The mean and the standard deviation of the sample are also calculated.

To determine the influence of the random fields in the bending stiffness and the mass per unit length on the system response, a second Monte Carlo experiment is carried out in which the bending stiffness and the mass per unit length are chosen as constant (prismatic homogeneous beam, $EI_0$ and $\rho A_0$ constant, without random fields) and only the traffic is generated randomly. Then, the most dominant frequencies of the vibration in the middle of the bridge ($x = L/2$) are compared graphically (with a histogram) and statistically (with a two sample t-test for the mean values) for the two Monte Carlo experiments (with and without random fields). For a two sample t-test, there is a statistically significant difference between the mean values of two samples with an error probability of $\alpha \, \%$, when the p-value is less than $\frac{\alpha }{100}$ (i.e., $p<\frac{\alpha }{100}$). Typical error probabilities are 5% or 1% but in practice the p-value is usually much smaller when the mean values are different (see [35]).

Structural Degradation Assessment

Frequency analysis of the bridge vibrations is a frequently used tool for assessing the current condition of a bridge. Damages or structural degradation in bridges can be detected by frequency changes [7, 15]. If the dominant frequencies $F_{\text {dom}}$ fall below a certain value $F_{\text {crit}}$, the bridge is classified as defective. The question always arises as to where this limit frequency $F_{\text {crit}}$ is set. Here, the limit of the most dominant frequency in the system response for the identification of serious structural degradation is set to the minimum of the most dominant frequency in the system response that resulted in the second Monte Carlo experiment (without random fields). We used a (binomial) logistic model to assess the probability of a serious structural degradation ($Y=1$) in the bridge based on its bending stiffness. This model is given as [9]

$$\begin{aligned} P(Y=1\vert X=\eta )=\frac{e^{\beta _1+\beta _2 \eta }}{1+e^{\beta _1+\beta _2 \eta }} \end{aligned}$$

(22)

where the predictor $\eta$ is defined as

$$\begin{aligned} \eta = \int \limits _{0}^{L} \left| \min \left\{ 0,EI(x)-EI_0 \right\} \right| \, \text {d}x. \end{aligned}$$

(23)

This predictor $\eta$ measures the area of the bending stiffness curve EI(x) that is below the mean bending stiffness $EI_0$ (see grey area in Fig. 5). The regression coefficients $\beta _1$ and $\beta _2$ are determined based on the results of the first Monte Carlo experiment (with the random fields). The goodness of fit is measured by the pseudo-R-squared value [8]:

$$\begin{aligned}&R^2_L=\frac{D_{\text {null}}-D_{\text {fitted}}}{D_{\text {null}}} \end{aligned}$$

(24)

where $D_{\text {null}}$ is the null deviance, which represents the difference between a model with only the intercept (“no predictors”) and the saturated model, and $D_{\text {fitted}}$ is the deviance of the model (22), which represents the difference between the model (22) and the saturated model.

Fig. 5

Mean bending stiffness $EI_0(x)$ (black dashed line), a realization of a random bending stiffness EI(x) (grey line) and the predictor $\eta$ (grey area)

The maximum bending stress in the bridge is calculated for each simulation as

$$\begin{aligned}&\sigma _{\text {max}}= \max _{x,t} \left| d_{\bot }(x)E(x)w_{xx}(x,t)\right| \end{aligned}$$

(25)

Here, it is assumed that the maximal bending stress occurs at the top or bottom of the bridge cross section. Thus, the function $d_{\bot }(x)$ is given by the larger normal distance from the neutral axis to the top or bottom of the bridge at the position x, which depends on the geometry of the cross section. The distributions of the positions at which the maximum bending stress occurs are shown graphically in histograms for both Monte Carlo experiments. The values of the maximum bending stresses and the positions at which they occur are also analysed.

Procedure for degradation assessment in brief:

• 1. Model the bridge to be examined using the Euler–Bernoulli beam Eq. (1) with the bending stiffness $EI_0(x)$ and mass per unit length $\rho A_0(x)$ of the intact state (initial state) of the bridge

• 2. Generate N plausible random traffic flows $f_i(x,t)$ (for $i = 1,...,N$) that will pass the bridge

• 3. Run Monte Carlo simulations with the generated random traffic $f_i(x,t)$ for $i=1,...,N$ for the intact bridge ($EI_0(x)$ and $\rho A_0(x)$), calculate the most dominant frequency $F_{\text {dom},i}$ in each realization i and determine the minimum of the most dominant frequency (limit frequency)

  $$\begin{aligned}F_{\text {crit}}= \min _{1\le i \le N} F_{\text {dom},i} \end{aligned}$$

• 4. Generate N different structural irregularities in the bending stiffness $EI_i(x)$ and mass per unit length $\rho A_i(x)$ by adding random fields $r_{EI,i}(x)$ and $r_{\rho A,i}(x)$ to the initial bending stiffness $EI_0(x)$ and mass mass per unit length $\rho A_0(x)$ (for $i=1,...,N$):

  $$\begin{aligned}&EI_i(x) = EI_0(x)+r_{EI,i}(x) \\&\rho A_i(x) = \rho A_0(x) + r_{\rho A,i}(x) \end{aligned}$$

• 5. Perform Monte Carlo simulations with the same generated random traffic flows as above $f_i(x,t)$ and the structural random irregularities ($EI_i(x)$ and $\rho A_i(x)$) for $i = 1,...,N$, calculate the most dominant frequency $F_{\text {dom},i}^{\text {random}}$ in each realization i and classify the simulation as defective or intact based on the limit frequency $F_{\text {crit}}$. The bridge resulting from realization i is classified as defective if

  $$\begin{aligned}F_{\text {dom},i}^{\text {random}}<F_{\text {crit}}. \end{aligned}$$

• 6. Generate the defective versus intact logistic regression model with respect to the predictor $\eta$:

  $$\begin{aligned} P(Y=1\vert X=\eta )=\frac{e^{\beta _1+\beta _2 \eta }}{1+e^{\beta _1+\beta _2 \eta }}. \end{aligned}$$

• 7. Determine the bending stiffness of the real bridge (see [12] and literature therein) and estimate the probability of degradation using the logistic regression model ${P(Y=1\vert X=\eta )}$.

Results

In the first Monte Carlo experiment, N=400 simulations were calculated in which the bending stiffness, mass per unit length and the traffic were randomly generated as described in the section above. The mean bending stiffness $EI_0$ is set to $1.5 \times 10^{10}$ [$\hbox {Nm}^2$], the mean mass per unit length $\rho A_0$ to 15000 [kg/m] and the length L to 10 [m] (see Figs. 2 and 3). The parameters for the random fields are fictitious but motivated by the range of values reported in the literature [4, 27, 50] and are taken as follows: the correlation lengths $l_{EI}=l_{\rho A}=1$ [m] and for the field standard deviations $\sigma _{EI}=EI_0/10$ (i.e. 10$\%$ of $EI_0$) and $\sigma _{\rho A}=\rho A_0/50$ (i.e. 2$\%$ of $\rho A_0$) (see also Table 2). The cross-section of the bridge is assumed to be rectangular with a width of $b(x)=6$ [m] and a thickness of $h(x)=1$ [m]. The damping coefficients are set to $\alpha =1$ and $\beta = 1\times 10^{-5}$. In each simulation, the differential Eq. (1) is solved with $N = 8$ basis functions. The calculation of a single simulation takes only a few minutes ($\sim$ 5 min) on a standard computer.

Table 2 Parameters for the random fields motivated by the range of values reported in the literature: for EI(x) [27], for $\rho A(x)$ [4] and for both correlation lengths [50]

The transversal deflection over the time t in the middle of the bridge at $x = L/2$ is shown in Fig. 6 for a single simulation. Its amplitude spectrum is depicted in Fig. 7 and has its maximum at 15.56 Hz (most dominant frequency).

Fig. 6

Vertical deflection in the middle of the bridge resulting from the realization of random fields EI(x) and $\rho A(x)$ and a random traffic flow

Fig. 7

FFT of vertical deflection in the middle of the bridge resulting from the deflection in Fig. 6

For the same single simulation, the transversal acceleration over the time t in the middle of the bridge at $x = L/2$ is shown in Fig. 8. Its amplitude spectrum is depicted in Fig. 9 and shows the same most dominant frequency as the transversal deflection at 15.56 Hz.

Fig. 8

Vertical acceleration in the middle of the bridge resulting from the vertical deflection in Fig. 6

Fig. 9

FFT of vertical acceleration in the middle of the bridge resulting from the acceleration in Fig. 8

A histogram for the most dominant frequencies of all simulations is shown in Fig. 10 (in black line). The average for all most dominant frequencies is 15.59 Hz and its sample standard deviation is 0.13 Hz.

Figure 10 also shows in grey bars the histogram of all most dominant frequencies of the vibration in the middle of the bridge, for which the bending stiffness and the mass per unit length are assumed to be constant (homogeneous beam, $EI_0$ and $\rho A_0$ constant, without random fields) and only the traffic is generated randomly. Here, the average for all most dominant frequencies is 15.66 Hz and its sample standard deviation is 0.06 Hz. A two sample t-test showed that the mean values are statistically significantly different (p-value: $p = 2.13 \times 10^{-21}$).

The system responses of a bridge with the random structural irregularities from Figs. 2 and  3 and without irregularities under the same random realization of the traffic flow are displayed in Fig. 11. The deflections in the middle of the bridge look similar, but the accelerations show differences. The differences in the acceleration can also be seen in the most dominant frequency (with irregularities: 15.59 Hz compared to 15.76 Hz without irregularities) in this particular realization of the traffic flow.

Fig. 10

Histogram for the most dominant frequencies of the vibration in the middle of the bridge of all simulations. The black line depicts the histogram for which the bending stiffness and the mass per unit length are random, the grey bars for which the bending stiffness and the mass per unit length are assumed to be constant

Fig. 11

System responses of a bridge with random structural irregularities (grey lines) and without irregularities (black lines) under the same random realization of the traffic load

A (binomial) logistic model is formulated to assess the probability of a serious structural degradation ($Y=1$) in the bridge based on its bending stiffness. The bridge is classified as defective, if the most dominant frequency falls below 15.4 Hz (minimum of the most dominant frequency from the second Monte Carlo experiment without random fields). Then about 7% of the bridges in the simulations are defective. The logistic model results in

$$\begin{aligned}&P(Y=1 \vert X=\eta )=\frac{e^{-13.13+ 1.03 \times 10^{-9}\eta }}{1+e^{-13.13+ 1.03 \times 10^{-9}\eta }} \end{aligned}$$

(26)

and is shown in Fig. 12. The regression coefficients $\beta _1$ and $\beta _2$ are both statistically significant (p-values $< 1 \times 10^{-9}$). The goodness of fit is measured by the pseudo-R-squared value $R^2_L$ and results in 0.743.

Fig. 12

Fit of the logistic regression model (grey line) to the simulation with serious structural degradation and no serious degradation (black asterisks) with respect to the predictor $\eta$

The maximum bending stress in the bridge is calculated for each simulation. For the sake of simplicity, it was assumed in this study that the cross-section is constant for all simulations. Thus, the normal distance $d_{\bot }(x)$ is constant. The (constant) normal distance $d_{\bot }(x)$ is given by $d_{\bot }(x)=h(x)/2=1/2$. For both Monte Carlo experiments, Fig. 13 shows the distribution of the positions at which the maximum bending stress occurs as histograms. The maximum bending stresses occur mainly in the middle of the bridge. In case of structural irregularities, the points at which the maximum bending stress occurs are somewhat more distributed around the middle of the bridge.

Fig. 13

Histogram of the positions at which the maximum bending stress occurs. The black line depicts the histogram for which the bending stiffness and the mass per unit length are random, the grey bars for which the bending stiffness and the mass per unit length are assumed to be constant

Discussion

In this work we have developed an effective mathematical approach of low computational cost to study the dynamic response of a single span slender beam bridge, in which its random structural irregularities are taken into account. The slender beam bridge is modelled as an Euler–Bernoulli beam and the random structural irregularities are considered by random fields. Also the loads of the random crossing vehicles are taken into account in the simulation model. After Monte Carlo experiments with and without random structural irregularities, each with 400 simulations, the vibrations and bending stresses of the bridge have been determined and statistically analysed.

The transversal deflection and acceleration over the time t are analysed in the middle of the bridge at $x = L/2$ for all simulations. A frequency analysis of the bridge vibrations is a practical way to assess the current condition of the bridge. In particular, the dominant frequencies are a practical quality feature. The dominant frequencies are determined by an amplitude spectrum using FFT. In each simulation the amplitude spectra showed the same most dominant frequency for the transverse deflection and acceleration. Therefore, it does not matter which feature is considered for the frequency analysis. The vertical deflections of the bridge are a more understandable quantity, but the vertical accelerations of a real bridge can be measured more accurately with accelerometers. Therefore, both features are calculated in the simulations.

In the first Monte Carlo experiment (with the random structural irregularities), the average for all 400 most dominant frequencies is 15.59 Hz and its sample standard deviation is 0.13 Hz. In the second Monte Carlo experiment (without irregularities in the structural parameters), the average for all 400 most dominant frequencies is 15.66 Hz and its sample standard deviation is 0.06 Hz. At first glance, the difference between the mean values of the most dominant frequencies of the simulations with and without irregularities in the structural parameters appears small. However, a two sample t-test showed that the mean values are statistically significantly different (p-value: $p = 2.13 \times 10^{-21}$). Other studies that investigated bridge damage with the most dominant frequencies also observed only very small frequency differences between intact and defective bridges [16, 33]. The adequacy of the number of 400 simulations was checked retrospectively by the width of the confidence interval for the most dominant frequencies in the Monte Carlo experiment without irregularities. The width of the 99 % confidence interval resulted in

$$\begin{aligned}\frac{2 \cdot s}{\sqrt{N}} \cdot t_{0.995,N-1} = \frac{2 \cdot 0.06}{\sqrt{400}} \cdot 2.588 = 0.016 \text { Hz} \end{aligned}$$

where s stands for the sample standard deviation and $t_{0.995,N-1}$ for the quantile of the Student’s t-distribution (see [35]). This means that the mean value of the most dominant frequency (without random fields) lies with a probability of 99 % within the confidence interval 15.66±0.008 Hz. This is a sufficiently narrow interval for our purpose.

The system response of a bridge with and without random structural irregularities was also investigated under the same random realization of a traffic load. While the deflections in the middle of the bridge looked very similar with and without irregularities, the accelerations showed differences. These differences can also be seen clearly in the most dominant frequency. Thus, not only the comparison between the two Monte Carlo experiments, but also an arbitrary simulation shows that the random fields and not the traffic load have a significant influence on the most dominant frequency. These results suggest that the influence of the random irregularities on the condition of a bridge may not be negligible.

A (binomial) logistic model was formulated to assess the probability of a serious structural degradation in the bridge based on its bending stiffness. The bridge was classified as defective if the most dominant frequency falls below the minimum of the most dominant frequency from the Monte Carlo experiment without random fields (15.4 Hz). Then about 7 % of the bridges in our simulations were defective. Every year around 2 % of all bridges in Tyrol are assessed to be in an insufficient or poor condition and have to be renovated [31]. The presented simulation approach led to more defective bridges than in reality and is therefore a bit too conservative. The regression coefficients $\beta _1$ and $\beta _2$ in the logistic model are both statistically significant (p-values $< 1 \times 10^{-9}$). In particular, for the regression coefficient $\beta _2$ this means that the logistic regression model depends explicitly on the predictor $\eta$. The goodness of fit was measured by the pseudo-R-squared value $R^2_L$ and results in 0.743. In our opinion, this allows the conclusion that the predictor $\eta$ and the logistic model (22) are acceptable for assessing the probability of serious structural degradation in this bridge.

The results of the investigation come from a fictitious bridge with fictitious traffic and do not correspond to a measured real situation. The parameters for the random fields (see Table 2) are motivated by the range of values reported in the literature. Using these values leads to local maximum variations of the bending stiffness (in Fig. 2$\sim$23% of the mean bending stiffness $EI_0$). Local maximum variations in the bending stiffness up to 25% of the initial bending stiffness were also reported by Maeck et al. [33], who examined a real bridge with various types of damage. It is also plausible that such variations occur in Gaussian random variables with a coefficient of variation of 10%.

For realistic practical applications in future investigations, measurement data of real bridges will be needed. Based on measurement data, field variances can be estimated and suitable autocorrelation functions can be fitted (as it was done, for example, in [11]), so as to generate appropriate random fields.

In the paper, there are three statistical hypotheses in the construction of $r_{EI}(x)$ and $r_{\rho A}(x)$. The first one is stationarity, meaning that the statistical properties of the fields are invariant under translation. This is common practice in stochastic mechanics and reasonable from a modelling perspective; there is no indication nor information that stochastic non-stationarity is present in such random fields for material parameters. The second assumption is the shape of the autocorrelation function $c_{\star }(\Delta )=\text {e}^{-\vert \Delta \vert /l_{\star }}$. This autocorrelation function is in widespread use [19], because it produces sufficiently irregular realizations and is easy to handle both analytically and in Monte Carlo simulations. The third assumption is that the random processes are Gaussian. Apart from the fact that this assumption is also widespread, it greatly facilitates Monte Carlo simulations. It also has the theoretical merit that all statistical properties of a Gaussian process are completely determined by its mean, variance and autocorrelation function. For the purpose of demonstrating our results, Gaussian random fields suffice. However, non-Gaussian random fields could be used just the same.

A limitation of the simulation model is also that only transversal deflections are considered and thus the torsion and the lateral deflections of the bridge are not taken into account. The bridge in this study is assumed to be slender and therefore the torsion can be neglected. Monte Carlo experiments can be computationally very expensive. To save computing time, we have used this simplified simulation model. However, most of the concepts presented in this work can easily be extended to more sophisticated simulation models.

Conclusion and outlook

In this study there are essentially two main conclusions.

First, from our point of view, this study is the first work that takes into account spatial random structural irregularities in bridges under random traffic loads. The developed approach enables a better understanding of the vibrations of bridges. Especially the comparison between the Monte Carlo experiments with and without irregularities shows that the influence of the random irregularities on the stability status of a bridge may not be negligible. For a clearer statement, we need measurement data of real bridges.

Second, we have presented an approach with which the probability of serious structural degradation of the bridge can be assessed by means of the bending stiffness EI(x) or, more precisely, by the predictor $\eta$ using a logistic regression model.

Structural degradation in bridges are often detected by a frequency analysis of measured vibration data. This method is useful if the bridge has been monitored and the frequency data have been collected for a long period of time. But if no comparative data for the bridge are available, the question arises as to the critical (limit) frequency at which the bridge is considered defective. With the Monte Carlo simulation, however, one has the possibility to estimate a limit frequency as the minimum frequency from the simulation without irregularities. The frequency analysis provides the information that a bridge is damaged, but it is difficult to locate the area and the extent of the structural degradation. Furthermore, the differences in the dominant frequencies between an intact and defective bridge are usually very small. Especially in the case of local damages, the differences in the frequencies are very small. That is why we are currently developing a mathematical tool that will enable improved damage and structural degradation detection in bridges based on measurement data. An inverse problem formulation will be used, with which it is possible to determine the spatially distributed bending stiffness EI(x) of the bridge [12]. The (binomial) logistic regression model that is generated with the presented approach then allows one to assess the probability of a serious structural degradation in the bridge. In addition, the position of the serious degradation zone can be localized more precisely using the spatial bending stiffness EI(x) curve.

This work is mainly a method paper with the aim of presenting the proposed method and it will form the basis for ongoing research into improved damage or serious structural degradation detection in real bridges. The model will be used for in-depth studies of the effects of different scenarios and the influences of changing the material and the traffic parameters.

Spectral Method for the Dynamic Euler–Bernoulli Beam

The differential equation (1) is solved by the spectral method [36]. To do this, the ansatz

$$\begin{aligned} w(x,t)=&\sum _{k=0}^{\infty }b_k(t)\varphi _k(x) \nonumber \\ \approx&\sum _{k=0}^{N}b_k(t)\varphi _k(x)={\mathbf {b}}(t)^T\varvec{\varphi }(x) \end{aligned}$$

(27)

with the vector of unknown linear coefficients

$$\begin{aligned}{\mathbf {b}}(t) =(b_k(t))_{k=1}^N\end{aligned}$$

and the vector of the basis functions (17)

$$\begin{aligned} \varvec{\varphi }(x)=(\varphi _k(x))_{k=1}^N \end{aligned}$$

for a given number N is substituted into the beam Eq. (1)

$$\begin{aligned}&\left( EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\right) _{xx}\\&\qquad +\rho A(x) \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{tt}\\&\qquad +\beta \left( EI(x)\left( \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _t\right) _{xx}\right) _{xx}\\&\qquad +\alpha \rho A(x) \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{t}\\&\quad =f(x,t). \end{aligned}$$

The equation is multiplied with the basis function $\varphi _l(x)$ (for $l=1,...,N$) and integrated over the whole bridge from $x=0$ to $x=L$:

$$\begin{aligned}&\int _{0}^{L} \left( EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\right) _{xx}\varphi _l(x) \,\text {d}x \nonumber \\&\qquad +\int _{0}^{L}\rho A(x) \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{tt} \varphi _l(x) \,\text {d}x \nonumber \\&\qquad +\int _{0}^{L}\beta \left( EI(x)\left( \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _t\right) _{xx}\right) _{xx}\varphi _l(x) \,\text {d}x\nonumber \\&\qquad +\int _{0}^{L}\alpha \rho A(x) \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{t} \varphi _l(x) \,\text {d}x \nonumber \\&\quad =\int _{0}^{L} f(x,t) \varphi _l(x) \,\text {d}x. \end{aligned}$$

(28)

We start with the first term

$$\begin{aligned} \int _{0}^{L}\left( EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\right) _{xx}\varphi _l(x) dx. \end{aligned}$$

After partial integration we get

$$\begin{aligned} \left( EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\right) _{x}\varphi _l(x)\Big \vert _{x=0}^L\\ -\int _{0}^{L}\left( EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\right) _{x}\varphi _l(x)_x dx. \end{aligned}$$

Since the basis functions $\varphi _l(x)$ fulfill the boundary conditions (2) the first part vanishes and we get for the first term

$$\begin{aligned} - \int _{0}^{L}\left( EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\right) _{x}\varphi _l(x)_x dx. \end{aligned}$$

Applying partial integration again, the term results in

$$\begin{aligned}&-\sum _{k=0}^{N}b_k(t)\left( EI(x)\varphi _k(x)_{xx}\varphi _l(x)_x\right) \Big \vert _{x=0}^L\\&\quad +\int _{0}^{L}EI(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{xx}\varphi _l(x)_{xx} dx. \end{aligned}$$

Using the boundary conditions (2) we finally get for the first term in Eq. (28)

$$\begin{aligned} \sum _{k=0}^{N}b_k(t)\underbrace{\int _{0}^{L}EI(x)\varphi _k(x)_{xx}\varphi _l(x)_{xx} dx}_{=:{\mathbf {M}}_{lk}}. \end{aligned}$$

(29)

The second term of Eq. (28) yields

$$\begin{aligned}&\int _{0}^{L} \rho A(x)\left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{tt} \varphi _l(x) dx \nonumber \\&\quad = \int _{0}^{L} \rho A(x) \sum _{k=0}^{N}b_k(t)_{tt}\varphi _k(x) \varphi _l(x) dx\nonumber \\&\quad = \sum _{k=0}^{N}b_k(t)_{tt} \underbrace{\int _{0}^{L} \rho A(x) \varphi _k(x) \varphi _l(x) dx}_{=:{\mathbf {K}}_{lk}} . \end{aligned}$$

(30)

For the third and fourth term in Eq. (28), we have almost the same calculation as for the first (29) and second term (30). The difference is using $w_t$ instead of w. So we get for the third term

$$\begin{aligned}&\int _{0}^{L}\beta \left( EI(x)\left( \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _t\right) _{xx}\right) _{xx}\varphi _l(x) \,\text {d}x \end{aligned}$$

(31)

$$\begin{aligned}&\quad =\beta \cdot \sum _{k=0}^{N}b_k(t)_t\underbrace{\int _{0}^{L}EI(x)\varphi _k(x)_{xx}\varphi _l(x)_{xx} dx}_{={\mathbf {M}}_{lk}}. \end{aligned}$$

(32)

and for the fourth term

$$\begin{aligned}&\int _{0}^{L}\alpha \rho A(x) \left( \sum _{k=0}^{N}b_k(t)\varphi _k(x)\right) _{t} \varphi _l(x) \,\text {d}x \end{aligned}$$

(33)

$$\begin{aligned}&\quad =\alpha \cdot \sum _{k=0}^{N}b_k(t)_{t} \underbrace{\int _{0}^{L} \rho A(x) \varphi _k(x) \varphi _l(x) dx}_{={\mathbf {K}}_{lk}}. \end{aligned}$$

(34)

The force term on the right hand side in equation (28) results in

$$\begin{aligned} \int _{0}^{L}&f(x,t) \varphi _l(x) \,\text {d}x\\ =&\int _{0}^{L} \sum _{i=1}^{N_a} P_i\delta (x-(v_it-s_i))[\sigma (v_it-s_i)\\&-\sigma (v_it-(s_i+L))]\varphi _l(x) \, \text {d}x\\ =&\sum _{i=1}^{N_a} P_i \int _{0}^{L} \delta (x-(v_it-s_i))[\sigma (v_it-s_i)\\&-\sigma (v_it-(s_i+L))] \varphi _l(x) \, \text {d}x\\ =&\sum _{i=1}^{N_a} P_i \varphi _l(v_it-s_i)[\sigma (v_it-s_i)\\&-\sigma (v_it-(s_i+L))] =:{\mathbf {f}}_{l}(t) \end{aligned}$$

for $l=1,...,N$.

After substituting all these results into Eq. (28), we get the system of linear ordinary differential equations of second order

$$\begin{aligned}&{\mathbf {M}} \cdot {\mathbf {{b}}}(t)_{tt}+\left( \beta {\mathbf {K}} +\alpha {\mathbf {M}} \right) \cdot \mathbf {{b}}(t)_{t} + {\mathbf {K}} \cdot {\mathbf {b}}(t)= {\mathbf {f}}(t) \end{aligned}$$

(35)

with mass matrix ${\mathbf {M}}$, matrix ${\mathbf {K}}$ and vector ${\mathbf {f}}(t)$ with entries ${\mathbf {M}}_{lk}$, ${\mathbf {K}}_{lk}$ and ${\mathbf {f}}_{l}(t)$ for $l = 1,...,N$ and $k = 1,...,N$.