Skip to main content
SpringerLink
Log in

Nonlinear Vibrations of Simply Supported Cylindrical Panels with Uncertain Parameters: An Intrusive Application of the Generalized Polynomial Chaos Expansion

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

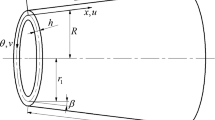
This work investigates a simply supported cylindrical panel (with uncertainties in its thickness, radius and Young’s modulus) subjected to a time-dependent transverse load.

Methods

The nonlinear equilibrium equations of the panel are obtained from Donnell’s shallow shell theory, in terms of the transverse displacement field and Airy’s stress function. To discretize this set of equations, the standard Galerkin method is applied in the panel’s space domain. For that, a consistent modal solution for the transverse displacement field is chosen from a perturbation method, considering the main modal couplings that occur due to the geometric nonlinearities present in the equilibrium equations. The uncertainties of the parameters are assumed to have a uniform probability density function and are considered in the nonlinear equilibrium equations by a generalized polynomial chaos expansion of the modal amplitudes of the transverse displacement field. Legendre-chaos polynomials are used to describe the random parameters and the stochastic Galerkin method is applied to discretize the expanded nonlinear equilibrium equations in the random parameter space.

Results

The mean and variance of the bifurcation diagrams are obtained, evaluating the influence of uncertain parameters on their paths, and the regions, where an intrusive application of a generalized polynomial chaos expansion procedure can be applied.

Conclusions

The numerical results show good agreement between the proposed procedure and the results obtained by the Monte Carlo method in the bifurcation diagrams, especially those regions that do not have dynamic jumps and/or competition between the periodic, quasi-periodic and chaotic permanent response.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Liew KM, Lim CW, Kitipornchai S (1997) Vibration of shallow shells: a review with bibliography. Appl Mech Rev. https://doi.org/10.1115/1.3101731

    Article  Google Scholar 

  2. Qatu MS (2002) Recent research advances in the dynamic behavior of shells: 1989–2000, part 2: homogeneous shells. Appl Mech Rev. https://doi.org/10.1115/1.1483078

    Article  Google Scholar 

  3. Amabili M, Païdoussis MP (2003) Review of studies on geometrically nonlinear vibrations and dynamics of circular cylindrical shells and panels, with and without fluid-structure interaction. Appl Mech Rev 56:349–356

    Article  Google Scholar 

  4. Alijani F, Amabili M (2014) Non-linear vibrations of shells: a literature review from 2003 to 2013. Int J Non-Linear Mech 58:233–257

    Article  Google Scholar 

  5. Moussaoui F, Benamar R (2002) NON-linear vibrations of shell-type structures: a review with bibliography. J Sound Vib. https://doi.org/10.1006/jsvi.2001.4146

    Article  Google Scholar 

  6. Hasrati E, Ansari R, Torabi J (2017) Nonlinear forced vibration analysis of FG-CNTRC cylindrical shells under thermal loading using a numerical strategy. Int J Appl Mech. https://doi.org/10.1142/S1758825117501083

    Article  Google Scholar 

  7. Hasrati E, Ansari R, Torabi J (2018) A novel numerical solution strategy for solving nonlinear free and forced vibration problems of cylindrical shells. Appl Math Model 53:653–672. https://doi.org/10.1016/j.apm.2017.08.027

    Article  MathSciNet  MATH  Google Scholar 

  8. Ansari R, Torabi J, Hasrati E (2020) Postbuckling analysis of axially-loaded functionally graded GPL-reinforced composite conical shells. Thin-Walled Struct. https://doi.org/10.1016/j.tws.2019.106594

    Article  Google Scholar 

  9. Touzé C, Amabili M (2006) Nonlinear normal modes for damped geometrically nonlinear systems: application to reduced-order modelling of harmonically forced structures. J Sound Vib 298:958–981. https://doi.org/10.1016/j.jsv.2006.06.032

    Article  Google Scholar 

  10. Amabili M, Touzé C (2007) Reduced-order models for nonlinear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic nonlinear normal modes methods. J Fluids Struct 23:885–903. https://doi.org/10.1016/j.jfluidstructs.2006.12.004

    Article  Google Scholar 

  11. Gonçalves PB, Silva FMA, del Prado ZJGN (2008) Low-dimensional models for the nonlinear vibration analysis of cylindrical shells based on a perturbation procedure and proper orthogonal decomposition. J Sound Vib 315:641–663. https://doi.org/10.1016/J.JSV.2008.01.063

    Article  Google Scholar 

  12. Grigoriu M (2000) Stochastic mechanics. Int J Solids Struct. https://doi.org/10.1016/S0020-7683(99)00088-8

    Article  MATH  Google Scholar 

  13. Xiu D (2009) Fast numerical methods for stochastic computations: a review. Commun Comput Phys 5:242–272

  14. Xiu D (2010) Numerical methods for stochastic computations. Princeton University Press

    Book  MATH  Google Scholar 

  15. Xiu D, Karniadakis GE (2002) The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J Sci Comput. https://doi.org/10.1137/S1064827501387826

    Article  MathSciNet  MATH  Google Scholar 

  16. Ghanem RG, Spanos PD (2003) Stochastic finite elements: a spectral approach. Dover Publications. ISBN 0-486-42818-4

  17. Sudret B, der Kiureghian A (2000) Stochastic finite element methods and reliability : a state-of-the-art report. University of California

    Google Scholar 

  18. Ernst OG, Mugler A, Starkloff H-J, Ullmann E (2012) On the convergence of generalized polynomial chaos expansions. ESAIM. https://doi.org/10.1051/m2an/2011045

  19. Wiener N (1938) The homogeneous chaos. Am J Math. https://doi.org/10.2307/2371268

    Article  MathSciNet  MATH  Google Scholar 

  20. Gel A, Garg R, Tong C et al (2013) Applying uncertainty quantification to multiphase flow computational fluid dynamics. Powder Technol. https://doi.org/10.1016/j.powtec.2013.01.045

    Article  Google Scholar 

  21. Ávila da Silva Jr CR, Teófilo Beck A (2011) Chaos-Galerkin solution of stochastic Timoshenko bending problems. Comput Struct 89:599–611. https://doi.org/10.1016/j.compstruc.2011.01.002

  22. Bahmyari E, Khedmati MR, Soares G (2017) Stochastic analysis of moderately thick plates using the generalized polynomial chaos and element free Galerkin method. Eng Anal Boundary Elem 79:23–37. https://doi.org/10.1016/j.enganabound.2017.03.001

    Article  MathSciNet  MATH  Google Scholar 

  23. Seçgin A, Kara M, Ferguson N (2021) Discrete singular convolution–polynomial chaos expansion method for free vibration analysis of non-uniform uncertain beams. JVC/J Vibr Control. https://doi.org/10.1177/1077546320988190

    Article  Google Scholar 

  24. Pascual B, Adhikari S (2012) A reduced polynomial chaos expansion method for the stochastic finite element analysis. Sadhana 37:319–340. https://doi.org/10.1007/s12046-012-0085-1

  25. Liang K, Sun Q, Liu X (2018) Investigation on imperfection sensitivity of composite cylindrical shells using the nonlinearity reduction technique and the polynomial chaos method. Acta Astronaut 146:349–358. https://doi.org/10.1016/j.actaastro.2018.03.018

    Article  Google Scholar 

  26. Dey S, Mukhopadhyay T, Sahu SK, Adhikari S (2016) Effect of cutout on stochastic natural frequency of composite curved panels. Compos B Eng 105:188–202. https://doi.org/10.1016/J.COMPOSITESB.2016.08.028

    Article  Google Scholar 

  27. Sepahvand K, Marburg S, Hardtke H-J (2012) Stochastic free vibration of orthotropic plates using generalized polynomial chaos expansion. J Sound Vib. https://doi.org/10.1016/j.jsv.2011.08.012

    Article  MATH  Google Scholar 

  28. Singh BN, Yadav D, Iyengar NGR (2001) Stability analysis of laminated cylindrical panels with uncertain material properties. Compos Struct 54:17–26. https://doi.org/10.1016/S0263-8223(01)00065-4

  29. Singh BN, Yadav D, Iyengar NGR (2002) Free vibration of composite cylindrical panels with random material properties. Compos Struct 58:435–442. https://doi.org/10.1016/S0263-8223(02)00133-2

  30. Amabili M (2008) Nonlinear vibrations and stability of shells and plates. Cambridge University Press

    Book  MATH  Google Scholar 

  31. Donnell LH, Ohio A (1934) A new theory for the buckling of thin cylinders under axial compression and bending. ASME Aeronaut Eng 56–12:795–806

    Google Scholar 

  32. Amabili M (2005) Nonlinear vibrations of circular cylindrical panels. J Sound Vib 281:509–535. https://doi.org/10.1016/J.JSV.2004.01.021

    Article  Google Scholar 

  33. Gonçalves PB, Silva FMA, del Prado ZJGN (2016) Reduced order models for the nonlinear dynamic analysis of shells. Proc IUTAM 19:118–125. https://doi.org/10.1016/J.PIUTAM.2016.03.016

    Article  Google Scholar 

  34. Silva FMA, Gonçalves PB, del Prado ZJGN (2011) An alternative procedure for the non-linear vibration analysis of fluid-filled cylindrical shells. Nonlinear Dyn 66:303–333. https://doi.org/10.1007/s11071-011-0037-z

    Article  MathSciNet  Google Scholar 

  35. Morais JL, Silva FMA (2019) Influence of modal coupling and geometrical imperfections on the nonlinear buckling of cylindrical panels under static axial load. Eng Struct 183:816–829. https://doi.org/10.1016/J.ENGSTRUCT.2018.12.032

    Article  Google Scholar 

  36. Rodrigues L, Silva FMA, Gonçalves PB, del Prado ZJGN (2014) Effects of modal coupling on the dynamics of parametrically and directly excited cylindrical shells. Thin-Walled Struct 81:210–224. https://doi.org/10.1016/J.TWS.2013.08.004

    Article  Google Scholar 

  37. Rodrigues L, Silva FMA, Gonçalves PB (2020) Influence of initial geometric imperfections on the 1:1:1:1 internal resonances and nonlinear vibrations of thin-walled cylindrical shells. Thin-Walled Struct. https://doi.org/10.1016/j.tws.2020.106730

    Article  Google Scholar 

  38. Rodrigues L, Silva FMA, Gonçalves PB (2022) Effect of geometric imperfections and circumferential symmetry on the internal resonances of cylindrical shells. Int J Non-Linear Mech 139:103875

    Article  Google Scholar 

  39. Silva FMA, Sattler HAR, Gonçalves PB, del Prado ZJGN (2016) Influence of modal coupling on the nonlinear vibration of simply supported cylindrical panels. Appl Mech Mater 849:106–118. https://doi.org/10.4028/www.scientific.net/AMM.849.106

    Article  Google Scholar 

  40. da Silva FMA, Brazão AF, Gonçalves PB (2015) Influence of physical and geometrical uncertainties in the parametric instability load of an axially excited cylindrical shell. Math Probl Eng. https://doi.org/10.1155/2015/758959

    Article  MathSciNet  MATH  Google Scholar 

  41. Palla AEF (2020) Application of polynomial chaos for analysis of stochastic resonance curves of cylindrical panels [in Portuguese]. Master thesis. Federal University of Goiás.

  42. Gerritsma M, van der Steen JB, Vos P, Karniadakis G (2010) Time-dependent generalized polynomial chaos. J Comput Phys 229:8333–8363. https://doi.org/10.1016/j.jcp.2010.07.020

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was made possible by the support of the Brazilian agencies: CNPq and FAPEG. Anna Elizabete F. Palla acknowledges the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), which part-financed her studies.

Author information

Authors and Affiliations

  1. School of Civil and Environmental Engineering, Federal University of Goiás, UFG, Av. Universitária, no. 1488, Setor Universitário, Goiânia, GO, CEP: 74605-220, Brazil

    Anna Elizabete F. Palla & Frederico M. A. Silva

Authors
  1. Anna Elizabete F. Palla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Frederico M. A. Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Frederico M. A. Silva.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Palla, A.E.F., Silva, F.M.A. Nonlinear Vibrations of Simply Supported Cylindrical Panels with Uncertain Parameters: An Intrusive Application of the Generalized Polynomial Chaos Expansion. J. Vib. Eng. Technol. 10, 2917–2934 (2022). https://doi.org/10.1007/s42417-022-00527-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00527-7

Keywords

Search

Navigation