Skip to main content
SpringerLink
Log in

Singular Function Model of Concentrated Mass-Cable Composite Structures

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

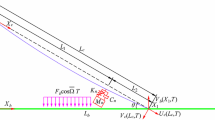
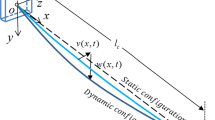
The concentrated mass on a cable has a great influence on the natural frequency of cable structures. In view of the complex of calculation process of transfer matrix method, this paper presents an analytical model to investigate the vibration characteristics of cable structures with concentrated masses.

Methods

In the present model, the vibration model of the cable structure with concentrated masses is expressed using singular functions. To validate the present model, the experiments of the frequency measurement using laser pickup method were also carried out.

Results

Analytical expression of frequencies of cable structures with concentrated masses is derived. As an application of the present model, the influences of the size, quantity and position of the concentrated mass of the cable on the cable natural frequency are also examined and discussed.

Conclusions

The comparison of the experimental results and model predictions shows that the singular function model can predict well the influence of concentrated mass on the natural frequency of cable structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Martin B, Salehian A (2016) Mass and stiffness effects of harnessing cables on structural dynamics: continuum modeling. AIAA J 54(9):2881–2904. https://doi.org/10.2514/1.J054156

    Article  Google Scholar 

  2. Yerrapragada K, Salehian A (2019) Analytical study of coupling effects for vibrations of cable harnessed beam structures. J Vib Acoust 141(3):031001. https://doi.org/10.1115/1.4042042

    Article  Google Scholar 

  3. Agrawal P, Salehian A (2021) Damping mechanisms in cable-harnessed structures for space applications: analytical modeling. J Vib Acoust 143(2):021001. https://doi.org/10.1115/1.4047881

    Article  Google Scholar 

  4. Agrawal P, Salehian A (2021) Continuum modeling and vibration analysis of cable-harnessed plate structures of periodic patterns. J Vib Acoust 143(6):4050713. https://doi.org/10.1115/1.4050713

    Article  Google Scholar 

  5. Li ZJ, Li P, He Z, Cao P (2013) Static and free vibration analysis of shallow sagging inclined cables. Struct Eng Mech 45(2):145–157. https://doi.org/10.12989/sem.2013.45.2.145

    Article  Google Scholar 

  6. Pakos W (2019) Free vibration of a sagged cable with attached discrete elements. Appl Math Mech 40(5):631–648. https://doi.org/10.1007/s10483-019-2479-6

    Article  MathSciNet  Google Scholar 

  7. Kang HJ, Zhao YY, Zhu HP (2013) Out-of-plane free vibration analysis of a cable-arch structure. J Sound Vib 332(4):907–921. https://doi.org/10.1016/j.jsv.2012.10.007

    Article  Google Scholar 

  8. Fei H, Zichen D, Danhui D (2020) A novel method for dynamic analysis of complex multi-segment cable systems. Mech Syst Signal Process 142:106780. https://doi.org/10.1016/j.ymssp.2020.106780

    Article  Google Scholar 

  9. Hong SC, Zou DJ, Wei MH, Lin K (2016) Effects of supporting member on the nonlinear parametric resonance of a cable. Int J Struct Stab Dyn 16(2):1450096. https://doi.org/10.1142/S0219455414500965

    Article  MathSciNet  MATH  Google Scholar 

  10. Wu YS, Zhang WZ, Meng XY, Su Y (2016) Nonlinear vibration control of cable net structures with bounded uncertainties. Acta Mech 227(10):2985–3000. https://doi.org/10.1007/s00707-016-1656-8

    Article  MathSciNet  MATH  Google Scholar 

  11. Kye S, Jung HJ, Jung HY (2019) Experimental investigation on a cable structure equipped with an electrodynamic damper and its monitoring strategy through energy harvesting. Sensors 19(11):2631. https://doi.org/10.3390/s19112631

    Article  Google Scholar 

  12. Yang Y, Sanchez L, Zhang H, Roeder A, Bowlan J, Crochet J, Farrar C, Mascareñas D (2019) Estimation of full-field, full-order experimental modal model of cable vibration from digital video measurements with physics-guided unsupervised machine learning and computer vision. Struct Control Health Monit 26(6):e2358. https://doi.org/10.1002/stc.2358

    Article  Google Scholar 

  13. Jafari M, Sarkar PP (2020) Wind-induced response characteristics of a yawed and inclined cable in ABL wind: experimental- and numerical-model based study. Eng Struct 214:110681. https://doi.org/10.1016/j.engstruct.2020.110681

    Article  Google Scholar 

  14. Xu J, Zhang Y, Zhao Q, Zhang L (2022) Experiment and simulation analysis on dynamic response of plane cable-membrane structure under impact load. Thin-Walled Struct 171:108814. https://doi.org/10.1016/j.tws.2021.108814

    Article  Google Scholar 

  15. Balaji PS, Selvakumar KK (2021) Applications of nonlinearity in passive vibration control: a review. J Vib Eng Technol 9:183–213. https://doi.org/10.1007/s42417-020-00216-3

    Article  Google Scholar 

  16. Chang W, Jin X, Huang Z (2021) Random response of nonlinear system with inerter-based dynamic vibration absorber. J Vib Eng Technol. https://doi.org/10.1007/s42417-021-00334-6

    Article  Google Scholar 

  17. Wang Z, Gao H, Xu Y, Chen Z (2019) Experimental study on the improving effect of inertial mass on vibration control of stay cables with dampers. J Vib Eng 32(03): 377–385. https://kns.cnki.net/kcms/detail/detail.aspx?FileName=ZDGC201903001&DbName=CJFQ2019

  18. Lu L, Duan Y, Spencer BFJ (2017) Inertial mass damper for mitigating cable vibration. Struct Control Health Monit 24(10):1–12. https://doi.org/10.1002/stc.1986

    Article  Google Scholar 

  19. Sun L, Hong D, Chen L (2017) Cables interconnected with tuned inerter damper for vibration mitigation. Eng Struct 151(15):57–67. https://doi.org/10.1016/j.engstruct.2017.08.009

    Article  Google Scholar 

  20. Ahmad J, Cheng S (2013) Effect of cross-link stiffness on the in-plane free vibration behaviour of a two-cable network. Eng Struct 52:570–580. https://doi.org/10.1016/j.engstruct.2013.03.018

    Article  Google Scholar 

  21. Sergev SS, Iwan WD (1981) The natural frequencies and mode shapes of cables with attached masses. J Energy Res Technol 103(3):237. https://doi.org/10.1115/1.3230844

    Article  Google Scholar 

  22. Yu P (1997) Explicit vibration solutions of a cable under complicated loads. J Appl Mech 64(4):957–964. https://doi.org/10.1115/1.2789006

    Article  MATH  Google Scholar 

  23. Zhou H, Zhou X, Yao G, Sun L, Xing F (2019) Free vibration of two taut cables interconnected by a damper. Struct Control Health Monit 26:e2423. https://doi.org/10.1002/stc.2423

    Article  Google Scholar 

  24. Deng Z, Tang H, Li Y (2020) Experimental research on the wind-induced vibration of stay cable with lighting fixtures. Journal of Vibration and Shock 39(06): 44–50. https://kns.cnki.net/kcms/detail/detail.aspx?FileName=ZDCJ202006007&DbName=CJFQ202010.13465/j.cnki.jvs.2020.06.007

  25. Wu J (1987) Unified treatment of concentration and distribution. Mech Eng (04):16–20. https://kns.cnki.net/kcms/detail/detail.aspx?FileName=LXYS198704002&DbName=CJFQ1987

  26. Wang X (1985) The solutions of some generalized ordinary differential equations contained singularity functions and its applications to mechanics. Mech Eng (02):91–98. https://kns.cnki.net/kcms/detail/detail.aspx?FileName=GCSX198502012&DbName=CJFQ1985

  27. Wu X (2005) Natural transversal vibrating frequency of continuous long cable with multi-spans. J Vib Shock (04):127–128+146. https://kns.cnki.net/kcms/detail/detail.aspx?FileName=ZDCJ200504037&DbName=CJFQ2005

  28. Quagliaroli M, Malerba PG, Albertin A, Pollini N (2015) The role of prestress and its optimization in cable domes design. Comput Struct 161:17–30. https://doi.org/10.1016/j.compstruc.2015.08.017

    Article  Google Scholar 

  29. Wang ZW, Li TJ (2015) Nonlinear dynamic analysis of parametrically excited space cable-beam structures due to thermal loads. Eng Struct 83:50–61. https://doi.org/10.1016/j.engstruct.2014.11.001

    Article  Google Scholar 

  30. Chen Y, Feng J (2012) Generalized eigenvalue analysis of symmetric prestressed structures using group theory. J Comput Civ Eng 26(4):488–497. https://doi.org/10.1061/(ASCE)CP.1943-5487.0000151

    Article  Google Scholar 

  31. Chen Y, Feng J (2016) Improved symmetry method for the mobility of regular structures using graph products. J Struct Eng 142(9):04016051. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001512

    Article  Google Scholar 

  32. Chen Y, Feng J, Lv HZ, Sun Q (2018) Symmetry representations and elastic redundancy for members of tensegrity structures. Compos Struct 203:672–680. https://doi.org/10.1016/j.compstruct.2018.07.044

    Article  Google Scholar 

  33. Lyu LF, Zhu WD (2021) Operational modal analysis of a rotating structure under ambient excitation using a tracking continuously scanning laser Doppler vibrometer system. Mech Syst Signal Process 152(1):107367. https://doi.org/10.1016/j.ymssp.2020.107367

    Article  Google Scholar 

  34. Rothberg SJ, Allen MS, Castellini P (2016) An international review of laser Doppler vibrometry: making light work of vibration measurement. Opt Lasers Eng 99:11–22. https://doi.org/10.1016/j.optlaseng.2016.10.023

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge the financial support received from the National Natural Science Foundation of China (Grant Nos. 51978406, 51520105012).

Author information

Authors and Affiliations

  1. Guangdong Provincial Key Laboratory of Durability for Marine Civil Engineering, College of Civil and Transportation Engineering, Shenzhen University, Shenzhen, People’s Republic of China

    Deyou Liu, Bingjie Song & Dawang Li

  2. Logistics Department, Henan Provincial People’s Hospital, Henan, People’s Republic of China

    Chenghui Jia

Authors
  1. Deyou Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chenghui Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bingjie Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dawang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dawang Li.

Ethics declarations

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, D., Jia, C., Song, B. et al. Singular Function Model of Concentrated Mass-Cable Composite Structures. J. Vib. Eng. Technol. 10, 2657–2667 (2022). https://doi.org/10.1007/s42417-022-00510-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00510-2

Keywords

Search

Navigation