Skip to main content
SpringerLink
Log in

Defect Characterization in a 1D Spring Mass System Using the Laplace and Z-Transforms

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

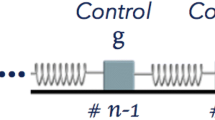
We present a scheme to characterize the defects within a one-dimensional spring–mass system comprised of an arbitrary number of bodies with otherwise uniform masses connected in series by springs using only a discrete set of vibrational data of the first body.

Methods

The system of ordinary differential equations modeling spring–mass systems was analyzed using the Laplace transform with the unknown mass and location of the defects as parameters. We propose a two-phase strategy to determine these unknown parameters using a set of discrete measurements of the longitudinal displacements of the first mass after the system is excited by a Dirac \(\delta\) impulse on the first mass. The Z-transform of the discrete time-measurements is used to obtain an approximation for the Laplace-domain solution curve of the vibration of the first body. First, we show how the poles of this simulated data can be used to determine the masses of the defects. Then the location of these defects were calculated using an optimization routine.

Results

We also show several simulations with two defects highlighting the instances when the scheme is highly accurate as well as its limitations. In these cases, the algorithm was able to predict the mass and locations accurately.

Conclusions

In this paper, we were able to design a stable numerical scheme that can characterize the defects, i.e., estimate their masses and locations, using only a discrete set of vibrational data of the first mass.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Availability of data and material

Not applicable.

Code availability

Not applicable.

References

  1. Akulenko LD, Nesterov SV (2014) Mass defect influence on the longitudinal vibration frequencies and mode shapes of a beam. Mech Solids 49:104–111

    Article  Google Scholar 

  2. Bae J-S, Hwang J-H, Kwag D-G, Park J, Inman DJ (2014) Vibration suppression of a large beam structure using tuned mass damper and eddy current damping. Shock Vib 1–10:2014

    Google Scholar 

  3. Caniato M, Bettarello F, Marsich L, Ferluga A, Sbaizero O, Schmid C (2016) Impulse response method for defect detection in polymers: description of the method and preliminary results. Polym Test 55:78–87

    Article  Google Scholar 

  4. Clark W (2000) Vibration control with state-switched piezoelectric materials. J Intell Mater Syst Struct 11(4):263–271

    Article  Google Scholar 

  5. Corr L, Clark W (2003) A novel semi-active multi-modal vibration control law for a piezoceramic actuator. J Vib Acoust 125(2):214–222

    Article  Google Scholar 

  6. Deymier P, Runge K (2016) One-dimensional mass-spring chains supporting elasticwaves with non-conventional topology. Crystals 6(4):44

    Article  Google Scholar 

  7. Dove MT (2011) Introduction to the theory of lattice dynamics. JDN 12:123–159

    Article  Google Scholar 

  8. Egarguin NJA, Meklachi T, Onofrei D, Harari-Arnold ND (2020) Correction to: Vibration suppression and defect detection schemes in 1D linear spring-mass systems. J Vib Eng Technol 8:621

    Article  Google Scholar 

  9. Egarguin NJA, Meklachi T, Onofrei D, Harari-Arnold ND (2020) Vibration suppression and defect detection schemes in 1d linear spring-mass systems. J Vib Eng Technol 8:489–503

    Article  Google Scholar 

  10. El Saif M, Foda MA (2001) Vibration suppression of a beam structure of intermediate masses and springs. J Sound Vib 256(4):629–645

    Google Scholar 

  11. Faleski Michael C (2006) Transient behavior of the driven rlc circuit. Am J Phys 74(5):429–437

    Article  Google Scholar 

  12. Getachew G (2018) A review of simple harmonic motion for mass spring system and its analogy to the oscillations in lc circuit. J Phys Chem Sci 6(3)

  13. He ZC, Xiao X, Li E (2017) Design for structural vibration suppression in laminate acoustic metamaterials. Compos Part B Eng 131:237–252

    Article  Google Scholar 

  14. Horn RA, Johnson CR (2013) Matrix analysis, 2nd edn. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  15. Jarrousse O (2012) Modified mass–spring system for physically based deformation modeling. Ph.D. thesis

  16. Joannopoulos JD, Johnson SG, Winn JN, Meade RD (2008) Photonic crystals: molding the flow of light, 2nd edn. Princeton University Press, Princeton

    MATH  Google Scholar 

  17. Li T, Li Q, Liu T (2019) An actuated dissipative spring-mass walking model: predicting human-like ground reaction forces and the effects of model parameters. J Biomech 90:58–64

    Article  Google Scholar 

  18. Liu T, Bargteil AW, O’Brien JF, Kavan L (2013) Fast simulation of mass–spring systems. ACM Trans Gr 32(6):1–7

    Google Scholar 

  19. Martin WC, Wu A, Geyer H (2015) Robust spring mass model running for a physical bipedal robot. In: 2015 IEEE international conference on robotics and automation (ICRA), Seattle, WA, USA, pp 6307–6312

  20. Minaya R, Ponce Y (2017) Applications of spring–mass model on crystalline lattices. 09

  21. Morgan D, Qiao S (2008) Accuracy and stability in mass-spring systems for sound synthesis. In: Proceedings of C3S2E-08, pp 1–12

  22. Nealan A, Muler M, Keiser R, Boxerman E, Carlson M (2005) Physically based deformable models in computer graphics. Comput Gr Forum 25(4):809–836

    Article  Google Scholar 

  23. Nedel L, Thalmann D (1998) Real time muscle deformations using mass-spring systems. In: Proceedings of the computer graphics international, pp 157–177

  24. Patel VN, Tandon N, Pandey RK (2012) Defect detection in deep groove ball bearing in presence of external vibration using envelope analysis and duffing oscillator. Measurement 45(5):960–970

    Article  Google Scholar 

  25. Peng H, Frank Pai P (2014) Acoustic metamaterial plates for elastic wave absorption and structural vibration suppression. Int J Mech Sci 89:350–361

    Article  Google Scholar 

  26. André Preumont (2011) Vibration control of active structures, an introduction. Solid mechanics and its applications, 3rd edn. Springer, Berlin

    Google Scholar 

  27. Qin Y, Xiang C, Wang Z, Dong M (2017) Road excitation classification for semi-active suspension system based on system response. J Vib Control 24(13):2732–2748

    Article  Google Scholar 

  28. Radetzky A, Nurnberger A, Teistler M, Pretschner DP (1999) Elastodynamic shape modeling in virtual medicine. In: Proceedings shape modeling international ’99. International conference on shape modeling and applications, Aizuwakamatsu, Japan, pp 172–178

  29. Taylor MJD, Beneke R (2012) Spring mass characteristics of the fastest men on earth. Int J Sports Med 33:667–670

    Article  Google Scholar 

  30. Wang HP, Mustafa GIY, Tian Y (2018) Model-free fractional-order sliding mode control for an active vehicle suspension system. Adv Eng Softw 115:452–461

    Article  Google Scholar 

  31. Yang J, Shang S (2013) Cloth modeling simulation based on mass spring model. Appl Mech Mater 310:676–683

    Article  Google Scholar 

  32. Yao S, Zhou X, Hu G (2008) Experimental study on negative mass effective mass in a 1d mass-spring system. New J Phys 10(4):1–4

    Article  Google Scholar 

  33. Zerbato D, Galvan S, Fiorini P (2007) Calibration of mass spring models for organ simulations. In: 2007 IEEE/RSJ international conference on intelligent robots and systems, San Diego, CA, USA, pp 370–375

  34. Zhang S, Gu L, Huang P, Xu J (2005) Real-time simulation of deformable soft tissue based on mass-spring and medial representation. In: Computer vision for biomedical image applications, a workshop of ICCV2005, LNCS 3875, pp 419–426

  35. Zhenfang C, Bing H (2012) Research of fast cloth simulation based on mass–spring model. In: National conference on information technology and computer science (CITCS 2012), Lanzhou, China

Download references

Funding

Larry Guan was supported by the University of Houston through an Undergraduate Research Fellowship.

Author information

Authors and Affiliations

  1. Institute of Mathematical Sciences and Physics, University of the Philippines Los Baños, Los Baños, Laguna, Philippines

    Neil Jerome A. Egarguin

  2. Department of Mathematics, University of Houston, Houston, TX, USA

    Larry Guan & Daniel Onofrei

Authors
  1. Neil Jerome A. Egarguin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Larry Guan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Daniel Onofrei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Neil Jerome A. Egarguin.

Ethics declarations

Conflict of interest

The authors do not have conflicts of interest or competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Egarguin, N.J.A., Guan, L. & Onofrei, D. Defect Characterization in a 1D Spring Mass System Using the Laplace and Z-Transforms. J. Vib. Eng. Technol. 10, 1121–1134 (2022). https://doi.org/10.1007/s42417-022-00433-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00433-y

Keywords

Search

Navigation