Skip to main content
SpringerLink
Log in

Dynamic Investigation of FRP Cracked Beam Using Neural Network Technique

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

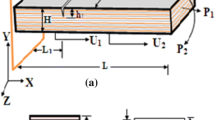
In the present investigation, vibration signatures have been used for identifying the place of crack and depth in pre-cracked FRP beams. Bidirectional (woven) FRP composite beams are consisting of 13 layers of epoxy–glass fibres (0°/7.5°/15°/22.5°/30°/37.5°/45°). Effects of clamped–free and clamped–clamped end conditions have been studied in the current investigation.

Methods

Fibre orientations effect on dynamics of FRP beam by the altering transverse crack location and its depth have been observed by applying analytical, finite element method, and neural network techniques.

Results

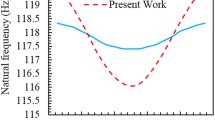
The results obtained have been verified experimentally. The outcomes of both methods have deviation within 6% during comparison.

Conclusion

From the investigation, it has been concluded that the natural frequencies and mode shapes can be used for identifying crack location and crack depth for different fibre orientation in FRP beam.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

A:

Cross-sectional area of the of FRP beam

C-F:

Clamp–free end condition

Cij :

Flexibility influence matrix

E:

Modulus of elasticity of the FRP beam material

FRP:

Fibre-reinforced plastic composite

F i (i = 1, 2):

Function determined experimentally

H :

Thickness of the beam

h 1 :

Pre-crack depth

I :

Moment of inertia

i, j :

Variables

J C :

Release rate of strain energy

K Ii (i = 1, 2):

Intensity factor of stress used for Pi load

K ij :

Local flexible element matrix

L :

Length of the FRP beam

L 1 :

Crack locale in FRP beam from one end

M i (i = 1, 4):

Compliance constant

P i (i = 1, 2):

Pi = axial force (i = 1) and Pj = bending load (i = 2)

K :

Stiffness matrix

u i (i = 1, 2):

Additional displacement functions

U c :

Strain energy caused by pre-crack

W :

FRP beam breadth

X, Y, and Z :

Reference co-ordinate for FRP beam

Y 0 :

Exciting vibration amplitude

y i (i = 1, 2):

Standard function (transverse) yi(x)

ω n :

Natural frequency of un-cracked FRP composite beam (NFUCB)

ω c :

Frequency of cracked FRP composite beam (FCCB)

∆ω :

(ωn) − (ωc)

(∆ω/ω n):

Relative eigen frequency (REF)

(ω c/ω n):

Relative natural frequency (RNF)

χ :

Relative crack depth (RCD = \(\frac{{h_{1} }}{H}\)) 

\(\psi\) :

Relative crack location (RCL = L1/L)

\(\rho_{\text{C}}\) :

FRP composite beam mass density

\(\delta \,\) :

Constant of characteristic equation

\(\varUpsilon\) :

Coefficient of independent force

\(g\) :

Complex constants

References

  1. ANSYS, released version 13, user manual

  2. Altun F, Dirikgil T (2013) The prediction of prismatic beam behaviors with polypropylene fiber addition under high temperature effect through ANN, ANFIS and fuzzy genetic models. Compos Part B Eng 52:362–371

    Article  Google Scholar 

  3. Cao M, Radzieński M, Xu W, Ostachowicz W (2014) Identification of multiple damage in beams based on robust curvature mode shapes. Mech Syst Sig Process 46:468–480

    Article  Google Scholar 

  4. Dash AK, Parhi DR (2011) A vibration based inverse hybrid intelligent method for structural health monitoring. Int J Mech Mater Eng 6(2):212–230

    Google Scholar 

  5. Fang X, Luo H, Tang J (2005) Structural damage detection using neural network with learning rate improvement. Comput Struct 83(25–26):2150–2161

    Article  Google Scholar 

  6. Ghoneam SM (1995) Dynamic analysis of open cracked laminated composite. Compos Struct 32:3–11

    Article  Google Scholar 

  7. Hagan MT, Demuth HB (1996) Neural network design, 1996. PWS publishing Company, a division of Thomson Learning, Boston

    Google Scholar 

  8. Jones RM (1999) Mechanics of composite materials, 2nd edn. Taylor and Francis, New York

    Google Scholar 

  9. Knibbs RH, Morris JB (1974) The effects of fiber orientation on the physical properties of composites. Composite 5:209–218

    Article  Google Scholar 

  10. Maiti A, Majumdar DK, Maity D (2012) Damage assessment of truss structures from changes in natural frequencies using ant colony optimization. Appl Math Comput 218:9759–9772

    MATH  Google Scholar 

  11. Nikpur K, Dimarogonas A (1988) Local of compliance of composite cracked bodies. Compos Sci Technol 32:209–223

    Article  Google Scholar 

  12. Nguyen SD, Ngo KN, Tran QT, Choi SB (2013) A new method for beam-damage-diagnosis using adaptive fuzzy neural structure and wavelet analysis. Mech Syst Sig Process 39:181–194

    Article  Google Scholar 

  13. Rafiee J, Tse PW, Harifi A, Sadeghi MH (2009) A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system. Expert Syst Appl 36(3):4862–4875

    Article  Google Scholar 

  14. Sekhar AS (2008) Multiple cracks effects and identification. Mech Syst Sig Process 22:845–878

    Article  Google Scholar 

  15. Suresh S, Omkar SN, Ganguli R, Mani V (2004) Identification of crack location and depth in a cantilever beam using a modular neural network approach. Smart Mater Struct 13(4):907–915

    Article  Google Scholar 

  16. Tada H, Paris PC, Irwin GR (1973) The stress analysis of cracks handbook. Del research Corporation, Hellertown

    Google Scholar 

  17. Vinson JR, Sierakowski RL (1991) Behaviour of structures composed of composite materials, 1st edn. Martinus Nijhoff, Dordrecht

    MATH  Google Scholar 

  18. Xue JN, Jiao XL, Xiao RY, Ji F (2012) Modal analysis of laminated composite beam based on elastic wave theory. Appl Mech Mater 151:275–280

    Article  Google Scholar 

  19. Zheng SJ, Li ZQ, Wang HT (2011) A genetic fuzzy radial basis function neural network for structural health monitoring of composite laminated beams. Expert Syst Appl 38(9):11837–11842

    Article  Google Scholar 

  20. Zhu F, Deng Z, Zhang J (2013) An integrated approach for structural damage identification using wavelet neuro-fuzzy model. Expert Syst Appl 40:7415–7427

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Production Engineering, Veer Surendra Sai University of Technology, Burla, Odisha, 768018, India

    Pankaj Charan Jena

  2. Department of Mechanical Engineering, N.I.T, Rourkela, Odisha, 769008, India

    Dayal R. Parhi

  3. Department of Mechanical Engineering, Jadavpur University, Jadavpur, Kolkata, 700032, India

    G. Pohit

Authors
  1. Pankaj Charan Jena
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dayal R. Parhi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. Pohit
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pankaj Charan Jena.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jena, P.C., Parhi, D.R. & Pohit, G. Dynamic Investigation of FRP Cracked Beam Using Neural Network Technique. J. Vib. Eng. Technol. 7, 647–661 (2019). https://doi.org/10.1007/s42417-019-00158-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-019-00158-5

Keywords

Search

Navigation