Skip to main content
SpringerLink
Log in

Parametric Stability Analysis of a Parabolic-Tapered Rotating Beam Under Variable Temperature Grade

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

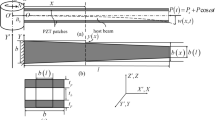
The static and dynamic stability of a parabolic-tapered beam of circular cross-section subjected to an axial alive load and rotating in the X-Y plane about the Z-axis is analyzed cosidering a variable temperature grade along the centroidal axis of the beam as the beam is in steady state condition.

Methods

The stability is analyzed for clamped-clamped and pinned-clamped boundary conditions. The parametric instability regions are acquired by means of Saito-Otomi conditions. The consequences of variation parameter, revolution speed, temperature grade and boundary conditions on the instability regions are examined for dynamic load and static buckling loads for 1st, 2nd and 3rd modes and are represented by a number of graphs.

Results

The results divulge that the stability is increased by increasing revolution speed; however, increase in thermal grade and the variation parameter leads to destabilize the converging system for all boundary conditions.

Conclusions

This research can be useful for vibration isolation of rotating non-uniform beams with high surrounding temperature and moderate rotational speeds and the design of rotor blades with high strength to weight ratio by choosing the suitable parameters obtained from this computational analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

\( A\left( x \right) \) :

Cross-sectional area of any standard segment

\( A (\eta ) \) :

Non-dimensional cross-sectional area of any standard segment

A :

Cross-sectional area of the base

\( \left( {a,0} \right) \) :

Location of the focus of the parabola

B 0 :

Radius of the hub

\( b_{0} \) :

Dimensionless hub radius (\( {{B_{0} } \mathord{\left/ {\vphantom {{B_{0} } l}} \right. \kern-0pt} l} \))

\( d\left( x \right) \) :

Diameter of any standard segment

\( d (\eta ) \) :

Non-dimensional diameter of any standard segment

\( d_{l} \) :

Diameter of the far end section

\( E\left( x \right) \) :

Young’s modulus at any standard segment

\( E \) :

Young’s modulus at the base

f :

Frequency of external excitation

\( \overline{f} \) :

Non-dimensional excitation frequency

\( I\left( x \right) \) :

Moment of inertia of any standard segment

\( I (\eta ) \) :

Non-dimensional moment of inertia

I :

Area moment of inertia of the base

l :

Span of the beam

\( m (\eta ) \) :

Mass variation function

N :

Angular speed about Z-axis

N 0 :

Revolution speed parameter

\( S (\eta ) \) :

Elastic modulus variation function

\( T (\eta ) \) :

Moment of inertia variation function

t :

Time

\( W_{0} \) :

Static load along axial direction

\( W_{1} \) :

Alive load along axial direction

\( w\left( \tau \right) \) :

Non-dimensional external load

\( w_{0} \) :

Non-dimensional static load along axial direction

\( w_{1} \) :

Dimension less axial alive load

\( \Delta \left( {x,t} \right) \) :

Deflection along the transverse direction

\( \psi \) :

Parameter for temperature grade

\( \psi (\eta ) \) :

Temperature grade or thermal gradient variation function

\( \alpha \) :

Coefficient of thermal expansion of the beam material

\( \beta^{*} \) :

Variation or taper parameter (\( = {a \mathord{\left/ {\vphantom {a D}} \right. \kern-0pt} D} \))

\( \gamma \) :

\( = {l \mathord{\left/ {\vphantom {l D}} \right. \kern-0pt} D} \)

\( \xi \) :

Dimensionless transverse displacement

\( \eta \) :

Non-dimensional length \( ({x \mathord{\left/ {\vphantom {x l}} \right. \kern-0pt} l} ) \)

\( \tau \) :

Dimensionless time

\( \rho \) :

Mass density of the beam material

\( \delta_{0} \) :

Reference temperature

\( \delta \) :

Temperature at the base

References

  1. Rao JS, Carnegie W (1970) Solution of the equation of motion of coupled bending-torsion vibration of turbine blades by the method of Ritz-Galerkin. Int J Mech Eng 12:875–882

    MATH  Google Scholar 

  2. Rao JS, Banerjee S (1977) Coupled bending-torsional vibration of cantilever blades- method of polynomial frequency equation. Mech Mach Theory 12:271–280

    Article  Google Scholar 

  3. Nirodson F (1954) Vibration of turbine blades with loose hinge supports. Eng Digest 15:359

    Google Scholar 

  4. Horway G (1948) Chord wise and beam wise bending frequencies of hinged rotor blades. J Aeronaut Sci 15:497–502

    Article  Google Scholar 

  5. Schilhansl MJ (1958) Bending frequency of a rotating cantilever beam. J Appl Mech ASME 25:28–30

    MathSciNet  MATH  Google Scholar 

  6. Yntema TR (1955) Simplified procedure and charts for the rapid estimation of bending frequencies of beams, NACA-TN-3459

  7. Dash PR, Pradhan M, Bisoi A (2016) Parametric stability of an asymmetric sandwich beam with thermal gradient under various boundary conditions by computational method. Proce Eng 144:900–907

    Article  Google Scholar 

  8. Rao JS, Carnegie W (1970) Nonlinear vibration of rotating cantilever beams. J R Aeronaut Soc 74:161

    Google Scholar 

  9. Carnegie W (1959) Vibration of rotating cantilever blading: theoretical approaches to the frequency problem based on energy methods. J Mech Eng Sci 1:235

    Article  MATH  Google Scholar 

  10. Carnegie W (1967) The application of the Variational method to derive the equations of motion of vibrating cantilever blading under rotation. Bull Mech Eng Educ 6:29

    Google Scholar 

  11. Pradhan M, Dash PR (2016) Stability of an asymmetric tapered sandwich beam resting on a variable Pasternak foundation subjected to a pulsating axial load and thermal gradient. Compos Struct 140:816–834

    Article  Google Scholar 

  12. Rao JS, Belgaumkar BM, Carnegie W (1970) Torsional vibration of a cantilever beam of rectangular cross section with uniform taper. Bull Mech Eng Educ 9:61

    Google Scholar 

  13. Kar RC, Sujata T (1988) Parametric instability of a non-uniform beam with thermal gradient resting on a Pasternak foundation. Comput Struct 29:591–599

    Article  MATH  Google Scholar 

  14. Nayak S, Bisoi A, Dash PR, Pradhan PK (2014) Static stability of a visco-elastically supported asymmetric sandwich beam with thermal gradient. Int J Adv Struct Eng 65:1–7

    Article  Google Scholar 

  15. Parida R, Dash PR (2016) Dynamic stability analysis of a circularly tapered rotating beam subjected to axial pulsating load and thermal gradient under various boundary conditions. Int J Acoust Vib 21:137–144

    Google Scholar 

  16. Ghosh R, Dash P, Dharmavaram Y, Pavan Kumar VVS, Ray K (2008) Parametric instability of a tapered, asymmetric, sandwich beam under various boundary conditions. Adv Vib Eng 7(1):71–89

    Google Scholar 

  17. Saito H, Otomi K (1979) Vibration and stability of elastically supported beams carrying an attached mass under axial and tangential loads. J Sound Vib 62:257–266

    Article  Google Scholar 

  18. Saito H, Otomi K (1979) Parametric response of visco-elastically supported beams. J Sound Vib 63:169–178

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, VSSUT, Burla, Sambalpur, Odisha, 768018, India

    R. R. Chand, P. K. Behera, M. Pradhan & P. R. Dash

Authors
  1. R. R. Chand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. K. Behera
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Pradhan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. P. R. Dash
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. R. Dash.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chand, R.R., Behera, P.K., Pradhan, M. et al. Parametric Stability Analysis of a Parabolic-Tapered Rotating Beam Under Variable Temperature Grade. J. Vib. Eng. Technol. 7, 23–31 (2019). https://doi.org/10.1007/s42417-018-0071-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-018-0071-y

Keywords

Search

Navigation