Wave Radiation from Bottom Vibrations in Open-Channel Flow with Uniform Vorticity

Abstract

The linearized water-wave radiation problem for a 2D oscillating source in an inviscid shear flow with a free surface is investigated analytically. The singular source is located at the bottom, with constant fluid depth. The velocity of the basic flow varies linearly with depth, assuming uniform vorticity. The far-field surface waves radiated out from the 2D bottom source are calculated, based on Euler’s equation of motion with the application of radiation conditions. The present analysis extends the work by Tyvand and Sveen to include a nonzero surface flow. Doppler effects will arise in a system at rest with the undisturbed free surface. Resonance with zero group velocity will occur at a critical Froude number for the surface flow. In the presence of a basic surface flow, there are in total four radiated waves when the surface flow is subcritical. With supercritical flow, there are only two emitted waves, with downstream propagation. The critical Froude number depends on the surface velocity, the shear rate and the oscillation frequency of the bottom source.

1 Introduction

An elementary solution for linearized water waves is constituted by the submerged oscillatory source. Oscillatory sources serve to provide Green functions for Laplace’s equation, obeying the linearized free-surface condition and radiation conditions at infinity. Kochin [9] gave the first versions of these singular solutions relevant for water waves interacting with submerged and floating bodies. See the review article by Wehausen and Laitone [15] and the books by Newman [10] and Faltinsen [8].

The present flow problem will give a fundamental singular solution for a rotational unidirectional open-channel flow with bottom vibrations. We will give the basis for a Green function formalism of water wave radiation in two dimensions by considering one singular point of bottom oscillations, which is equivalent to an oscillatory Dirac singularity for the normal velocity. The work by Tyvand and Torheim [14] with uniform basic flow will here be extended to include a constant vorticity. For the actual formulation of a Green function integral we refer to this previous work. Section 3 in [14] demonstrated the formulation of a Green function integral for radiated waves from an arbitrary distribution of monochromatic bottom vibrations.

The exact dispersive theory of linearized water waves is applied, while the conventional theories of open-channel hydraulics are restricted to shallow-water approximations. The present assumption of 2D waves is adequate for waves in straight open channels, where the ratio of wavelength to channel width is of order one or greater.

Our solution will be based on the Euler equation of motion for an incompressible inviscid fluid. The amplitudes of the radiated far-field waves will be calculated analytically. The present inclusion of a surface flow extends the previous work by Tyvand and Sveen [13], who studied shear flow with zero surface velocity, where there are always two waves radiated out to infinity. One upstream wave and one downstream wave, which correspond to the two regular waves discussed by Ellingsen and Tyvand [7]. They studied a submerged oscillatory source which generates perturbation vorticity carried with the flow as a third wave severely influencing the two regular waves. Our model of an oscillatory source placed at the bottom is simpler, since Lord Kelvin’s circulation theorem does not allow any perturbation vorticity to be generated in the fluid. The analysis by Ellingsen and Tyvand [7] showed that a submerged oscillating source in a shear flow cannot provide a Green function for linearized water waves, because of the disturbing influence of the source. It gives a critical-layer like behavior for the perturbation vorticity, inducing a surface disturbance which is not a gravitational wave. This undulating disturbance of perturbation vorticity is not a gravitational wave because it is not governed by the dispersion relation. It is propagated by the shear flow, with its velocity at the location of the source.

Our previous model [13] with only subsurface basic flow is quite transparent physically. With the present inclusion of a nonzero surface velocity, the situation is considerably more complicated. Because of Doppler effects, there may be up to four radiated waves. Two of these waves will have upstream phase velocity, and when these two waves merge, there is resonance with zero group velocity and infinite wave amplitude, according to linear theory [14]. In the present work, the subcritical resonance and the dependencies of the radiated wave and its frequency will be investigated, for given flow parameters, which is the Froude number and the shear rate.

Similar to the work by Tyvand and Torheim [14] we expect four different waves to be radiated at subcritical Froude numbers. The previous model [14] was the same as the present one, but without vorticity in the (uniform) basic flow. A first and a second wave was found to propagate in the downstream direction. At the critical Froude number, the third and fourth wave merge, as a resonant case with zero group velocity and diverging amplitude according to linear theory. Nonlinear theory is required to study finite-amplitude resonant waves, and this has been done by Bestehorn and Tyvand [1] for the same physical problem as [14]. This fully nonlinear free-surface problem lead to finite wave amplitude at all frequencies. The numerical results by Bestehorn and Tyvand [1] showed that the highest wave peaks occurred for Froude numbers slightly below the critical value of resonance at a given frequency. The first nonlinear analysis of this type of resonance was performed by Dagan and Miloh [4], for a 2D submerged oscillating source in a uniform basic flow.

The review article by Peregrine [11] revealed a limited amount of work on fully dispersive water waves on shear flow. The focus of this research remains on ocean wave drift and weakly nonlinear interactions. Brevik [2] studied the possibilities of stopping a surface wave by generating a shear flow. Ellingsen and Brevik [6] gave a detailed discussion of the dispersion relation for linear waves, and Ellingsen [5] applied these results to study ship-waves on a shear flow. The present work follows up the paper by Ellingsen and Tyvand [7] on an oscillatory line source submerged in a shear flow with a free surface. The focus was on infinite depth, and only the case of vanishing surface flow was treated. In the present work we will consider an oscillating bottom source, which is equivalent to a singular flux through the bottom, oscillating harmonically in time.

We will consider a bottom source, which is simpler than a submerged source, because there is no generation of vorticity in the fluid domain. We include a nonzero surface velocity, which will induce Doppler effects, possibly resulting in four different waves being emitted from the oscillating source, for certain ranges of the parameter choices.

2 Mathematical Model

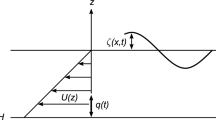
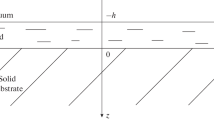
We consider an inviscid and incompressible fluid (liquid) in a steady shear flow, where the shear flow is aligned along a horizontal x-axis. In addition there is a uniform horizontal flow with an arbitrary direction. The fluid has constant depth H and a free surface subject to constant atmospheric pressure. Surface tension is neglected. Cartesian coordinates x, z are introduced, where the z-axis is directed upwards in the gravity field and the x-axis is aligned along the undisturbed free surface. The gravitational acceleration is g, and $\rho$ denotes the constant fluid density. The velocity perturbation vector is denoted by $({\hat{u}},{\hat{w}})$.

The surface elevation is denoted by $\zeta (x, t)$, see the sketch in Fig. 1. There is a wave motion caused by a fixed oscillating line source (2D source) located in the bottom point $(0,-H)$. The angular frequency $\omega$ of this forced bottom source is given. The water wave problem will be linearized with respect to the surface elevation and the velocity perturbation.

Fig. 1

Definition sketch for the oscillating bottom source q(t), the linearly varying basic flow U(z), and the free-surface elevation $z=\zeta (x,t)$. The fluid layer has constant depth H. This figure illustrates the flow with a positive value for the velocity S

There is a basic horizontal shear flow U(z) in the x direction

$$\begin{aligned} U(z) = U_0 + S z,\quad z <0, \end{aligned}$$

(1)

where $U_0$ is the uniform surface velocity, which is defined nonnegative. There is a uniform vorticity S in the $-y$ direction. When $U_0>0$, there is no restriction concerning the sign of S, and the x-axis points in the downstream direction of the surface flow.

When $U_0=0$, we choose to make the restriction $S \ge 0$, which means that the x-axis points in the upstream direction of the subsurface flow, in the absence of a surface flow.

Euler’s equation of motion can be written

$$\begin{aligned} {\vec {a}} = - \frac{1}{\rho } \nabla P - g {\vec {i}}_z, \end{aligned}$$

(2)

where ${\vec {a}}$ is the acceleration vector and ${\vec {i}}_z$ is the vertical unit vector. The total pressure is denoted by P. The mass balance is given by the continuity equation

$$\begin{aligned} {\hat{u}}_x + {\hat{w}}_z = 0. \end{aligned}$$

(3)

The linearized kinematic free-surface condition is

$$\begin{aligned} \left. {\hat{w}} \right| _{z=0} = \zeta _t + U_0 \zeta _x, \end{aligned}$$

(4)

with subscripts denoting partial derivatives.

Surface tension is neglected, and the dynamic boundary condition is given by the tangential component of the Euler equation along the free surface. It can be written

$$\begin{aligned} {\vec {a}} - ({\vec {a}}\cdot {\vec {n}}){\vec {n}} = - g \vec {i_z} + g (\vec {i_z}\cdot {\vec {n}}){\vec {n}},\quad z=\zeta (x,y,t), \end{aligned}$$

(5)

where the surface normal vector is denoted by ${\vec {n}}$. According to linear theory, the surface normal is given by ${\vec {n}}={\vec {i}}_z-\nabla \zeta$. We linearize this dynamic free-surface condition and take its x component, which gives

$$\begin{aligned} {\hat{u}}_t + U_0 {\hat{u}}_x + S {\hat{w}} = - g \zeta _x,\quad z=0. \end{aligned}$$

(6)

Ellingsen and Tyvand [7] assumed $U_0 = 0$, while we can generalize their analysis by the transformation

$$\begin{aligned} \frac{\partial }{\partial t} \rightarrow \frac{\partial }{\partial t} + U_ 0 \frac{\partial }{\partial x}, \end{aligned}$$

(7)

to get a free-surface condition expressed by the vertical velocity alone

$$\begin{aligned} \left( \frac{\partial }{\partial t} + U_0 \frac{\partial }{\partial x}\right) ^2 {\hat{w}}_{z} - S \left( \frac{\partial }{\partial t} + U_0 \frac{\partial }{\partial x}\right) {\hat{w}}_{x} = g {\hat{w}}_{xx},\quad z=0. \end{aligned}$$

(8)

Our bottom condition represents a singular oscillating source located in a fixed bottom point

$$\begin{aligned} {\hat{w}} = q_0 \delta (x) {\textrm{e}}^{-i \omega t},\quad z=-H, \end{aligned}$$

(9)

where $q_0$ is the flux amplitude of the bottom source, given in 2D as area per time. The Dirac delta function is denoted by $\delta (x)$, and i is the imaginary unit. We have introduced a complex time dependence with angular frequency $\omega$. The physical quantities are represented by the real parts of the complex variables.

The singular condition (9) allows the construction of a Green function for linearized water waves emitted from bottom vibrations. It may serve as the building block for expressing an arbitrary distribution of monochromatic oscillation along a finite portion of the bottom. In [14], it was shown how to construct such a Green function integral.

3 Fourier Transform of the Radiation Problem

The flow is assumed driven by a bottom source of harmonically pulsating strength

$$\begin{aligned} q(t) = q_0 \cos (\omega t). \end{aligned}$$

(10)

This is the physical source but it needs to be expressed mathematically as a complex exponential function, to allow water waves that are radiated both in the upstream and downstream directions. The sign of the wave number k in the Fourier integral will then represent the direction of wave propagation. The variables can now be Fourier transformed as follows:

$$\begin{aligned} ({\hat{u}},{\hat{w}},{\hat{p}}) = q_0 \frac{1}{2 \pi } \int _{-\infty }^{\infty } (u(z),w(z),p(z)) {\textrm{e}}^{i k x - i \omega t} {\textrm{d}}k. \end{aligned}$$

(11)

This Fourier integral consists of two different contributions: Waves propagating in the $+x$ direction, with positive wavenumber $(k>0).$ Waves propagating in the $-x$ direction, with negative wavenumber $(k<0).$

The transformed components of the Euler equation are given by

$$\begin{aligned} - i (\omega - k U) u + S w= & {} - i k p/\rho , \end{aligned}$$

(12)

$$\begin{aligned} - i (\omega - k U) w= & {} - p'/\rho , \end{aligned}$$

(13)

where the derivative is taken with respect to z. The transformed continuity equation is

$$\begin{aligned} i k u + w' = 0. \end{aligned}$$

(14)

The surface elevation is Fourier transformed as follows:

$$\begin{aligned} \zeta (x,t) = q_0 \frac{1}{2 \pi } \int _{-\infty }^{\infty } B(\omega ,k) {\textrm{e}}^{i k x - i \omega t} {\textrm{d}}k. \end{aligned}$$

(15)

We derive an equation for the vertical velocity alone

$$\begin{aligned} w'' - k^2 w = 0. \end{aligned}$$

(16)

The transformed bottom condition (9) is

$$\begin{aligned} w = 1,\quad z=-H. \end{aligned}$$

(17)

The solution of this second-order boundary value problem is

$$\begin{aligned} w(z) = \cosh k(z+h) + A \sinh k(z+h). \end{aligned}$$

(18)

The Fourier transform (11) involves the whole spectrum of positive and negative wave numbers k. We introduce a modified angular frequency $\Omega = \omega - k U_0$. The transformed kinematic free-surface condition (4) is

$$\begin{aligned} w\vert _{z=0} = -i \Omega B. \end{aligned}$$

(19)

We insert the solution (18) to find

$$\begin{aligned} \cosh kh + A \sinh kh = -i \Omega B. \end{aligned}$$

(20)

Similarly, the transformed dynamic free-surface condition (6) is

$$\begin{aligned} (-i \Omega u + S w)\vert _{z=0} = \left. \left( \frac{\Omega }{k} w' + S w\right) \right| _{z=0} = - i k g B, \end{aligned}$$

(21)

where the solution for w leads to another link between A and B

$$\begin{aligned} \Omega \sinh kh + S \cosh kh + A (\Omega \cosh kh + S \sinh kh ) = - i k g B. \end{aligned}$$

(22)

We eliminate A from these two relationships to solve for $B(\Omega )$

$$\begin{aligned} B = i~\frac{\Omega }{\sinh kh}~\frac{1}{\Omega ^2 \coth kh + {\Omega } S - g k}. \end{aligned}$$

(23)

4 Waves with Surface Velocity $U_0 > 0$

In our previous paper [13], we solved the present radiation problem for the special case of vanishing surface flow $(U_0 = 0).$

With this background, we proceed further to solve the radiation problem with surface flow, defined positive $(U_0 > 0)$. Then we reintroduce $\omega$ in the above formulas $(\Omega =\omega - k U_0).$ The vorticity S can now have any value, not restricted to be positive. The upstream $(x<0)$ and downstream $(x>0)$ directions are now dictated by the direction of the surface velocity $U_0$.

We introduce dimensionless variables, based on the depth H as length unit, combined with a gravitational time unit $\sqrt{H/g}$. These are

$$\begin{aligned} \omega ^* = \sqrt{\frac{H}{g}} \omega ,\quad S^* = \sqrt{\frac{H}{g}} S,\quad k^* = k H, \end{aligned}$$

(24)

being the given dimensionless source frequency $\omega ^*$, the dimensionless vorticity $S^*$ and the source-induced upstream/downstream dimensionless wave numbers $k^*$ of radiated waves, respectively. As we have a positive surface velocity $U_0$, we introduce the Froude number F for the surface flow

$$\begin{aligned} F = \frac{U_0}{\sqrt{g H}}, \end{aligned}$$

(25)

where $F>0$ by definition, while the shear rate $S^*$ may be positive or negative. The dimensionless dispersion relation is thus given by the common equation for $k^* (\omega ^*, S^*, F)$. The modified angular frequency $\Omega = \omega - k U_0$ will have the dimensionless version $\Omega ^* = \omega ^* - k^* F$.

There can be up to four different radiated waves, and we introduce subscripts 1, 2, 3, 4 for these possible four waves. Their properties will be discussed below. The dispersion relation with these classes of waves has been discussed by Tyvand and Lepperød [12], but only for infinite depth. Finite depth is essential in the present paper because the source is placed at the bottom, so we take the depth H as our length unit.

4.1 The Dispersion Relation with Surface Flow

The dimensionless dispersion relation is given by the common implicit equation for determining $k_{1,2,3,4}^* (\omega ^*, S^*, F)$

$$\begin{aligned} k^* = (\omega ^* - k^* F)^2 \coth k^* + (\omega ^* - k^* F) S^* . \end{aligned}$$

(26)

Figures 2, 3 and 4 illustrate the multi-valued dispersion relation $k^*(\omega ^*)$ for different choices of F and $S^*$. Figure 2 shows a Froude number $F=0.25$ in combination with a shear rate $S^* = \pm 0.5$, adding the reference case of uniform flow $S^*=0$ [12]. Figure 3 shows the higher Froude number $F=0.5$, with three choices for the shear flow: $S^* = \pm 0.25$ and the reference case $S^* = 0$.

Fig. 2

The multi-valued dispersion relation $|k^*(\omega ^*)|$ with Froude number $F=0.25$. Three different shear rates are displayed: Dotted curves represent $S^* = 0$ (uniform flow). Solid curves represent $S^*=0.5$. Dashed curves represent $S^* =- 0.5$. The positive (downstream) wave numbers $k_{1}^*$ and $k_{2}^*$ are given by the lower and upper monotonous curves, respectively. The intermediate (double-valued) curves represent the two waves with negative wave numbers $k_{3}^*$ and $k_{4}^*$. These waves with upstream phase velocity merge at resonance, where $\omega ^*$. $k_{3}^*$ is the smallest and $k_{4}^*$ is the greatest of the two wave numbers for these sub-resonant waves

Fig. 3

The multi-valued dimensionless dispersion relation $|k^*(\omega ^*)|$ for an oscillating bottom source in a flow with Froude number $F=0.5$. Three different shear rates are displayed: Dotted curves represent $S^*= 0$ (uniform flow). Solid curves represent $S^*=0.25$. Dashed curves represent $S^*=- 0.25$. The positive (downstream) wave numbers $k_{1}^*$ and $k_{2}^*$, given by the lower and upper monotonous curves, exist for all frequencies $\omega ^*>0$. The intermediate (double-valued) curves represent the two waves with negative wave numbers $k_{3}^*$ and $k_{4}^*$ (having upstream phase velocities). These waves merge at resonance, where $\omega ^*$ has its maximum admissible value for these waves to exist. The smallest value is $k_{3}^*$ and the greatest value $k_{4}^*$ for the two wave numbers of waves that exist only for subresonant frequencies

Fig. 4

The double-valued dispersion relation $|k^*(\omega ^*)|$ with supercritical Froude number $F=1.2$. Three different shear rates are displayed: Dotted curves represent $S^*=0$ (uniform flow). Solid curves represent $S*=0.1$. Dashed curves represent $S^*=- 0.1$. The positive (downstream) wave numbers $k_{1}^*$ and $k_{2}^*$ are given by the lower and upper monotonous curves, respectively. These two waves are the only ones. No resonance is possible, and there are no radiated upstream waves

Figures 2 and 3 represent subcritical Froude numbers where four different waves may be radiated from the oscillating source. We therefore add Fig. 4 where only two different waves are radiated. This is achieved by choosing a supercritical Froude number $F=1.2$, combined with the shear rates $S^* = \pm 0.1$ and $S^* = 0$.

Figures 2 and 3 represent subcritical flow with the richest dispersion relation (26) having four different waves generated for a given angular frequency $\omega ^* > 0$, with a basic flow $F > 0$. We solve the radiation problem in the coordinate system at rest with the source. Thereby the wave problem remains monochromatic, with the given frequency of forced source oscillation as the only frequency. If we changed the coordinate system to be at rest with the undisturbed free surface, there would be explicit Doppler effects for the surface waves, where they would have frequencies different from the source frequency. The only convenient mathematical procedure is to keep the problem monochromatic, whereby the Doppler effects remain hidden, but they would emerge if we described the wave from a coordinate system at rest with the undisturbed free surface.

The first wave exists for all parameter values and is the downstream wave with the longest wavelength, so that its wavenumber $k^*_1$ is the smallest positive solution for $k^*$ in the dispersion relation. The conventional way of expressing the dispersion relation for this longest downstream wave with positive wave number is as follows

$$\begin{aligned} \omega ^* = F k_1^* + \frac{\tanh k_1^*}{2} \left( - S^* + \sqrt{ (S^*)^2 + 4 k_1^* \coth k_1^*}\right) , \end{aligned}$$

(27)

leading to the dimensionless phase velocity $c_f^* = \omega ^*/k_1^*$ and the more complicated dimensionless group velocity

$$\begin{aligned} c_g^* = F + \frac{1 - 2 k_1^* ~\text{ csch }~ (2 k_1^*)}{\sqrt{ (S^*)^2 + 4 k_1^* \coth k_1^*}} + \frac{\text{ sech}^2 k_1^*}{2} \left( - S^* + \sqrt{ (S^*)^2 + 4 k_1^* \coth k_1^*}\right) . \end{aligned}$$

(28)

These formulas are valid for the first wave with dimensionless wavenumber $k_1^*$. This is a long wave that has both phase and group velocity in the downstream direction $x \rightarrow \infty$.

The other wave with downstream phase velocity has positive wave number $k_2$, with the dispersion relation

$$\begin{aligned} \omega ^* = F k_2^* - \frac{\tanh k_2^*}{2} \left( S^* + \sqrt{ (S^*)^2 + 4 k_2^* \coth k_2^*}\right) , \end{aligned}$$

(29)

leading to the dimensionless phase velocity $c_f^* = \omega ^*/k_2^*$ and the more complicated dimensionless group velocity

$$\begin{aligned} c_g^* = F - \frac{1 - 2 k_2^* ~\text{ csch }~ (2 k_2^*)}{\sqrt{ (S^*)^2 + 4 k_2^* \coth k_2^*}} - \frac{\text{ sech}^2 k_2^*}{2} \left( S^* + \sqrt{ (S^*)^2 + 4 k_2^* \coth k_2^*}\right) .\nonumber \\ \end{aligned}$$

(30)

The dispersion relation for the third and fourth waves with upstream phase velocity (having negative wave numbers) is

$$\begin{aligned} \omega ^* = F k_j^* - \frac{\tanh k_j^*}{2} \left( S^* + \sqrt{ (S^*)^2 + 4 k_j^* \coth k_j^*}\right) ,\quad (j=3,4), \end{aligned}$$

(31)

leading to the dimensionless phase velocity $c_f^* = \omega ^*/k_j^*$ and the dimensionless group velocity

$$\begin{aligned} c_g^* = F - \frac{1 - 2 k_j^* ~\text{ csch }~ (2 k_j^*)}{\sqrt{ (S^*)^2 + 4 k_j^* \coth k_j^*}} - \frac{\text{ sech}^2 k_j^*}{2} \left( S^* + \sqrt{ (S^*)^2 + 4 k_j^* \coth k_j^*}\right) ,\quad (j=3,4).\nonumber \\ \end{aligned}$$

(32)

We note that these formulas are the same as those for the second wave, which has a positive wavenumber. The third and fourth wave have negative wavenumbers. By definition $\vert k_4 \vert > \vert k_3 \vert$.

The first and second waves are the waves that have phase velocities in the downstream direction $(x \rightarrow \infty ).$ The third and fourth wave are the waves that have phase velocities in the upstream direction $(x \rightarrow - \infty ),$ seemingly propagating against the surface flow. However, only the third wave will have upstream energy propagation, which means upstream group velocity. The fourth wave has a group velocity in the downstream direction, which means that its energy propagation is in the opposite direction of its phase velocity. This is important for applying the correct radiation condition in solving the mathematical problem for the emitted far-field waves.

4.2 On Resonance with Zero Group Velocity

The third and fourth wave will not exist if the Froude number is too large for a given source frequency, since the waves cannot propagate in the upstream direction if their opposing current is too strong. The threshold value for the Froude number that allows upstream wave propagation is called the critical Froude number $F_c$. It depends on the angular frequency $\omega ^*$ and the shear rate $S^*$. At the critical Froude number, the third and fourth wave will merge into one common wave with zero group velocity. This is resonance, for which the radiated wave amplitude is infinite according to linear theory with a strictly harmonic time dependence.

There are two possible ways of achieving finite wave amplitude at resonance: (i) To turn on the oscillating source at time zero and solve the linearized transient wave radiation problem. (ii) To take into account the fully nonlinear free-surface conditions. A full analysis of resonance will be to combine the free-surface nonlinearity with transient wave propagation from a source that is turned on at time zero. Dagan and Miloh [4] studied this nonlinear wave resonance from an oscillating submerged source with uniform flow at infinite depth. Only a small number of papers have appeared later. Understanding of linear theory with shear flow is necessary before attempting a nonlinear theory of resonance.

The present paper will be restricted to linear theory, with a strictly oscillatory source strength. A resonance will reveal itself by zero group velocity and infinite wave amplitude. It should be noted that the phase velocity at resonance is finite, and it is directed in the upstream direction. This is the common phase velocity of the merged third and fourth wave at resonance, where their joint group velocity is zero.

At resonance, there is a critical Froude number $F_c$ and an associated critical wave number $k_c^*$. We prefer to calculate the wave number by eliminating F from the Eqs. (31) and (32) to get the relationship

$$\begin{aligned} \omega ^*= & {} \frac{\tanh k_c^*}{2} \left( - S^* - \sqrt{ (S^*)^2 + 4 k_c^* \coth k_c^*} \right) \nonumber \\{} & {} + k_c^* \frac{1 - 2 k_c^* ~\text{ csch } (2 k_c^*)}{\sqrt{ (S^*)^2 + 4 k_c^* \coth k_c^*}} + \frac{k_c^*}{2}\text{ sech}^2 k_c^* \left( S^* + \sqrt{ (S^*)^2 + 4 k_c^* \coth k_c^*}\right) , \end{aligned}$$

(33)

valid at resonance where $c_g^*=0$ and $F=F_c$.

This equation is solved numerically with respect to the critical wave number $k_c^*(\omega ^*,S^*)$, which is the common wave number of the merged third and fourth wave at resonance. Table 1 shows numerical results for the critical wave number $k_c^*$ as a function of $\omega ^*$ and $S^*$. Tables 1, 2, 3 and 4 will focus exclusively on the parameter values (with given frequency) where there is a critical wave with resonance. With this restrictive constraint, these tables nevertheless cover a much broader range of parameter values for $S^*$ than the figures, where we have only displayed values of $S^*$ sufficiently small to avoid too great differences compared with uniform flow without vorticity [14].

After $k_c^*$ has been computed for a choice of values $\omega ^*$ and $S^*$, we can compute the critical Froude number from the formula

$$\begin{aligned} F_c = \frac{\omega ^*}{k_c^*} + \frac{\tanh k_c^*}{2 k_c^*} \left( S^* + {\sqrt{ (S^*)^2 + 4 k_c^* \coth k_c^*}} \right) . \end{aligned}$$

(34)

The critical Froude number $F_c(\omega ^*, S^*)$ where the group velocity of the third and fourth wave is zero, is tabulated in Table 2. For given parameters $\omega ^*$ and $S^*$, the third and fourth wave do not exist when $F>F_c$, while both of these waves exist for $0<F<F_c$, and they merge into a common critical wave at $F=F_c$.

Table 1 The absolute value of the (negative) critical wave number $\vert k_c^* \vert$ for the merged third and fourth wave at their joint resonance with zero group velocity

Table 2 The critical Froude number $F_c$ tabulated as a function of the shear rate $S^*$ and the angular frequency $\omega ^*$ of the source

Table 3 The far-field elevation amplitude $\vert \zeta _0^*\vert$ for the non-resonant first and second wave at resonance (where $F = F_c$) as functions of the shear rate $S^*$ and the angular frequency $\omega ^*$ of the source

Table 4 The wave numbers for the non-resonant first and second wave at resonance (where $F = F_c$) as functions of the shear rate $S^*$ and the angular frequency $\omega ^*$ of the source

The dispersion relation with infinite depth was studied by Tyvand and Lepperød [12]. The resonance condition with infinite depth defines the asymptotically valid critical Froude number $F_\infty$ by the relationship

$$\begin{aligned} 4 \omega ^* F_\infty = (1 + S^* F_\infty )^2, \end{aligned}$$

(35)

with the restriction on the shear rate $\vert S^* \vert < F^{-1}$. There is no deep-water resonance when $\vert S^* \vert > F^{-1}$. In our depth-based dimensionless representation, this asymptotic limit (35) must be interpreted as a high-frequency limit. The associated critical wave number with infinite depth is

$$\begin{aligned} k_c^* = \frac{F_\infty ^{-2} - (S^*)^2}{4}, \end{aligned}$$

(36)

in terms of the present dimensionless variables. From Eq. (35), we reproduce the resonance criterion in the absence of a shear flow $(S=0)$

$$\begin{aligned} \omega ^* F_\infty = \left( \frac{\omega U_0}{g}\right) _{\textrm{critical}} = \frac{1}{4}, \end{aligned}$$

(37)

which is the classical resonance at infinite depth [4].

We have now studied resonance on the basis of the dispersion relation. We will proceed to solve the radiation problem and derive the far-field wave amplitudes. With $\omega$ and $S^*$ given, we expect to find infinite wave amplitude at resonance, where the Froude number is $F=F_c$ and the wave number is $k_3^*=k_4^* = k_c^*$.

4.3 The Radiated Waves with Nonzero Surface Flow

The general Fourier integral solution for the surface elevation is given by (15)

$$\begin{aligned} \zeta (x,t) = q_0 \frac{1}{2 \pi } \int _{-\infty }^{\infty } B(\omega ,k) {\textrm{e}}^{i k x - i \omega t} {\textrm{d}}k \end{aligned}$$

(38)

and we can evaluate it by inserting from Eq. (23)

$$\begin{aligned} B = i~\frac{\omega - k U_0}{\sinh kh}~\frac{1}{(\omega - k U_0)^2 \coth kh + (\omega - k U_0) S - g k}, \end{aligned}$$

(39)

after substituting $\Omega = \omega - k U_0$.

There are four possible radiated waves with wavenumbers $k_j,(j=1,2,3,4)$, and we give a condensed common procedure for calculating their far-field amplitudes. Each separate far-field wave $(\vert x \vert \rightarrow \infty )$ can be written as

$$\begin{aligned} \zeta ^{(j)}(x,t) = \mp q_0 ~\frac{\omega - k_j U_0}{\sinh k_j h} {\textrm{e}}^{i k_j x - i \omega t} \lim _{k \rightarrow k_j}\frac{k - k_j}{(\omega - k U_0)^2 \coth kh + (\omega - k U_0) S - g k}.\nonumber \\ \end{aligned}$$

(40)

Here the minus sign refers to the integral being closed in the upper part of the complex k plane, while the plus sign refers to the integral being closed in the lower part of the complex k plane. By applying L’Hôpital’s rule to Eq. (40) we find

$$\begin{aligned}{} & {} \zeta ^{(j)}(x,t)\nonumber \\{} & {} \quad =\pm \frac{q_0 (\omega - k_j U_0) {\textrm{e}}^{i k_j x - i \omega t} }{(S U_0 + g) \sinh (k_j h) + 2 U_0 (\omega - k_j U_0) \cosh (k_j h) + h (\omega - k U_0)^2 \text{ csch } (k_j h)},\qquad \qquad \end{aligned}$$

(41)

which is valid separately for each of the waves $(j = 1,2,3,4)$ in their domains of existence, provided the correct sign in front of this formula is selected. The upper plus sign on the right hand side applies to the first, second and fourth wave. The lower minus sign on the right hand side applies to the third wave, since it is the only wave that is radiated in the $-x$ direction. From the dispersion relation we determine the integration path that picks the sign for each of these four different waves. We note that the shear rate S has an explicit influence on the wave amplitudes, which we saw was not the case in the absence of a surface flow $(F = 0).$

The critical wave at resonance is the joint upper limit for the domain of existence of the third and fourth wave. There are two different ways of looking at the combination $k_c(\omega ^*,S^*),~F_c(\omega ^*,S^*)$ as the upper limit for the third and fourth wave. (i) If we fix these parameters ($\omega ^*$ and $S^*$, while F is increased above $F_c$, the third and fourth wave will have a cut-off at the critical Froude number $F=F_c$. At the cut-off they merge into one joint wave with critical frequency and zero group velocity. (ii) If we instead keep F, $k^*$ and $S^*$ fixed but increase $\omega ^*$ beyond its value at resonance, the third and fourth wave will cease to exist. The critical wave can thus be viewed as either the marginal wave for upstream propagation at the strongest possible surface current (represented by the Froude number), or as the highest possible frequency for achieving upstream wave radiation at a given Froude number. We will see that the parameter range available for radiating upstream waves is very limited when $F>1$, since this may only happen for $S^*>0$. It is much easier to emit waves propagating to infinity in the downstream direction. In general, at least two downstream waves will always exist, and these are the first and the second wave.

The dimensionless version of the wave amplitude derived in Eq. (41) is

$$\begin{aligned} \vert \zeta _0^* \vert = \left| \frac{\omega ^* - k^* F }{(S^* F + 1) \sinh k^* + 2 F (\omega ^* - k^* F) \cosh k^* + (\omega ^* - k^* F)^2~ \text{ csch }~ k^*}\right| , \end{aligned}$$

(42)

and it is valid for all the four waves, in their domains of existence.

The obstacle for achieving a general overview of this radiation problem, is the complexity of the dispersion relation. The key to understanding the dispersion relation is the critical Froude number $F_c$, since the number of radiated waves depends on whether F is smaller than or greater than $F_c$. Above we have shown how $F_c$ varies with $\omega ^*$ and $S^*$.

In Table 2 the Froude number $F_c$ for resonance has been tabulated as a function of $\omega ^*$ and $S^*$. With this value $F_c$ for the Froude number, the elevation amplitudes $\zeta _0$ for the non-resonant first and second wave according to Eq. (42) are tabulated in Table 3. The corresponding wave numbers for the non-resonant waves are tabulated in Table 4.

From numerical studies of nonlinear resonance [1] we know that it is challenging to extract the different wave components, while the non-resonant waves may or may not obey linearized theory. Linear theory will be useful for identifying the wavenumbers of these non-resonant waves, tabulated in Table 4. Table 3 is less reliable for predicting the far-field amplitudes of these waves, but it will be important if we search for parameter ranges where one of the non-resonant waves may possibly become negligible. In [1] such precise values for the wavenumbers and radiation amplitudes of the non-resonant waves were useful for planning and interpreting the fully nonlinear computations. With this background, we consider Tables 1, 2, 3 and 4 to be a resource for fully nonlinear theories of radiation of water waves with resonance on a shear flow. We do not discuss these tables further here, because the behavior of non-resonant waves at the critical Froude number (assuming the frequency given) is not a central theme of the general linearized problem, where all the different waves are explicitly separated from one another. This is not the case in fully nonlinear theory, where the total wave with all its intermingled constituents can be computed. The tabulated non-resonant waves at the critical Froude number will then become important, in contrast to the peripheral role of these waves in a strictly linear theory.

The general formula (42) represents all the far-field amplitudes of the radiated waves. Figure 5 shows computations for these wave amplitudes for a supercritical Froude number $F=1.2$, accompanying the corresponding dispersion relation in Fig. 4. Only the first and second waves exist, and both of them are radiated in the downstream direction. The chosen shear rates $S^* = \pm 0.1$ in this figure are known from Fig. 4 to have only small influence on the dispersion relation. The case of zero shear flow is included with dots both in Figs. 4 and 5.

Fig. 5

The dimensionless far-field elevation amplitude $|\zeta _{0}^*|$ of the radiated waves, as function of the dimensionless wave number $|k^*|$, for three different shear rates. A supercritical value $F=1.2$ is chosen for the Froude number, so there are only two radiated waves. This figure shows the same case as Fig. 4. Dotted curves represent $S^*=0$ (uniform flow). Solid curves represent $S^*=0.1$. Dashed curves represent $S^*=- 0.1$. The three closely spaced (blue) curves represent 10 $|\zeta _{1}^*(k_{1})|$ for the first (the longer downstream) wave. The three other curves (brown) represent $|\zeta _{2}^*(k_{2})|$ for the second (the shorter downstream) wave

Figure 6 represents a moderate Froude number $F=0.5$, accompanying Fig. 3 with the dispersion relation. The four different radiated wave amplitudes are given as functions of their wave numbers. We have chosen the small shear rates $S^* = \pm 0.25$, including also the comparable case from Tyvand and Torheim [14] where vorticity is absent ($S^*=0$). We note the frequency of resonance where the third and fourth wave merge, and the associated wave amplitudes diverge.

Fig. 6

The dimensionless far-field elevation amplitude $|\zeta _{0}^*|$ of the radiated waves, as function of the dimensionless wave number $|k^*|$, for three different shear rates. A moderate value $F=0.5$ is chosen for the Froude number. Dotted curves represent $S^*=0$ (uniform flow). Solid curves represent $S^*=0.25$. Dashed curves represent $S^*=- 0.25$. The monotonously decreasing curves represent 10 $|\zeta _{1}^*(k_{1})|$ for the first (the longer downstream) wave. The other curves go to infinity at the critical wave number $k_{\textrm{c}}^*$. The left-hand branches of these discontinuous curves represent $|\zeta _{3}^*(k_{3})|$ for $0<|k^*_{3}|<|k^*_{\textrm{c}}|$. Their right-hand branches represent $|\zeta _{2}^*(k_{2})|$ and $|\zeta _{4}^*(k_{4})|$ for $|k^*|>|k^*_{\textrm{c}}|$

Figure 7 represents a the Froude number $F=0.25$ with the shear rates zero and $S^* = \pm 0.5$, where the corresponding dispersion relation has been displayed in Fig. 2 above. A positive shear rate will not have a monotonous influence on the radiation amplitude, reducing the amplitude for small frequencies but increase the amplitude for greater frequencies close to resonance.

Fig. 7

The dimensionless far-field elevation amplitude $|\zeta _{0}^*|$ of the radiated waves, as function of the dimensionless wave number $|k^*|$, for three different shear rates. The value $F=0.25$ is chosen for the Froude number. Dotted curves represent $S^*=0$ (uniform flow). Solid curves represent $S^*=0.5$. Dashed curves represent $S^*=- 0.5$. The monotonously decreasing curves represent 10 $|\zeta _{1}^*(k_{1})|$ for the first (the longer downstream) wave. The other curves go to infinity at the critical wave number $k_{\textrm{c}}^*$. The left-hand branches of these discontinuous curves represent $|\zeta _{3}^*(k_{3})|$ for $0<|k^*_{3}|<|k^*_{\textrm{c}}|$. Their right-hand branches represent $|\zeta _{2}^*(k_{2})|$ and $|\zeta _{4}^*(k_{4})|$ for $|k^*|>|k^*_{\textrm{c}}|$

In Figs. 7 and 8 we study smaller Froude numbers, where the behavior is more complicated, even though the wave radiation is less sensitive with respect to vorticity in the basic flow. Figure 8 enhances these tendencies of non-monotonous influence of shear on the radiation amplitude for the third wave, even though the Froude number $F=0.2$ reduces by only 20% the previously chosen value ($F=0.25$) in Fig. 7. A qualitative novelty in Fig. 8 is that the radiation amplitude for the third wave is quite large for small frequencies, whereby a local minimum emerges for the radiation amplitude as the source frequency is increased towards resonance. This is a qualitative novelty compared with Fig. 7, with only a small change in the Froude number. We omit plotting the dispersion relation corresponding to Fig. 8, and we choose not to pursue further these complications of smaller Froude numbers, sticking with results that maintain a certain relationship to the simpler physical problem with uniform basic flow [14].

Fig. 8

The dimensionless far-field elevation amplitude $|\zeta _{0}^*|$ of the radiated waves, as function of the dimensionless wave number $|k^*|$, for three different shear rates. The relatively small value $F=0.2$ is chosen for the Froude number. Dotted curves represent $S^*=0$ (uniform flow). Solid curves represent $S^*=1$. Dashed curves represent $S^*=- 1$. The continuous curves represent $|\zeta _{1}^*(k_{1})|$ for the first (long downstream) wave. The other curves go to infinity at the critical wave number $k_{\textrm{c}}^*$. The left-hand branches of these discontinuous curves represent $|\zeta _{3}^*(k_{3})|$ for $0<|k^*_{3}|<|k^*_{\textrm{c}}|$. Their right-hand branches represent $|\zeta _{2}^*(k_{2})|$ and $|\zeta _{4}^*(k_{4})|$ for $|k^*|>|k^*_{\textrm{c}}|$

4.4 On the Low-Frequency Limit

The low-frequency limit $\omega ^* \rightarrow 0$ includes the expected long-wave limits for the first wave and the third wave

$$\begin{aligned} \omega ^* \rightarrow 0\quad \text{ as }\ k_1^* \rightarrow 0^+\ \text{ and }\ k_3^* \rightarrow 0^-, \end{aligned}$$

(43)

which will be applied to expand the implicit dispersion relation (26). This means that the low-frequency limit for the first and third wave has first-order Taylor expansions for these wave numbers in terms of the frequency, without a constant zeroth-order term. Such leading-order Taylor expansions with a linear relationship between the frequency and a wavenumber will exist when $2 F \ne S^*$ and $F^2 \ne 1 + F S^*$. They imply the following low-frequency approximations valid for a long first wave and a long third wave

$$\begin{aligned} k_1^* = \omega ^* \left| \frac{S^* - 2 F}{1 + F S^* - F^2} \right| ,\quad k_3^* = - \omega ^* \left| \frac{S^* - 2 F}{1 + F S^* - F^2} \right| . \end{aligned}$$

(44)

These formulas are expected to be valid near the origin $(k^*, \omega ^*) = (0,0)$ for the diagrams $k^*(\omega ^*)$.

The second and fourth wave will have a different type of zero-frequency limit $\omega \rightarrow 0$: It is a limit where the wavenumbers $k_2$ and $k_4$ obey a common finite-wavenumber limit

$$\begin{aligned} \omega ^* \rightarrow 0\quad \text{ as }\ k_2^* \rightarrow k_0^*\ \text{ and }\ k_4^* \rightarrow - k_0^*, \end{aligned}$$

(45)

where only the sign is different, due to the opposite directions of the respective phase velocities. By taking the limit $\omega ^* \rightarrow 0$ in the dispersion relation (26) the wavenumber $k_0$ for these zero-frequency waves are found to be given by the transcendental equation

$$\begin{aligned} k_0^* \coth k_0^* = \frac{1 + F S^*}{F^2}, \end{aligned}$$

(46)

or, in terms of the shear rate

$$\begin{aligned} S^* = F k_0^* \coth k_0^* - \frac{1}{F}. \end{aligned}$$

(47)

We recall that $k_2^* = \vert k_0^*\vert$ in this limit, while $k_4^* = - \vert k_0^*\vert$. The two equivalent formulas (46) and (47) need no assumptions concerning the sign or magnitude of the wave number $k_0$, and can be compared with Figs. 2 and 3.

The exact zero-frequency case represents a steady source, which is a different physical process beyond the reach of the present mathematical model. It must be treated as an initial value problem. In the asymptotic low-frequency limit, the second and fourth wave approach zero phase velocity, but they have finite (downstream) group velocity, and they will also have a finite amplitude. The far-field amplitude for this asymptotic low-frequency limit can be expressed as

$$\begin{aligned} \vert \zeta _0^* \vert = \left| \frac{ k_j^* F }{(S^* F + 1) \sinh k_j^* - 2 F^2 k_j^* \cosh k_j^* + (k_j^* F)^2~ \text{ csch }~ k_j^*}\right| ,\quad (j = 2, 4), \end{aligned}$$

(48)

obtained by letting $\omega ^* \rightarrow 0$ in the general formula (42). Inserting $S^* F + 1 = F^2 k_j^* \coth k_j^*$, implied by Eq. (47), gives

$$\begin{aligned} \vert \zeta _0^* \vert = \left| \frac{ F^{-1} }{ (\sinh k_j^* - 2) \cosh k_j^* + k_j^*~ \text{ csch }~ k_j^*}\right| ,\quad (j = 2, 4). \end{aligned}$$

(49)

This is the common low-frequency limit formula for the radiated amplitude of the second and fourth wave, with the important distinction that $k_2^* = \vert k_0^*\vert$ while $k_4^* = - \vert k_0^*\vert$. The positive wavenumber $k_0$ is known as an implicit function of F and $S^*$ by Eq. (46). We note that $\vert \zeta _0^*\vert$ changes its value under the transformation $k^* \rightarrow -k^*$. Therefore the asymptotic low-frequency elevation for the second wave is not equal to that for the fourth wave.

Asymptotic low-frequency relationships for the group velocity $c_g^*$ of the second and fourth wave follow from Eq. (30), after determining $k_2^* = - k_4^* = \vert k_0^*\vert$, according to Eq. (47).

5 Summarizing Discussion

We have performed an analytical study of surface waves generated by oscillatory bottom vibrations in an open-channel flow with uniform vorticity. A concentrated (singular) oscillatory source at the bottom may serve to construct the Green function for water waves radiated from monochromatic bottom oscillations. The exact far-field wave amplitudes have been calculated, according to linear theory with the radiation condition of outgoing group velocity at infinity.

The present work is part two of an investigation of radiation of water waves from bottom oscillations with a shear flow. In this paper we take a nonzero surface flow into account. The radiation problem without a surface flow has been solved by Tyvand and Sveen [13]. The previous investigation with zero surface flow was simpler in several ways: All Doppler effects were absent. There was no resonance, and there were two distinct radiated waves: The first (longer) wave with phase velocity and group velocity in the downstream direction. The second (shorter) wave with both phase and group velocity in the upstream direction. The dispersion relation without a surface flow was qualitatively straightforward, even though it was implicit and must be calculated numerically. The asymmetry between the wavelengths and amplitudes in the upstream and downstream directions increases with the shear rate. The amplitude as a function of wave number had an inflection point at zero wave number, representing a common long-wave limit for the upstream and downstream waves. Our previous paper [13] confirmed the efficiency of a shear flow in strongly impeding the energy flux in the upstream direction, which was suggested by Brevik [2] as a blocking mechanism for water waves. Tyvand and Sveen [13] found that these upstream waves are never completely blocked when the surface flow is zero, as there is always nonzero subsurface energy flux in the upstream direction.

The present model includes a nonzero surface velocity, giving an implicit dispersion relation which has a complicated form. We have illustrated the dispersion relation for three chosen values of the Froude number, for the present model with finite depth. Tyvand and Lepperød [12] has given a more exhaustive presentation of the dispersion relation for this shear flow, with the simplifying assumption of an infinite depth.

The general radiation problem is very complicated because of the complexities in the implicit dispersion relation which depends on three physical parameters: the source frequency, the Froude number of the surface flow and the vorticity. The presence of a surface flow makes it possible to have resonance with zero group velocity, which is a qualitatively novelty in comparison with zero surface flow [13].

Our previous work treated the interesting limit of zero frequency, and linked it to the formation of bores. The zero-frequency limit is more complicated with a nonzero surface flow. The first and third wave will usually have zero wavenumber in the zero-frequency limit, but we identified certain exceptional combinations of Froude number and shear rate where this may not be the case. As a contrast, the zero-frequency limit gives finite wavenumbers for the second and fourth wave. While each of these waves have zero phase velocity, the group velocity will be finite, in the downstream direction. As pointed out by Brevik and Sollie [3], the concept of energy flux is more complicated in the presence of a surface flow, and is omitted from the present calculations.