Abstract
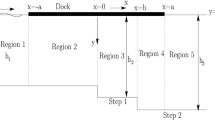
The three-dimensional problem involving diffraction of water wave by a finite floating rigid dock over an arbitrary bottom is studied for two cases (1) in the absence of wall (2) in the presence of wall. The problem is handled for its solution with the aid of step method. Here both asymmetric and symmetric arbitrary bottom profile is approximated using successive steps. Step approximation helps to apply the matched eigenfunction expansion method, in result, system of algebraic equations are obtained which are solved to determine the hydrodynamic quantities, namely, force experienced by rigid floating dock as well as rigid seawall, free surface elevation, transmission and reflection coefficients associated with transmission and reflected waves respectively. The effects of various structural and system parameters are examined on these hydrodynamics quantities. The appropriate values of length and thickness of dock, water depth and angle of incidence provide the salient information to marine and coastal engineers to design the offshore structures and creation of parabolic trench on the bottom. The present results are compared with known results in special case of bottom topography. The energy balance relation is derived and checked.
Similar content being viewed by others
References
Linton C. M. The finite dock problem [J]. Zeitschrift fr angewandte Mathematik und Physik ZAMP, 2001, 52(4): 640–656.
Chakrabarti A., Mandal B. N., Gayen R. The Dock problem revisited [J]. International Journal of Mathematics and Mathematical Sciences, 2005, 21: 3459–3470.
Cho I. H., Kim M. H. Interactions of a horizontal flexible membrane with oblique incident waves [J]. Journal of Fluid Mechanics, 1998, 367: 139–161.
Martha S. C., Bora S. N. Reflection and transmission coefficients for water wave scattering by a sea-bed with small undulation [J]. Journal of Applied Mathematics and Mechanics, 2007, 87(4): 314–321.
Xie J., Liu H. W. An exact analytic solution to the modified mild-slope equation for waves propagating over a trench with various shapes [J]. Ocean Engineering, 2012, 50: 72–82.
Lin P., Liu H. W. Analytical study of linear-wave reflection by a two-dimensional obstacle of general trapezoidal shape [J]. Journal of Engineering Mechanics, 2005, 131: 822–830.
Xie J. J., Liu H. W., Lin P. Analytical solution for long-wave reflection by a rectangular obstacle with two scour trenches [J]. Journal of Engineering Mechanics, 2011, 137(12): 919–930.
Wang, C. D., Meylan M. H. The linear wave response of a floating thin plate on water of variable depth [J]. Applied Ocean Research, 2002, 24: 163–174.
Xu F., Lu D. Q. An optimization of eigenfunction expansion method for the interaction of water waves with an elastic plate [J]. Journal of Hydrodynamics, 2009, 21(4): 526–530.
Karmakar D., Sahoo T. Gravity wave interaction with floating membrane due to abrupt change in water depth [J]. Ocean Engineering, 2008, 35(7): 598–615.
Dhillon H., Banerjea S., Mandal B. N. Water wave scattering by a finite dock over a step-type bottom topography [J]. Ocean Engineering, 2016, 113: 1–10.
Guo Y., Liu Y., Meng X. Oblique wave scattering by a semi-infinite elastic plate with finite draft floating on a step topography [J]. Acta Oceanologica Sinica, 2016, 35: 113–121.
Das S., Bora S. N. Reflection of oblique ocean water waves by a vertical porous structure placed on a multi-step impermeable bottom [J]. Applied Ocean Research, 2014, 47: 373–385.
Meng Q. R., Lu D. Q. Scattering of gravity waves by a porous rectangular barrier on a seabed [J]. Journal of Hydrodynamics, 2016, 28(3): 519–522.
Zhao W., Taylor P. H., Wolgamot H. A. et al. Amplification of random wave run-up on the front face of a box driven by tertiary wave interaction [J]. Journal of Fluid Mechanics, 2019, 869: 706–725.
Liu Y., Li Y., Teng B. Wave interaction with a new type perforated breakwater [J]. Acta Mechanica Sinica, 2007, 23(4): 351–358.
Liu Y., Li Y., Teng B. Interaction between obliquely incident waves and an infinite array of multi-chamber perforated caissons [J]. Journal of Engineering Mathematics, 2012, 74: 1–18.
Bhattacharjee J., Soares C. G. Wave interaction with a floating rectangular box near a vertical wall with step type bottom topography [J]. Journal of Hydrodynamics, 2010, 22: 91–96.
Behera H., Kaligatla R. B., Sahoo T. Wave trapping by porous barrier in the presence of step type bottom [J]. Wave Motion, 2015, 57: 219–230.
Koley S., Sahoo T. Oblique wave trapping by vertical permeable membrane barriers located near a wall [J]. Journal of Marine Science and Application, 2017, 16(4): 490–501.
Jung T. H., Suh K. D., Lee S. O. et al. Transformation of long waves propagating over trench [J]. Journal of Korean Society of Coastal and Ocean Engineers, 2007, 19: 228–236.
Roy R., Chakraborty R., Mandal B. N. Propagation of water waves over an asymmetrical rectangular trench [J]. The Quarterly Journal of Mechanics and Applied Mathematics, 2016, 70(1): 49–64.
Acknowledgment
The authors thank the reviewers and associate editor of Journal of Hydrodynamics for their comments and suggestions to improve the article in the present form. A. Kaur thanks DST, India for support through inspire fellowship.
Author information
Authors and Affiliations
Corresponding author
Additional information
Biography: Amandeep Kaur, Ph. D. Candidate
Rights and permissions
About this article
Cite this article
Kaur, A., Martha, S.C. Reduction of wave impact on seashore as well as seawall by floating structure and bottom topography. J Hydrodyn 32, 1191–1206 (2020). https://doi.org/10.1007/s42241-019-0076-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42241-019-0076-3