Abstract
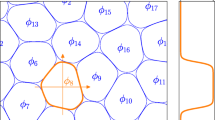
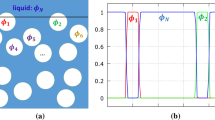
The single-film bubble has a special geometry with a certain amount of gas shrouded by a thin layer of liquid film under the surface tension force both on the inside and outside surfaces of the bubble. Based on the mesh-less moving particle semi-implicit (MPS) method, a single-film double-gas-liquid-interface surface tension (SDST) model is established for the single-film bubble, which characteristically has totally two gas-liquid interfaces on both sides of the film. Within this framework, the conventional surface free energy surface tension model is improved by using a higher order potential energy equation between particles, and the modification results in higher accuracy and better symmetry properties. The complex interface movement in the oscillation process of the single-film bubble is numerically captured, as well as typical flow phenomena and deformation characteristics of the liquid film. In addition, the basic behaviors of the coalescence and connection process between two and even three single-film bubbles are studied, and the cases with bubbles of different sizes are also included. Furthermore, the classic plateau structure in the foam system is reproduced and numerically proved to be in the steady state for multi-bubble connections.
Similar content being viewed by others
References
Chan D. Y. C., Klaseber E., Manica R. Film drainage and coalescence between deformable drops and bubbles [J]. Soft Matter, 2011, 7(6): 2235–2264,.
Yang L. T., Lv J. Q., Sun Y. H. et al. Theoretical analysis of leakage during the bubble size [J]. Machine Design and Manufacturing Engineering of China, 2010, 39 (3): 78–79 (in Chinese).
Zhang J. S., LV Q., Sun C. D. et al. High speed photography to motion of bubbles in water [J]. Photonics Journal, 2000, 29(10): 952–955(in Chinese).
Gu H. Y., Guo L.J., Zhang X. M. et al. Single bubbles in gas-liquid two-phase flow in a horizontal tube shape characteristics [J]. Journal of Engineering Physics, 2006, 27(3): 433–436(in Chinese).
Lu H., Shen Z., Ding J. et al. Numerical simulation of bubble and particles motions in a bubbling fluidized bed using direct simulation Monte-Carlo method [J]. Powder Technology, 2006, 169(3): 159–171.
Olmos E., Gentric C., Vial C. et al. Numerical simulation of multiphase flow in bubble column reactors Influence of bubble coalescence and break-up [J]. Chemical Engineering Science, 2001, 56(21-22): 6359–6365.
Liu H., Xie M. Z., Li K. et al. Liquid metal bath numerical simulation of bubble-liquid two-phase turbulent flow into metal melt [J]. Chinese Journal of Computational Mechanics, 2007, 24(5): 669–673(in Chinese).
Sungkorn R., Derksen J. J., Khinast J. G. Modeling of turbulent gas-liquid bubbly flows using stochastic Lagrangian model and lattice-Boltzmann scheme [J]. Chemical Engineering Science, 2011, 66(12): 2745–2757.
Chen L., Garimella S. V., Reizes J. A. et al. The development of a bubble rising in a viscous liquid [J]. Journal of Fluid Mechanics, 1999, 387: 61–96.
Zhang S. J., Wu C. J. Numerical simulation of the interaction between two three dimensional deformable bubbles [J]. Chinese Journal of Hydrodynamics, 2008, 23(6): 681–686(in Chinese).
Sussman M., Almgren A., Bell J. et al. An adaptive level set approach for incompressible two-phase flows [J]. Journal of Computational Physics, 1997, 148(1): 81–124.
Amaya-Bower L., Lee T. Single bubble rising dynamics for moderate Reynolds number using lattice Boltzmann method [J]. Computers and Fluids, 2010, 39(7): 1191–1207.
Yu Z., Yang H., Fan L. S. Numerical simulation of bubble interactions using an adaptive lattice Boltzmann method [J]. Chemical Engineering Science, 2011, 66(14): 3441–3451.
Koshizuka S. Oka Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid [J]. Nuclear Science and Engineering, 1996, 123(3): 421–434.
Sun Z. G., Xi G., Xiang L. F. Simulation on rising bubble in water with meshfree method [J]. Journal of Engineering thermo-physics, 2007, 28(5): 771–774.
Sun Z. G., Xi G., Chen X. A numerical study of stir mixing of liquids with particle method [J]. Chemical Engineering Science, 2009, 64(2): 341–350.
Sun Z., Xi G., Chen X. Mechanism study of deformation and mass transfer for binary droplet collisions with particle method [J]. Physics of Fluids, 2009, 21(3): 032106.
Chen X., Xi G., Sun Z. Improving stability of MPS method by a computational scheme based on conceptual particles [J]. Computer Methods in Applied Mechanics and Engineering, 2014, 278(7): 254–271.
Chen X., Sun Z. G., XI G. Improvement of the surface free energy model and numerical study on the infiltration of droplets [J]. Journal of Xiʼan Jiao Tong University, 2012, 46(7): 115–121(in Chinese).
Zhang S., Morita K., Fukuda K. et al. A new algorithm for surface tension model in moving particle methods [J]. International Journal for Numerical Methods in Fluids, 2010, 55(3): 225–240.
Kondo M., Koshizuka S., Suzuki K. et al. Surface tension model using inter-particle force in particle method [C]. ASME/JSME 2007 5th Joint Fluids Engineering Conference, San Diego, California, USA, 2007.
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Grant No. 51576154).
Rights and permissions
About this article
Cite this article
Sun, Zg., Ni, N., Sun, Yj. et al. Modeling of single film bubble and numerical study of the plateau structure in foam system. J Hydrodyn 30, 79–86 (2018). https://doi.org/10.1007/s42241-018-0008-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42241-018-0008-7