1 Introduction

Laterally loaded, thin-walled tubes have received considerable attention in the last 10 years [1, 2]. Most studies have focused on thin-walled, single-material structures [3]. Few studies on hybrid thin-walled tubes have been reported. In recent years, hybrid structures composed of multi-materials have been proposed to improve energy absorption (EA) and reduce the mass of thin-walled structures to enhance vehicle performance and fuel economy. Investigations showed that these components collapse by plastic bending, conforming to the plastic hinge model of lateral collapse of tubes. Given that strain energy is localized around plastic hinges, the dissipation of energy through lateral collapse is structurally inefficient [4].

Light materials, such as aluminium alloy, magnesium alloy, and composites, have received considerable attention because of their EA properties and reduced structural mass [5,6,7]. Investigations of magnesium alloys focused on the deformation behaviour and EA capability of circular tubes [8] and rectangular beams, as well as finite element simulations of responses to bending and axial compression [9, 10]. Some researchers have applied lightweight materials in hybrid structures to explore the potential and advantages of hybrid structures in crashworthiness. Hosseini-Tehrani et al. [11] studied the crashworthiness and lightweight properties of an S-shaped, steel–aluminium hybrid front rail. They reported that this significantly improved structural crashworthiness and reduced structural mass. The majority of research studies on optimizing crashworthiness of EA structures have focused on axially crushed devices [12, 13]. Research studies on the collapse behaviour and EA response of thin-walled hybrid tubes under lateral loading are less frequently reported [14, 15]. Designing lightweight hybrid tubes with optimal crashworthiness under lateral loading has received little attention.

First, this study performed experiments and simulations to investigate the EA characteristics and deformation mode of a double-hat-shaped tube composed of DC04. Based on these results, its deformation mode under quasi-static three-point bending load was identified as a combination of typical plastic hinge deformation and overall bending. For the same structural mass, different thicknesses of the top and bottom tubes resulted in different EA patterns. Thus, maximum EA could be obtained by optimizing tube thickness. Second, a double-hat-shaped tube composed of AZ31B, a magnesium alloy, was proposed and similarly investigated. Results indicated that it had a deformation pattern of plastic bending and partial fracture. Optimization results showed that the double-hat-shaped AZ31B tube had lower structural mass compared with the double-hat-shaped DC04 tube; however, to achieve the approximate EA of steel tube structures, the magnesium alloy wall thickness was too thick to manufacture and would fracture easily during bending, thus limiting its EA ability and rendering the bending process uncontrollable. Therefore, the double-hat-shaped AZ31B tube may be unsuitable for industrial applications. Based on the advantages and disadvantages of steel (stable EA but low specific energy absorption (SEA)) and magnesium alloy (higher SEA but easily fractured), two classes of hybrid tubes, namely the Hybrid-I tube (DC04 top hat and AZ31B bottom hat) and the Hybrid-II tube (AZ31B top hat and DC04 bottom hat), were then fabricated and studied experimentally and by simulation.

2 Materials, Experiments, and Methods

2.1 Materials

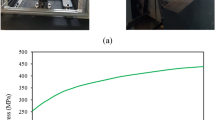
This study utilized AZ31B, a commercial and widely used lightweight magnesium alloy, and DC04, a traditional mild steel. To obtain tensile stress–strain data for AZ31B and DC04, quasi-static uniaxial tensile tests on dog-bone specimens were conducted at room temperature using a static universal material testing machine according to the testing standard GB/T 228.1-2010 [16]. The uniaxial compressive tests on AZ31B were conducted according to the testing standard GB/T 7314-2005 [17]. Figure 1a shows the measured true stress–strain curves of AZ31B in the rolling direction (RD), transverse direction (TD), and diagonal direction (DD) at room temperature. Figure 1b shows the quasi-static, true stress–strain curve of AZ31B under uniaxial tensile load in RD at room temperature [18].

Fig. 1
figure 1

Tensile–compressive true stress–strain curves for a AZ31B and b DC04

Full size image

As shown in Fig. 1a, AZ31B exhibited lower anisotropy of yield strength and a pronounced tension–compression asymmetry under both tension and compression. Moreover, AZ31B had lower yield strength and ultimate tensile strength than DC04. The mechanical properties of AZ31B under RD, TD, and DD are shown in Table 1 [19]. The total elongation of AZ31B was considerably lower than of DC04, indicating that AZ31B was more likely to rupture.

Table 1 Mechanical properties of DC04 and AZ31B under nominal strain rate of 0.001 s−1
Full size table

2.2 Specimen Geometry

Quasi-static three-point bending tests were performed on the double-hat-shaped DC04 and AZ31B tubes. In the bending tests, the double-hat-shaped tubes were composed of thin-walled structures. The tubes were 800 mm long with cross-sectional dimensions of 80 mm × 60 mm. Given that AZ31B has low ductility and ruptures too easily to produce mini-sized corners, rounded corners with 8 mm radii were adopted in the bending zone to prevent the initial damage. Tube wall thickness was selected as a design variable. The thicknesses of the top hat (t1) and bottom hat (t2) were considered as separate variables. Figure 2 shows the cross section of the thin-walled tubes.

Fig. 2
figure 2

Cross section of thin-walled, double-hat-shaped tube

Full size image

2.3 Three-Point Bending

2.3.1 Three-Point Bending Test

As shown in Fig. 3a, the quasi-static, three-point bending tests had one moving indenter and two fixed supporters. The specimen was placed horizontally between the indenter and supporters. The specimen would bend and even rupture as the indenter moved downward. To obtain a force–displacement curve of the bending process, the bending force and displacement of the moving indenter were recorded during bending collapse. The tests were conducted at a constant speed of 10 mm/min and were terminated when the indenter attained a constant displacement of 200 mm, which was greater than the collapse distance of the structure.

Fig. 3
figure 3

Three-point bending a test facility and b finite element model

Full size image

2.3.2 Three-Point Bending Simulation

LS_DYNA, an explicit finite element model (FEM) code, was employed to simulate bending collapse of the thin-walled, double-hat-shaped tubes under quasi-static, three-point bending. In this study, the material model MAT-24 in the LS-DYNA FEM package was specifically designed to simulate the isotropic and tension–compression symmetry of DC04.

Figure 3b shows the finite element (FE) models of the double-hat-shaped tubes. In the FE simulations, the tube was supported by two rigid supporters at the bottom and crushed by a rigid indenter at the top.

As shown in Fig. 1, AZ31B has obvious tension–compression asymmetry; however, because of its weak anisotropy in plan, the average tensile and compressive true stress–strain curves in three directions (RD, DD, and TD) were obtained and utilized instead. Based on the work of Zhou et al. [16, 17], simulation was conducted using the material model MAT-124 in LS-DYNA for a rectangular AZ31B tube under scheduled loading. The simulation results indicated that MAT-124 could yield good agreement with the experimental process after calibration of stress–strain curves and failure parameters.

MAT-124 is an isotropic, elastic–plastic material model wherein unique yield stress versus effective plastic strain curves can be defined for compression and tension. In this model, stress–strain behaviour followed a different curve in compression compared with that in tension. Tension was determined by the sign of the mean stress, where a positive mean stress (i.e. a negative pressure) indicated tension.

This study utilized three types of contact algorithms in LS-DYNA. *CONTACT_AUTOMATIC_SURFACE_TO_SURFACE defined contact between the rigid indenter, supporters, and DC04. Given that the AZ31B tube appeared to rupture during the bending process, *CONTACT_ERODING_SURFACE_TO_SURFACE defined contact between the rigid indenter, supporters, and AZ31B. To avoid self-penetration, *CONTACT_SINGLE_SURFACE was adopted to define self-contact of the samples. A bolt connection was adopted because the connection between top and bottom hats was not the focus of this study.

2.3.3 Assessment Criteria of Crashworthiness

Crashworthiness indicators were defined to evaluate the EA performance of the tested structures. Total EA and SEA are two commonly used crashworthiness indicators. EA is defined as follows:

$$ {\text{EA}} = \int\limits_{0}^{\delta } F {\text{d}}s , $$
(1)

where F is the bending force, ds is the bending displacement of the indenter under current bending force F, and δ is the total displacement of the indenter. SAE is defined as follows:

$$ {\text{SEA}} = \frac{\text{EA}}{{m_{1} + m_{2} }} , $$
(2)

where m1 and m2 are the masses of the top and bottom hats, respectively.

2.4 Optimization Method

Design-of-experiment (DOE) methods have recently been applied to construct surrogate models, such as the polynomial response surface method and radial basis function [20], to relate crushing and EA responses to design variables for analysis and optimization. The accuracy of the developed surrogate model can be verified by several techniques. The relative error (RE) between the observed response at sampling points (\( \hat{y} \)) and the original response (y) is given by:

$$ {\text{RE}} = \frac{{\hat{y} - y}}{y} . $$
(3)

Other important properties in evaluating the model’s accuracy are the correlation coefficient R2, adjusted \( R_{\text{adj}}^{2} \), and root-mean-square error (RMSE). According to the classical response surface theory, the larger the R2 and \( R_{\text{adj}}^{2} \) values and the smaller the RMSE and RE values, the better is the model fit. After selecting the appropriate surrogate model, we employed the NSGA-II algorithm in multi-objective design optimization.

3 Analysis of Different Types of Tubes

3.1 Double-Hat-Shaped Steel Tube

3.1.1 Experiment and Finite Element Simulation

The double-hat-shaped DC04 tube was utilized in experiments and FE simulations. The experiments aimed to acquire preliminary data on its EA characteristics and deformation behaviour.

Figure 4a shows that the DC04 tube exhibited a typical deformation mode of bending collapse. An inward fold at the top hat and two outward folds at the adjacent side walls formed a sectional crushing zone or plastic hinges. The localized sectional crushing zone subsequently reduced cross-sectional area, which was associated with decreased bending resistance after local sectional collapse occurred. As expected, no obvious ruptures were observed in the DC04 tube because of its superior ductility.

Fig. 4
figure 4

Deformation mode of DC04 tube under three-point bending. a Experimental and b simulation results

Full size image

Based on the deformation behaviour identified above, the force–displacement curve for the DC04 tube (Fig. 5) showed three characteristic phases: a linear elastic phase, a rapid plasticization phase up to peak crushing force, and a slow load drop phase attributed to localized buckling progression.

Fig. 5
figure 5

Force–displacement curves of DC04 tube in three-point bending

Full size image

Figures 4 and 5 also show a comparison of the force–displacement curves and deformation modes of the double-hat-shaped DC04 tube under experimental and simulated conditions. The deformation pattern of the double-hat-shaped DC04 tube under quasi-static three-point bending comprised plastic hinge deformation and overall bending. The consistency between the two force–displacement curves showed that the simulation was accurate and acceptable.

3.1.2 Influence of Hat Thickness on Energy Absorption

The influence of hat thickness on total EA was investigated by simulation. To reduce the impact of unrelated variables, the masses of all tubes were held constant, i.e. the total thickness of the tube was unchanged during the optimization process.

There was only one independent variable in the double-hat-shaped DC04 tube model, as shown in Eq. (4):

$$ \left\{ \begin{aligned} &t_{1} + t_{2} = 4\,{\text{mm}} \hfill \\ &0.4\,{\text{mm}} \le t_{1} \le 3.6\,{\text{mm}} \hfill \\ &0.4\,{\text{mm}} \le t_{2} \le 3.6\,{\text{mm}} \hfill \\ \end{aligned} \right. $$
(4)

Incremental thickness was set as 0.1 mm for manufacturing convenience. The total sample comprised 33 groups. Figure 6 shows the results obtained with LS-DYNA for the 33 samples.

Fig. 6
figure 6

Influence of thickness on energy absorption of DC04 tube

Full size image

Figure 6 shows that the appropriate combination of top- and bottom-hat thickness optimized EA. The maximum EA was adopted as a reference in the subsequent experiments analysing the EA characteristics of the double-hat-shaped AZ31B tube. Maximum energy was obtained when top- and bottom-hat thicknesses were set as 3.2 mm and 0.8 mm, respectively. This value was 2.322 kJ when the total mass was 4.587 kg.

3.2 Double-Hat-Shaped Magnesium Alloy Tube

3.2.1 Experiment and Finite Element Simulation

The tension–compression asymmetry and low ductility of magnesium alloy impeded simulation analysis. Therefore, this study first performed a three-point bending experiment on the double-hat-shaped AZ31B tube to ensure that the FE model was accurate. The same geometric parameters as for the double-hat-shaped DC04 tube were utilized.

The experimental and simulated force–displacement curves were obtained, and the simulation was validated. First, the linear stage of the simulated force–displacement curve corresponded with the experimental curve after slightly adjusting the stress–strain curve. Second, the effective plastic strain was set as the failure threshold value. An element was deleted from the calculation when its effective plastic strain reached the failure threshold value. Thus, cracks appeared and propagated in the simulation. Finally, the simulation results corresponded with the experimental results after calibration of the stress–strain curve and failure parameters. Figure 7a shows the final deformation of the double-hat-shaped AZ31B tube in three-point bending. Figure 7b shows the force–displacement curves. The consistency between the two force–displacement curves and final deformation modes validated the numerical simulation.

Fig. 7
figure 7

a Experimental and b simulated deformation mode of AZ31B tube

Full size image

The deformation pattern of the double-hat-shaped AZ31B tube comprised plastic bending deformation and partial cracks. The cracks mainly occurred on the sides of the top hat in contact with the rigid indenter. There were also a few cracks in the flange of the bottom hat.

Figure 8 shows a comparison of the experimental and simulated force–displacement curves of AZ31B tubes. The curves have three phases: a linear elastic phase, a slow plasticization phase up to peak crushing force, and a slow load drop resulting from fractures and localized buckling progression. There was a noticeable and sudden load drop near peak force because the AZ31B tube wall abruptly fractured at the compression wall. The curve was sustained because the bottom hat continued to bear load even after the top hat failed. The slow load drop occurred because of the combined effects of slow crack propagation and further plasticization. Comparing Fig. 5 with Fig. 8 revealed that, during bending, the force rapidly declined after peaking because the double-hat-shaped AZ31B tube ruptured during bending, thus weakening resistance to deformation. Rupturing also greatly weakened the EA capacity of the structure.

Fig. 8
figure 8

Force–displacement curves for double-hat-shaped AZ31B tube

Full size image

3.2.2 Crashworthiness Optimization of Double-Hat-Shaped Magnesium Alloy Tube

Changing top and bottom hat thickness minimized the total structural mass and guaranteed EA during bending. First, a series of discrete sample data was generated using the Latin hypercube design method [21]. Corresponding results were obtained by FE simulation. Second, surrogate models of the results were obtained. The most accurate surrogate model was determined by evaluating its fitness to facilitate optimization. Last, the optimized parameters were verified in a FE-simulated environment. In this experiment, the referenced EA was set as 2.322 kJ. Optimization aimed to minimize total mass. Given that total mass is equivalent to total thickness, the optimization problem can be written as (Table 2):

$$ \left\{ \begin{aligned} &{\text{Minimize}}\,f = (t_{1} + t_{2} ) \hfill \\ &s.t.A \ge 2.32KJ \hfill \\ &t_{1} \in (0,10];t_{2} \in (0,10] \hfill \\ \end{aligned} \right. $$
(5)
Table 2 Optimization results and finite element simulation verification of double-hat-shaped AZ31B tube
Full size table

The total mass of the double-hat-shaped AZ31B tube was approximately 55% of the double-hat-shaped DC04 tube, indicating excellent lightweight property; however, its optimal thickness was too thick to manufacture because of the low ductility of AZ31B.

It was very difficult to obtain thin-walled structures with corners when the AZ31B sheet was more than 6 mm thick because the corner areas ruptured easily. Therefore, the double-hat-shaped AZ31B tube may be difficult to use in practical applications despite its excellent lightweight properties.

3.3 Double-Hat-Shaped Hybrid Tube

3.3.1 Experiment and Finite Element Simulation

Based on the previous experiment, we knew that the double-hat-shaped AZ31B tube was unsuitable for use in lightweight designs because of its material properties. We also knew that DC04 has better ductility and that AZ31B has better lightweight properties. Therefore, a double-hat-shaped hybrid tube was proposed to combine the advantages of both materials.

Hybrid-I tube maintained its structural integrity by top-hat deformation. No cracks formed during the experiment. Plastic hinge and overall bending deformations were observed. A few cracks appeared in the middle of the flange in the bottom hat. Obvious cracks appeared in the top hat of the Hybrid-II tube and extended in a radial direction as the experiment progressed. No cracks were found in the bottom hat.

Figure 9 shows a comparison of the experimental and simulated force–displacement curves of the Hybrid-I and Hybrid-II tubes. The curves were in good agreement, proving the validity and reliability of the FE model. Thus, the FE model could be used for the next simulation.

Fig. 9
figure 9

Force–displacement curves for Hybrid-I and Hybrid-II tubes

Full size image

3.3.2 Crashworthiness Optimization of Double-Hat-Shaped Hybrid Tubes

Similar to double-hat-shaped AZ31B tubes, the two hybrid tubes were optimized by setting the reference EA as 2.322 kJ. Optimization aimed to minimize total mass. Table 3 shows the DOE factors and the levels of them. Table 4 shows that the optimization results were highly reliable and were validated by FE simulation.

Table 3 DOE factors and levels
Full size table
Table 4 Optimization results and finite element simulation validation of double-hat-shaped hybrid tube
Full size table

3.4 Discussion

Figure 10 shows that the double-hat-shaped AZ31B tube had the highest SEA; however, it was difficult to use in actual applications when the AZ31B sheet was more than 6 mm thick. Thus, the two hybrid structures may have more realistic opportunities for application. The optimum design parameters for Hybrid-I tube were t1 = 1.86 mm, t2 = 3.08 mm, and a total mass of 2.982 kg. The SEA of Hybrid-I tube was approximately 44.7% higher than that of the double-hat-shaped DC04 tube. The optimum design parameters for Hybrid-II tube were t1 = 3.97 mm, t2 = 2.65 mm, and a total mass of 4.066 kg. The SEA of Hybrid-II tube was approximately 12.7% higher than that of the double-hat-shaped DC04 tube. Therefore, Hybrid-I tube was more lightweight than Hybrid-II tube. When the maximum EA was 2.322 kJ and was set as the optimization constraint condition, Hybrid-I tube was 1.605 kg lighter than the double-hat-shaped DC04 tube and had a lightweight efficiency of approximately 34.9%.

Fig. 10
figure 10

Specific energy absorption performance of different tubes

Full size image

Figure 11 shows that the top hat mainly contributes to EA. Thus, the top hat should be appropriately designed to avoid serious failure during the bending process. Meanwhile, the bottom hat should be robust enough to support bending impact.

Fig. 11
figure 11

Energy absorption performance of different hats

Full size image

4 Conclusions

This study proposed double-hat-shaped tubes as EA components in automotive applications. The double-hat-shaped tubes were fabricated by combining AZ31B, a magnesium alloy, and DC04, a traditional mild steel. Tensile and compressive tests, three-point bending tests, and simulations were performed on the double-hat-shaped tubes. The main conclusions of this study are as follows:

  1. 1.

    In the three-point bending process, the top hat absorbed most of the impact energy and the bottom hat provided enough support to avoid fracture and failure. The bottom hat also absorbed some of the impact energy. Thus, selecting the appropriate material and thickness of the top and bottom hats can substantially improve the SEA of the double-hat-shaped tube.

  2. 2.

    AZ31B attained very high SEA; however, it fractured easily under bending or impact because ductility decreased at certain values of material thickness, thus preventing its practical application.

  3. 3.

    The potential advantage of the hybrid structure in SEA is associated with the combined advantages of its different component materials. The hybrid structure may contain more material capable of sustaining bending or impact.

  4. 4.

    Hybrid-I tube is more lightweight than Hybrid-II tube, indicating that, in designing double-hat-shaped tubes, highly ductile traditional materials, such as DC04, are more suitable for the compression (impact) side to ensure bending continuity and EA. A lightweight material, such as magnesium/aluminium alloy, may be more beneficial for the tension (support) side to ensure structural stability throughout the bending process.