The Bayesian Methodology of Sir Harold Jeffreys as a Practical Alternative to the P Value Hypothesis Test

Abstract

Despite an ongoing stream of lamentations, many empirical disciplines still treat the p value as the sole arbiter to separate the scientific wheat from the chaff. The continued reign of the p value is arguably due in part to a perceived lack of workable alternatives. In order to be workable, any alternative methodology must be (1) relevant: it has to address the practitioners’ research question, which—for better or for worse—most often concerns the test of a hypothesis, and less often concerns the estimation of a parameter; (2) available: it must have a concrete implementation for practitioners’ statistical workhorses such as the t test, regression, and ANOVA; and (3) easy to use: methods that demand practitioners switch to the theoreticians’ programming tools will face an uphill struggle for adoption. The above desiderata are fulfilled by Harold Jeffreys’s Bayes factor methodology as implemented in the open-source software JASP. We explain Jeffreys’s methodology and showcase its practical relevance with two examples.

Introduction

Frequently maligned and rarely praised, the practice of p value null hypothesis significance testing (NHST) nevertheless remains entrenched as the dominant method for drawing scientific conclusions from noisy data. The recent ASA policy statement on p values (Wasserstein and Lazar (2016); see also Wasserstein et al. (2019)) warns against common misinterpretations and abuses, but does not take a strong stance on what methodology should supplement or supplant the p value. Left without a concrete and workable alternative to test their hypotheses, practitioners arguably have little choice but to continue reporting and interpreting p values.

Promising alternatives to p value NHST do exist, however, and one of the most noteworthy is the Bayesian testing methodology advanced and promoted by the geophysicist Sir Harold Jeffreys (e.g., Etz and Wagenmakers 2017; Howie2002; Jeffreys 1961; Ly et al. 2016a, 2016b and Robert et al. 2009). We believe that Jeffreys’s methodology fulfils three important desiderata. First, the methodology is grounded on the assumption that a general law (e.g., the null hypothesis) has a positive point mass, allowing practitioners to quantify the degree to which it is supported or undermined by the data. Second, Jeffreys implemented his conceptual framework for several run-of-the-mill statistical scenarios; to facilitate practical application, he also derived adequate approximations for unwieldy analytic solutions. Third, Jeffreys’s tests and recent extensions are available in the open-source software program JASP (Jeffreys’s Amazing Statistics Program; http://jasp-stats.org). JASP has an attractive interface that allows the user to obtain a reproducible and comprehensive Bayesian analysis with only a few mouse clicks.

The outline of this paper follows that of the above desiderata: first, we summarise Jeffreys’s philosophy of scientific learning (developed together with his early collaborator Dorothy Wrinch), which makes the methodology relevant for practitioners; then, we describe how Jeffreys created concrete tests for common inferential tasks, making the methodology available; finally, we present two examples that demonstrate how JASP allows practitioners to obtain comprehensive Bayesian analyses with minimal effort, making the methodology easy to use.

First Desideratum: Relevance from Wrinch and Jeffreys’s Philosophy of Scientific Learning

At the start of the twentieth century, Wrinch and Jeffreys (1919, 1921, 1923) set out to develop a theory of scientific learning that allows one to quantify the degree to which observed data corroborate or undermine a general law (e.g., the null hypothesis ${\mathscr{H}}_{0}$; within the context of Newton’s equation, for instance, ${\mathscr{H}}_{0}$ may stipulate that the value of the gravitational constant equals $G = 6.674 \times 10^{-11} \tfrac {\text {m}^{3}}{\text {s}^{2} \text {kg}}$). Their theory demanded that (i) the general law is instantiated as a separate model ${\mathscr{M}}_{0}$ and (ii) the inference process is Bayesian. The first postulate is a manifestation of what may be called Jeffreys’s razor: ‘Variation is random until the contrary is shown; and new parameters in laws, when they are suggested, must be tested one at a time unless there is specific reason to the contrary.’ (Jeffreys 1961, p. 342). The idea is shared with the p value, but Wrinch and Jeffreys also demanded the specification of an alternative model ${\mathscr{M}}_{1}$ that relaxes the general law (e.g., Newton’s equation with G unrestricted, thus, an unknown parameter that has to be inferred from data).

The second postulate was the foundation for all of Jeffreys’s work in statistics: ‘The essence of the present theory is that no probability, direct, prior, or posterior, is simply a frequency.’ (Jeffreys 1961, p. 401). This postulate implies that all unknowns, such as whether ${\mathscr{M}}_{0}$ or ${\mathscr{M}}_{1}$ holds true, should be formalised as probabilities or ‘a reasonable degree of belief’ (Jeffreys 1961, p. 401). By setting prior model probabilities $P({\mathscr{M}}_{0}) \in (0,1)$ and $P({\mathscr{M}}_{1}) = 1 - P({\mathscr{M}}_{0})$, these can then be updated to posterior model probabilities $P({\mathscr{M}}_{j} \mid d)$, j = 0, 1 in light of the data d using Bayes’ rule. The ratio of these two quantities yields the crucial equation as follows:

$$ \underbrace{\frac{P(\mathcal{M}_{1} \mid d)}{P(\mathcal{M}_{0} \mid d)}}_{\text{Posterior model odds}} = \quad \underbrace{\frac{p(d \mid \mathcal{M}_{1})}{p(d \mid \mathcal{M}_{0})}}_{\text{BF}_{10} (d)} \underbrace{\frac{ P(\mathcal{M}_{1})}{P(\mathcal{M}_{0})}}_{\text{prior model odds}} $$

(1)

where $p(d \mid {\mathscr{M}}_{j}) = {\int \limits } f(d \mid \theta _{j}) \pi _{j} (\theta _{j}) \mathrm {d} \theta _{j}$ is the marginal likelihood of ${\mathscr{M}}_{j}$ with respect to the prior density $\pi _{j} (\theta _{j}) = \pi (\theta _{j} \mid {\mathscr{M}}_{j})$ on the free parameters within ${\mathscr{M}}_{j}$.

The Bayes Factor

The updating term BF₁₀(d) is known as the Bayes factor and quantifies the change from prior to posterior model odds brought about by the observations d. The Bayes factor has an intuitive interpretation: BF₁₀(d) = 7 indicates that the data are 7 times more likely under ${\mathscr{M}}_{1}$ than under ${\mathscr{M}}_{0}$, whereas BF₁₀(d) = 0.2 indicates that the observations are 5 times more likely under ${\mathscr{M}}_{0}$ than under ${\mathscr{M}}_{1}$. The Bayes factor can be used to quantify the evidence against, but also in support of ${\mathscr{M}}_{0}$, and it only depends on the observed data, unlike the p value which also depends on more extreme—but not observed—outcomes of a statistic.¹

The Bayes factor methodology can be generalised in several ways. Suppose that data d₁ are observed and two or more competing models are entertained. The posterior probability for model ${\mathscr{M}}_{j}$ can be obtained as follows:

$$ P(\mathcal{M}_{j} \mid d_{1}) = \frac{\text{BF}_{j0}(d_{1}) P(\mathcal{M}_{j}) }{ {\sum}_{j'} \text{BF}_{j'0}(d_{1}) P(\mathcal{M}_{j'})}, $$

(2)

where the sum in the denominator is over the set of all candidate models, and BF₀₀(d₁) = 1. If an all-or-none decision on the model space is required, we can use the $P({\mathscr{M}}_{j} \mid d_{1})$ to select a single model. Once a single model ${\mathscr{M}}_{j}$ is selected, the knowledge about its parameters is then given by the posterior density defined as follows:

$$ \pi_{j}(\theta_{j} \mid d_{1}, \mathcal{M}_{j}) = \frac{f(d_{1} \mid \theta_{j}) \pi (\theta_{j} \mid \mathcal{M}_{j})}{ \int f(d_{1} \mid \theta_{j}) \pi (\theta_{j} \mid \mathcal{M}_{j}) \mathrm{d} \theta_{j}} . $$

(3)

Alternatively, we may forego selection, retain the uncertainty across the model space and use Bayesian model averaging (BMA; e.g., Raftery et al. (1997)). To simplify matters, suppose that there are only two models and ${\mathscr{M}}_{0}$ has parameters θ₀, whereas ${\mathscr{M}}_{1}$ has parameters θ₁ = (δ, θ₀). We refer to θ₀ as the common parameters and refer to δ as the test-relevant parameter. The model-averaged posterior density of the common parameters θ₀ is as follows:

$$ \pi(\theta_{0} \mid d_{1}) = \sum\limits_{j'} \pi(\theta_{0} \mid d_{1}, \mathcal{M}_{j'}) P(\mathcal{M}_{j'} \mid d_{1}) . $$

(4)

The model-averaged posterior of the test-relevant parameter δ is a convex mixture of a point mass at zero and the posterior density within ${\mathscr{M}}_{1}$, that is,

$$ \pi (\delta \mid d_{1}) = \mathbf{1} \left \{ \delta = 0 \right \} P(\mathcal{M}_{0} \mid d_{1}) + \pi(\delta \mid d_{1}, \mathcal{M}_{1} ) P(\mathcal{M}_{1} \mid d_{1}). $$

(5)

Another natural generalisation of Jeffreys’s Bayes factor framework concerns sequential analysis and evidence updating. For instance, suppose that an original experiment yields data d₁, and a direct replication attempt yields data d₂. One may then compute a so-called replication Bayes factor (Ly et al. 2019) as follows:

$$ \text{BF}_{10}(d_{2} \mid d_{1}) = \frac{ \text{BF}_{10}(d_{1}, d_{2})}{\text{BF}_{10}(d_{1})}, $$

(6)

whenever d₁ and d₂ are exchangeable. Note that BF₁₀(d₂∣d₁) quantifies the additional evidence for ${\mathscr{M}}_{1}$ over ${\mathscr{M}}_{0}$ provided by the data d₂ of the replication attempt given d₁. The total Bayes factor BF₁₀(d₁, d₂) is practical for collaborative learning, whereas the replication Bayes factor quantifies the individual contribution of the replication attempt.

Bayes Factor Rationale

For a deeper appreciation of the fact that scientific learning (i.e., the conformation and disconfirmation of a general law) requires both of Wrinch and Jeffreys’s postulates, we illustrate their main argument with a recent example. Pisa et al. (2015) considered the hypothesis that Alzheimer’s disease has a microbial aetiology; specifically, the hypothesis states that all Alzheimer’s patients have fungal infections in their brains. To provide evidence for this ${\mathscr{H}}_{0}$, they investigated a sample of deceased patients. Let y denote the observed number of Alzheimer’s patients with fungal infections in their brains out of a total number n who were examined. Here, ${\mathscr{M}}_{0}$ implies that $Y \sim \text {Bin}(n, \vartheta )$ with the restriction ${\mathscr{H}}_{0}: \vartheta = 1$, whereas ${\mathscr{H}}_{1}: \vartheta \in (0, 1)$.

As ${\mathscr{M}}_{0}$ does not have any free parameters, only π₁(𝜗) needs to be specified in order to obtain a Bayes factor. Following Wrinch and Jeffreys, let π₁(𝜗) = 1 on (0,1). A direct computation shows that $\text {BF}_{01} (d) = (n+1) \mathbf {1} \left \{ y=n \right \}$, where $\mathbf {1} \left \{ y=n \right \}$ is one whenever y = n, and zero otherwise. For the data d₁ : y₁ = n₁ = 10 of Pisa et al. (2015), this yields BF₀₁(d₁) = 11, thus evidence in favour of their proposed null hypothesis.

Note that with $\text {BF}_{01}(d) = (n+1) \mathbf {1} \left \{ y=n \right \}$, the evidence for ${\mathscr{M}}_{0}$ continues to grow with n as long as only confirming cases are observed. Upon encountering a single disconfirming case, however, we have BF₀₁(d) = 0 and $P({\mathscr{M}}_{0} \mid d) = 0$, meaning that ${\mathscr{M}}_{0}$ is falsified or ‘irrevocably exploded’ (Polya 1954, p. 6), regardless of the number of previously observed successes.

Bayes Factors Versus Bayesian Estimation

According to Wrinch and Jeffreys, a separate ${\mathscr{M}}_{0}$ is necessary for falsification and sensible generalisations of ${\mathscr{H}}_{0}$. This meant a radical departure from the Bayesian estimation procedures that had been standard practice ever since the time of Laplace. In the Laplace approach, the problem is treated as one of Bayesian estimation, and the uniform prior π₁(𝜗) under ${\mathscr{M}}_{1}$ implies that the prior probability of ${\mathscr{H}}_{0}: \vartheta = 1$ is zero. For d : y = n = 1,000, π₁(𝜗∣d) would then have a median of $\tilde {\vartheta } = 0.999$ and an approximate central 95% credible interval of [0.996,1.000]. The introduction of a single failure, which ‘irrevocably explodes’ the null hypothesis, only leads to a small shift in the posterior distribution, resulting in a π₁(𝜗∣d) with median $\tilde {\vartheta } = 0.998$ and an approximate central 95% credible interval of [0.994,1.000].

Furthermore, without a separate ${\mathscr{M}}_{0}$, the predictions for new data d₂ given d₁ only involve the posterior predictive under ${\mathscr{M}}_{1}$, that is, $p (d_{2} \mid d_{1}, {\mathscr{M}}_{1}) = {\int \limits } f(d_{2} \mid \theta _{1}) \pi (\theta _{1} \mid d_{1}, {\mathscr{M}}_{1}) \mathrm {d} \theta _{1}$. For example, when d₁ : y₁ = n₁ = 10, then a new sample d₂ : y₂ = n₂ consistent with ${\mathscr{M}}_{0}$ is predicted to occur with chance $p(d_{2} \mid d_{1}, {\mathscr{M}}_{1}) = 11/(11+n_{2})$; when n₂ = 11, this chance is 50%; when $n_{2} \rightarrow \infty$, this chance goes to 0. In other words, in the Laplace estimation framework, the proposition that fungal infections are not a necessary and sufficient cause of Alzheimer’s disease is a foregone conclusion. Jeffreys (1980) felt such generalisations violated common sense.²

Generalisations based on the Wrinch and Jeffreys posterior model probabilities $P({\mathscr{M}}_{j} \mid d_{1})$ are very different from the ones that follow from the Laplace estimation approach. Suppose that Pisa et al. (2015) set $P({\mathscr{M}}_{0})=P({\mathscr{M}}_{1})=1/2$, then $P({\mathscr{M}}_{0} \mid d_{1} ) = \frac {n_{1}+1}{n_{1}+2} = \frac {11}{12} \approx 0.917$ and $P({\mathscr{M}}_{1} \mid d_{1}) \approx 0.083$. If ${\mathscr{M}}_{0}$ is selected—and the uncertainty of this selection, $P({\mathscr{M}}_{1} \mid d_{1}) = 0.083$, is ignored—then d₂ : y₂ = n₂ = 11 is predicted to occur with 100% chance, which is a quite confident and perhaps risky generalisation of d₁. On the other hand, the Bayesian model–averaged prediction is defined as follows:

$$ p(d_{2} | d_{1}) = \sum\limits_{j^{\prime}} p(d_{2} | d_{1}, \mathcal{M}_{j^{\prime}}) P(\mathcal{M}_{j^{\prime}} | d_{1}), $$

(7)

and for d₂ : y₂ = n₂ = 11 given d₁ : y₁ = n₁ = 10, this yields a chance of 95.7%.

Bayes Factors Versus the P value

The p value takes ${\mathscr{M}}_{0}$ seriously, but does not assign it a prior model probability; also, the computation of the p value does not involve the specification of ${\mathscr{M}}_{1}$. Consequently, p values do not allow probabilistic statements about ${\mathscr{M}}_{0}$. For the Alzheimer example with y = n, the p value equals 1 regardless of the number of confirmatory cases n, which illustrates that the p value cannot be used to quantify evidence in support of ${\mathscr{M}}_{0}$. It is also unclear how p values could be used to average predictions. The p value does, however, allow for falsification as the observation of a single failure yields p = 0 < α for any α > 0.

Bayes Factor Relevance

The philosophy of scientific learning as articulated by Wrinch and Jeffreys is relevant to empirical researchers in two main ways. First of all, the philosophy allows one to test hypotheses. In contrast, some statistical reformers have argued that empirical researchers should abandon testing altogether and focus instead on estimating the size of effects (e.g., Cumming (2014)). We believe the estimation-only approach cannot address the primary goal that many researchers have, which is—for better or for worse—to convince a sceptical audience that their effects are real. Before interpreting the size of effects, one needs to be convinced that the effects exist at all. The estimation-only approach violates Jeffreys’s razor, leads to questionable generalisations, and starts out by assuming the very thing that many researchers seek to establish: the presence of an effect (Haaf et al. 2019).

Wrinch and Jeffreys’s philosophy of scientific learning is also relevant because it allows practitioners to quantify evidence—the degree to which the data support or undermine the hypothesis of interest. The Bayesian formalism allows researchers to update their knowledge in a coherent fashion, which allows a straightforward extension to techniques such as BMA and sequential analysis.

Second Desideratum: Availability for Common Statistical Scenarios

In Chapter V of ‘Theory of Probability’ (first edition 1939, second edition 1948, third edition 1961), Jeffreys demonstrates how his philosophy of scientific learning can be implemented for common statistical scenarios. In all scenarios considered, Jeffreys was confronted with a nested model comparison ${\mathscr{M}}_{0} \subset {\mathscr{M}}_{1}$, and he set out to choose a pair of prior densities (π₀, π₁) from which to construct a Bayes factor, that is,

$$ \text{BF}_{10}(d) = \frac{ \int \int f(d | \theta_{0}, \delta) \pi_{1}(\theta_{0}, \delta) \mathrm{d} \theta_{0} \mathrm{d} \delta}{ \int f(d | \theta_{0}, \delta=0) \pi_{0}(\theta_{0}) \mathrm{d} \theta_{0}} . $$

(8)

The main challenge is that general ‘noninformative’ choices lead to Bayes factors with undesirable properties. Specifically, prior densities of arbitrary width yield Bayes factors that favour ${\mathscr{M}}_{0}$ irrespective of the observed data. Furthermore, the prior density on the test-relevant parameter must be proper, as improper priors contain suppressed normalisation constants and lead to Bayes factors of arbitrary value.

To overcome these problems for his one-sample t test (e.g., Jeffreys (1961); p. 268–274; Ly et al. 2016a, 2016b), Jeffreys used invariance principles and two desiderata to select π₀ and π₁. The desideratum of predictive matching states that the Bayes factor ought to be perfectly indifferent, i.e., BF₁₀(d) = 1, in case n is too small; the desideratum of information consistency implies falsification of ${\mathscr{M}}_{0}$, as it requires $\text {BF}_{10}(d) = \infty$ in case data of sufficient size are overwhelmingly informative against ${\mathscr{H}}_{0}$.

The same two desiderata that Jeffreys formulated for his one-sample t test were extended and used to construct Bayes factors for correlations (e.g., Ly et al. (2018b)), linear regression (e.g., Bayarri et al. (2012), Liang et al. (2008), and Zellner and Siow (1980)), ANOVA (e.g., Rouder et al. (2012)), and generalised linear models (e.g., Li and Clyde (2018))—scenarios that are highly relevant to contemporary empirical researchers.

In addition, recent results show that these (group invariant) Bayes factors are robust under optional stopping (Hendriksen et al. 2018; Grünwald et al. 2019). Hence, the data collection can be stopped when the result is sufficiently compelling or when the available resources have been depleted, without increasing the chance of a false discovery. Furthermore, it was shown that $\text {BF}_{j0}(d) = \mathcal {O}_{P}(n^{-1/2})$ for data generated under ${\mathscr{M}}_{0}$, and $\text {BF}_{j0}(d) = \mathcal {O}_{P}(e^{n D(\theta _{j}^{*} \| {\mathscr{M}}_{0})} )$ for data generated under ${\mathscr{M}}_{j}$ for j≠ 0, where $D(\theta _{j}^{*} \| {\mathscr{M}}_{0})$ is the Kullback–Leibler projection of the true $\theta _{j}^{*}$ parameter value onto the null model (e.g., Johnson and Rossell (2010)). Hence, if δ≠ 0, it will be detected relatively quickly.

Throughout his own work, Jeffreys devised ingenious approximations to facilitate the use of his Bayes factors in empirical research. But, despite the tests being relevant and readily available, empirical researchers for some years largely ignored Jeffreys’s Bayes factors. Their lack of popularity can be explained not only by Jeffreys’s unusual notation and compact writing style but also by the fact that during his lifetime Bayesian approaches were not yet mainstream.

Third Desideratum: Ease of Use Through JASP

In order to make Bayesian statistics more accessible to practitioners, we have developed JASP, an open-source software package with an intuitive graphical user interface. Built on R (R Development Core Team 2004), JASP allows practitioners to conduct comprehensive Bayesian analyses with minimal effort. JASP also offers frequentist methods, making it straightforward to check whether the two paradigms support the same conclusion.

One of JASP’s design principles is that the Bayesian analyses come with default prior specifications that yield reference-style outcomes. For example, the default settings for most tests in JASP define Bayes factors that adhere to Jeffreys’s method of learning, that is, they are predictively matched and information consistent. The following two examples demonstrate how JASP allows a straightforward application of Jeffreys’s philosophy of scientific learning in practical situations.³

Example 1: Bayesian Independent Samples t Tests

The t test is designed to address the fundamental question of whether two means differ. Below, we first outline the default Bayes factor t test (see also Gönen et al. (2005) and Rouder et al. (2009)) and then use it to reanalyse a seminal psychological experiment as well as a recent replication attempt.

Bayesian Background

For the comparison of two sample means, the k th sample, k = 1, 2, is assumed to be normally distributed as $\mathcal {N} (\mu _{k}, \sigma ^{2})$, where μ_k = μ_g + (− 1)^k− 1σδ/2 and where μ_g is interpreted as a grand mean and δ as the effect size. Hence, for ${\mathscr{M}}_{0}$, we have θ₀ = (μ_g, σ), whereas ${\mathscr{M}}_{1}$ has one more parameter; θ₁ = (δ, θ₀). In this case, Jeffreys’s invariance principle leads to the right Haar prior π₀(θ₀) ∝ σ^− 1 on the common parameters and π₁(δ, θ₀) = π₁(δ)π₀(θ₀). Predictive matching requires π₁(δ) to be symmetric around zero, whereas information consistency requires that π₁(δ) is without moments.

Following Jeffreys, π₁(δ) is assigned a zero-centred Cauchy prior, but with default width $\kappa =1/\sqrt {2}$ (Rouder et al. 2012). This default Bayes factor is recommended at the start of an investigation, as it is invariant (a) under permutation of the group membership label k and (b) under location-scale transformation of the units of measurements, for instance, from Celsius to Fahrenheit.

Default Bayesian Analysis of an Original Study

To demonstrate this default Bayes factor in practice, we first reanalyse a seminal study on the facial feedback hypothesis of emotion. Specifically, Strack et al. (1988) reported that people rate cartoons as more amusing when they have to hold a pen between their teeth (the ‘smile’ condition) than when they have to hold a pen with their lips (the ‘pout’ condition).

Unfortunately, the raw data from this study are no longer available. However, the Summary Stats module in JASP affords a comprehensive Bayesian reanalysis using only the test statistics and the sample sizes obtained from the original article (Ly et al. 2018a).⁴ According to Strack et al. (1988)’s working hypothesis, participants in the smile condition are expected to judge the cartoons to be more funny—not less funny—than participants in the pout condition. The directional nature of the alternative hypothesis is acknowledged by formalising it as ${\mathscr{H}}_{+}: \delta > 0$, which we pitted against ${\mathscr{H}}_{0}: \delta = 0$. Entering d₁ : t = 1.85, n₁ = n₂ = 32 into JASP immediately yields BF_+ 0(d₁) = 2.039, which represents weak evidence for Strack et al. (1988)’s working hypothesis. A single tick mark in JASP produces the left panel plot from Fig. 1. This plot shows the prior and posterior distributions for effect size under ${\mathscr{H}}_{+}$. The posterior is relatively wide, indicating that there remains considerable uncertainty about the size of the effect. In addition, the two grey dots at δ = 0 provide a visual representation of the Bayes factor as the ratio of the prior and posterior density under ${\mathscr{M}}_{+}$ evaluated at the restriction ${\mathscr{H}}_{0}: \delta = 0$ (Dickey 1971). The probability wheel on top confirms that the evidence for ${\mathscr{M}}_{+}$ is rather meagre. The area of the red surface equals $P({\mathscr{M}}_{+} \mid d_{1} )$ under the assumption that $P({\mathscr{M}}_{0})=P({\mathscr{M}}_{+})=1/2$.

Fig. 1

A Bayes factor reanalysis of Strack et al. (1988). Left panel: The data show anecdotal evidence in favour of the alternative hypothesis. Right panel: Robustness check for different specifications of the width of the Cauchy prior on δ. Figures from JASP

Another tick mark in JASP produces the right panel plot from Fig. 1. This plot shows the robustness of the Bayes factor to the width κ of the Cauchy prior on effect size. In this case, reasonable changes in κ lead to only modest changes in the resulting Bayes factor. The classification scheme on the right axis is based on Jeffreys (1961, Appendix B) and provides a rough guideline for interpreting the strength of evidence.

In sum, from a relatively comprehensive Bayesian reanalysis, we conclude that (a) the data from the original experiment provide weak evidence in favour of Strack et al. (1988)’s working hypothesis; (b) this inference is robust to reasonable changes in the width of the Cauchy prior on effect size; (c) there remains considerable uncertainty about the size of the effect, assuming that it is positive. The entire analysis is obtained from JASP by typing three numbers and ticking two boxes.

Informed Bayesian Analysis of a Replication Attempt

Wagenmakers et al. (2016) recently conducted a multi-lab direct replication of the original facial feedback study. We use data from the Wagenmakers’ lab and compare the results of a default analysis to an informed analysis based on expert knowledge and to an analysis that conditions on the original data.

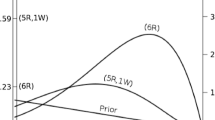
First, the same default analysis as described in the previous section yields BF_+ 0(d₂) = 0.356, thus, weak evidence in favour of ${\mathscr{M}}_{0}$. Second, Gronau et al. (2017) elicited an informed prior density from Suzanne Oosterwijk, an expert in the field. This elicitation effort resulted in a positive-only t-prior on δ with location 0.350, scale 0.102, and 3 degrees of freedom. The left panel of Fig. 2 shows that $\text {BF}_{+0}^{\text {info}}(d_{2}) = 0.597$, which is weak evidence in favour of ${\mathscr{M}}_{0}$. The right panel of Fig. 2 shows the evidential flow, that is, the progression of the Bayes factor as the experimental data accumulate.

Fig. 2

An informed Bayesian analysis of the Wagenmakers replication data reported in Wagenmakers et al. (2016). Left panel: The Bayes factor indicates anecdotal evidence in favour of the null hypothesis. Right panel: Sequential monitoring of the Bayes factor as experimental data accumulate. Figures from JASP

Third, the test may also be informed by using π₊(δ∣d₁) as a prior, which is equivalent to conditioning on the original data set, when d₁ and d₂ are exchangeable. As the total Bayes factor is BF_+ 0(d₁, d₂) = 1.400, this leads to BF_+ 0(d₂∣d₁) = 0.686, which is again weak evidence in favour of the null hypothesis.

We can also examine the maximum evidence—that is, the evidence obtained when a proponent of the effect were to cherry-pick a ‘prior’ after data inspection in order to achieve the highest possible Bayes factor (Edwards et al. 1963). This Bayes factor is obtained using an oracle prior on δ that assigns all prior mass to the maximum likelihood estimate, approximately $\hat {d} = 0.4625$, which leads to $\text {BF}_{+0}^{\max \limits }(d_{1}) = 5.26$. Although this cheating strategy leads to more evidence in favour of ${\mathscr{M}}_{1}$ given original data d₁, in light of new data d₂, it leads to a larger decrease, as $\text {BF}_{+0}^{\max \limits }(d_{1}, d_{2})=1.97$, and, therefore, $\text {BF}_{+0}^{\max \limits }(d_{2} \mid d_{1})=0.37$, which is more evidence for ${\mathscr{M}}_{0}$ than provided by the default replication Bayes factor BF_+ 0(d₂∣d₁) = 0.69.

The above results are summarised in Table 1. None of the analyses provide compelling evidence for the hypothesis that cartoons are judged to be more funny in the smile condition than in the pout condition. The analyses that involve only the replication attempt all show weak evidence in favour of the null hypothesis. The analyses can be executed in JASP with minimal effort.

Table 1 Bayes factors for the original study by Strack et al. (1988) and the replication attempt by Wagenmakers et al. (2016)

Example 2: Bayesian Linear Regression

Linear regression allows researchers to examine the association between a criterion variable and several possible predictors or covariates. Whereas the t test featured only two models, ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, linear regression features 2^p models, where p is the total number of mean-centred potential predictors. With a model space this large, it is unlikely that any single model will dominate; consequently, a Bayesian model averaging (BMA) approach is advisable.

Bayesian Background

Each regression model can be identified with an indicator vector γ ∈{0,1}^p, where γ_k = 1 implies that the k th predictor is included in the model, whereas γ_k = 0 implies that it is excluded. Note that $| \gamma | = {\sum }_{k=1}^{p} \gamma _{k}$ defines the number of predictors included in ${\mathscr{M}}_{\gamma }$. We then have the following:

$$ \mathcal{M}_{\gamma}: Y \sim \mathcal{N}(\alpha \vec{1} + X_{\gamma} \beta_{\gamma}, \sigma^{2} I ), $$

(9)

where Y is the criterion variable, $\vec {1}$ is a vector of ones, I is the n × n identity matrix, and α and σ² are the intercept and variance parameters that are present in all models. Importantly, X_γ and β_γ are the included columns of the design matrix and regression coefficients, respectively. The baseline model ${\mathscr{M}}_{0}$ is specified by γ of all zeroes, which all 2^p models can be compared to. For BF_γ0(d) to not depend on the units of measurements Y and X_γ, we set π₀(α, σ) ∝ σ^− 1, and the coefficients are reparametrised in terms of $\xi _{\gamma } = \left (\tfrac {1}{n} X_{\gamma }^{T} X_{\gamma }\right )^{1/2} \beta _{\gamma }/ \sigma$, which implies that the regression is effectively executed on the standardised X_γ. Predictive matching and information consistency follow from choosing a zero-centered multivariate Cauchy prior on ξ_γ within ${\mathscr{M}}_{\gamma }$ (Zellner and Siow 1980). To facilitate computation, the multivariate Cauchy prior can be rewritten as a mixture of normals (Liang et al. 2008), which amounts to $\beta _{\gamma } \sim \mathcal {N} \left (0, g \left (X_{\gamma }^{T} X_{\gamma }\right )^{-1} \sigma ^{2}\right )$ and $g \sim \text {InvGam}\left (\tfrac {1}{2}, \tfrac {n \kappa ^{2}}{2}\right )$.

With 2^p models, the importance of an individual predictor may be assessed by averaging over the model space. In JASP, default prior model probabilities are assigned with a beta-binomial distribution. In particular, with beta(1,1), this yields $P({\mathscr{M}}_{\gamma }) = \frac {1}{p+1} \binom {p}{|\gamma |}^{-1}$, which implies that the prior mass is first divided evenly over the classes of models with 0,1,…, p number of active predictors, and then, within each such class, the 1/(p + 1) mass is divided evenly over the total number of available models. This beta-binomial prior assignment acts as an automatic correction for multiplicity (Scott and Berger 2010).

The JASP implementation of this linear regression analysis uses the R package BAS (Clyde 2010), which has been designed for computational efficiency and offers a range of informative output summaries.

Bayesian Analysis of the US Crime Rate Data

We analyse a well-known data set concerning US crime rates (Ehrlich 1973). This data set contains aggregate information about the crime rates of 47 US states, as well as a variety of demographic variables such as labour force participation and income inequality. Without the indicator variable for a Southern state, there are 14 predictors in total, and hence 2¹⁴ = 16,384 models to consider. After identifying the criterion variable and the potential predictors, ticking the box ‘Posterior Summaries of Coefficients’ makes JASP return the information shown in Table 2. For each regression coefficient, averaged across all 16,384 models, the table provides the posterior mean, the posterior standard deviation, the prior and posterior model probabilities summed across the models that include the predictor (i.e., P(incl) and P(incl∣data), respectively), and a posterior central 95% credible interval.

Table 2 Posterior summaries of regression coefficients for the US crime rate data

A more detailed inspection is provided by ticking the option ‘Marginal posterior distributions’. For instance, for the predictor ‘police expenditure’, this results in Fig. 3, which shows a model-averaged posterior density for the associated regression coefficient. The vertical bar represents the point mass at zero; the posterior mass away from zero is obtained as a weighted mix of the posterior distributions for the models that include ‘police expenditure’ as a predictor. The mixing is apparent from the slightly irregular shape of the model-averaged posterior.

Fig. 3

Model-averaged posterior densities over police expenditure in 1960 (Po1)

Concluding Remarks

Why have theoretical statisticians been unable to move the needle on the dominance of the p value? What has prevented practitioners from adopting a more inclusive statistical approach? The answer, we believe, is that statistics has largely failed to offer practitioners a workable alternative to the p value. In this paper, we have argued that the testing methodology of Sir Harold Jeffreys—developed in the 1930s and recently implemented in the JASP program—constitutes such a workable alternative. With JASP, users can compute p values; but, with just a few mouse clicks, they can also conduct a relatively comprehensive Bayesian analysis. Users may adjust prior distributions, quantify and monitor evidence, conduct sensitivity analyses, engage in model averaging, and more.

We believe that Bayesian statistics deserves to be applied more often, especially in practical, run-of-the-mill research problems. A pragmatist may argue that –irrespective of one’s statistical convictions—it is prudent to report the results from multiple paradigms. When the results point in the same direction, this bolsters one’s confidence in the conclusions; when the results are in blatant contradiction, one’s confidence is tempered—either way, something useful has been learned.