1 Introduction

The peridynamic (PD) theory was first introduced by Silling in the year of 2000 [1]. It is basically the re-formulation of classical continuum mechanics (CCM) equations using integro-differential equations, in which derivatives only come into picture with time derivatives of displacements. Both theories assume that a domain, V, can be discretized into many infinitesimal volumes, i.e. material points and their interactions. In CCM, the material point at position x only interacts with its nearest neighbors whereas in PD theory it can interact with material points x’ which are not only limited to the nearest neighbors of x. The former local interactions are in the form of traction vectors, T as opposed to the nonlocal force densities, t and t’ in PD theory. In CCM, the traction vectors are expressed in the form of stress tensor, σij and its equation of motion can be expressed as

$$ \rho(\mathbf{x})\ddot{\mathbf{u}}(\mathbf{x},\mathit{t})=\boldsymbol{\sigma}_{ij,j}+\mathbf{b}(\mathbf{x},\mathit{t})\quad\text{with}\quad \mathrm{i} \& \mathrm{j} = 1,2,3 $$
(1)

where comma in the subscript of the stress tensor indicates the differentiation over a space and u and b are the displacement and body load vectors, respectively. Moreover, ρ and t denote the density of the material and time, respectively. On the other hand, peridynamic theory has the following form of equation of motion

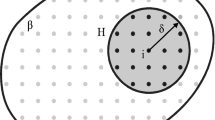
$$ \rho(\mathbf{x})\ddot{\mathbf{u}}(\mathbf{x},\mathit{t})={\int}_{H_{x}}\mathbf{(t(x^{\prime}-x, u^{\prime}-u)-t^{\prime}(u-u^{\prime}))}d\mathrm{H_{x}}+\mathbf{b}(\mathbf{x},\mathit{t}) $$
(2)

where integration region Hx includes all interactions between the main material point x and its family members x’. The range of interactions, generally called as bonds, is limited with the horizon, δ around the material point x. The force density, t arises from the relative displacements of all material points, x’ with respect to material point x with in the horizon of material point x. The force density, t’ is exerted upon the material point x in the opposite direction in ordinary state-based peridynamic formulation. In the original form of PD theory, which is named as bond-based PD theory, it is assumed that the force densities have the same magnitude and this assumption causes a restriction on material constants which lead to one material constant instead of two constants for isotropic materials. PD theory has attracted attention of many researchers all over the world. The reason of this is mainly the capability of PD theory for modeling discontinuities over a domain. Many researchers succeeded to solve many challenging and diverse problems involving discontinuities using peridynamics especially after the publication of successive papers by Silling and Askari [2] and Macek and Silling [3]. The former concentrated on numerical implementation part of the bond-based PD theory and the latter is its demonstration by using commercial FE software, Abaqus.

Following the introduction of most general forms of PD theory by Silling et al. [4], which are so called ordinary and non-ordinary state-based theories, the interest on PD theory has been dramatically increased, since the limitation on material constants was removed and it paved the way of modeling more challenging problems such as plastic deformation [5]. Moreover, the application of peridynamics has also been extended to other fields such as thermal diffusion [6], electric flow [7], and hydrogen diffusion [8]. The book by Madenci and Oterkus [9] presents the numerical implementation areas of PD theory including complex laminated composite materials. Moreover, a recent book by Madenci et al. [10] brings a new aspect on solving many formidable differential equations by using PD differential operator.

The peridynamic equation of motion is usually solved by using meshless discretization methods as explained in previously mentioned publications. Emmrich and Weckner [11] compared all of the solution methods including the finite element (FE) method for a one-dimensional PD problem which does not contain any discontinuities. In that case, the FE method has the best accuracy amongst the others. However, it requires more computational time to solve the matrix equations. Besides, the meshless methods are the most convenient ones for PD problems with discontinuities. The solution does not involve any jump terms as in the CCM theory because the governing equation of PD theory is derivative-free. For this reason, most of the researchers ([3, 9]) prefer meshless midpoint rule for numerical implementation of PD theory. It is simple and easily applicable when discontinuities exist in the body. Therefore, the peridynamic equation of motion given in Eq. 2 can be written in a discrete form as

$$ \begin{array}{@{}rcl@{}} \rho(\mathbf{x}_{(i)})\ddot{\mathbf{u}}(\mathbf{x}_{(i)},\mathit{t})&=&\\ &&\sum\limits_{j=1}^{N_{(i)}}(\mathbf{t}(\mathbf{x}_{(j)}-\mathbf{x}_{(i)}, \mathbf{u}_{(j)}-\mathbf{u}_{(i)})-\mathbf{t^{\prime}}(\mathbf{x}_{(i)}-\mathbf{x}_{(j)}, \mathbf{u}_{(i)}-\mathbf{u}_{(j)}))V_{(j)}\\ &&+ \mathbf{b}(\mathbf{x_{(i)}},\mathit{t}) \end{array} $$
(3)

where Ni is the number of material points inside the horizon of the material point at x(i) and V(j) is the volume of the material point at x(j).

The most general in-house PD code mainly contains the following steps:

  • 1st step - Constructing material points: The body is composed of many small finite volumes and the center of each volume is represented by a material point located at the center of the volume. In this step, the material points are created while determining their locations in a global coordinate system.

  • 2nd step - Family member search: Family member points, which reside inside the horizon of each main material point, are determined and the family member array is created.

  • 3rd step - Surface correction: The horizon is usually truncated near the boundaries of a surface and this results in reduction of material point stiffness. Hence, the stiffness of material points near the free surfaces is corrected (see Chapter 4 of ref. [9]).For more information about different surface correction approaches available in the literature please see Le and Bobaru [13].

  • 4th step - Time integration: The PD equations are solved dynamically or statically.

When it comes to efficiency of PD codes, apart from the time integration step, the most time-consuming part is the family member search algorithm. The time consumption is very dependent on the horizon size, δ of a material point. If PD domain is going to be solved statically, the stiffness matrix must be constructed by considering family members of each material point. Stiffness matrix created in this manner will have higher density when compared with finite element (FE) implementation of CCM. Constructing such a populated global stiffness matrix can be very time consuming and this process, if not done in a most possible efficient way, can seriously impede the in-house PD code’s efficiency. Furthermore, commonly used mesh-free methods in peridynamics experience serious issues with accuracy and convergence due to rough approximation of the contribution of family nodes close to the horizon boundary [12]. This means that when creating efficient and accurate PD codes, one needs to take into account not only family search or surface corrections, but also accurate computation of volumes near the boundary of the horizon.

The family search is basically a ranged query process where the goal is to find the members which reside inside the horizon of each material point. Although it may not be always necessary, family members of a material point need to be updated if adaptive search is needed depending on the type of the problem, such as using the updated Eulerian description.

Another factor that can influence family search is the way in which surface correction factors are calculated. As explained in Le and Bobaru [13], there are several surface effect correction methods such as volume method, force density method, energy method, force normalization method, and fictitious nodes method. Most of these methods do not influence the family search process as they do not add any additional spatial data into the peridynamic model and mainly modify either the bond stiffness or the force state for bonds near the boundaries of the surface. Only exception is the fictitious nodes method where a layer of extra nodes (fictitious nodes) are added around surface boundaries so that every real node has a full horizon. In order for this approach to work, the size of the layer of fictitious nodes needs to be at least equal to one horizon size around the original PD domain. This extra layer of points will naturally increase to the number of PD points that need to be searched and increase the family search time. According to Le and Bobaru [13], although this approach practically eliminates PD surface effects, it has certain limitations especially when dealing with non-straight boundaries since family members definition becomes rapidly complex. On the other hand, peridynamic models with irregular and non-uniform discretized solution domains can also influence family search process [14]. Irregular mesh can have a large impact on gridding algorithms (Verlet list, cell-linked lists or Partitioning algorithm) as it will increase unnecessary distance computations between points.

In literature, there are few studies on family member search algorithms related with Peridynamics. Diyaroglu [15] introduced an efficient way of searching family members of each material point by utilizing localized squares for 2-dimensional (2D) and cubes for 3-dimensional (3D) configurations. Liu et al. [16] also showed a similar family search algorithm named “Family-member search with link list” which utilizes an equidistant grid of squares holding certain number of points.

On the other hand, there is an extensive body of work on near-neighbor search algorithms in molecular dynamics. Methods that are predominantly investigated are Verlet List and cell-linked list. Dominguez et al. [17] investigated the efficiency of these methods and proposed a novel neighbor search algorithm based on a dynamic updating of the Verlet List. In a study by Viccione et al. [18], numerical sensitivity analysis of Verlet List and cell-linked list efficiency was conducted. In this work, efficiency was studied as a function of Verlet List size and cell dimensions. Another interesting study was done by Howard et al. [19] where a novel approach based on linear bounding volume hierarchies (LBVHs) for near-neighbor search was introduced. In essence, bounding volume hierarchies (BVHs) are tree structures and mainly used in collision detection and ray tracing. They are very similar to R-tree structures that are investigated in this paper. Furthermore, these authors compared the LBVHs with the state-of-the-art algorithm based on stenciled cell lists and found that LBVHs outperformed the stenciled cell lists for systems with moderate or large size disparity and dilute or semi-dilute fractions of large particles (conditions typical in colloidal systems).

As a summary, peridynamics is a very attractive approach especially problems including discontinuities. Researchers are always in quest of efficient and fast codes in order to solve complex engineering problems statically or dynamically. Therefore, the main aim of this study is to compare various family member search algorithms available in the literature and propose the most convenient form for peridynamic analysis depending on the type of the problem.

2 Family Search Algorithms

The fundamental family search algorithms available in the literature from weak to robust are investigated in this section including brute-force search, region partitioning, and tree data structures.

2.1 Brute-Force Search

The most straightforward algorithm for family member search is the so-called brute-force search or exhaustive search algorithm in which all possible candidates, so-called material points, are systematically enumerated. Thus, all material points, which are active in the domain, are looped over and they are checked if they satisfy a certain criterion. The criterion in this case is whether the member material point is in the range of horizon size, δ, i.e. |x(j)−x(i)| < δ. As shown in Fig. 1, if the reference length between two material points x(i) and x(j) or the size of a bond is bigger than the specified horizon size, the material point is skipped and other points inside the domain are checked for family members of the main material point x(i).

Fig. 1
figure 1

Brute-force search algorithm for the material points, x(i)

Full size image

It is a very simple search algorithm to implement and it always determines the correct family members of a material point. Hence, all researchers without any effort can use it to solve the problems of small size, which does not consume substantial time in family search part. The computational cost is proportional to the number of candidate material points and it tends to grow very quickly as the size of the problem increases, which causes combinatorial explosion. Combinatorial explosion occurs in computing environment in the following sense: if a system has n Boolean variables, which gives two possible states (true and false), the system will have 2n possible states. If the system has n variables that can have M possible states, the system will have Mn possible states. Thus, the brute-force algorithm has the worst case complexity of O(nn), where n is the number of material points and O(.) represents amount of time to run the algorithm or so-called time complexity.

2.2 Region Partitioning

The region-partitioning algorithm proposed by Diyaroglu [15] is elaborated in this section. In this technique, the solution domain is divided into square grids as shown in Fig. 2. Instead of searching for the entire solution domain as in brute-force search algorithm, only the main grid, which keeps the main material point x and the neighboring grids, is searched for its family member points, x’. It is very easy to implement and the gain in speed is substantial compared with the basic brute search. However, the oddly shaped bodies would decrease the efficiency of this algorithm. Since the grid shapes can only be in square or cubic forms, the extra time would be spent for the points outside the main region. These points, which are outside the problem domain, must be deactivated later as shown in Fig. 2.

Fig. 2
figure 2

Material points inside the domain of interest with square grids

Full size image

Note that Mattson and Rice [20] proposed an approach similar to Diyaroglu [15] to deal with near-neighbor calculations for molecular simulation techniques such as molecular dynamics or Monte Carlo. In their work, they tried to make improvement on conventional cell-linked lists method as they divide the domain into a grid of cells populated by atoms and near-neighbor search was done over main cell and its neighboring cells. In their work, they proposed a modified cell-linked list method which should substantially decrease unnecessary internuclear distance computations (neighboring cells contain more atoms than necessary).

A rectangular problem domain with PD material points inside the square grids is shown in Fig. 3. The size of square grids, which partition the problem domain, is determined based on the size of the horizon, δ and in this example case δ = 3Δ in which Δ denotes the discretization size (distance between the material points). Region partitioning algorithm can be broken down into two sections including construction of material points and family member search parts. In the first section, each square region is constructed with 6 points along x and y directions except for the end regions. The region numbers are shown in red color. Thus, the family members of each main material point can only reside in its own and neighboring regions. The following scalars and arrays can be constructed accordingly;

  • ncl: Number of columns along x-axis

  • nrw: Number of rows along y-axis

  • lstncl: Number of points in the last column along x-axis

  • lstnrw: Number of points in the last row along y-axis

  • nrgn: Total number of regions

  • region: An array which gives the first material point’s number at each region.

For a rectangular domain shown in Fig. 3, these scalars and arrays are defined as;

  • ncl = 5, nrw = 4, lstncl = 1, lstnrw = 2, nrgn = 20

  • region (1) = 1, region (6) = 40, region (11) = 79, region (16) = 118

  • region (2) = 10, region (7) = 49, region (12) = 88, region (17) = 124

  • region (3) = 19, region (8) = 58, region (13) = 97, region (18) = 130

  • region (4) = 28, region (9) = 67, region (14) = 106, region (19) = 136

  • region (5) = 37, region (10) = 76, region (15) = 115, region (20) = 142

Fig. 3
figure 3

Partitioned rectangular problem domain

Full size image

In the second section, the family members of each main material point are determined. Thus, the following arrays can be generated;

  • nfmem: Total number of family members for each main material point

  • fmem: Family member point numbers for each main material point

  • indx: Index array which defines the main material point’s location in the fmem array

In order to create these arrays in a most efficient way and reduce the search time dramatically, the advantage of region partitioning completed in the first section is utilized. First, the main region’s number and its neighboring region’s numbers are defined and they are searched for family member points of main point. For instance, if the region 14 is chosen as the main region, the search for the family members is only performed inside the neighboring regions of 8, 9, 10, 13, 15, 18, 19, and 20. Figure 4 shows the family member material point search for the main material point 109. The regions are enumerated locally with a blue color. At this level, the following scalars/arrays can be created;

  • fpoint: The first point’s number (106) inside the main region.

  • lpoint: The last point’s number (114) inside the main region.

  • neighrw(1:9): The number of material points along x-axis at each locally numbered region;

  • neighrw(1) = 3, neighrw(4) = 3, neighrw(6) = 3, neighrw(8) = 1

  • neighrw(2) = 3, neighrw(5) = 1, neighrw(7) = 3, neighrw(9) = 3

  • neighrw(3) = 1

  • neighcl(1:9): The number of material points along y-axis at each locally numbered region;

  • neighcl(1) = 2, neighcl(4) = 3, neighcl(6) = 3, neighcl(8) = 3

  • neighcl(2) = 2, neighcl(5) = 3, neighcl(7) = 3, neighcl(9) = 3

  • neighcl(3) = 2

Fig. 4
figure 4

The neighboring regions for the material point 109

Full size image

Thus, the family members of the main material point 109 inside the main region 14 are determined. This search algorithm can further be improved by using pink colored rectangle shown in Fig. 4. The regions along x- and y-axes are numbered in the base of three as depicted in pink color. By doing so, the family member search is only allowed to be done in rectangular region with 7×7 points. Please see Appendix for family search algorithm for 3-dimensional configurations.

Although this approach gives significant amount of boost and speed in family search process, it is crude and inflexible way to organize and query the spatial data. This approach works fine for highly symmetrical meshes and straight boundaries, where the majority of the portioned regions have the optimal number of points defined by the horizon size. However, it suffers for highly irregular meshes. Furthermore, the partitioning is dependent on horizon size and any change in horizon size necessitates the repartitioning of the problem domain. These observations are self-evident when having a closer look at the algorithm, which divides the solution domain into a square grid and the family search is only done for the main region that holds the main material point and its neighboring grids. When using this approach, partitioning algorithm works on the assumption that it needs to search only the immediate neighboring grids as it expects that all the family points are contained within them. This assumption comes from the fact that the mesh has an equidistant spacing between material points which is not the case for irregular meshes. Moreover, as it was mentioned earlier, partitioning depends on the horizon size, which means that if the horizon size is changed, the partitioning needs to be updated. Updating could be done by two approaches; either number of points in each region needs to be changed or if the number of points is kept constant, then number of neighboring regions needs to be adjusted.

2.3 Tree Data Structures

The storage and queries of peridynamic points can be achieved with many data structures. The most basic data structure is a simple array. An array is a static data structure, which can be randomly accessed and it is easy to implement as in brute-force search algorithm. On the other hand, the linked-list data structures are in essence a linear collection of data elements and each element points to the next which are dynamic in nature and are ideal for frequent operations such as adding, deleting, and updating. The main drawbacks of linked-list structures compared with static arrays are the high memory consumption and the sequentially accessed data. Other data structures including stacks, queues, and hash table are specialized for complex problems.

The main disadvantage of using array or linked-list data structures to store material points is the time necessary to search for a specific point or set of points, i.e. family members. Since static arrays and linked-list structures are linear, the query time is proportional to the size of data set. This can be nicely visualized if we imagine the data set with a size of n. The number of comparisons required to find an item in the worst case scenario is O(n). Therefore, efficient data structures are needed to store and search the data.

The evolved form of linked data structure (linked-list, vector, stack, and queue) is a tree (Fig. 5), which represents collection of nodes and their relations (parent-child relationship). As compared with other linear (sequential) data structures, a tree is in non-linear or hierarchical form. A tree is either empty or comprising a root node with zero or more subtrees called children. A rooted tree form is the main interest of the current study and it has the following properties:

  • One node is distinguished as the root which is node 1.

  • Each node may have zero or more children.

  • Every node (exterior to root) is connected with directed edge from exactly one to other node and its direction is parent to children.

Fig. 5
figure 5

General concept of a tree structure

Full size image

In Fig. 5, node 1 is a parent (root node) and nodes 2, 3, and 4 are its children or subtrees. On the other hand, node 2 is a parent to nodes 5, 6, and 7. Each node can have arbitrary number of children. Nodes with no children are called leaves, or external nodes. In Fig. 5, nodes 3, 5, 7, 9, and 10 are the leaves and other nodes are called as internal nodes. Internal nodes have at least one child. Nodes with the same parent are called siblings. In Fig. 5, nodes 2, 3, and 4 are the siblings. The depth of a node is the length of the path from root to the node. For instance, the depth of node 9 is 3. The height of a node is the length of the path from node to the deepest leaf. The height of node 1 is 3. The height of a tree is equal to height of a root. The size of a node is equal to the number of nodes available in the subtree of that node (including itself). The size of node 2 is 5.

2.3.1 Binary Tree

Binary tree is a specialized case of general tree structure where each node has at most two children called the left and right child. If each node has exactly zero or two children, it is named as full binary tree. In a full tree, there are no nodes with exactly one child. A complete binary tree is completely filled from left to right with a possible exception of the bottom level. Figure 6 shows full- and complete-tree structures. A complete-tree with a height of h has between 2h and 2(h+ 1) − 1.

Fig. 6
figure 6

Two types of binary tree: a full- and b complete-tree structures

Full size image

Other types of binary tree are the balanced and unbalanced binary tree structures (Fig. 7). The height of balanced tree differs at most one from its left to the right. A balanced binary tree is also known as an AVL (Adelson Velskii Landis) tree which is developed by Adelson et al. (1962).

Fig. 7
figure 7

Balanced versus unbalanced binary tree: a balanced and b unbalanced

Full size image

2.3.2 Binary Search Trees

A Binary Search Tree (BST) is a data structure which can be traversed/searched according to an order. A binary tree is actually a binary search tree (BST) if and only if it is in an ordered sequence. The idea of a BST is the data stored in an order so that it can be retrieved very efficiently. The nodes can be sorted as shown in (Fig. 8) and in the following way:

  • Each node contains one unique key (value used to compare nodes—in case of PD this would be x,y, z position).

  • The keys in the left subtree are less than the key in its parent node (L subtree).

  • The keys in the right subtree are greater than the key in its parent node (R subtree).

  • Duplicating node keys are not allowed.

Fig. 8
figure 8

Binary Search Tree (BST) with left and right subtrees

Full size image

If BST is built in a balanced form, log time access is required for each element. In other words, algorithm needs to do at worst \(\log _{2}(\mathit {n})\) comparisons in order to find a specific node. An arbitrary BST with a height of h has total possible number of nodes equal to 2h+ 1 − 1. In order to find a particular node only one comparison needs to be performed at each level, or a maximum of h+ 1 in total. This is because each node can only have two children and only one of them satisfies the search condition. If the number of nodes, n in a tree is known, the number of comparisons to fully traverse the tree can be calculated as

$$ 2^{\mathit{h}+1}-1 = \mathit{n} $$

which leads to

$$ \mathit{h} = \log_{2}(\mathit{n})-1=\mathit{O}(\log_{2}(\mathit{n})) $$

Thus, a balanced binary search tree with n nodes has a maximum order of \(\log _{2}(\mathit {n})\) levels meaning that at most \(\log _{2}(\mathit {n})\) comparisons are needed to find a particular node. The main problem of achieving \(\mathit {O}(\log _{2}(\mathit {n}))\) is the necessity of balanced-tree form and it is not a trivial task. One of the ways to achieve the balanced-tree form is to distribute the data randomly. The probability of forming balanced-tree structure would be high. However, if the data has already a pattern (sorted list of peridynamic points), a simple FIFO (first in first out) insertion into a binary search tree will result in growing tree either to the right or to the left side of the root node. This kind of unbalanced binary search tree is no more efficient than the regular linked-list. To this end, a great care needs to be taken in order to keep the tree as balanced as possible. There are many techniques for balancing tree structures as given in refs. [21] and [22].

2.3.3 Spatial Search Trees

Spatial data or geospatial data is the information of a physical object which can be represented with numerical values in a geographic coordinate system. In peridynamic sense, this corresponds to material points with their volumes and positions in a coordinate system. The Geographic Information Systems (GIS) or other specialized software applications can be used to access, visualize, manipulate, and analyze geospatial data.

Spatial data has two fundamental query types: nearest neighbors and range queries. Both serve as a building block for many geometric and GIS problems. Solving both problems (big data problems within a realistic time span) at a scale requires defining a spatial index. Spatial indices are used to optimize the spatial queries. Conventional index types (binary search tree) do not efficiently handle the spatial queries; for instance, the query of the distance between two material points if they reside within the spatial area of interest. Some of the efficient spatial index methods such as R-tree and K-d tree searches can overcome this deficiency.

Data changes are usually less frequent than the queries, which means that incurring an initial time cost of processing data into an index is a fair price to pay for instant searches afterwards. This is especially true for most of the PD simulations in which initial family members do not change during the analysis.

Almost all spatial data structures share the same principle to enable efficient search; branch and bound. This means arranging data in a tree-like structure and discarding branches if they do not fit our search criteria. The well-known spatial trees are R-tree and K-d tree. R-tree has tree data structures used for spatial access methods as proposed by Antonin Guttman [23]. The R-tree access method organizes any-dimensional data in a tree-shaped structure called an R-tree index. The index uses a bounding box which is in a rectilinear shape such that it contains the bounded objects (in case of PDs, the objects are the material points). Bounding boxes can enclose the data objects or other bounding boxes. In Fig. 9, an R-tree with two levels of bounding boxes is shown. There are nine red boxes at the upper level and each red bounding box contains nine purple bounding boxes as the lower level. Grey points represent the peridynamic points sorted into this R-tree.

Fig. 9
figure 9

First two levels of R-tree

Full size image

On the other hand, Bentley [24] introduced K-d tree which is similar to R-tree. In this method, the points are sorted into two halves (around a median point) either left and right, or top and bottom, alternating between x and y, or x, y, and z or any other n-dimensions split at each level. Figure 10 shows the two initial splits with a red line along x-axis and subsequent splits along y-axis depicted as purple line.

Fig. 10
figure 10

First two levels of K-d tree

Full size image

Compared with R-tree, K-d tree search usually only contains points (not the rectangles) and it cannot handle the adding and removing points. However, it is easier to implement and it is usually very fast. Both R-tree and K-d tree searches share the principle of partitioning data into axis-aligned tree nodes. Since PD mesh is defined with material points which are in essence spatial data, selection of K-d or R- trees represents a logical choice when it comes to family search. In following sections, in-depth reviews of K-d tree and R-tree algorithms developed in BOOST libraries are provided and their implementation to PD codes are demonstrated.

2.3.4 R-Tree Search

R-tree is a hierarchical data structure based on B+ tree. B+ tree is a binary tree but the parent node can have more than two child nodes. R-tree is used for dynamic organization of a set of d-dimensional geometric objects (PD points can either be in 2-dimensional or 3-dimensional forms) and they can be represented by minimum bounding d-dimensional rectangles (MBRs). Each node of R-tree corresponds to the MBR that bounds its children.

It must be pointed out that the MBRs surrounding different nodes may overlap with each other. Furthermore, MBR can include (in a geometrical sense) many nodes, but it can be associated only one of them. This means that a spatial search may visit many nodes before confirming the existence of a given MBR. This also can lead to false alarms when representing geometric object with their MBRs. To avoid these kinds of mistakes, the candidate objects must be examined. For example, Fig. 11 illustrates the case where two peridynamic material points and their horizons (red circles) which are not intersecting but their MBRs do. Therefore, R-tree represents a filtering mechanism for reduction of extremely costly direct examination of geometric objects.

Fig. 11
figure 11

Intersecting MBRs, where peridynamic family member points are only in MBR A

Full size image

An R-tree is defined by its order (n, N) and it has the following characteristics:

  • Each leaf node (unless it is the root) can host up to N entries (peridynamic points), whereas the minimum allowed number of entries is n ≤ N/2. Each entry has the form of (mbrID, oID), where mbrID represents the identifier of MBR that spatially contains the object and oID is the object’s identifier (peridynamic point).

  • Each internal node can store between n ≤ N/2 and N entries (MBRs). Each entry is of the form (mbrID, p), where p is a pointer to the child of the node and mbrID is the MBR that spatially contains the MBRs contained by child p.

  • The minimum allowed number of entries in the root node is 2, unless it is a leaf. When the node is a leaf, it can contain zero or single entry because leaf nodes represent the end of a tree.

  • All leaves of the R-tree are at the same level.

R-tree is a height-balanced tree with all leaves are at the same level. Since, R-trees are dynamic data structures, the global re-organization does not require to handle insertions or deletions. It is one of the main advantages of R-tree compared with K-d tree and AVL tree. Figure 12 shows a set of MBRs with some data geometric objects. This can represent PD points. The MBRs are from number 1 to 32 and they are stored at the leaf level of R-tree. Five MBRs (A, B, C, D, and E) organize the aforementioned rectangles (where each contains 9 peridynamic points) into an internal node of R-tree. Assuming N = 10 and n = 5, Fig. 13 depicts corresponding MBRs.

Fig. 12
figure 12

MBR data and their inner nodes

Full size image
Fig. 13
figure 13

MBRs data and their inner nodes

Full size image

2.3.5 K-d Tree Search

A K-d tree, or k-dimensional tree, is a binary data structure, which stores k-dimensional data, for organizing number of points in a space with k dimensions [24]. Each level of K-d tree splits all children with specific dimension. Each level of the tree is compared against one dimension. This means that every node has 2 children each corresponding to an outcome of the comparison of two records based on a certain key which can be chosen as “discriminator.” In a similar manner with standard binary tree, the K-d tree subdivides the data at each recursive level of the tree. Unlike standard binary tree, which uses only one key for all tree levels, the K-d tree uses k keys and it cycles through these keys for every successive tree level. In order to build 2-dimensional K-d tree (2-d tree) which comprises (x, y) coordinates, the keys would be cycled as x, y, x, y and so on for all the successive levels of K-d tree [25].

Figure 14 demonstrates the working mechanism of K-d tree. An array of points is inserted (first node in the array is a root node) to the system which eventually produces unbalanced tree. The array is given as follows:

$$ \textit{Ar} = [(8,9), (5,11), (15,10), (10,7), (5,3), (2,6), (12,4), (1,7)] $$

The first cutting plane is in the x direction (blue line) and the next cutting plane is in the y direction (red line) and so on. This process is repeated until the leaf level is reached meaning that there are no more points to insert.

Fig. 14
figure 14

2-d tree

Full size image

2.3.6 Balanced K-d Tree Search

When building a K-d tree, due to the use of different keys at successive levels of the tree, it is not possible to employ rebalancing techniques.Building K-d tree data structure would cause unbalanced structures. The reason of this is the use of different keys at successive levels of tree data. Moreover, it is not possible to employ rebalancing techniques. Rebalancing techniques are used to build self-balancing AVL tree [26], where if the height of two child subtrees of any node differ by more than one. In that case, rebalancing is performed to restore the height. Another self-balancing tree is the so-called the red-black tree ([21] and [22]), where each node of the binary tree has an extra bit. This bit is often interpreted as the color (red or black) of a node. These color bits are then used to ensure that the tree remains approximately balanced during the insertions and deletions. Since it is not possible to employ rebalancing techniques, the typical approach to building a balanced K-d tree is to find the median of the data for each recursive subdivision of the data. Bentley [24] showed that if the median of n elements is found in O(n) time, it would be possible to build a depth-balanced K-d tree in \(\mathit {O}(\mathit {n}\log {(\mathit {n})})\) time. In order to find the median of n elements, sorting algorithm needs to be applied to the data. Most widely used sorting algorithms are Quicksort, Merge Sort, and Heapsort. Quicksort [27] is a divide and conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. In the best case scenario, Quicksort finds the median in \(\mathit {O}(\mathit {n}\log {(\mathit {n})})\) time and in the worst case scenario, the time increases up to O(n2). Merge Sort [28] is also a divide and conquer algorithm. The idea behind the Merge Sort is to divide the unsorted list into n sublists. Each sublist contains one element and a list of one element is considered as sorted. Afterwards, Merge Sort repeatedly merges sublists to produce a new sorted sublists until there is only one sublist remaining. On the other hand, Heap sort is a comparison-based sorting technique based on Binary Heap data structure. It is similar to selection sort which finds the maximum element. Merge sort and Heapsort find the median in the best case of \(\mathit {O}(\mathit {n}\log {\mathit {n}})\), which leads to \(\mathit {O}(\mathit {n}\log ^{2}{\mathit {n}})\) time for a balanced K-d tree [29].

An alternative approach to building a balanced K-d tree would be the presorting data prior to building a tree [25]. The algorithms developed by Brown [25] are implemented in our in-house PD solver. The PD points are presorted in each of k dimension prior to building K-d tree. Thus, it maintains the order of these k sorts when building a balanced K-d tree. This in return achieves a worst-case complexity of \(\mathit {O}(\mathit {kn}\log {\mathit {n}})\).

Basic concepts of balanced K-d tree algorithm can be explained with the following simple example. A small sample of spatial data is considered. This data can be viewed as a set of PD points from which a K-d tree is created. The data set consists of 15 (x, y, z) tuples (PD points) which are stored into a list of elements numbered from 0 through 14 as shown in Fig. 15. First step is to presort the PD points using merge sort. The points are sorted via super keys; x:y:z, y:z:x, and z:x:y which represent cyclic permutations of x, y, and z. The points are not sorted independently through x, y, and z coordinates but each part of the super key (x, y, and z) has a certain level of significance. Hence, for example, the super key y:z:x is composed from y as a primary key, z as a secondary key, and x as a tertiary key. This means that during the merge sort, if the two points have identical primary keys, then they are compared using secondary key, and if their secondary keys are identical, they are compared using the tertiary key. In case of all the three keys are the same with two identical points, one of the points is removed.

Fig. 15
figure 15

2-d tree

Full size image

In order to have initial array of points untouched and to save on memory consumption, the merge sort does not work with initial array of PD points. Instead, it reorders three index arrays whose elements point to array indices. The initial order of indices produced by merge sort is shown in (Fig. 15) (see xyz, yzx and zxy columns under “Initial Indices”). The next step is to partition the points in x direction, which is the first splitting dimension, by using x:y:z super key. There, the partition location is specified by the median element of the xyz-index array under “Initial Indices.” The partition results are shown in (Fig. 15) under “After first split” column in which the partitioning does not reorder the array of PD points. Instead, it reorders the yzx- and zxy-index arrays. Please note that xyz-index array requires no partitioning as it is already sorted in x direction and this was done when “Initial Indices” arrays were created. However, the yzx- and zxy-index arrays require partitioning in x direction by using the x:y:z super key defined by median point 7:2:6. The partitioning of yzx index array is achieved as follows:

  1. 1.

    The elements of yzx-index array are compared with super key (median element of index array—7:2:6)

  2. 2.

    They are copied either in upper half if they are less than the x value or in lower half if they are bigger than the x value from xyz super key.

  3. 3.

    The same procedure is repeated for zxy-index array.

The columns of “After First Split” reveal that the index value of 5 is absent from the index arrays since it represents the partitioning value. It also becomes the root of nascent K-d tree, as shown in Fig. 16. The same procedure is also repeated for y direction, and the partitioned values (see column “After Second Split” in Fig. 15) are removed and stored as children nodes of the root node. This recursive process is repeated until index array consists of only one, two, or three elements. In the case of only one point is left after the final split, it is automatically stored as a new node of K-d tree. If there are two or three points left, these points are already sorted in the index array. So, the determination of which point referencing a new node and which point referencing from children is trivial.

Fig. 16
figure 16

A K-d tree built from (x, y, z) tuples

Full size image

2.3.7 Boost R-Tree Algorithm

R-tree is currently the only spatial index implemented in “Boost.Geometry.Index” library which is a part of overall Boost library [30]. The intended use of “Boost.Geometry.Index” is to gather data structures defined as spatial indexes which can be used to accelerate searching for objects in multidimensional spaces. In general, spatial indexes store representations of geometric objects which allows the end user to search for objects occupying some space or object close to some point in a space.

R-tree is a tree data structure used for spatial queries and it is first proposed by Antonin Guttman [23]. Since all objects lie within a bounding rectangle, a query, that does not intersect the bounding rectangle, also cannot intersect any of the objects contained in the bounding rectangle. Similar to B-tree, R-tree is also a self-balanced search tree. The key part of balancing algorithm is the node splitting algorithm ([31] and [32]). Each algorithm produces different splits such that the internal structure of a tree may become different for each one of them. This means that more complex algorithms can better analyze the elements and produce less overlapping nodes. The tree with less overlapping nodes is more efficient in a search process because less nodes must be traversed in order to find desired objects. The downside of higher complexity algorithms is that analysis takes more time. In general, faster inserting results in slower querying and vice versa. Performance of R-tree is contingent on balancing algorithm, parameters, and the data inserted into a container.

Most trees with searching algorithms (e.g., intersection, spatial search, nearest neighbor search) are rather simple. The key idea is to use the bounding boxes to decide whether or not to search inside a subtree. This means that most of the nodes in a tree are traversed during the search. R-trees are suitable for large data sets and databases, where the nodes can be paged to memory as needed and the whole tree cannot be kept in the main memory.

Table 1 Example structures of trees created by different algorithms and their operations times
Full size table

The main problem with an R-tree is that the rectangles do not encompass too much empty space and do not overlap too much (fewer subtrees need to be processed during the search). On the other hand, they are balanced (leaf nodes have the same height). Most of the research and improvements of R-trees are aimed at improving the tree building process and they are defined by two main objectives: 1—Building an efficient tree from scratch (bulk-loading) and 2—Performing changes on an existing tree (insertion and deletion). Boost R-tree implements several building algorithms which are linear algorithm, quadratic algorithm, R*-tree algorithm, and packing algorithm (bulk loading algorithm). As can be seen from Table 1, packing algorithm is faster when building the R-tree and also R-trees with better internal structure gives faster spatial and k nearest neighbors (knn) queries.

3 Comparative Performance of Search Algorithms

In order to compare performance between brute-force search algorithm, region partitioning search algorithm, balanced K-d tree, and boost R-tree with packing algorithm, several example cases were considered. Multiple cubic 3-dimensional PD meshes were created, ranging from 27000 to 8000000 points. Maximum number of family points for the 3D mesh with a horizon of 3Δ is 122. The configuration of the machine used for testing is Intel(R) Core(TM) i7-4510U @ 2.0GHz, 8GB RAM, MS Windows 10 x64. In Table 2, timings for family search are presented. Figure 17 presents the data from Table 2 except the brute-force search since those times are not comparable with the rest of the algorithms. In Table 3 and Fig. 19, times for building the K-d&R-tree structure are shown. Because the brute-force and region partitioning algorithm do not require any specific structure except for an array of points, there was no need to include them in Table 3 and Fig. 19.

Fig. 17
figure 17

Time comparison for different family search algorithms

Full size image
Table 2 Family search time comparison
Full size table

As it can be seen from Table 2, brute search is the worst performing algorithm as it would be expected. This should indicate that the brute search algorithm should only be used when doing initial testing of the PD algorithm on relatively small mesh and not as a strategy for complex problems. Comparing the rest of the algorithms, it can be seen that region partitioning search algorithm performed best. This is further supported when different horizon sizes are used as it can be seen from Fig. 18 where all tree algorithms are tested for two different horizon sizes H = 3Δ and 6Δ. Number of family points for horizon sizes 3Δ and 6Δ is 122 and 924, respectively. All of these benefits come with several caveats. First of all, this algorithm is not scalable. As it can be seen from Table 2, both R and K-d trees have more or less linear increase of family search time between 1,000,000 and 8,000,000 points but region partitioning algorithm does not. Moreover, region partitioning algorithm is built to fit a specific purpose, which is family search of very regular meshes, preferably rectangular or cubic shaped. Secondly, all of the arrays are either statically allocated or dynamically allocated, but with a purely defined sizes; for example in region partitioning algorithm size of the family members array for a 3-dimensional configuration and horizon size of 3Δ is defined as number of points ×150 (max size of family members for one point is 122 for this specific horizon). Although this can be easily changed, we would still allocate more memory space than necessary as not all points will have max number of family points (points close to edges of the mesh). Thirdly, if the horizon size changes or horizon shape is not a circle/sphere, user would need to thoroughly rewrite the algorithm which is not easy as the code itself is very complex. This algorithm could be used also for initial testing of the PD algorithm that would require large but symmetrical meshes where use of third party libraries is not possible.

Fig. 18
figure 18

Time comparison for different horizon sizes H = nΔ for 1000000 points

Full size image
Table 3 Times necessary for building the tree structure
Full size table

Comparing balanced K-d tree to the boost R-tree with packing algorithm, it is obvious from the timings that boost R-tree performs better. R-tree performs better in building the tree structure and family search (Table 3 and Fig. 19). Furthermore, one of the problems with balanced K-d tree is relatively high memory consumption when building the tree structure, compared with the boost R-tree. The reason behind this is the need for constant sorting of points after each split in order to keep the tree balanced. This makes boost R-tree more memory friendly for extremely large meshes. Moreover, with the boost R-tree, it is easy to change the shape of the horizon as the user can overload the geometry definition of the bounding box with different shapes when doing spatial queries. Only possible negative side for the boost R-tree is dependence on third party development and maintenance of the necessary libraries. In conclusion, boost R-tree seems currently the best option if there is a need for highly scalable, relatively fast, and versatile spatial query algorithm.

Fig. 19
figure 19

Time comparison for building the tree structure between balanced K-d tree and boost R-tree with packing algorithm

Full size image

4 Conclusion

In this study, four different family search algorithms were considered including brute-force search, region partitioning search, balanced K-d tree, and boost R-tree with packing algorithm. By varying the number of material points inside the solution domain, computational time spent for family member search was determined. According to the results, brute-force search is the worst performing algorithm and it should be used for small number of material points and testing purposes. Although region partitioning search algorithm performed very well, it is limited to large and symmetrical meshes. Finally, it was concluded that boost R-tree is the best option amongst all four different algorithms considered in this study.